求解粘弹性问题的时域自适应等几何比例边界有限元法
2020-02-10何宜谦王霄腾祝雪峰杨海天薛齐文
何宜谦,王霄腾,祝雪峰,杨海天,薛齐文
(1.大连理工大学工程力学系/工业装备结构分析国家重点实验室,辽宁,大连 116024;2.大连理工大学汽车工程学院,辽宁,大连 116024;3.大连交通大学土木工程学院,辽宁,大连 116028)
许多材料具有粘弹性性质,如混凝土、高聚物、沥青、陶瓷、生物组织等,粘弹性问题的求解具有重要的工程背景和理论探讨价值[1-4]。由于时间相关的本构关系,加之复杂的边界形状/边界条件,粘弹性问题通常难以解析求解,因此,发展准确有效的数值方法十分必要。
对时空耦合的粘弹性问题的数值求解,需同时考虑时间和空间的离散计算及计算精度。基于分段积分/差分的时域粘弹性问题数值求解方法[5-8],当积分/差分阶数较低,计算精度受时间步长大小影响较大,而恰当的步长大小往往是预先难以确定的。基于积分变换与对应性原理的数值方法[9-12],通常需要进行数值的积分逆变换,其间可能产生的计算误差将影响到时域的计算结果。
另一方面,可在有限元方法[13]、无网格方法[14]、边界元方法[15]等求解粘弹性问题的基础上,发展新的数值方法,以进一步提高粘弹性问题的空间数值求解精度。
等几何分析[16](isogeometric analysis, IGA)基于有限元分析方法的等参单元思想,将计算机辅助几何设计(CAGD)中用于表达几何模型的非均匀有理B样条(NURBS)的基函数作为场函数的形函数。由于NURBS基函数具有高阶连续性,可精确描述各种几何,因此基于NURBS的IGA具有良好的计算精度和收敛性[17],并实现了CAD与CAE的无缝结合。
将等几何分析技术用于粘弹性问题的求解,有望利用等几何分析的以上优点,以进一步提高粘弹性问题的空间数值求解精度。但目前有关IGA在粘弹性数值求解中应用的文献报道鲜有涉及。Erfan等[18]结合 IGA有限元和时域差分方法建立了一个粘弹性振动问题的数值计算模型,但限于一维问题且时域采用一阶差分格式。
比例边界有限元法(scaled boundary finite element method, SBFEM)是一种半解析的边界类的数值方法[19],适于处理无限域和应力奇异性问题,并已在粘弹性问题的数值求解中得到应用[20]。
林皋、宋崇民、刘俊、王文渊等将IGA和SBFEM相结合,建立了IG-SBFEM模型,并应用于静力学、动力学、电磁场、结构地基相互作用、热传导、液体晃荡等问题的求解[21-28]。但目前似尚未见到IG-SBFEM求解粘弹性问题的直接相关报道。
时域分段自适应算法是一种求解时空耦合问题的时域高精度数值算法,已与有限元、边界元、无网格等空间数值方法相结合,用于瞬态热传导、动力学和粘弹性等问题的数值求解[29-30]。该算法的主要特点是可将一个时空耦合转化为一系列具有递推格式的空间问题,可在每个时间段内通过自适应计算,保证对不同时间步长保持稳定的计算精度。
基于以上考虑,本文将时域自适应算法和等几何比例边界元法(IG-SBFEM)相结合,提出了一种新的求解粘弹性问题的数值方法。利用时域分段自适应算法将粘弹性问题解耦,建立了递推格式的IG-SBFEM计算模型,并采用自适应技术递推求解,并将求解结果与解析解和参考解进行了比对。
本文算法在时域通过分段时域自适应计算,保证不同时间步长的计算精度;在空间具有径向解析性,且可对几何模型进行更精确描述。
论文章节安排如下:第1部分和第2部分分别推导了基于时域分段展开的粘弹性递推控制方程和本构方程,第3部分推导了IG-SBFEM的求解格式,第4部分给出了三个算例验证,第5部分为结论。
1 递推控制方程
粘弹性问题的控制方程为:
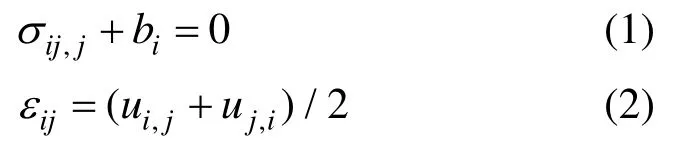
边界条件为:
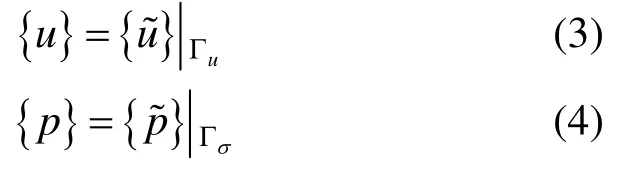
将时域划分为若干离散的时间段,在各离散时段内,将各变量展开为:


式中,tk_1和Tk分别表示第k段时间间隔的起始点和大小。
导数的转换关系可为:

将式(5)~式(12)代入式(1)~式(4)中,原初边值问题式(1)~式(4)转化为以下具有递推形式的边值问题:
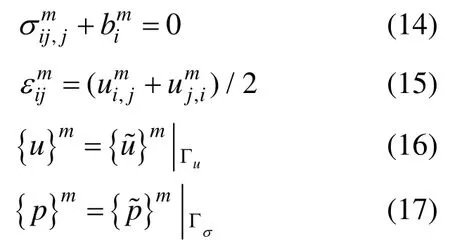
2 递推本构方程
考虑图1所示的三参数固体粘弹性模型,其微分本构关系为:
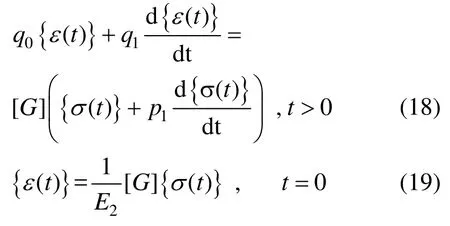
其中:
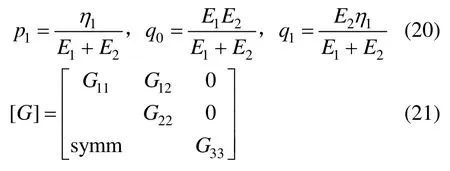
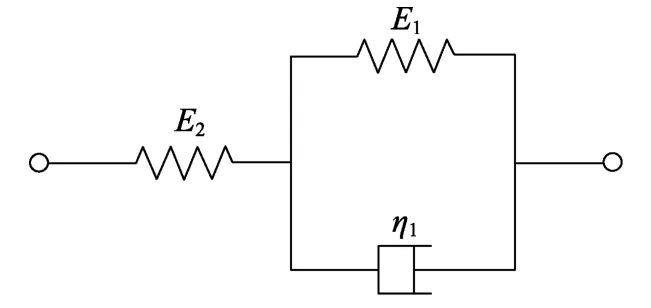
图1 三参数固体模型Fig.1 Three-parameter solid model
对于平面应力问题:
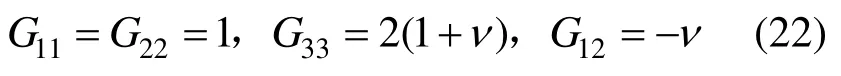
对于平面应变问题:
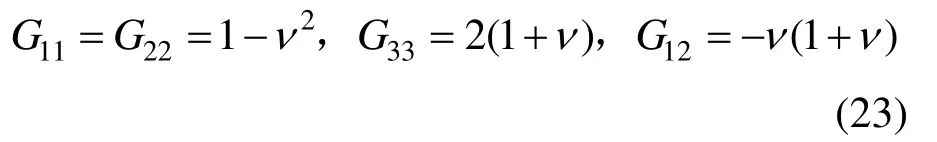
将式(5)~式(6)和式(13)代入式(18),并比较等式两边同次幂数的系数:
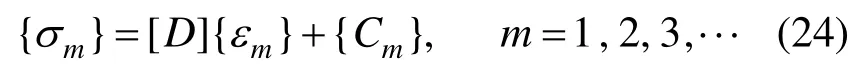
其中:
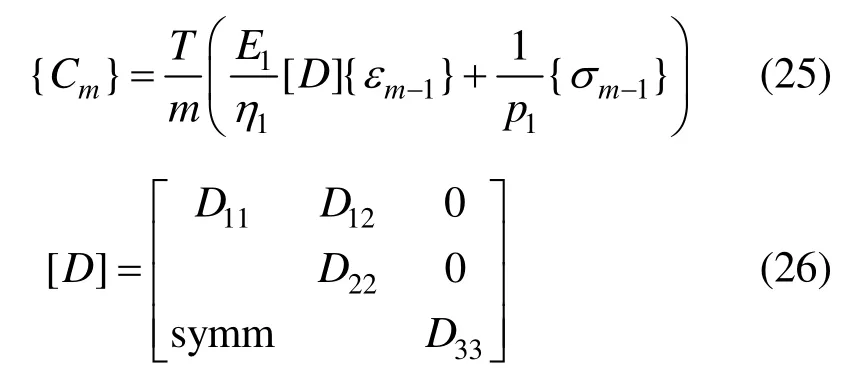
对于平面应力问题:
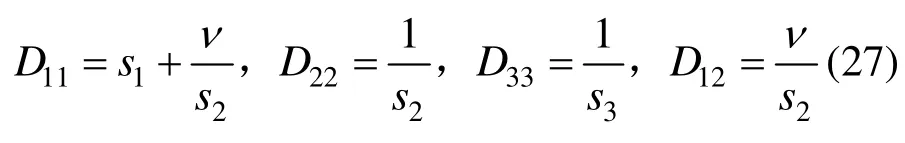
其中:

对于平面应变问题,需要将E1、E2和v分别替换成
在第一时段:

在第(k+1)时段:
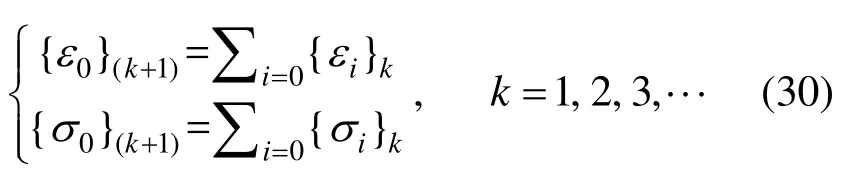
其中,下标(k+1)和k分别表示第(k+1)和第k次时间间隔。
3 递推IG-SBFEM方程
3.1 NURBS基函数
NURBS是对B样条进行有理化构造后得到的有理样条函数。在一维参数坐标空间中选定一组节点,记作设n为基函数个数,p为基函数最高次数。
一维B样条基函数的递推关系定义为:
当p=0时,
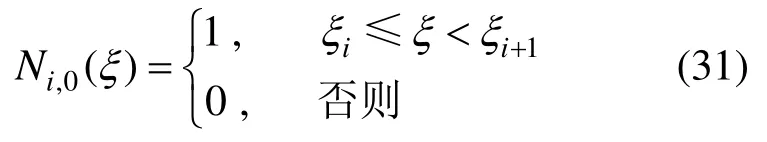
当p≥1时,
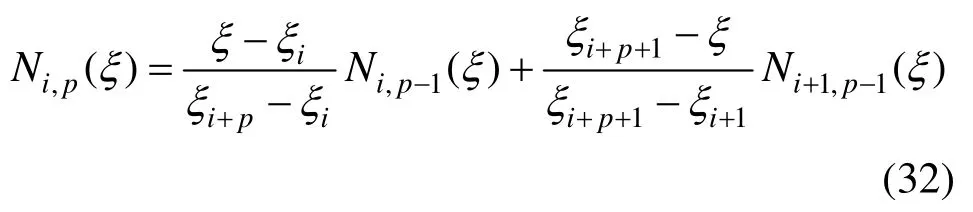
通过引入权参数对 B样条进行有理化,得到NURBS基函数:
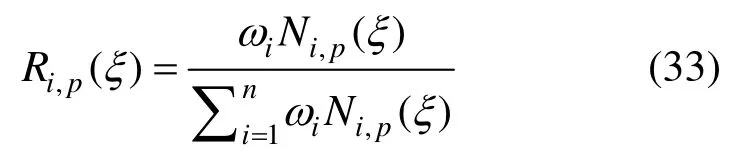
式中,为对应的权参数。
利用下式,任意形状曲线均可由NURBS基函数和控制点坐标精确表示:
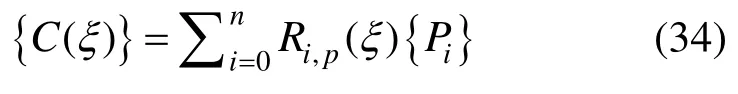
3.2 递推IG-SBFEM求解格式
采用如图2所示的比例边界坐标系,其中径向坐标ƞ比例中心处ƞ=0,在边界处ƞ=1。环向坐标表示曲线到起始点的距离,比例边界坐标系与笛卡尔坐标系的转换关系如下:
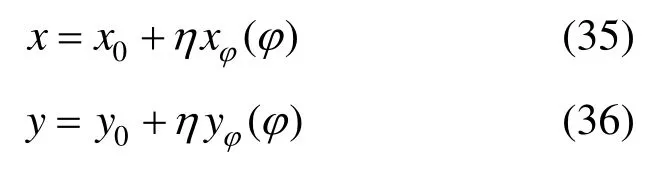
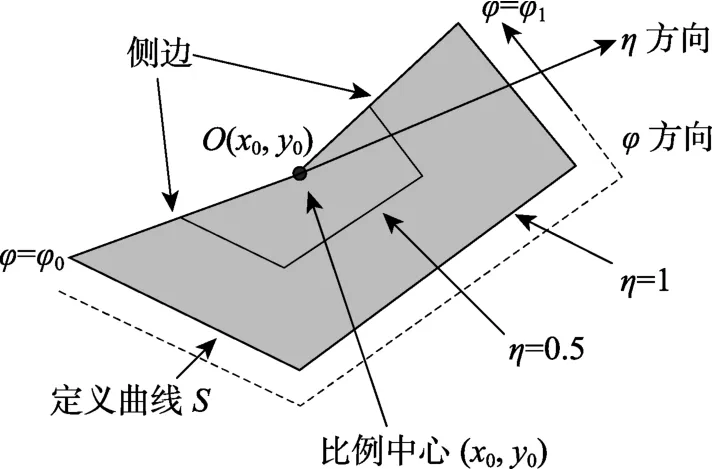
图2 比例边界坐标系Fig.2 Scaled boundary coordinate system
对于一个SBFEM建模的子域边界,在环向采用NURBS离散,节点向量为任一点坐标表示为[22]:
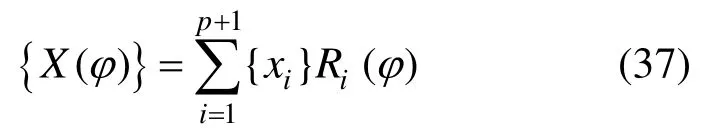
在比例坐标系统中:
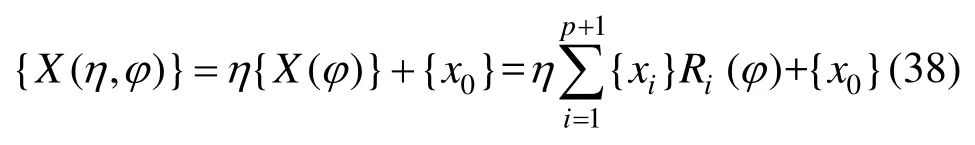
对位移采用NURBS基函数离散,得到:
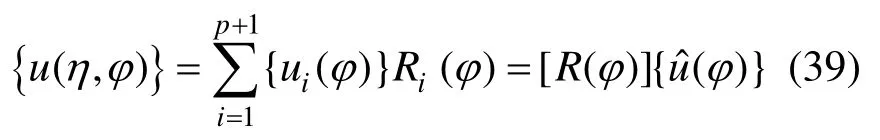
比例边界坐标系中的应变算子为[31]:
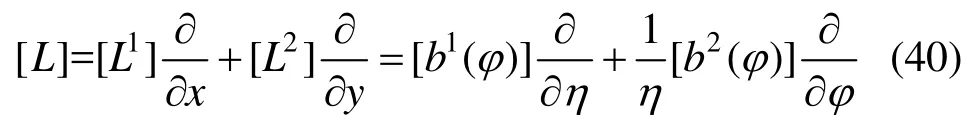
在无体力的情况下,由虚功原理可得:
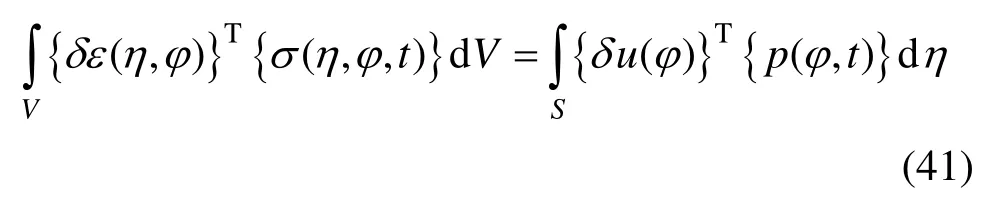
将式(24)代入式(41)可得:
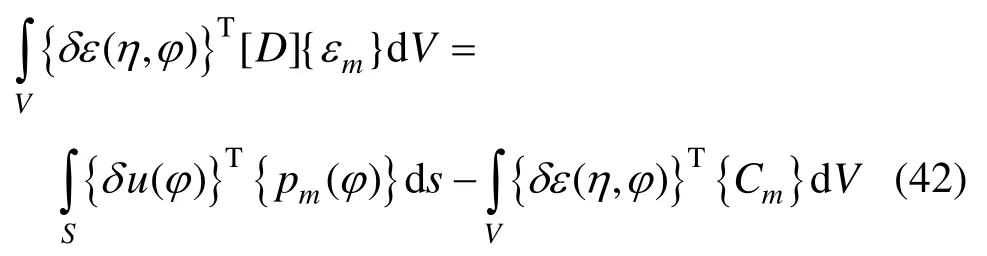
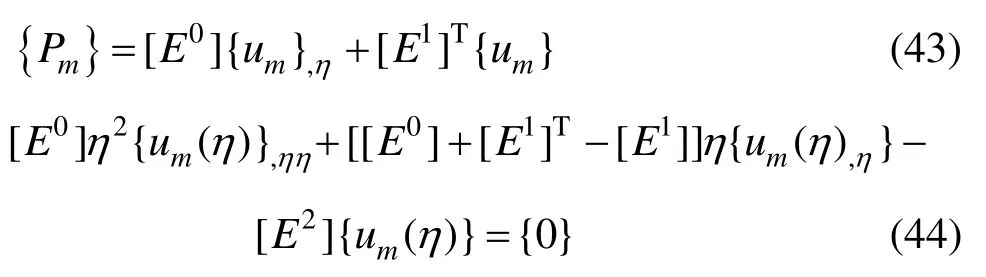
其中:
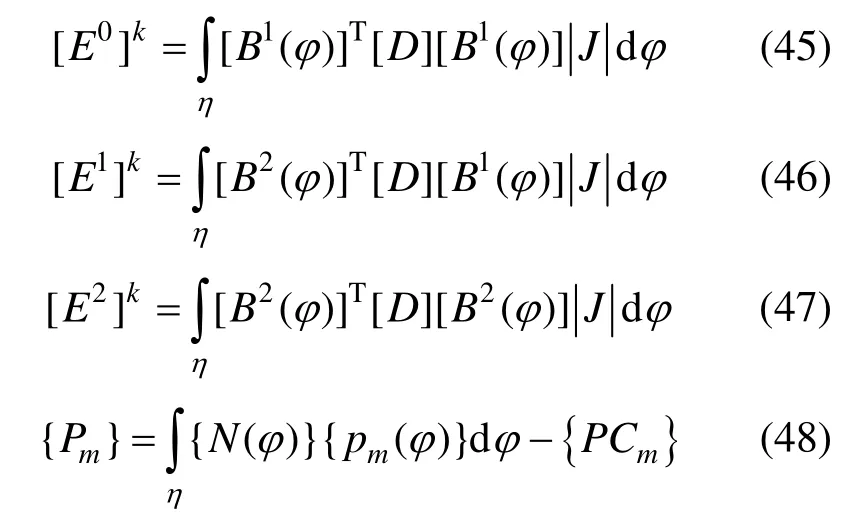
其中:
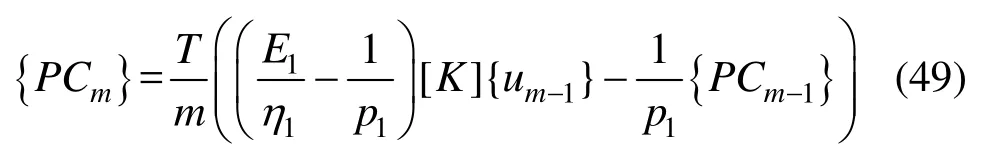
式(42)~式(43)的解为[31]:
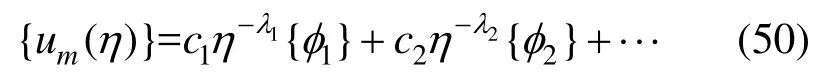
将式(50)代入式(42)、式(43)可得:
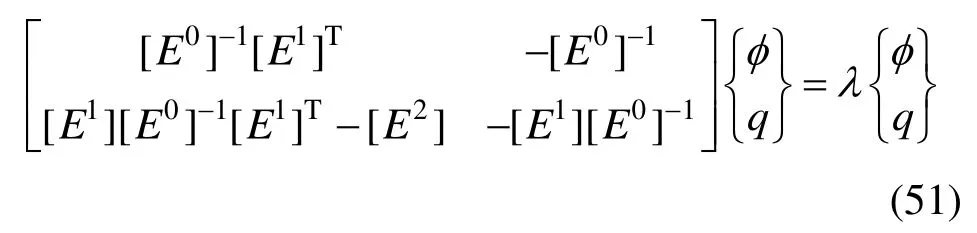
求解以上的特征值方程,可得到求解域的刚度矩阵为:
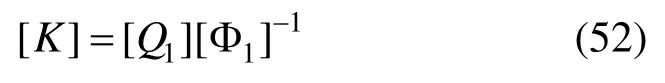
式中:[φ1]由n个特征向量组成;[Q1]由特征向量{q}组成[31]。
因此,边界节点位移向量的m阶求解方程为:

在第k个时段起点,
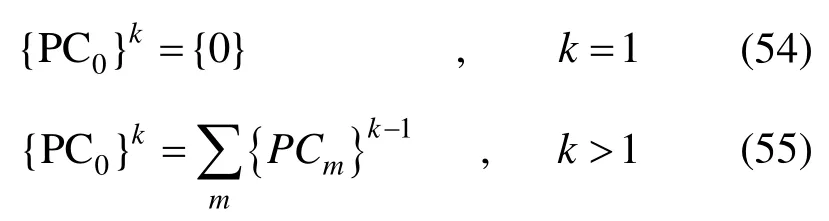
在各时间内的收敛准则为:
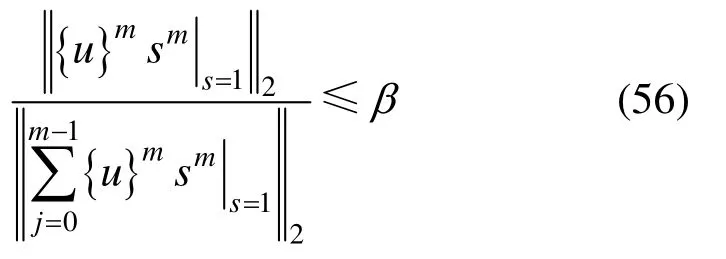
式中:β是规定的误差限;表示L2-范数。
由于 NURBS边界单元的控制点不具有插值性,本文采用一种利用NURBS基函数的单位分解性施加本质边界条件的方法[23],对于常位移边界条件,将与边界相关的控制点分成两组,在上恒为零的和不恒为零的有:
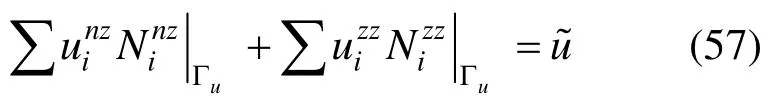
对式(57)的非负基函数项利用 NURBS基函数的单位分解性,将求解域上的边界约束条件转化到控制点上:

与上式相对应的递推边界条件为:

4 数值算例
4.1 半无限域蠕变问题
考虑一个受单向拉伸的带圆孔的粘弹性无限域,受x方向的体力f= 100 N/m2,利用对称性取如图3所示的1/4区域分析,位移边界条件如图3所示。粘弹性材料本构采用三参数固体模型,并采用岩体材料参数E1=1 960N/m2,E2=9 800 N/m2,ƞ1=5 2083(Pa·d)/m2[20]。
考虑到本文算法将时间相关的粘弹性问题转化为一系列弹性问题求解如式(53)所示,因此,本文算法的计算精度依赖于弹性问题的IG-SBFEM计算精度。以文献[32]中式(44)的能量误差范数ƞE为指标,将IG-SBFEM计算结果与文献[32]的计算结果相比较,计算结果如图4所示,对于本算例,在相同的自由度情况下,IG-SBFEM比线性和二次的SBFEM具有更高的计算精度。
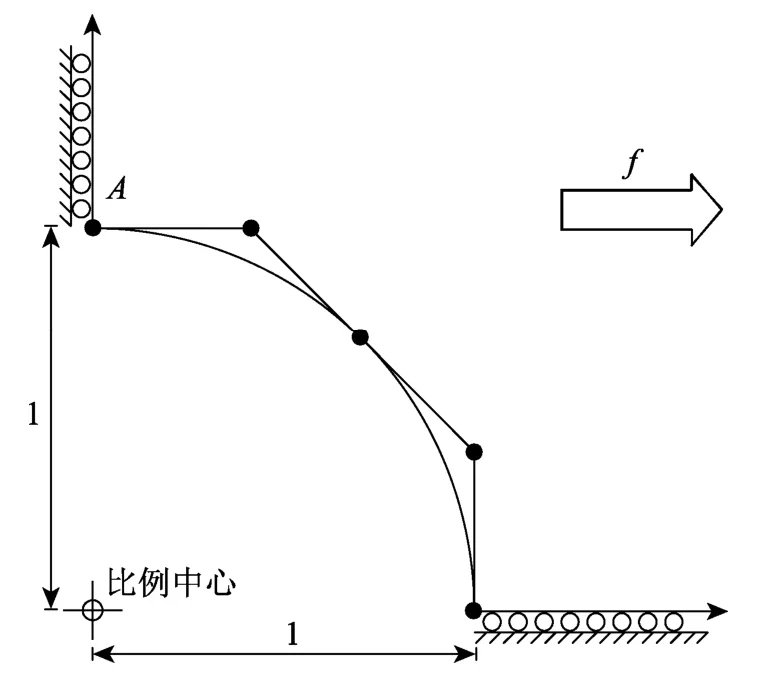
图3 带有1/4圆孔的半无限长粘弹性体区域Fig.3 A semi-unbounded viscoelastic plate with 1/4 circular hole
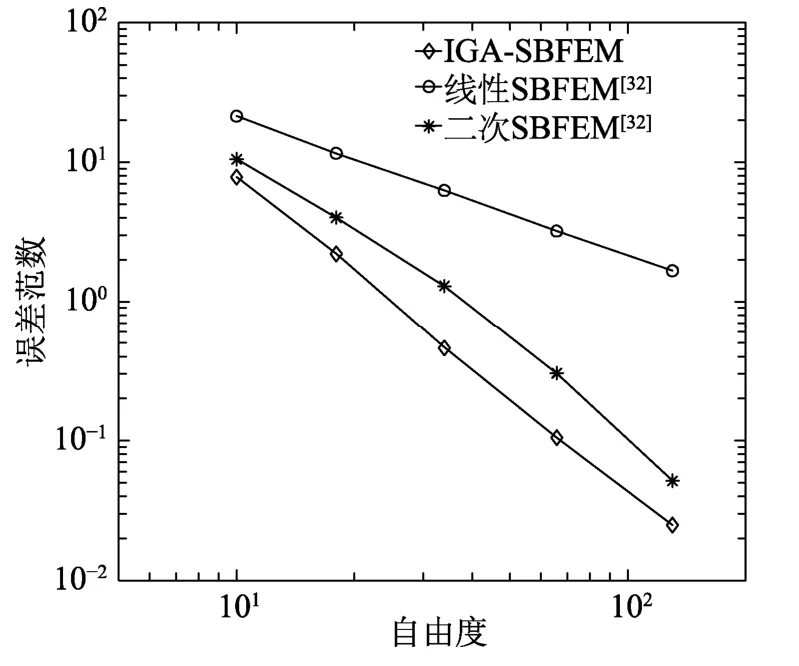
图4 应力误差范数随自由度的变化曲线Fig.4 The variation of stress error norm with DOF
图5给出了点A的蠕变曲线,分别采用线性和二次SBFEM和IG-SBFEM进行计算,参考解由二次SBFEM得到的收敛解提供[32]。IG-SBFEM采用5个控制点,常规线性和二次SBFEM使用5个节点。计算结果显示,在相同节点情况下,IG-SBFEM计算得到的蠕变曲线更加接近参考解。
采用相对偏差范数评估计算精度[33]:
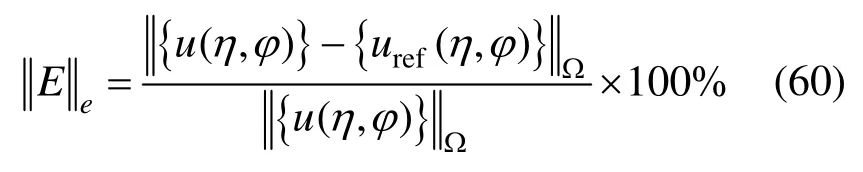
其中:
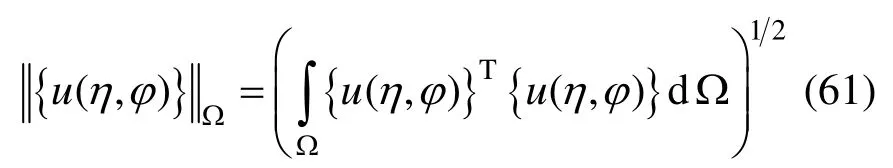
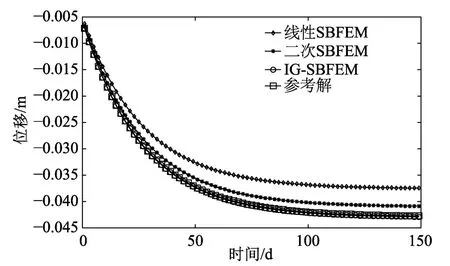
图5 A点蠕变曲线Fig.5 Creep curve of point A
图6(a)和图6(b)通过A点在不同时刻的位移解,比较了SBFEM与IG-SBFEM在不同自由度下的考虑1<ƞ<3区域内的偏差范数曲线,采用平均斜率计算收敛阶次mc。计算结果显示,IG-SBFEM具有更高的计算精度和更快的收敛性。
图6(c)比较了SBFEM与IG-SBFEM在三种自由度下的计算时间,结果显示,在相同自由度下,IG-SBFEM和SBFME的计算耗时相差不大。
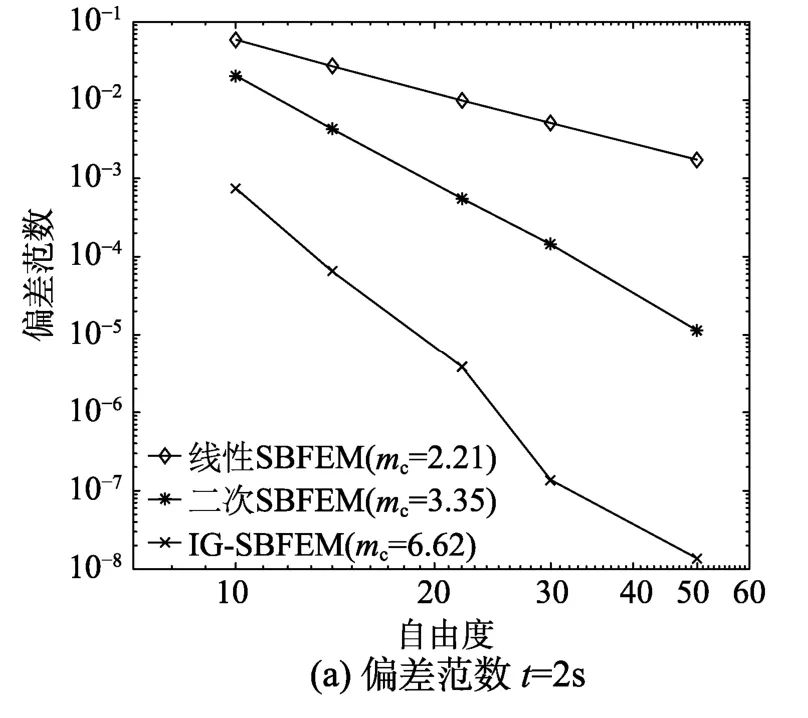
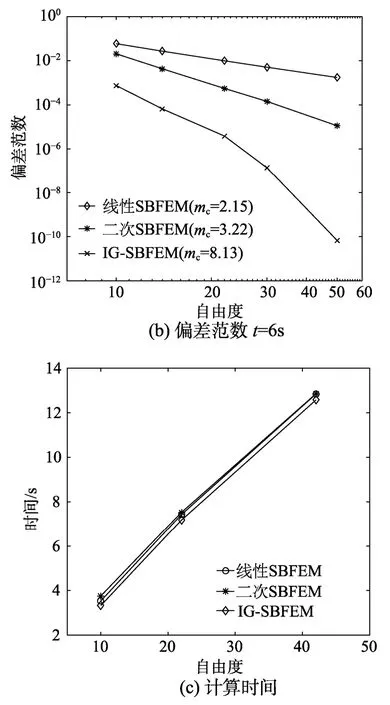
图6 偏差范数和计算时间随自由度的变化曲线Fig.6 The variation curve of the error norm and computation time with DOF
表1给出了点A在不同时刻的位移解,在相同控制点/节点情况下,IG-SBFEM计算结果的最大偏差仅为0.5068%,而二次SBFEM和线性SBFEM的最大偏差分别为1.6312%和5.5051%。
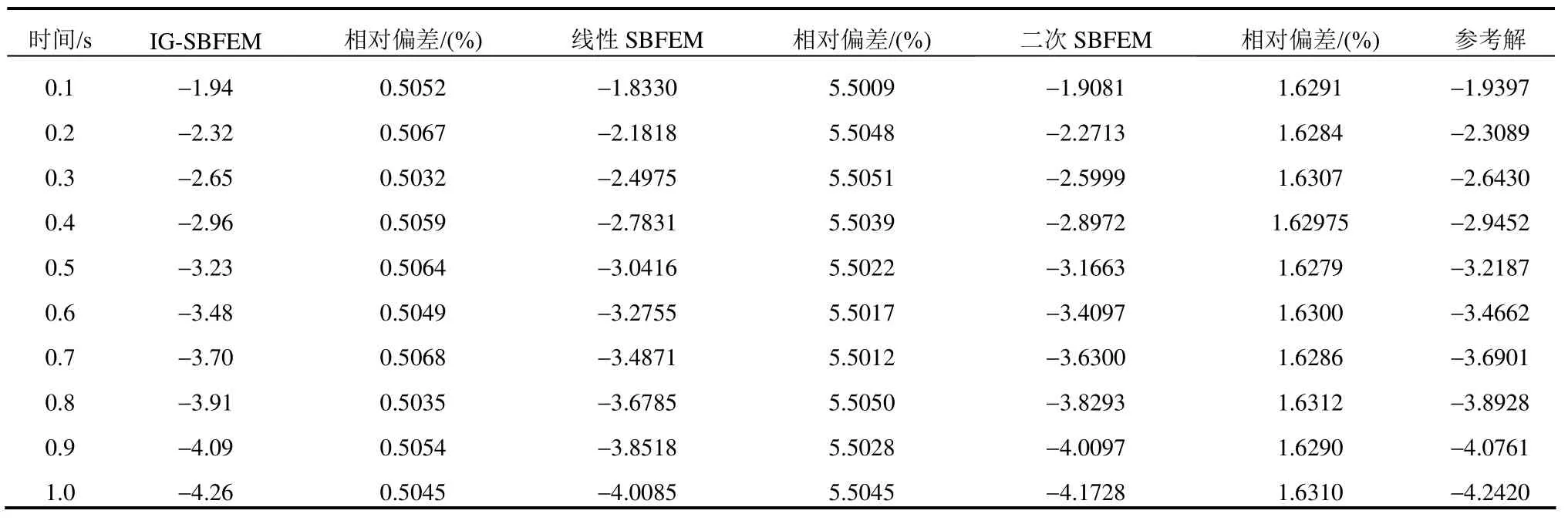
表1 位移数值解与参考解的比较Table 1 Comparison of numerical solutions and reference solution for displacement
图7通过A点的位移解,描述了误差限β对展开阶次的影响。计算结果显示,与相比,的误差限需要更多的展开阶数,可见所提方法可根据不同的精度要求自适应地调整展开阶数。
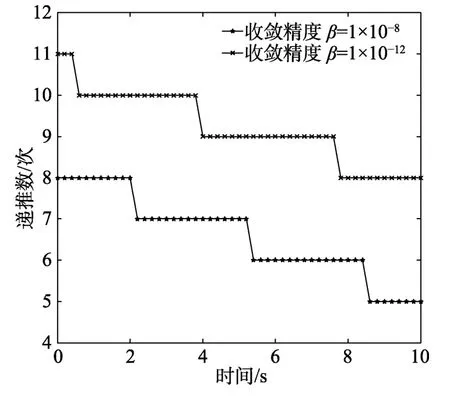
图7 展开阶次随时间的变化Fig.7 The variation of expansion order with time
4.2 带裂纹粘弹性平板的应力松弛问题
考虑一个裂纹的粘弹性平板,如图8(a)所示,h=b=1 m ,c=0.15m ,平板上侧施加常位移边界条件u0=5×10-4m ,粘弹性材料本构采用三参数固体模型,并采用混凝土材料参数E1=1 9600 N/m2,E2=1 9600N/m2,ƞ1=6 35420(Pa·d)/m2[17]。IG-SBFEM数值模型如图8(b)所示。采用ABAQUS软件的收敛解作为参考解,节点总数为 12343,单元分布如图8(c)所示。
表2给出了点A(如图8(a)所示)在不同的时间步长下σy解的相对偏差比较。随着时间步长从0.005 s变化到0.01 s,不同时刻的应力解相对偏差相差在1.6%以内。
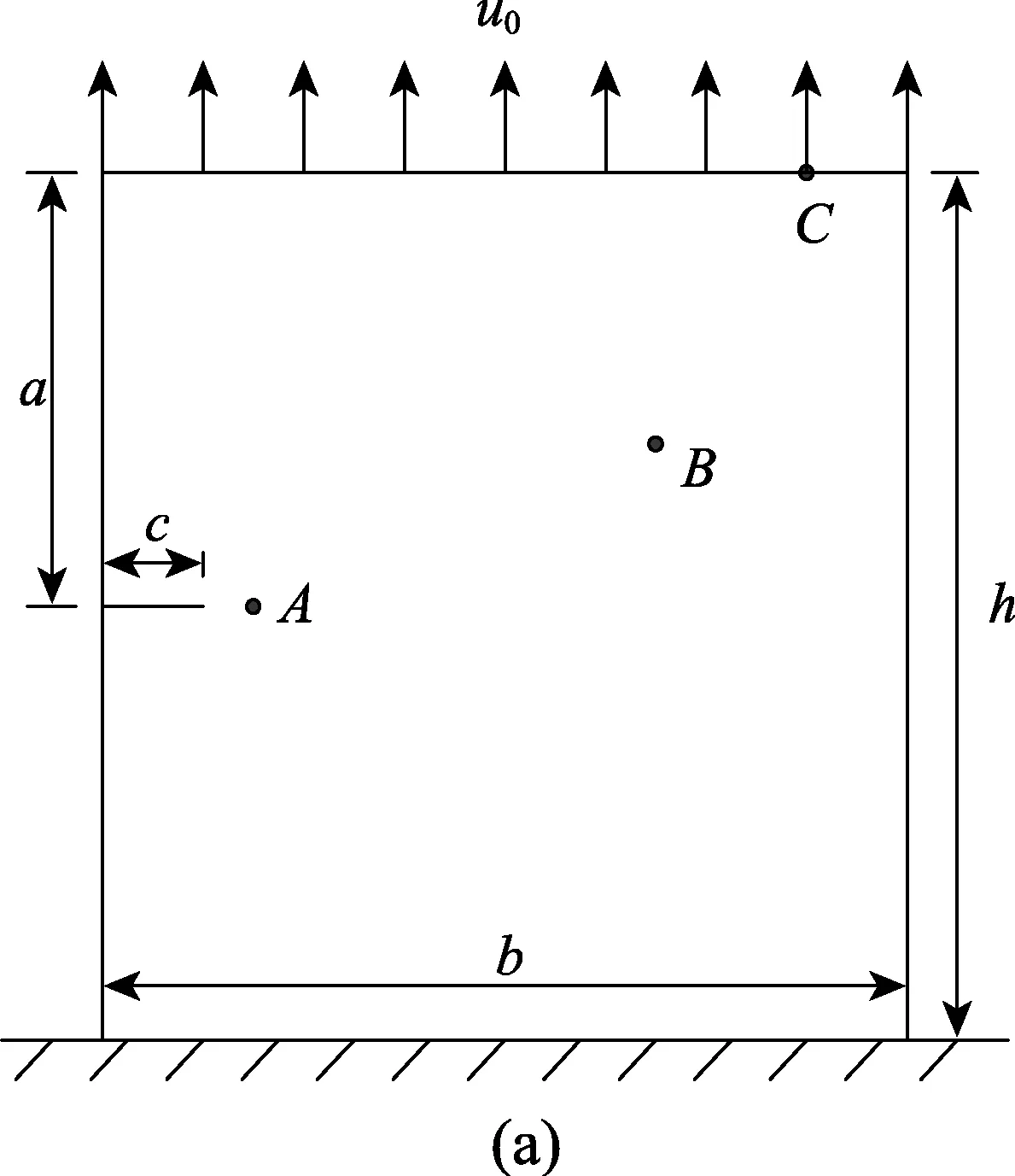
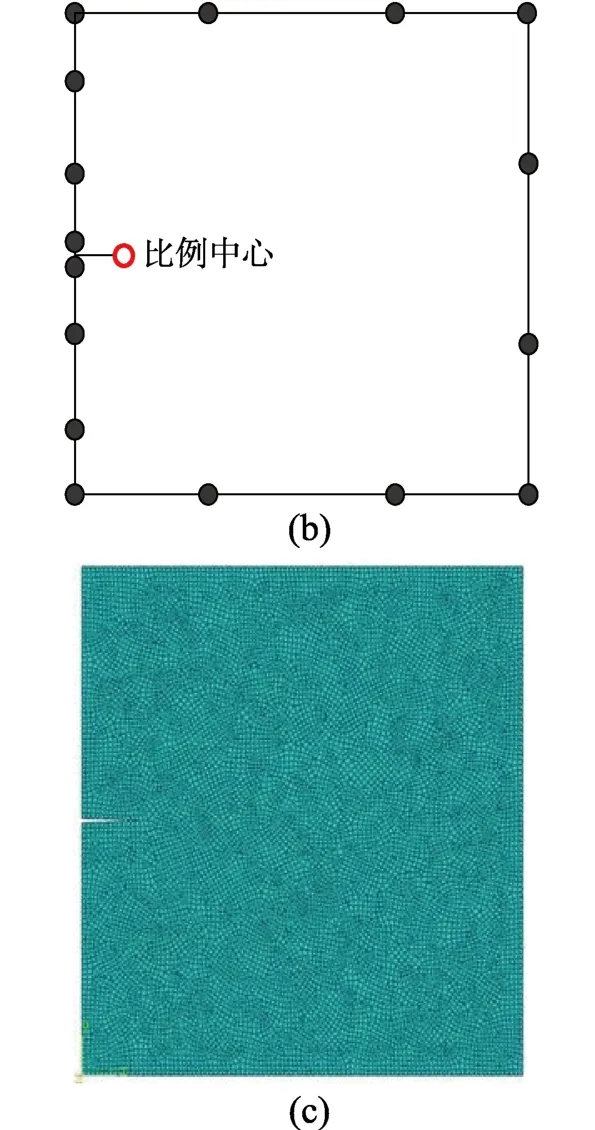
图8 带裂纹平板Fig.8 A plate with a crack
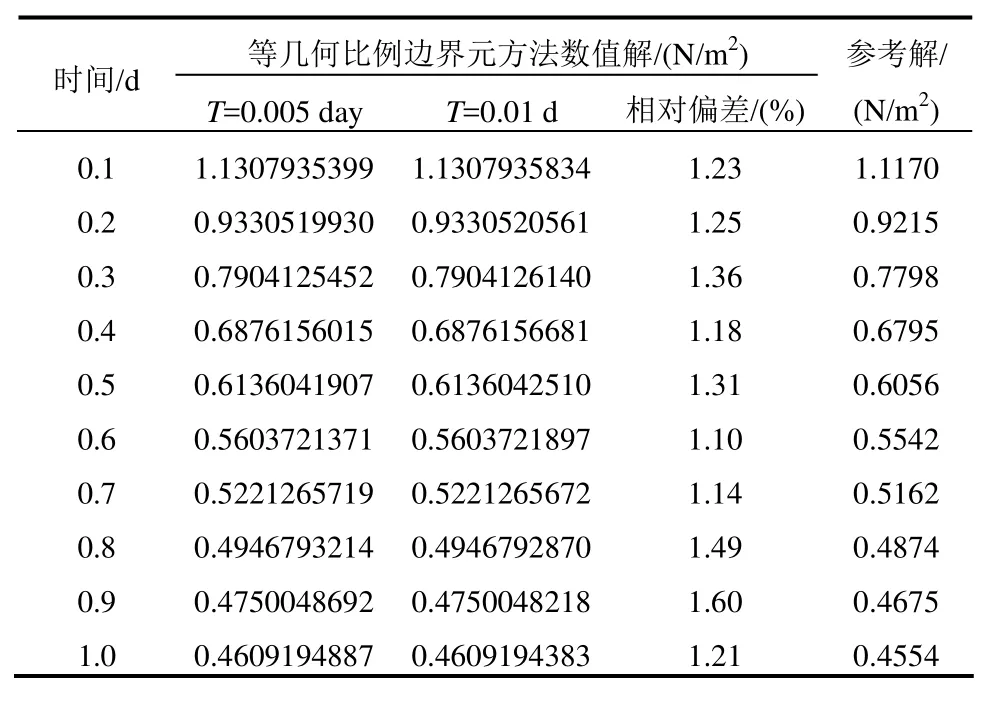
表2 不同时间步长下A点IG-SBFEM应力解的比较Table 2 Comparion for IG-SBFEM displacement solutions at point A with different time steps
图9给出了本文算法和时域非自适应算法的比较,其中非自适应计算由ABAQUS软件提供。计算结果表明,当时间步长由0.01增加到0.1时,非自适应算法的计算结果明显偏离于参考解,而本文所提的自适应算法的计算结果受时间步长变化的影响很小。
图10给出了点A、B和C的应力松弛曲线,计算结果显示,IG-SBFEM的数值解与参考解符合良好。
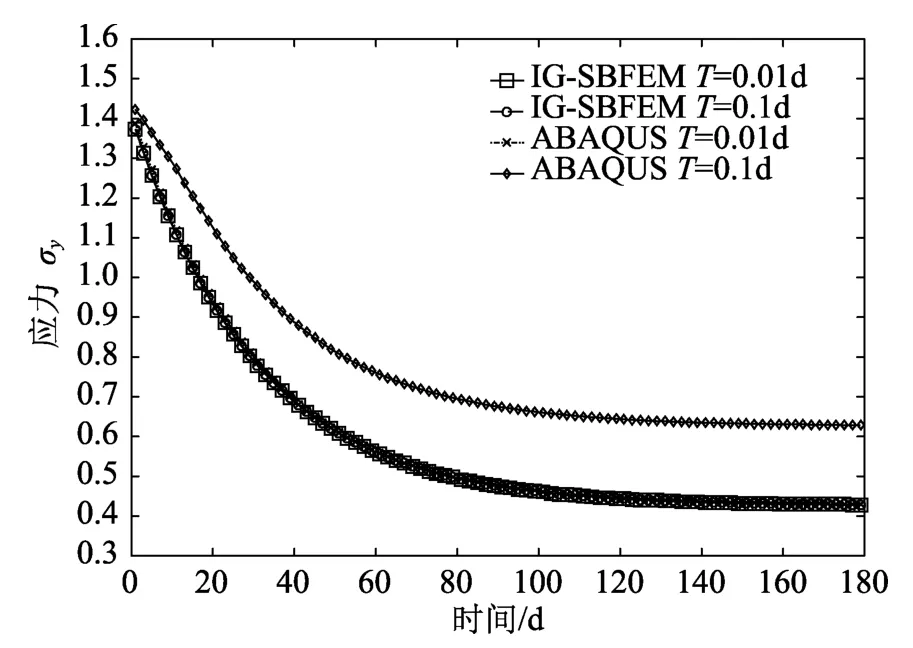
图9 本文算法和时域非自适应算法的比较Fig.9 The comparison of the proposed model with non adaptive algorithm in time domain
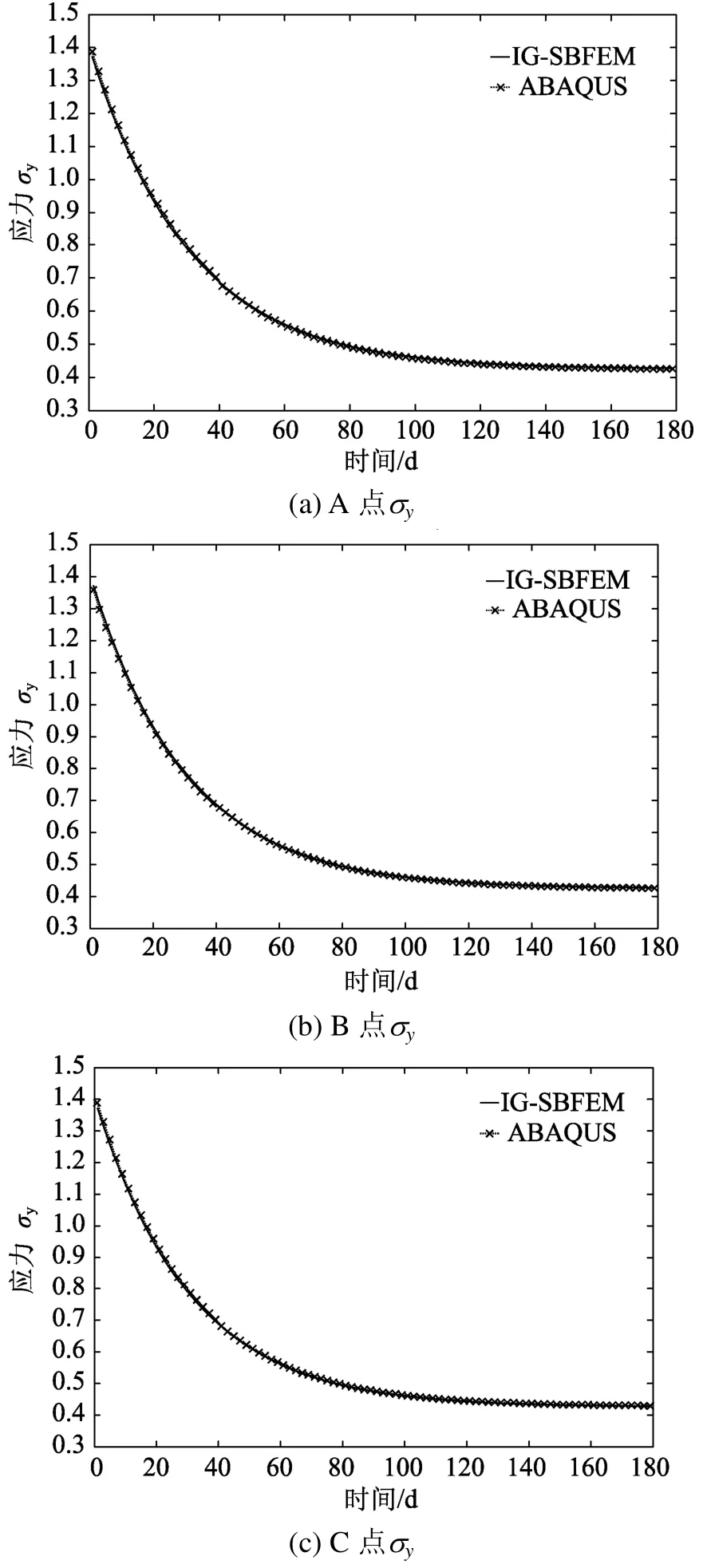
图10 应力随时间变化曲线Fig.10 The variation of stress with time
4.3 粘弹性岩体中的衬砌结构蠕变分析
考虑如图11所示的在无限域粘弹性岩体中的混凝土衬砌,衬砌内部受到作用于内壁的径向均布荷载P=1 N/m2,几何参数a=1.2 m,b=1.0 m,混凝土衬砌和岩体材料的三参数固体粘弹性参数[17]:
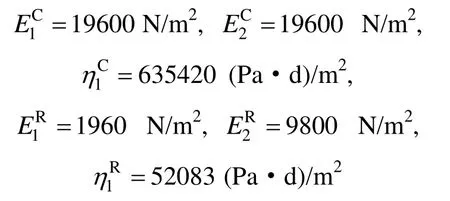
式中:上标C表示混凝土衬砌;R表示岩体。
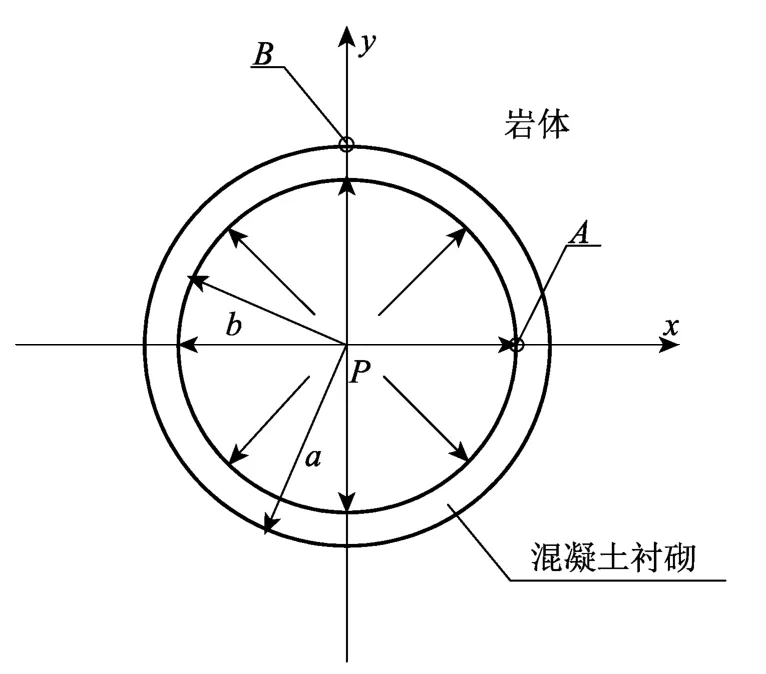
图11 无限域粘弹性岩体中的混凝土衬砌Fig.11 Circular concrete lining in unbounded viscoelastic rock
根据对称性,选取如图12所示的1/4结构进行分析,IG-SBFEM数值计算模型如图12所示,其中控制点数量为 20个,在此基础上进行节点插入加密可得到48和97个控制点的二次NURBS离散形式[34]。参考解由ABAQUS的收敛解提供,计算模型如图13所示,共使用49670个节点。
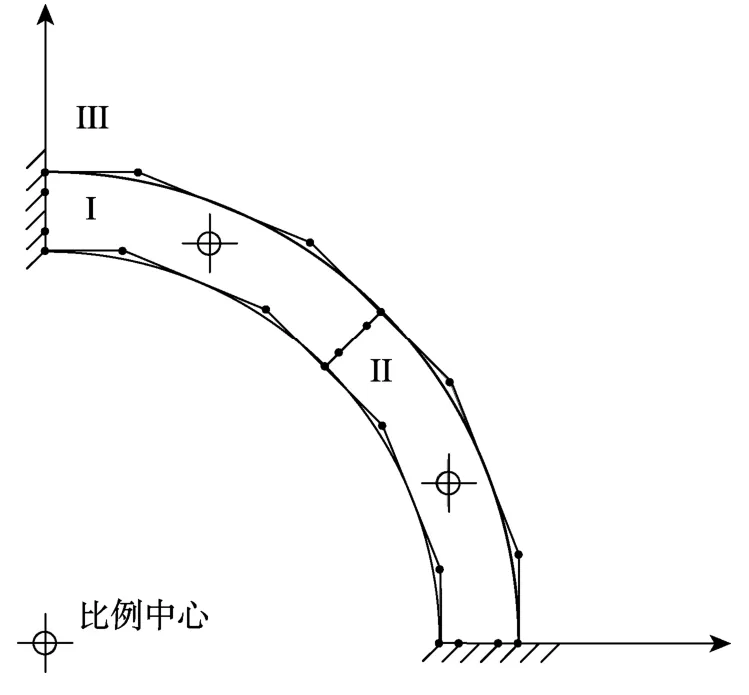
图12 IG-SBFEM数值计算模型(20个控制点)Fig.12 IG-SBFEM numerical model(20 control points)
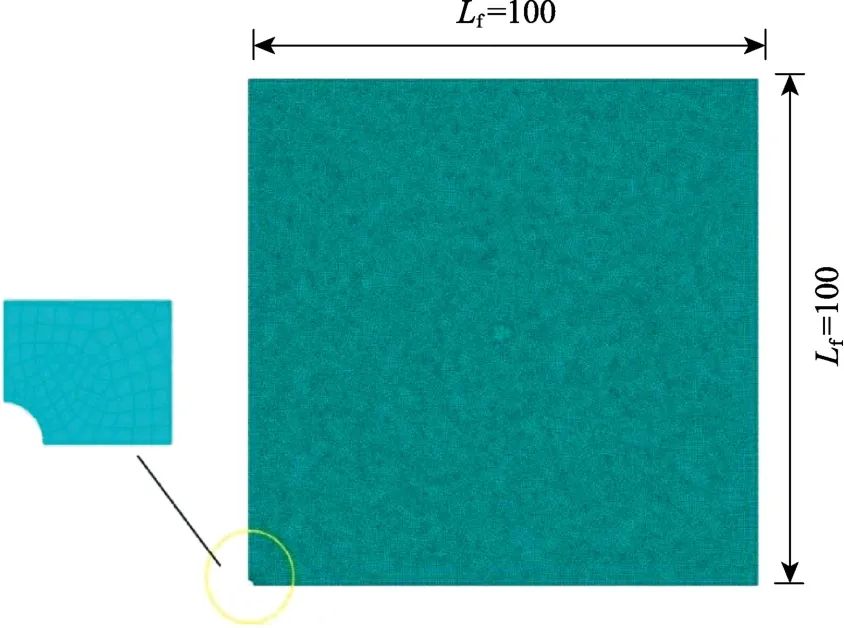
图13 有限元网格Fig.13 FEM mesh
表3给出了不同控制点数目对点A在x方向位移的影响,随着控制点数目的增加,数值解的相对偏差逐渐减小。
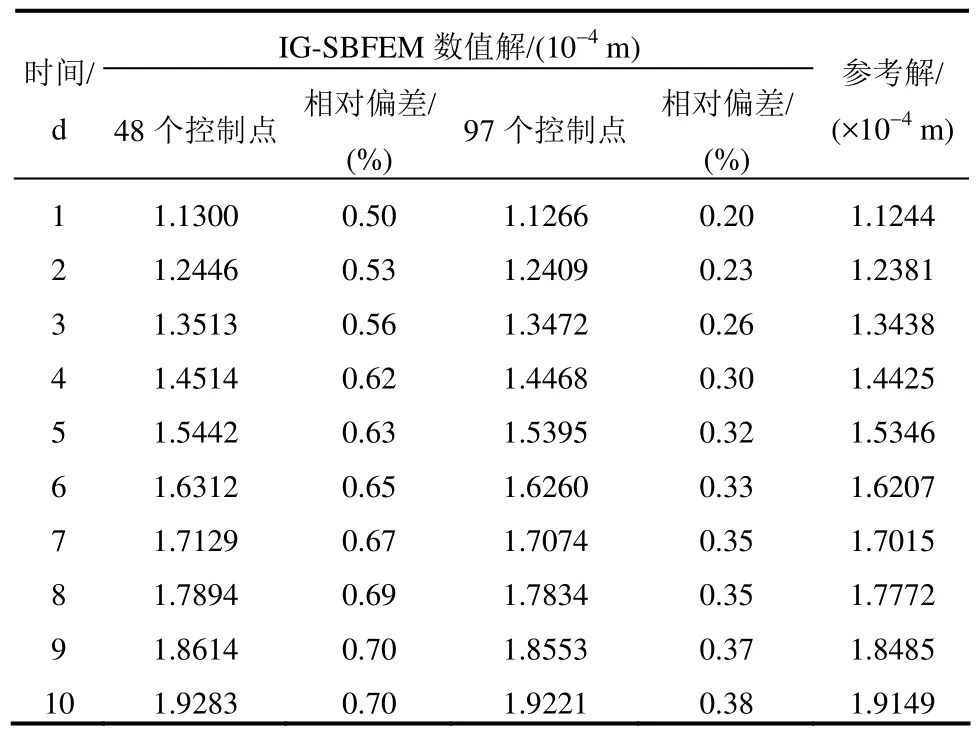
表3 不同控制点条件下的A点x轴方向位移解Table 3 Displacement solution in x-direction at point A with the different control points
图14给出了A点和B两点蠕变曲线IG-SBFEM解与参考解的比较,计算结果显示,所提方法与参考解符合良好。
4.4 计算结果小结
1)图4、图10、图14以及表1、表2的计算结果及比较表明,所提算法可对粘弹性问题进行准确有效的数值求解;
2)图6(a)和图6(b)和表1的计算结果及结果表明,当未知量数目相同时,与常规线性和二次SBFEM 相比,IG-SBFEM 具有更高的计算精度;3)由图7和表2的计算结果可见,所提算法可对不同的时间步长,通过自适应计算,保持稳定的计算精度,并通过展开阶数的调整满足不同大小误差限要求。
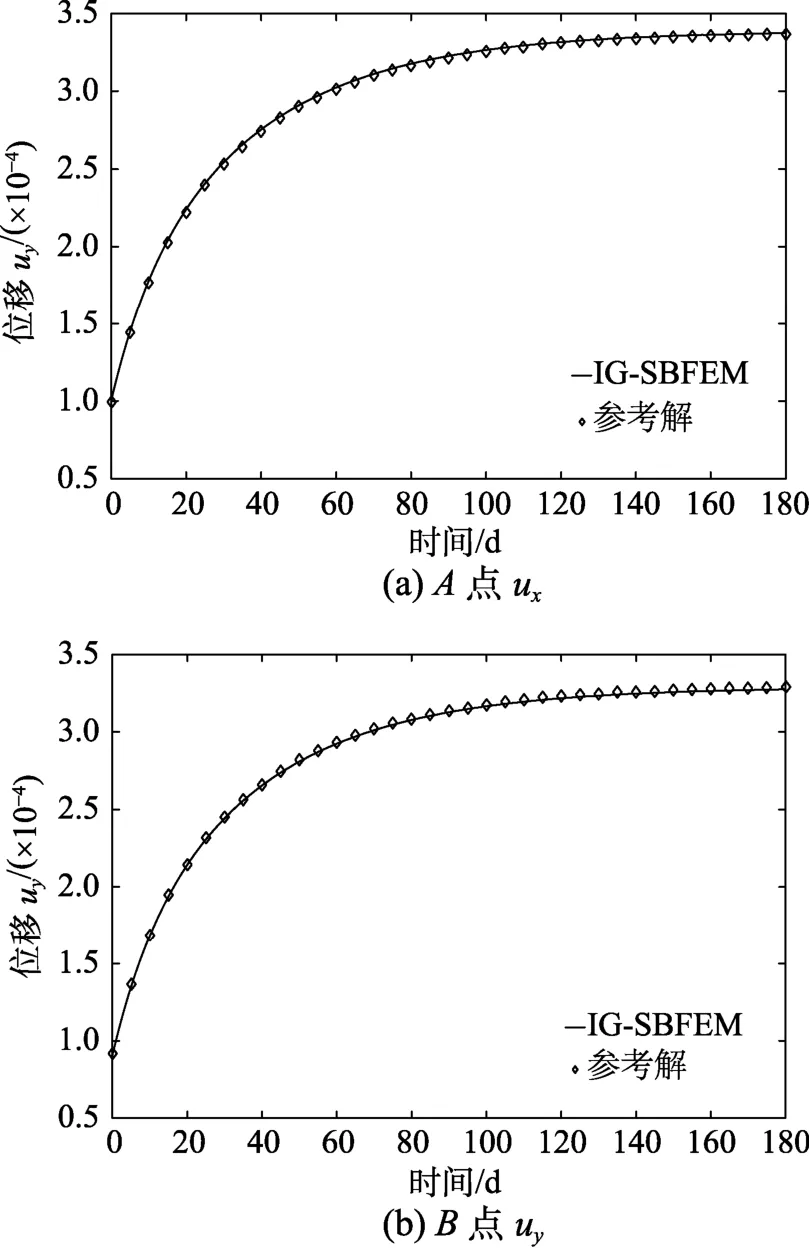
图14 A点和B点的蠕变曲线Fig.14 The creep curves for points A and B
5 结论
本文的主要贡献是集成等几何分析技术、比例边界有限元、时域分段自适应算法的优点,提出了一种新的求解粘弹性问题的时域自适应IG-SBFEM方法。所提方法将时空耦合的粘弹性性问题解耦为一系列递推形式的空间弹性问题,并建立了基于IG-SBFEM的递推求解方程。IG-SBFEM具有半解析性,可更准确地描述问题的几何模型,可将SBFEM与CAD模型无缝融合,并适于求解无限域和应力奇异性相关的粘弹性问题。所提算法时域计算精度高,对不同的时间步长可保持稳定的计算精度。数值算例的结果表明,所提方法具有良好的计算精度和收敛性。
