基于精确几何模型梁单元的螺旋弹簧刚度分析
2020-02-10齐朝晖卓英鹏国树东
张 健,齐朝晖,卓英鹏,国树东
(大连理工大学工业装备结构分析国家重点实验室,大连 116024)
螺旋弹簧在机械系统中有着重要影响,尤其在车用发动机配气机构和悬架系统等复杂机构上起着重要作用[1-2]。螺旋弹簧的刚度特性是设计弹簧的重要评价因素。
在复杂机械系统建模中,将螺旋弹簧视为单自由度振动模型或是采用将弹簧按照圈数分割为集中质量,质量与质量之间通过连接具有当量刚度的无质量弹簧[3],该方法忽略了弹簧的非线性特性,不能准确地反映弹簧的非线性刚度。采用有限元分析能获得比较精确的弹簧刚度特性,因而,有限元分析广泛应用于对弹簧特性的评价。早期建立弹簧有限元模型是利用传统梁单元建模,将弹簧分割成很多部分,每部分之间通过直梁单元连接,该方法忽略了弹簧本身是空间弯曲结构,故而弹簧模型离散的疏密程度和梁单元在弹簧中的比例都会影响计算的精度和计算速度[4]。文献[5]应用直梁单元的建模思想建立曲梁单元,证明对于螺旋弹簧结构中使用曲梁单元的精度要明显高于直梁单元,并且同等精度的情况下使用更少的单元数量。文献[6]提出了节点自由度为 6的 2节点三维曲梁有限单元模型,在一定程度上是一种高效弹簧建模方法。同时,文献[7]作为弹簧设计指导手册,对弹簧设计做出了比较系统的分析,提出了经典理论刚度公式,在其有限元分析案例中采用三维实体单元,这种分析手段方便成熟,适合于对弹簧特性的评价,但并未考虑弹簧弯曲变形对弹簧刚度的影响。文献[8]中的弹簧模型考虑了弯曲变形,但所建立的曲梁单元只适合于小变形情况。
螺旋弹簧模型应选择一种几何非线性分析方法。对于细长结构,近几年发展起来的几何非线性分析方法有绝对节点坐标法和“精确几何模型梁单元”。
绝对节点坐标法是放弃了传统梁理论中的刚性截面假设,将梁看成一种特殊实体,可精确描述单元刚体位移的变形场,它是由 Shabana[9]首次提出,由于该方法避免了对截面有限转动插值引起的各种困难,是柔体动力学研究的一个重要进展,受到了国内外学者的广泛关注[10-11]。
“精确几何模型梁单元”则是一种摒弃了小位移小转动假设的几何非线性分析方法。选取描述单元端部形心位置的位移变量和描述单元端部横截面有限转动的角度变量作为独立的描述变量,在单元域内进行插值离散。而传统“精确几何模型梁单元”只有刚性截面假设,分析细长结构的时候会出现“剪切闭锁”,结合 Bernoulli梁理论和细长梁的几何关系,可避免对截面转动矢量进行独立插值,从而避免传统方法当中的很多问题[12-15]。
本文基于“精确几何模型梁单元”提出了一种新的螺旋弹簧刚度分析方法。结合螺旋弹簧的设计构型特点和变形规律,寻找螺旋弹簧的描述参数;基于传统“精确几何模型梁单元”几何非线性分析的方法,同时增加形心线与刚截面垂直假设条件,建立弹簧系统虚功率方程,并通过数值算例进行刚度特性分析,对比与经典理论刚度计算结果、传统有限元计算结果的差异。
1 螺旋弹簧系统描述
对于任意形状的圆柱螺旋弹簧,其基本参数包含螺旋线圆柱半径ρ、高度z和极角θ,以描述弹簧截面形心位置。首先,以右手螺旋弹簧为例,在弹簧底圈中心处,建立总体基为如图1所示。
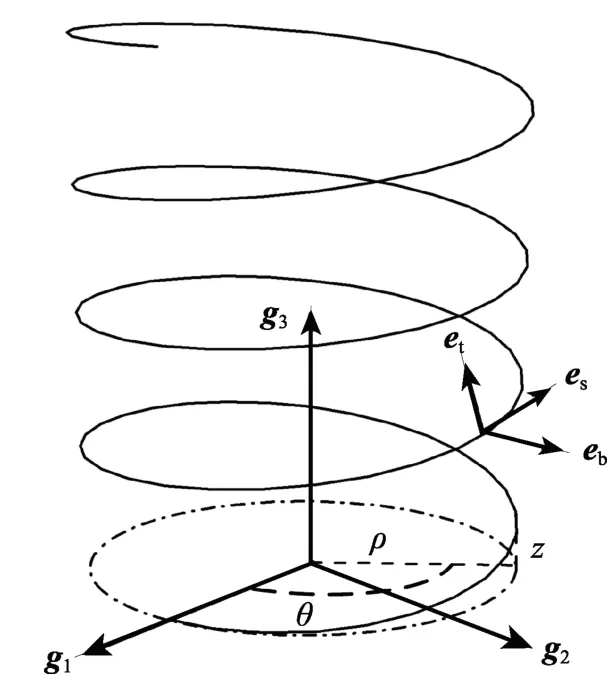
图1 总体基和截面坐标系Fig.1 Global coordinate system and section coordinate system
螺旋弹簧螺旋线的形心矢径为:
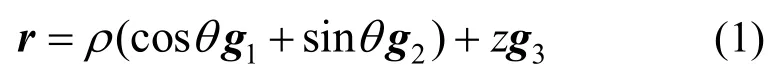
考虑圆柱螺旋弹簧只受到轴向载荷作用时,弹簧产生轴向变形,在变形过程中形心线的位置仍保持螺旋形状[7],只是基本参数螺旋线圆柱半径ρ、高度z和极角θ会发生变化,故高度z、半径ρ和极角θ是弹簧变形的状态变量。
对于已有弹簧,往往已知弹簧自由状态下高度和半径随极角变化的构型曲线。只需要通过选择适当的插值方法将构型曲线离散,便可得到螺旋线上任意一点的形心矢量。
以弹簧的每一圈为一小单元,采用Hermite插值方法,螺旋线圆柱半径插值函数为:
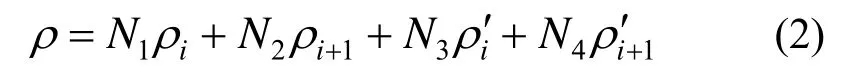
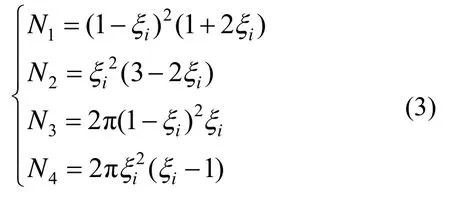
同时,保证2个样条单元之间节点处的二阶导数连续性。依据这个连续性条件,单元节点处的半径对初始极角的一阶导数表示为:
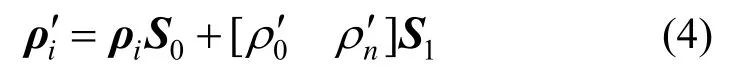
式中:ρi=[ρ0ρ1...ρn];S0和S1均为常数矩阵。
从而可将式(2)改写为:

式中:
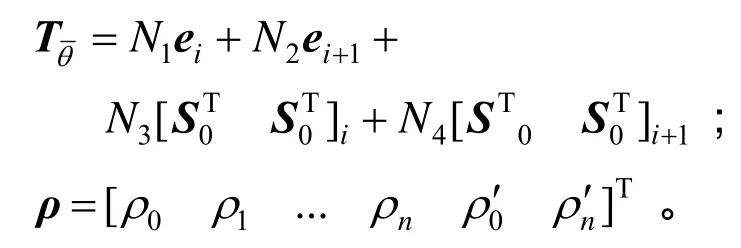
同理,弹簧螺旋线高度为:

弹簧螺旋线极角为:

假设簧丝截面为刚性截面,弹簧在压缩或者拉伸过程中,不仅弹簧螺旋线的形心矢径发生改变,而且簧丝截面也会发生相应的扭转。除形心矢径的描述变量外,还需增加一个簧丝截面的扭转角。
插值方法同上,有:

故,螺旋弹簧的完备描述参数为:
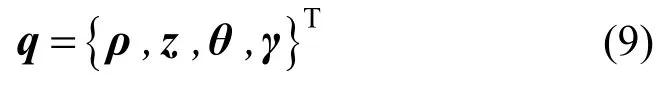
2 簧丝截面坐标系的建立
基于刚性截面假设,簧丝截面所做的运动为刚体运动,因而可以用固结于横截面的截面坐标系描述刚体截面的方位,如图1所示。截面坐标系的原点在弹簧形心线上,es轴是形心线的切线方向,另外et、eb两根轴分别为弹簧截面的形心主轴。
螺旋线形心线切矢量为:
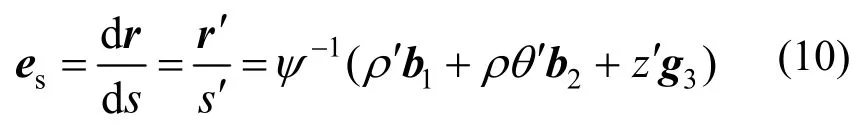
卡尔丹描述的截面法向矢量为:
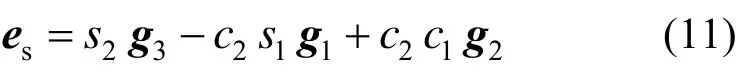
考虑弹簧细长结构特点,采用 Bernoulli梁理论,变形过程中梁截面始终保持与形心线切向垂直,截面法向矢量与螺旋线的形心线切线方向一致。通过式(10)和式(11),求得卡尔丹角为:
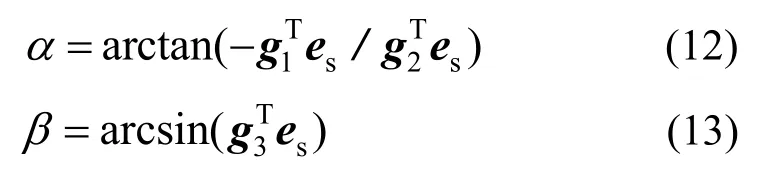
由式(12)和式(13)可知,α、β角完全由弹簧形心线的形状所决定。因而只需要用第3次定轴转动的卡尔丹角就可以描述簧丝截面的扭转。
簧丝截面的其他2个矢量为截面形心主轴,分别为:
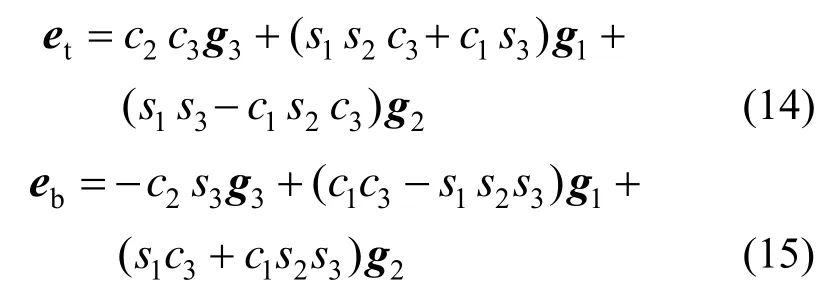
3 弹簧单元的惯性力虚功率
刚性簧丝截面的惯性力虚功率包含平动惯性力虚功率和转动惯性力虚功率两部分,在弹簧单元域(0,2nπ)内积分可得到弹簧单元惯性力虚功率。
弹簧单元平动惯性力虚功率为:
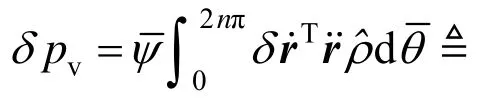
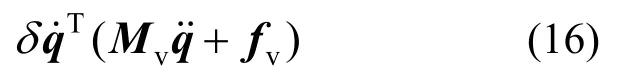
角速度具有明确的物理意义[16],有:
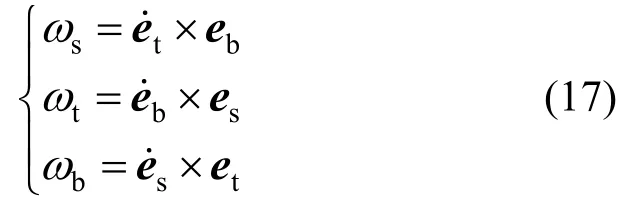
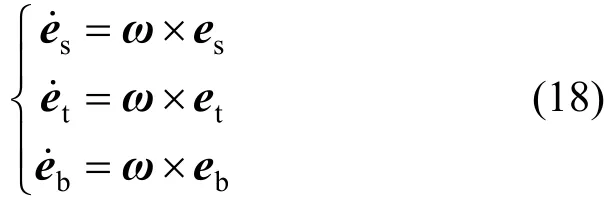
式中,截面角速度ω在连体基中的分解为:
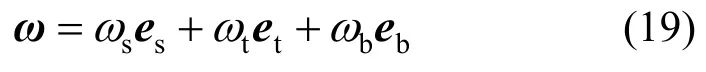
考虑到方便对比推导曲率矢量,故将截面角速度在截面坐标系下表达。
采用卡尔丹描述,在总体基下的3个转轴为:
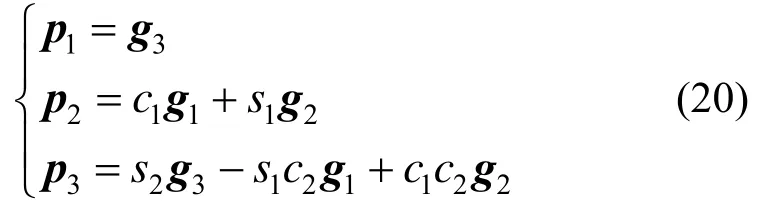
通过式(11)、式(14)和式(15)将其转化到截面坐标系下,则3个转轴为:
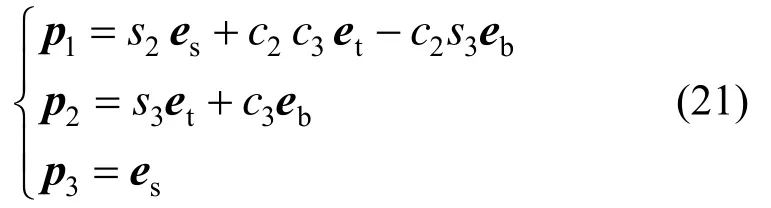
根据相继定轴转动,弹簧截面的角速度为:
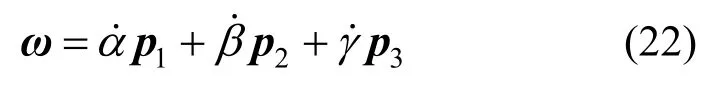
角速度矢量在截面坐标系中的分量为:
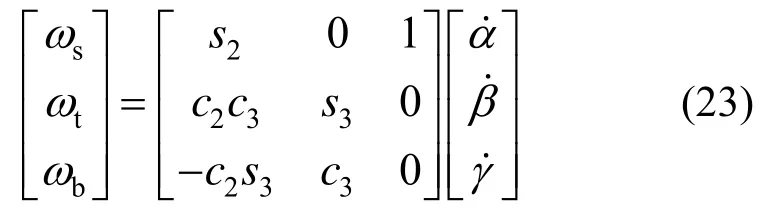
弹簧单元转动惯性力虚功率为:
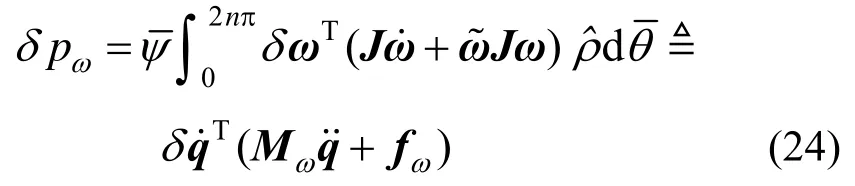
式中,J为刚截面的惯性矩张量。
4 螺旋弹簧的曲率矢量与轴向应变
螺旋弹簧是空间曲梁结构,可以用曲率矢量表征形心线的弯曲扭转程度,与角速度相同,曲率也具有明确的物理意义,曲率为:
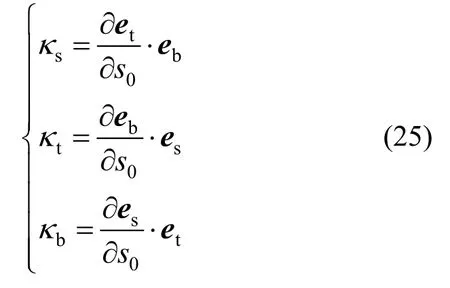
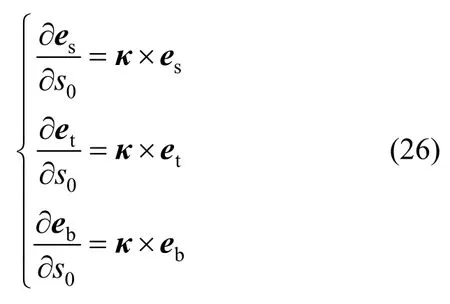
式中:s0为螺旋弹簧形心线初始弧长坐标;曲率矢量κ在连体基中的分解为:
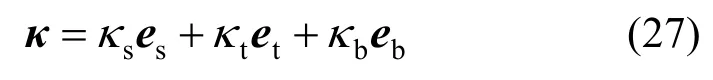
类比角速度的叠加原理,弹簧单元截面的曲率矢量为:
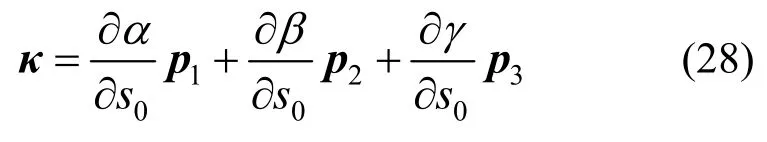
曲率矢量改写为:
曲率矢量在截面坐标系中的分量为:
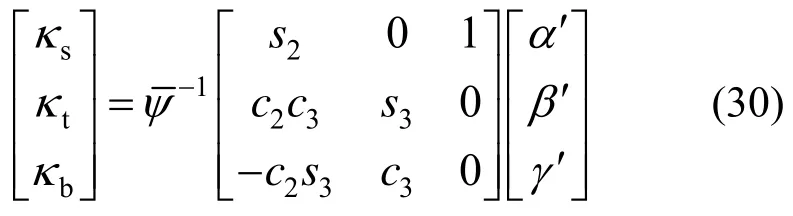
曲率矢量之所以须在截面坐标系下表达,这是由曲梁的本构关系所决定。
刚截面作刚体运动,可将曲梁微元体简化成一条形心线,梁的应变只是变形前弧长坐标s0和时间的函数。变形后弧长也是这两个坐标的函数,则曲梁的轴向应变为:
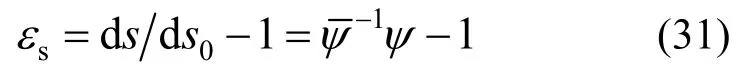
5 弹簧的变形虚功率
在弹簧中取一段长为ds0微元体,该微元体是具有初始曲率的曲梁微元体。
微元体可当成一段刚体,刚体的动力学方程为:
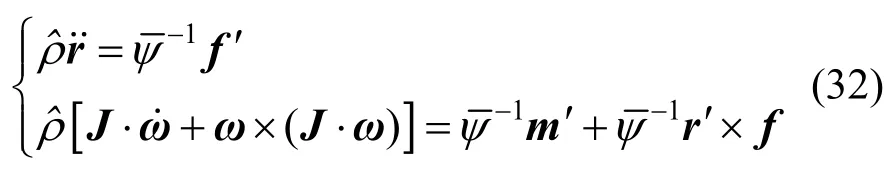
式中:m、f分别为曲梁微元体左端面合力矩和合力;
根据虚功率原理,可得微元体的外力虚功率为:
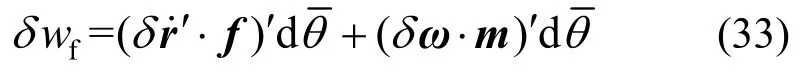
微元体的惯性力虚功率为:
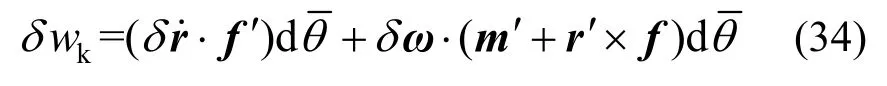
根据虚功率原理,曲梁微元体的变形虚功率为:
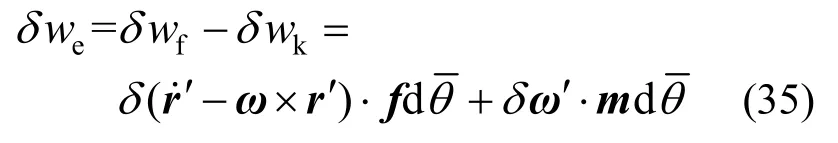
将其沿极角积分可以得到弹簧变形虚功率:
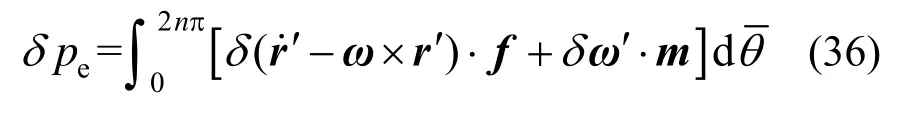
根据截面法向与截面形心线方向相同的假设条件,由式(10)和式(31)可得:

式(37)两端对时间求一阶导数,得:
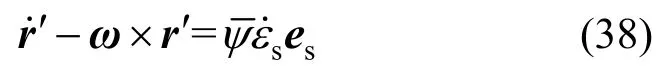
角速度ω对求一阶导数:
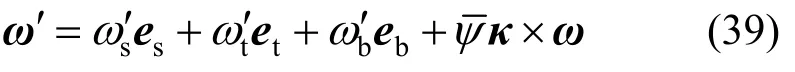
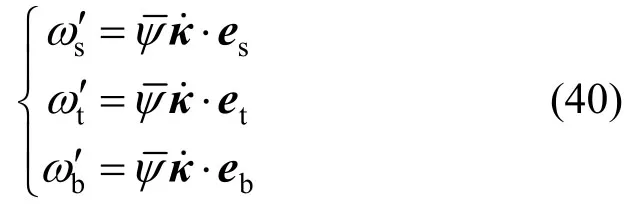
将式(40)代入式(39),有:
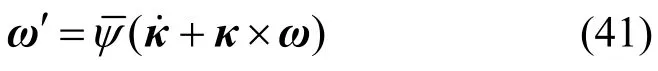
曲率矢量κ的一阶时间导数为:
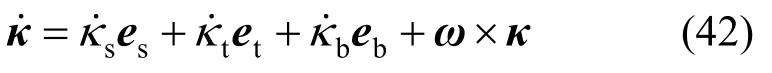
将式(42)代入式(41),则有:
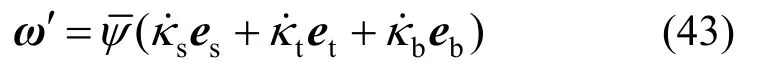
将式(38)和式(43)代入式(36),可得弹簧的变形虚功率为:
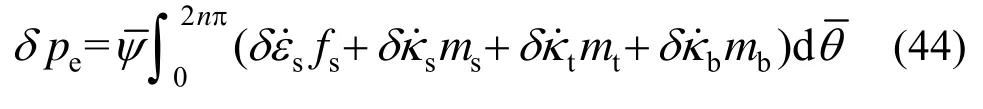
构造曲梁单元的本构关系可以描述为:

整理后,弹簧的变形虚功率为:
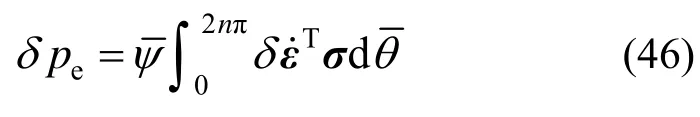
6 弹簧刚度的计算
6.1 模型降噪方法
系统动力学方程具有很强的刚性,而高频弹性振动主要源于应力的快速变化,模型降噪的方法是将应力在一个时间区间(t,t+h)内平均[17],用平均应力替换应力σ,以此来计算柔体的变形虚功率。
平均应力近似表达为:
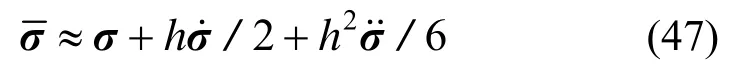
则变形虚功率为:
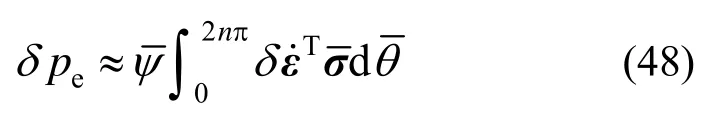
将式(47)代入式(48),变形虚功率为:
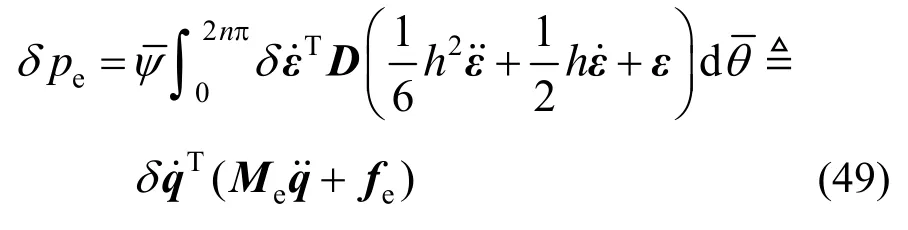
与修改前的变形虚功率相比,增加了惯性项和阻尼项,从而降低了系统的固有频率,可以获得更高的计算效率。
6.2 系统虚功率方程
弹簧刚度是通过在弹簧轴向方向上施加测试外载荷获得,在弹簧系统中外力虚功率包含重力虚功率和测试载荷虚功率。
重力虚功率为:
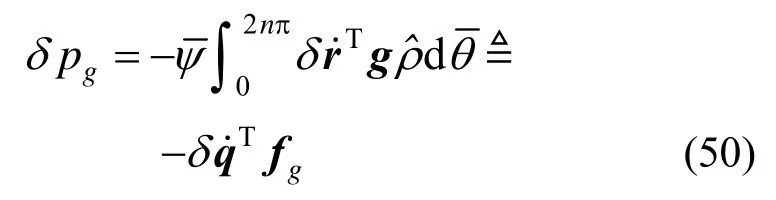
测试载荷虚功率为:
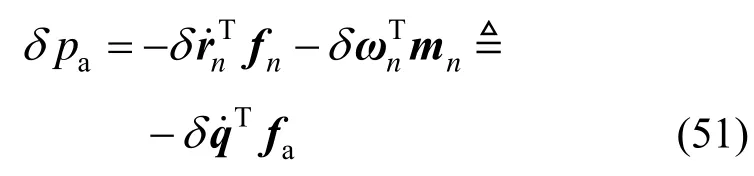
式中:fn为测试载荷;
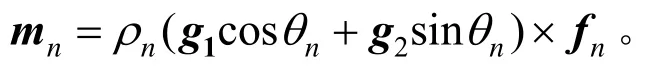
系统虚功率方程为:
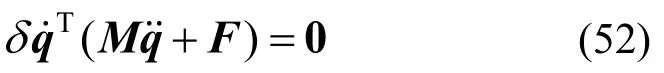
7 数值算例
算例1.圆柱压缩螺旋弹簧基本参数:中径30.4 mm,有效圈数 4,簧丝直径 4.1 mm,节距为11.94 mm,材料弹性模量2.1×105MPa,泊松比0.3,密度7800 kg/m3。
弹簧模型如图2所示,弹簧的两端圆并紧并磨平,支撑圈数为1.5。
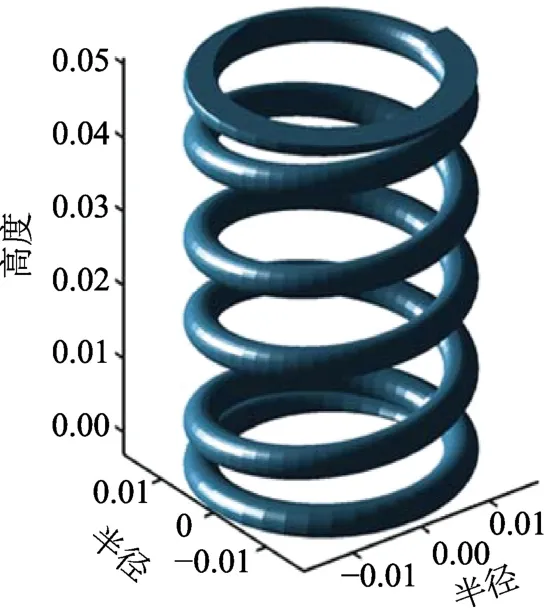
图2 弹簧模型/mmFig.2 The model of spring
弹簧模型的曲率如图3所示。由图3可知,弹簧曲率不仅在小单元内部连续,而且在每圈样条单元的节点拼接处也连续,该种弹簧单元具有很好的光顺性。
当弹簧支撑磨平面承受承载力的时候,忽略与支撑圈与活动圈的压紧,将作用载荷等效到有效圈的端部节点。
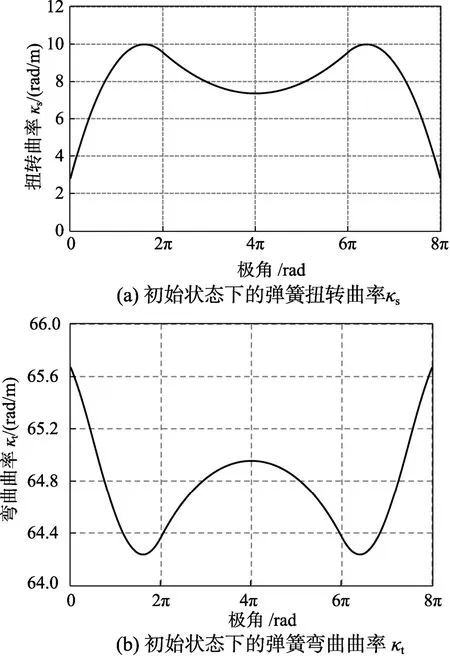
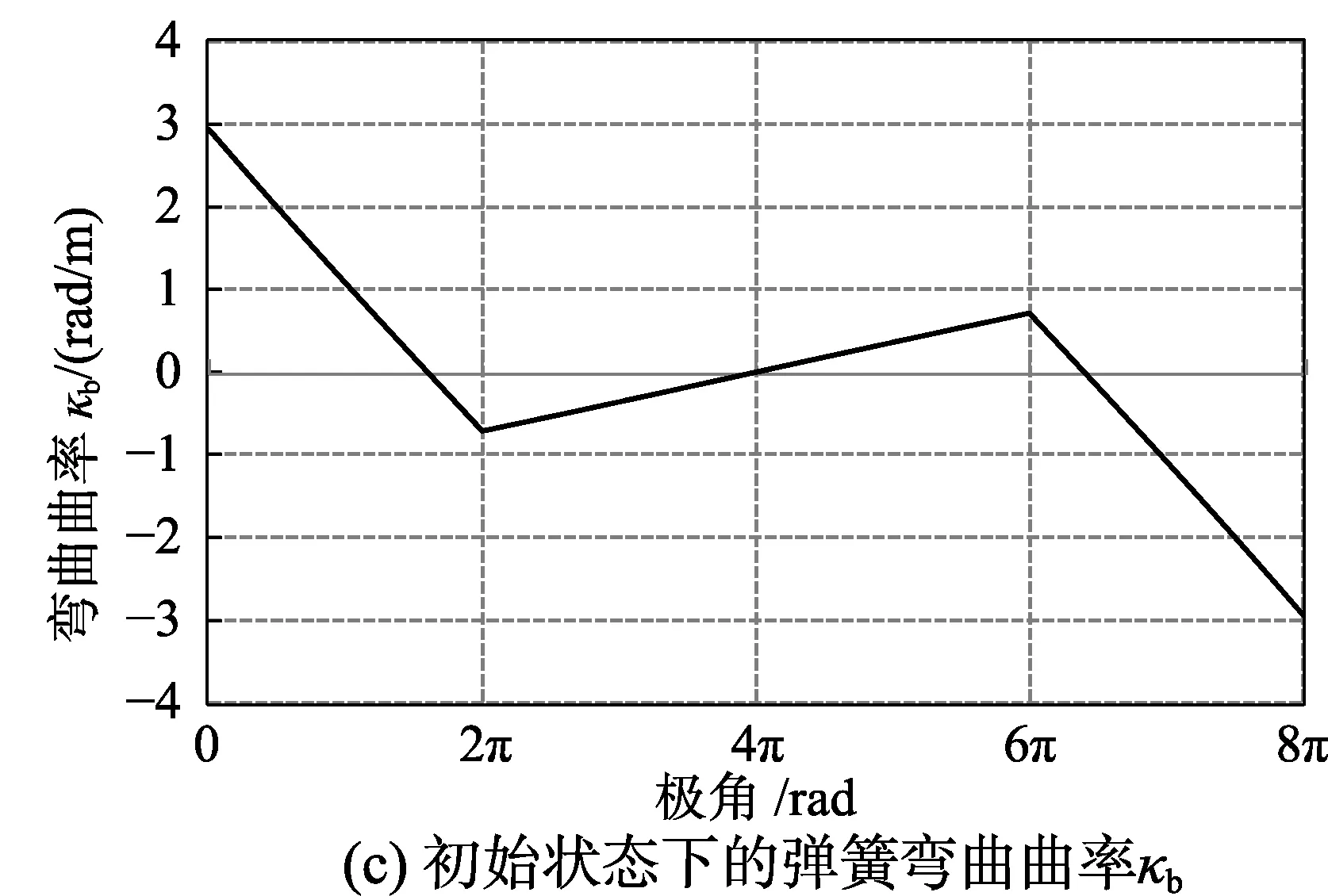
图3 弹簧初始曲率Fig.3 Spring curvature in initial state
弹簧单元底部施加固定约束,顶部平面缓慢施加过程压力载荷,最大载荷为300 N,载荷方程为:
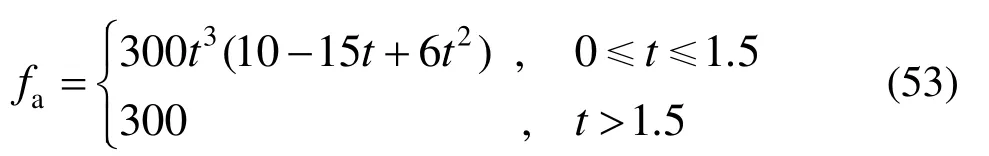
弹簧各圈高度的变化情况如下图4所示。
顶部施加压力载荷 270 N~540 N,在弹簧受压过程中,弹簧刚度变化情况,如图5所示。
由刚度变化曲线可知,弹簧在压缩过程中,弹簧的刚度是渐减的,程序计算刚度值与文献[7]评价一致。
算例2.圆柱拉伸螺旋弹簧基本参数:中径18.5 mm,有效圈数10,簧丝直径2.5 mm,节距为3 mm,材料弹性模量2.1×105MPa;泊松比0.3;密度7800 kg/m3。弹簧模型如图6所示。
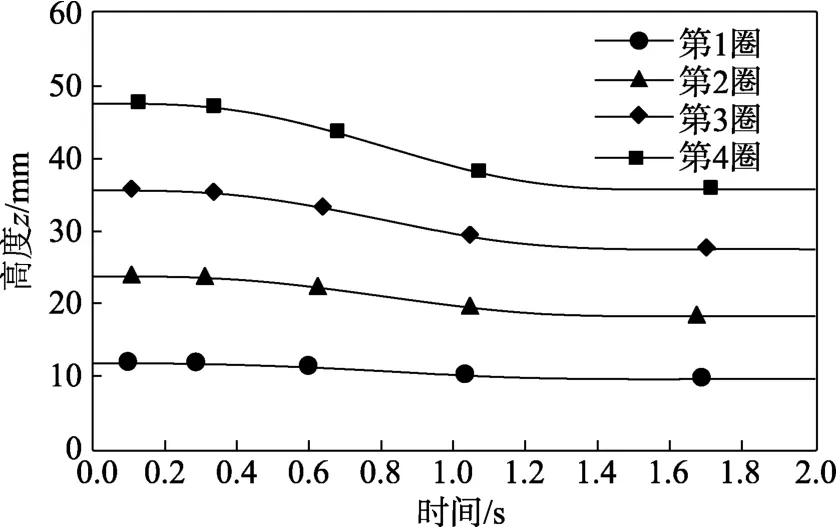
图4 压缩过程中各圈高度Fig.4 Each spring height in compression process
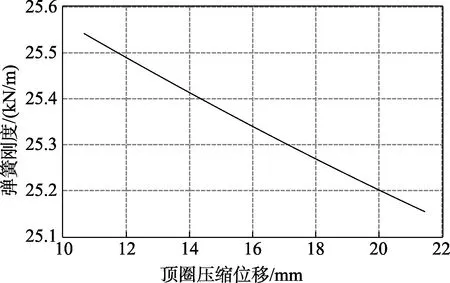
图5 圆柱压缩螺旋弹簧刚度变化曲线Fig.5 Cylindrical compression coil spring stiffness curve
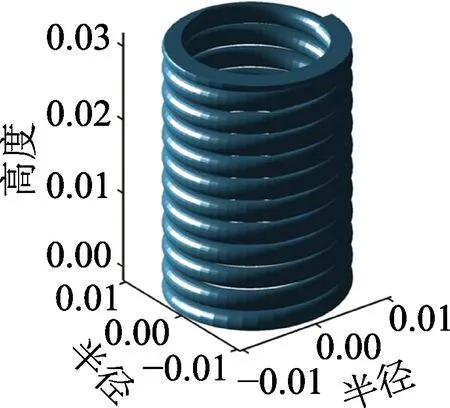
图6 弹簧模型/mmFig.6 The model of spring
底部固定约束,顶部施加拉力 100 N~500 N。刚度变化如图7所示。
由图7刚度变化曲线可知,拉伸弹簧的刚度是渐增型,程序计算刚度值与文献[7]评价一致。进一步发现,刚度并不是线性增加,而是非线性的。
算例3.圆柱螺旋弹簧基本参数:中径157 mm;有效圈数 6;簧丝直径 13 mm;材料弹性模量2.1×105MPa;泊松比0.3。顶部施加压力1000 N。将刚度仿真结果与理论值比较。
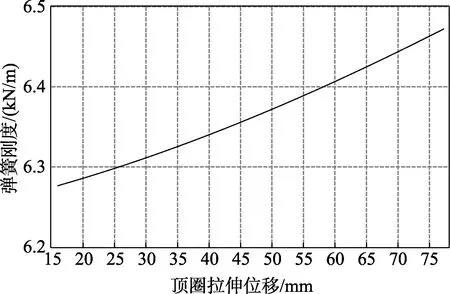
图7 圆柱拉伸螺旋弹簧刚度变化曲线Fig.7 Cylindrical tensile coil spring stiffness curve
圆柱螺旋弹簧的经典理论刚度公式为:

式中,G为弹簧材料的切变模量。
计算结果如表1所示。
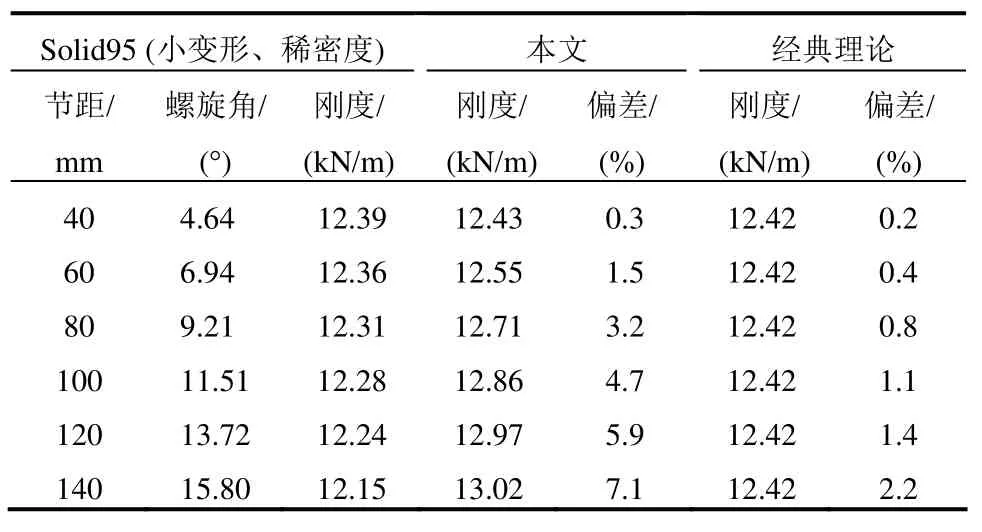
表1 弹簧刚度的仿真结果与理论值比较Table 1 Comparison of spring stiffness simulation results with theoretical values
由表1对比可知,有限元Solid95计算刚度结果与线性经典理论计算结果接近。对比节距为40 mm的 Solid95(小变形、单元数目为 156456和 7932)与 Beam189(大变形、单元数目为 50),其计算结果基本一致,可以证明该有限元方法的正确性。同时,本文方法与Solid95计算结果基本一致,可以证明本文方法的正确性。
8 结论
本文将弹簧半径、高度、极角和截面扭转角作为螺旋弹簧的描述变量,并根据设计曲线进行插值离散。基于改进后的“精确几何梁单元”建模方法,通过形心曲线切矢量和簧丝截面扭转角建立截面坐标系。应用高频弹性振动降噪方法,得到弹簧系统虚功率方程,最后求解得到弹簧刚度。通过对比传统有限元模型和经典理论刚度公式的计算结果,验证了该种螺旋弹簧刚度分析方法的合理性和正确性,并为变刚度弹簧设计做好了理论准备。
