基于改进遗传算法的自适应越区切换方案

朱 豪, 彭 艺, 张 申, 李启骞

(昆明理工大学 信息工程与自动化学院, 昆明 650504)

当高速运行的列车在相邻小区之间进行通信切换时, 要实现通信的无缝切换具有重要意义.在切换过程中, 乒乓切换、 多普勒频移等问题, 将会产生较高的信令拥堵, 使切换触发率与成功率大幅度降低, 甚至导致通信中断, 极大降低了用户的通信体验.且由于时变衰落特性对无线通信网络的影响, 将会使通信系统性能随周围环境的变化而产生较大变化.因此, 针对不同的环境, 切换过程中的判决参数将会不同, 需要自适应地调整.文献[1-2]通过建立满意通信概率(satisfactory communication probability, SCP)模型解决了列车高速移动过程中产生的多普勒效应问题, 并提出了基于速度的联合判决算法, 但该算法未考虑迟滞容限值与速度的动态变化关系；文献[3]提出了一种基于模糊逻辑的切换算法, 对切换过程中的门限值做一个动态调整, 使切换能达到更好的效果；文献[4]首先分析比较了切换过程中可能遇到的相关参数, 然后通过多属性决策理论对不同场景下的参数进行相关仿真, 进一步分析了切换时延和切换次数等因素对切换参数的影响；文献[5]根据列车的实时地理位置, 提出了基于距离信息的切换算法, 通过迭代法调整参考信号接收功率(reference signal receiving power, RSRP)的门限值; 文献[6]提出了一种基于RSRP和参考信号接收质量(reference signal receiving quality, RSRQ)的联合判决, 能在信号接收强度较低的情形下, 选择信号质量最好的基站执行切换.

虽然目前已有的切换技术都能在某种程度上提高切换的性能, 保障基本的通信质量, 但在高速铁路多变复杂的运行环境中, 信道衰落、 多普勒频移、 车厢穿透损耗等问题仍然存在[7-11].要满足高速移动场景下高质量、 高可靠的通信要求, 现有的切换算法中, 频繁的乒乓切换、 较大的误码率等问题仍较严重, 且迟滞容限值也不能根据列车速度的不断变化而自适应地调整.

针对上述问题, 本文将遗传算法应用到越区切换技术中, 以遗传算法为基础, 在高速特性下, 对切换判决过程中的相关参数进行优化, 针对不同运行速度动态选择出能满足快速切换需求的迟滞容限值, 并引入SCP, 当列车在小区之间移动时, SCP值达不到要求的将不能接入下一个小区, 以保障良好的通信质量.

1 系统模型

1.1 基于RSRP的迟滞容限

图1 切换示意图

考虑如图1所示的切换示意图, 当列车以速度V行驶至A点时, 触发切换.假设列车行驶速度为Vkm/h, 在AB重叠区内完成一次切换所需的时间为ts, 则切换带Llap的长度可表示为

(1)

列车在由基站eNodeBi小区覆盖范围向基站eNodeBj移动的过程中, 以源基站与铁路的垂直交叉点为原点, 则列车驶离源基站xkm时, 所接收到的来自源基站eNodeBi和目的基站eNodeBj的RSRP值分别为

R(i,x)=PteNodeBi-PL(i,x)-A(i,x,σ),

(2)

R(j,x)=PteNodeBj-PL(j,x)-A(j,x,σ),

(3)

其中:PteNodeB表示基站的传输功率, 基站的发射功率相等, 即PteNodeBj=PteNodeBi;A表示服从高斯分布的阴影衰落, 均值为0, 方差为σ;PL(i,x)和PL(j,x)分别表示源基站和目的基站传播至列车驶向x处时的路径损耗.本文使用Hata-Okumura模型计算路径损耗, 表达式为

PL(i,x)=69.55+26.16lgf-13.82lgHb+(44.9-6.55lgHb)lgx-α(hm),

(4)

其中:f为载波频率;Hb为基站天线高度;α(hm)表示移动台(本文中指列车)的天线高度因子, 在不同环境中具有不同的传播模型,

(5)

在列车行驶过程中, 列车的RSRP来源于基站之间的发射功率, 阴影衰落、 路径损耗作为接收功率的影响因子, 由于基站之间具有相同的发射功率, 故列车在两基站之间的RSRP差值可表示为

(6)

其中:x表示移动终端在铁轨上的位置;PL(i,x)和PL(j,x)分别表示源基站到移动终端的路径损耗和目的基站到移动终端的路径损耗.本文忽略局部阴影衰落A(j,x,σ)和A(i,x,σ)的影响, 故RSRP差值可表示为

PT=R(j,x)-R(i,x)≈PL(i,x)-PL(j,x).

(7)

定义一个门限值U表示RSRP的迟滞容限, 只有当RSRP差值不小于该门限值U时才能触发切换, 即

PT≥U.

(8)

在列车进行切换过程中, 用αdB/km表示源基站的功率损耗率,βdB/km表示目的基站的功率损耗率.当列车在切换带Llap间行驶时, 来自源基站和目的基站的功率损耗分别表示为

(9)

(10)

则RSRP差值可表示为

(11)

化简得

(12)

为了适应列车高速的需求, 切换触发后必须保障切换能有足够的时间执行, 故迟滞容限大小可调整为

μ=U-δ.

(13)

1.2 基于RSRQ的迟滞容限

列车在切换带中运行时, 会同时接收到来自源基站PteNodeBi和目的基站PteNodeBj的接收信号质量RSRQ, 若此时列车接收到来自基站PteNodeBi的RSRQ较高, 说明此时列车的通信质量较好, 不适合进行切换, 为了不浪费资源, 则应根据实际情况动态调整RSRQ的切换迟滞容限, 反之亦然.RSRQ的迟滞容限值调整公式为

(14)

其中: ΔH和ΔL分别表示最优和最差信道质量;rH和rL分别表示最大和最小迟滞容限；S表示速度参数,

(15)

1.3 速度-满意通信概率

为反映基站发射与接收信号之间质量的优劣, 需用满意通信概率模型进一步研究列车的切换算法. 定义列车在运行过程中由于速度变化而产生的通信失败现象为速度-不满意通信事件.由于该事件出现的方式是随机且独立分布的, 且速度与误码率有关, 故该事件在单位时间内的出现次数服从Poisson分布,

(16)

其中:k为出现次数;λ为Poisson分布的均值和方差,λ=a(Pb-Pstd),a为待定系数, 经过相关数据测试分析, 可得a的取值一般为106.

定义速度-不满意事件次数小于临界速度-不满意通信事件次数的概率为速度-满意通信概率, 可表示为

(17)

其中,NPstd表示单位时间内发生误码的次数, 由于误码是导致通信失败的最重要原因, 所以NPstd也称为不满意通信事件的次数.在GSM-R国际无线通信标准要求中, 通常Pstd的下限取为0.008.当列车以恒定速度V从源基站PteNodeBi向目的基站PteNodeBj移动时, 所有满意通信概率达不到门限值的小区将不能接入.

2 基于遗传算法的效益选择方法

2.1 改进算法

遗传算法是模拟生物在自然环境中的遗传和进化过程而形成的一种并行、 高效、 全局搜索方法.与传统算法相比, 遗传算法具有对参数的编码进行操作、 不需要推导和附加信息、 寻优规则非确定性、 自组织、 自适应和自学习等特点.当染色体结合时, 双亲遗传基因的结合使得子女保持父母的特征；当染色体结合后, 随机的变异会导致子代与父代的不同[12-13].本文采用遗传算法进行迟滞容限门限值的选择, 算法步骤如下：

1)随机生成初始种群U={U1,U2,…,UN}, 种群规模为N,U∈[0,20].

2)根据效益函数计算效益矩阵A=(fx1,fx2,…,fxN),

(18)

其中:V表示列车行驶的速度;α和β分别表示来自源基站和目的基站的功率损耗率.速度越大, 效益值越大, 不同速度V对应不同的效益值.

3)根据设定好的适应度函数计算出第NPstd代全部个体的适应度值pi, 用矩阵P=(p1,p2,…,pn)表示.用速度-满意通信概率表示适应度函数为

(19)

其中:k为出现次数;NPstd为不满意通信事件的次数;λ为Poisson分布的均值和方差.

4)根据适应度函数对种群中每个个体的适应度值进行排序, 并采用轮盘赌算法进行选择, 选择出与效益值f(xi)适应度最高的适应度值pi.在该选择算法中, 适应度高的值较易被选到, 反之, 适应度低的值将会被淘汰.

5)根据选取的效益值, 选取适应度最高的两个个体以概率Pc进行染色体的交叉变异, 生成新一轮的种群, 并更新为种群Ui={U11,U22,…,UNn}.

6)循环计算步骤1)～6), 不断更新新一代的种群群体, 并记录每一代种群中适应度值最高的个体f(xi).若达到设定的最大迭代次数, 则停止运算, 当前记录的个体即为算法的最优解.

2.2 切换方案分析

当列车在PteNodeBi覆盖小区行驶时, 存在小区内同频干扰的影响, 该干扰可表示为

(20)

当列车行驶到距离源基站PteNodeBi距离xkm时, 所接收到的信噪比为

(21)

其中:N0表示噪声密度;BW表示信道带宽.同理, 接收到来自j小区的信噪比可表示为

(22)

列车行驶过程中, 接收到的来自PteNodeBi的RSRQ值可表示为

(23)

接收到的来自PteNodeBj的RSRQ值可表示为

(24)

本文采用基于接收信号功率RSRP和接收信号质量RSRQ的联合判决算法, 用P1表示满足RSRP切换迟滞容限的概率,P2表示满足RSRQ切换迟滞容限的概率,P3表示RSRP达到满意通信概率的概率,P4表示RSRQ达到满意通信概率的概率, 则有：

从而本文算法的切换触发率可表示为

Phandover=P1P3+(1-P1)P2P4.

(29)

切换成功率是指切换过程中通信未发生中断的现象, 用η表示信噪比门限值, 则切换成功率可表示为

Psuccess=Phandover·P(SINR(x,i)≥η)·P(SINR(x,j)≥η).

(30)

图2为基于遗传算法的迟滞容限选取流程.

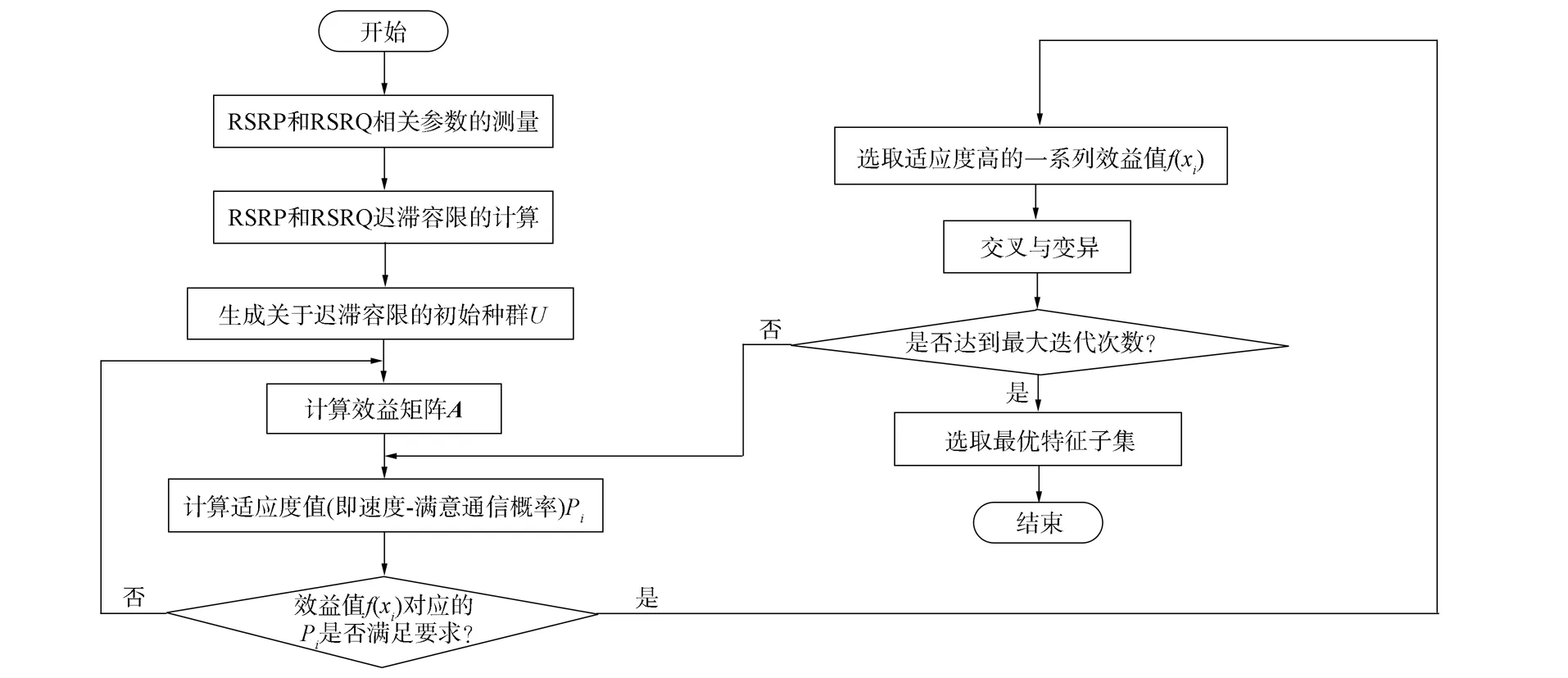
图2 基于遗传算法的迟滞容限选取

3 仿真实验

3.1 仿真参数的配置

本文采用MATLAB进行仿真验证, 由于较大的群体规模将会增大计算复杂度, 故本文遗传算法群体规模取200, 为了得到最优解, 交叉与变异概率分别取为0.8和0.1, 最大迭代次数取200次.仿真过程中采用如下参数：基站间距为4.8 km, 基站覆盖半径为3 km, 载波频率为2 GHz, 信道带宽为1 MHz, 测量周期为500 ms, 基站发射功率为43 dBm, 基站天线高度为30 m, 列车天线高度为1.5 m, 阴影衰落偏差为4 dB, 阴影相关距离为50 m, 噪声密度为-174 dBm/Hz, 切换执行时间为0.5 s, 一般切换迟滞值为3 dB, 最大RSRP迟滞值为20 dB, 最小RSRP迟滞值为3 dB, 最优信道质量为60 dB, 最差信道质量为5 dB, 信噪比门限值为-35 dB.

3.2 仿真结果分析

下面实验分析不同速度下的速度-满意通信概率.将传统RSRP的迟滞容限与本文用遗传算法迭代出的迟滞容限进行对比, 并对比传统切换方案与本文切换方案的切换触发率与切换成功率, 结果分别如图3～图7所示.

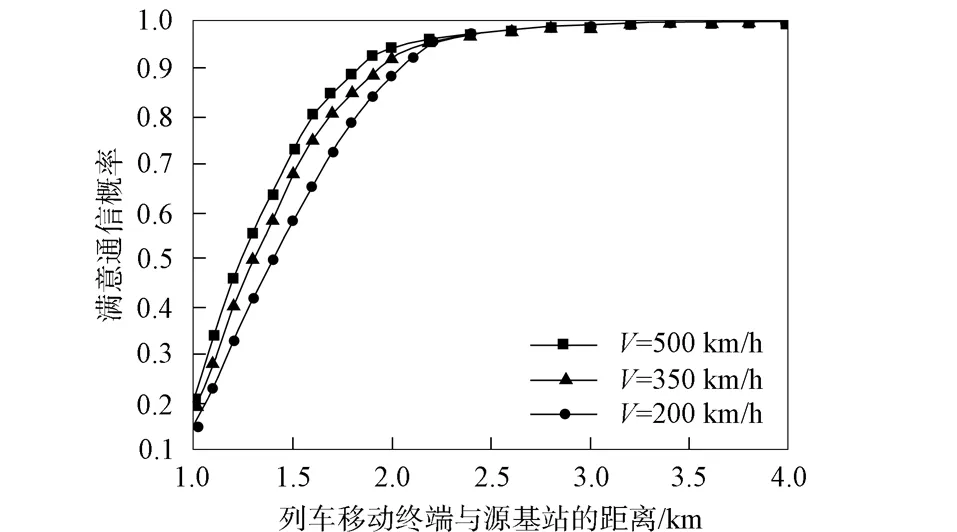
图3 不同速度下的满意通信概率

图4 不同速度下的RSRP迟滞容限

图5 不同速度时迟滞容限值与距离的关系

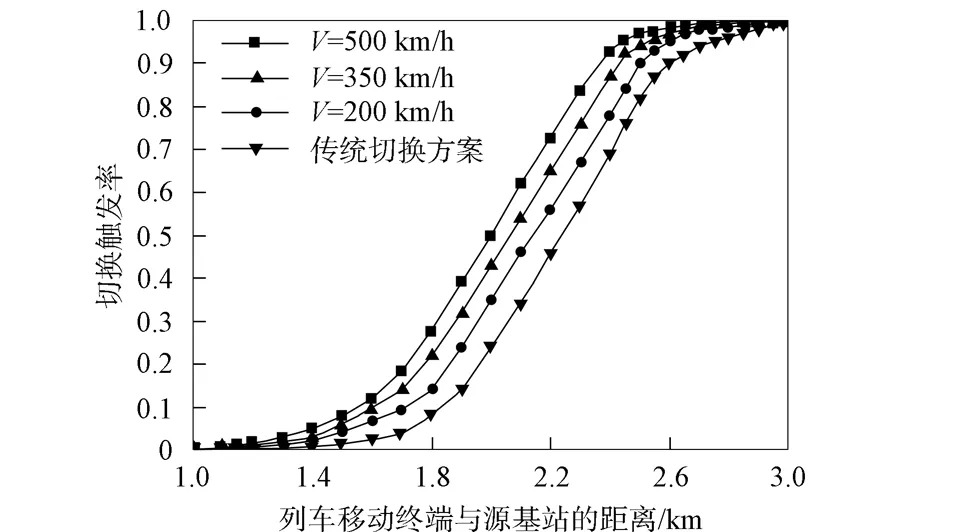
图6 不同速度下的切换触发率比较

图7 不同速度下的切换成功率比较

图3为不同速度下的速度-满意通信概率变化曲线.由图3可见, 随着列车的移动, 距离目的基站的距离逐渐缩小, 误码率逐渐减小, 当列车驶离源基站约2 km时, 速度-满意通信概率基本维持在90%以上, 达到2.5 km时, 逐渐接近于1, 很好地达到了预期效果.图4为传统RSRP的迟滞容限值与列车速度之间的变化关系.由图4可见, 迟滞容限基本与列车速度呈线性关系, 一般情况下, 大多选择3 dB作为固定的切换触发门限, 但这并不适合速度高速变化的列车运行场景.当列车速度达到400 km/h或更高时, 显然3 dB不再适用, 将会导致不必要的切换延时, 影响通信质量.图5为本文采用遗传算法迭代出的一系列迟滞容限曲线.由图5可见, 随着列车与源基站之间距离的不断变化, 迟滞容限值也不断变化, 可以更好地触发切换, 列车距离源基站越远, 容限值也变得越小, 由于设置了最小迟滞容限值, 故降低至约2.2 dB时不再变化, 从而可保证不必要切换(乒乓切换)现象的发生.

由图6和图7可见, 在列车初驶入重叠区的过程中, 由于距离目的基站的距离较远, 列车接收到的来自源基站的接收信号还远大于来自目的基站的接收信号, 所以基本不会触发切换, 导致切换的不执行, 因此初期的切换触发概率和切换成功率都较低；当列车距离目的基站越来越近, 开始触发切换, 切换触发率与成功率都快速提高, 速度越高, 切换的触发率越高.与传统切换方案相比, 本文切换算法在切换触发率和成功率方面都有较大幅度的提高.

综上所述, 本文主要研究了高速铁路场景下通信系统中的越区切换技术.通过越区切换能保证列车在高速运行环境中的不间断通信, 从而提高乘客的服务体验.本文在已有研究成果的基础上, 提出了一种基于改进遗传算法的自适应联合判决切换算法, 并对该算法进行了仿真分析, 分析了列车速度分别在200,350,500 km/h三种高速下的各种变化关系.仿真结果表明, 与传统切换方案相比, 该方案可实现提高切换触发率和切换成功率的目标, 能达到较高的满意通信概率.