地震作用下的液化砂土地基PHC管桩动态响应

陈晓军，陶桂兰，钱金炜

(河海大学 港口海岸与近海工程学院，江苏 南京 210098)

高桩码头大部分位于沿海地区和江河地区，软土和饱和土层分布广泛，地质条件不佳、承载力低，导致码头在地震作用下容易发生损伤。刘惠珊等[1]总结了日本几次大地震桩基震害，认为地震作用下土体产生液化是导致桩基结构破坏的重要原因之一。高桩码头的重心位置位于泥面以上，上部结构的质量占比高，承受较大的地震惯性力，因此高桩码头的地震破坏主要发生在下部桩基[2]。国内外相关学者用桩单元模拟实心方桩作为研究对象来进行数值模拟，李雨润等[3]对3行×3列群桩进行振动台试验及数值模拟，通过施加不同峰值加速度的地震波，监测振动台台面加速度、台面位移、桩顶承台加速度和承台位移，并与试验数据进行对比分析研究。江开渡等[4]以液化场地桩基变形为研究对象，探讨了混凝土桩桩身弯矩和桩-土相互作用力在地震作用下的变化以及液化作用对桩、土位移的影响，并对群桩中的角桩、边桩和中心桩弯矩幅值进行对比。目前PHC管桩在可液化地基上动态响应及抗震特性的研究则不是很多。PHC管桩由于其承载力高以及抗弯、抗剪和抗裂性能高的优点[5]而越来越多地被应用于高桩码头，本文采用有限差分软件FLAC3D建立实体土和实体PHC管桩的模型，对地震作用下液化地基上PHC管桩进行研究，通过动力计算与结果分析，探讨地震作用下液化砂土地基PHC管桩动态响应。

1 工程概况

该码头工程位于东南亚某国家，主要用于集装箱货轮的装卸，适用集装箱船规模为3 500～7 000 TEU。土层大部分为碎石层及砂层，局部为粉土。土层为松散到密实不等，标贯击数主要分布在0～30击，局部含硬夹层(标贯大于30击)。码头所在地地震发生频率高、强度大，设计基本地震加速度峰值为0.53g。出于安全和经济的考虑，工程采用PHC管桩、钢管桩和碎石桩3种方案进行比选。本文选取其中的PHC管桩作为研究对象。

2 计算模型的建立和参数的选用

2.1 动孔压模型

(1)

Byrne[7]提出了一种计算塑性体积应变增量的简便方法：

(2)

式中：Δευd为塑性体积应变增量；ενd为累积体积应变；γ为循环剪应变幅值；C1、C2为相关参数，关系如下：

C2=0.4/C1

(3)

C1与砂土密实度Dr的关系如下：

C1=7 600Dr-2.5

(4)

Byrne模型中还有一个参数C3表示发生塑性体积应变的最小剪应变值。

2.2 模型参数的选取

2.2.1土体参数

土体在x、y和z方向的尺寸均取20 m，沿z方向从上到下分别为0.8 m护坡、17.6 m细砂层和1.6 m砾石层。护坡和砾石层作为不考虑液化层，采用Mohr-Coulomb模型，而细砂层作为液化研究对象，采用Byrne模型。土的力学参数见表1，流体参数及液化参数见表2。考虑该工程的实际情况，水位取在土体上方2.5 m处。

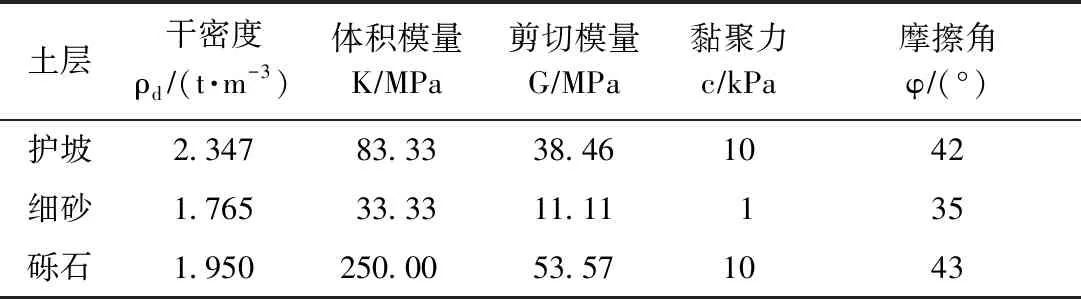
表1 土体力学参数

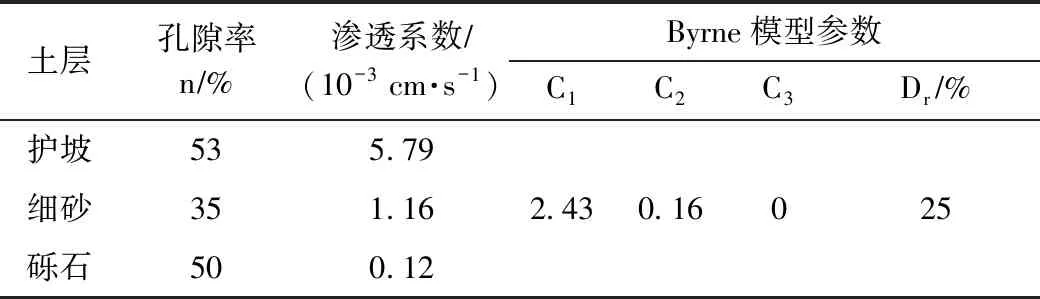
表2 土体流体及液化参数

2.2.2桩参数

采用桩径1 000 mm、壁厚130 mm的A型PHC管桩，桩长24.0 m，伸出土体的高度为4.0 m。桩身混凝土强度等级为C80，弹性模量为38 GPa。采用FLAC3D中的锚索单元模拟PHC管桩中的预应力钢筋，预应力钢棒[8]分布圆直径为880 mm，钢棒直径为10.7 mm，弹性模量为200 GPa，密度为7.86 t/m3。

2.2.3桩-土接触面参数

桩-土接触面参数见表3。

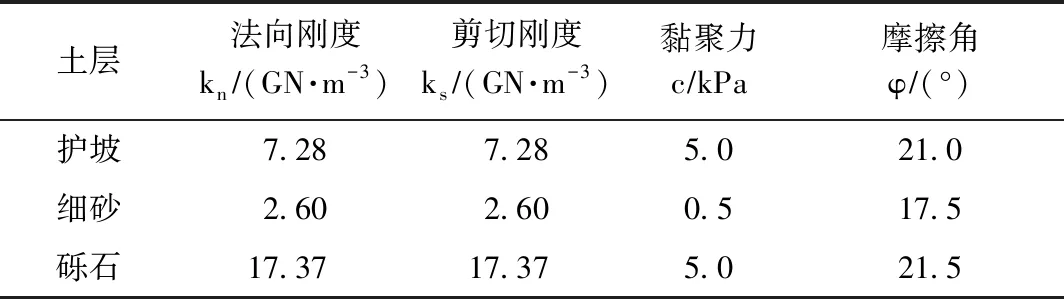
表3 桩-土接触面参数

2.2.4上部结构等效及参数

通过将桩上部结构考虑为作用在桩头上的集中质量，从而将地震荷载下的惯性效应纳入动力模型。模型中在桩顶部建立一个与桩截面形式相同，高度取为1.0 m的圆柱体等效为集中质量，质量取74 t[9]。考虑上部结构材料为C45混凝土，弹性模量为33.5 GPa，密度为96.1 t/m3。由于该集中质量块的密度相较于桩和土的密度较大，直接一次性加载会产生较大的误差，因此桩顶重物的作用通过采用分级加载的方式来实现。

2.3 模型建立

根据设置模型的参数而建立的有限差分模型见图1。

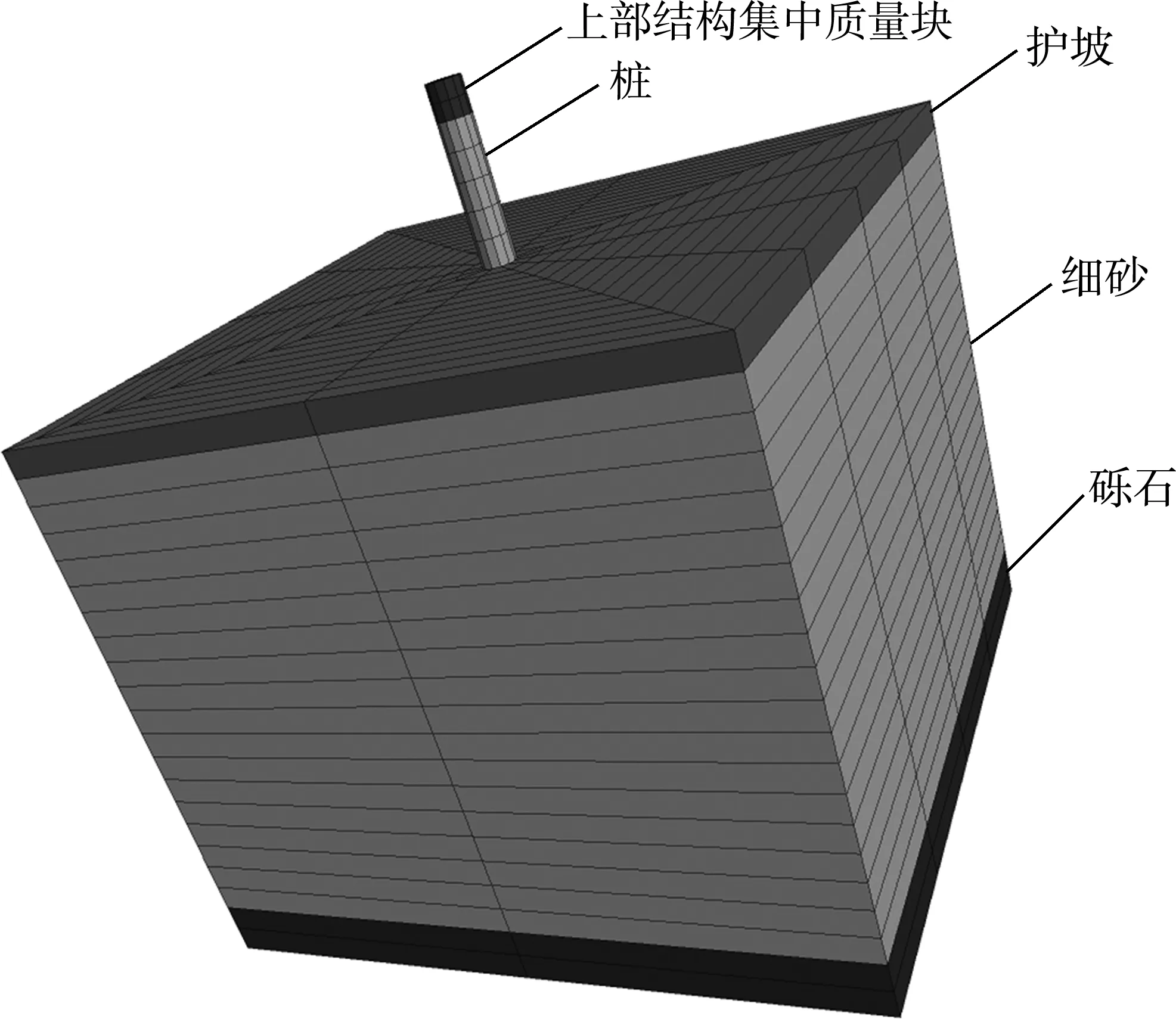
图1 有限差分数值模型

2.4 动力输入条件

采用具有代表性的Kobe地震波并选取其前15 s历程作为动力输入条件，将峰值加速度调至0.53g。调幅后15 s的Kobe波通过快速傅立叶变换转换得到的幅值谱见图2。

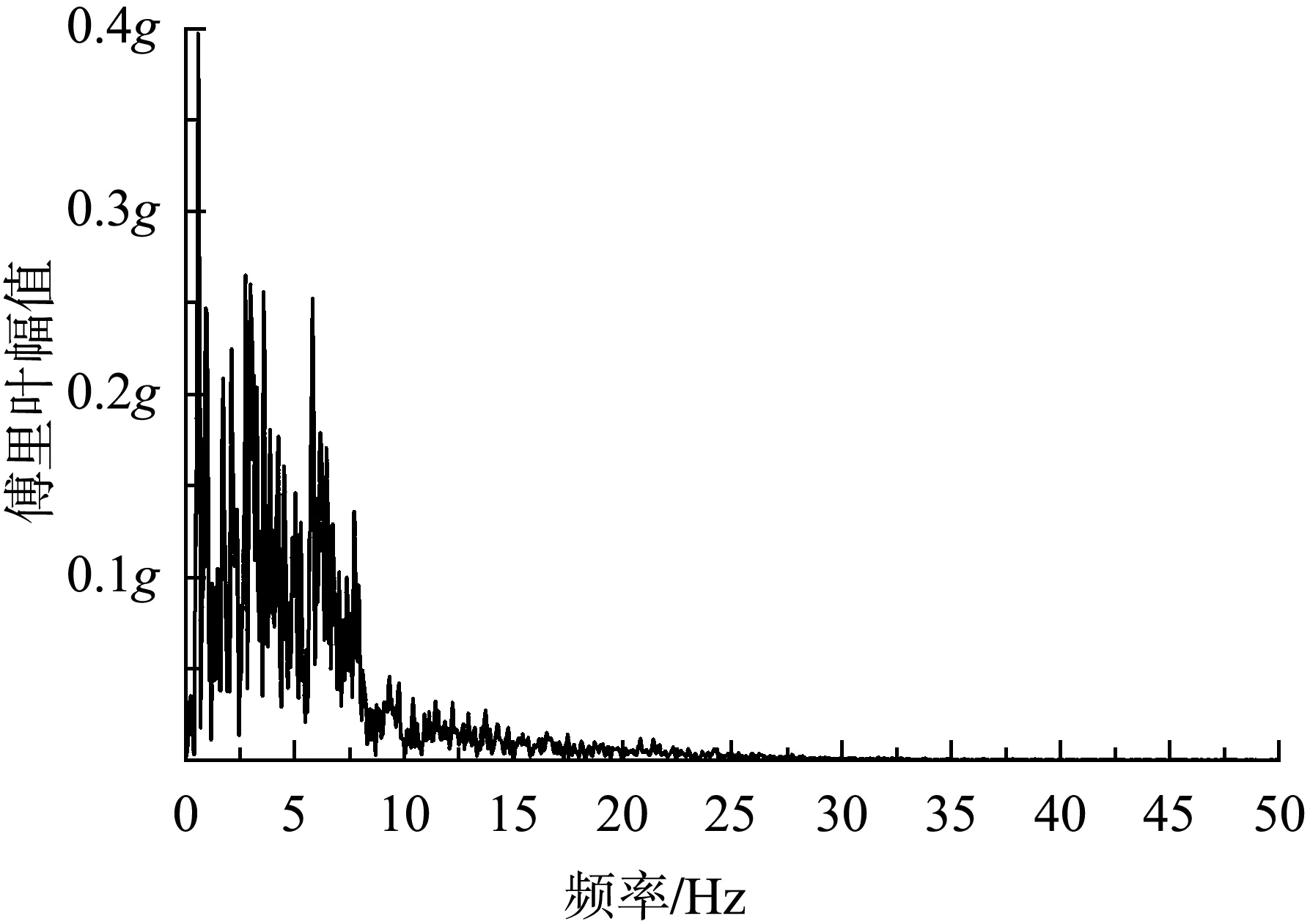
图2 Kobe波傅里叶变换幅值谱

根据Kuhlemeyer和Lysmer研究表明，要想精确描述模型中波的传播，网格尺寸Δl应满足以下关系：

(5)

式中：λ为最高频率对应的波长。

为了尽量增大网格尺寸，从而节约动力计算时间，同时又不降低计算精度，根据地震波的功率谱取地震波最高频率为18 Hz进行滤波，计算得网格最大尺寸为0.8 m。滤波和基线校正均可以通过SeismoSignal软件进行，由软件可得持时为15 s的Kobe地震波最终速度、残余位移分别为-17.368 mm/s、43.128 mm，调整之后分别减小到1.32 mm/s、-7.1μm，因此基本可以忽略最终速度和残余位移的影响。调整后的Kobe波加速度时程曲线见图3。

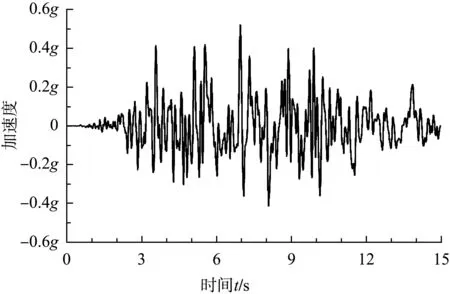
图3 调整后的Kobe波加速度时程曲线

3 结果分析

3.1 土的动力响应和液化判断

3.1.1土的动力响应

本文在细砂层中共选取了坐标分别为(4,0,-6.0)、(4,0,-10.0)、(4,0,-12.5)、(4,0,-15.0)和(4,0,-17.5)的5个监测点(点1～5)进行土的动力分析。点1和5的有效应力与超静孔压时程曲线见图4。

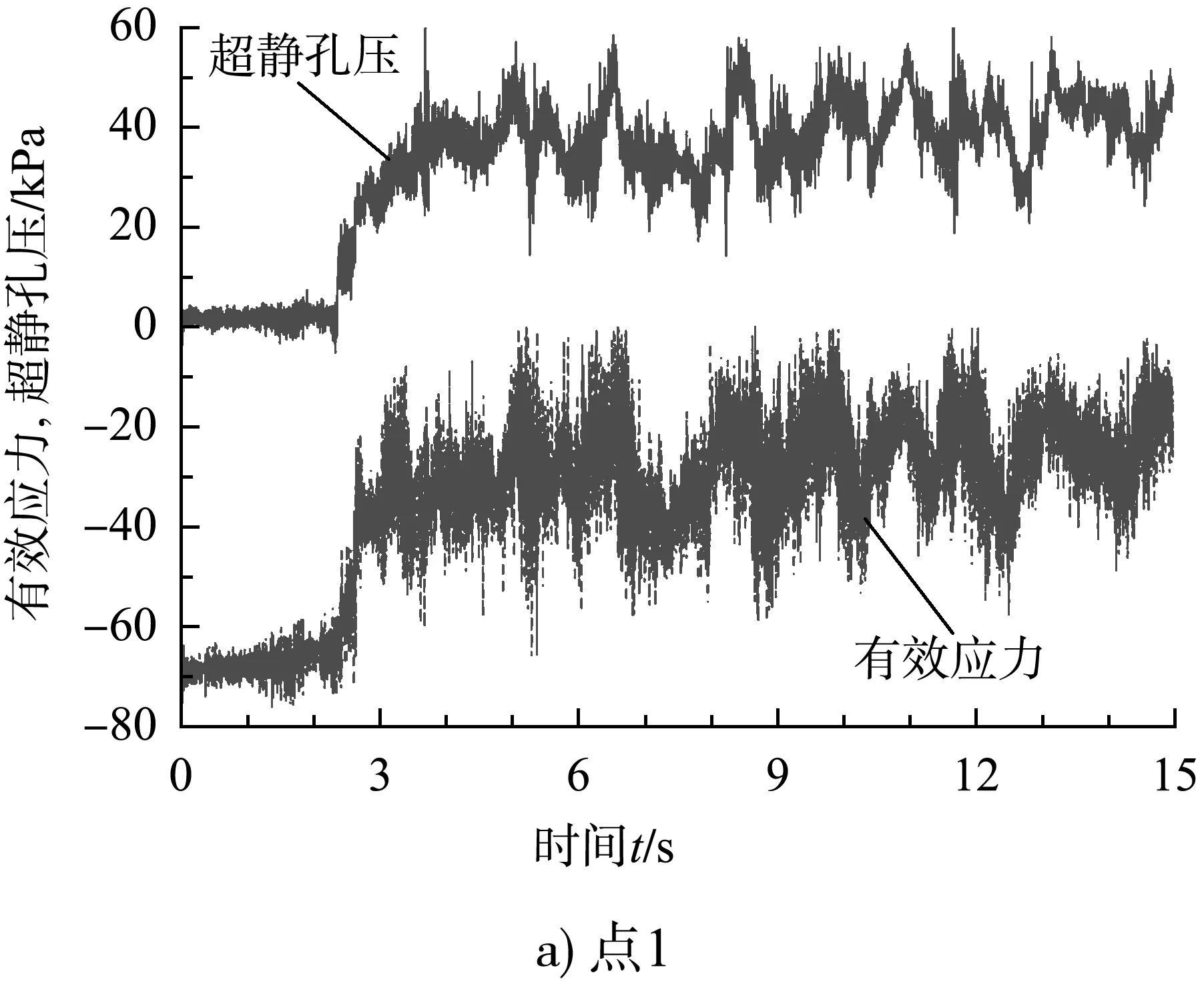
图4 点1和5的有效应力和超静孔压时程曲线

从图4可以看出点1和5的超静孔压的变化情况与地震荷载的变化情况息息相关，地震作用初期有效应力随着时间逐渐减小，而超静孔压则随着时间逐渐增大；后期两者均保持一稳定幅值。点1的有效应力和超静孔压的的首次显著变化发生在3 s之前地震加速度开始显著增大时。点1在3～4 s的历时中有效应力由-70 kPa突变至-20 kPa，超静孔压在3.0～4.5 s的历时中由0逐渐增加到40 kPa。在7、10和12 s左右时，点1的有效应力有一定幅度的增大，超静孔压则相应减小，原因是点1与地表面距离较小，在7 s左右时由于逐渐增大的孔隙水压力超过上覆土层强度，地下水挟带粉粒、砂粒冲破上覆土层发生喷水冒砂现象，孔隙水压力逐渐消散。7 s时有效应力下降段之后伴随着增大段，主要是由于上覆土层有效应力下降的过程在竖向上相当于卸荷的过程，受压缩的土体发生塑性回弹，土体因排水强度提高而发生有效应力增大。总体而言5 s之后，有效应力和超静孔压均保持一定幅值而不断振荡变化。

点5的有效应力和超静孔压的变化规律与点1大致相同，不同之处在于点5的首次突变发生时间相较于点1出现了滞后；点5液化之后的有效应力始终保持在-35 kPa的较低水平附近，有效应力和超静孔压发生振荡的幅度较点1小。原因是点5较点1埋深大，上覆土层强度大，有效应力大，消散程度相较于点1更慢，同时发生液化之后增大的孔压未达到较大的上覆土层强度而没有发生喷水冒砂现象，因此振荡的幅度也较小。

3.1.2场地变形分析

图5为地震荷载作用前后的模型网格变形对比，可以看出模型变形主要发生在上部护坡层和砂土层，底部砂土、砾石层的网格几乎没有变形。砂土层的网格由桩向外变形逐渐增大，远离桩的土体几乎不受桩-土相互作用的影响，承担全部地震荷载的作用，因刚度较小而导致较大变形。

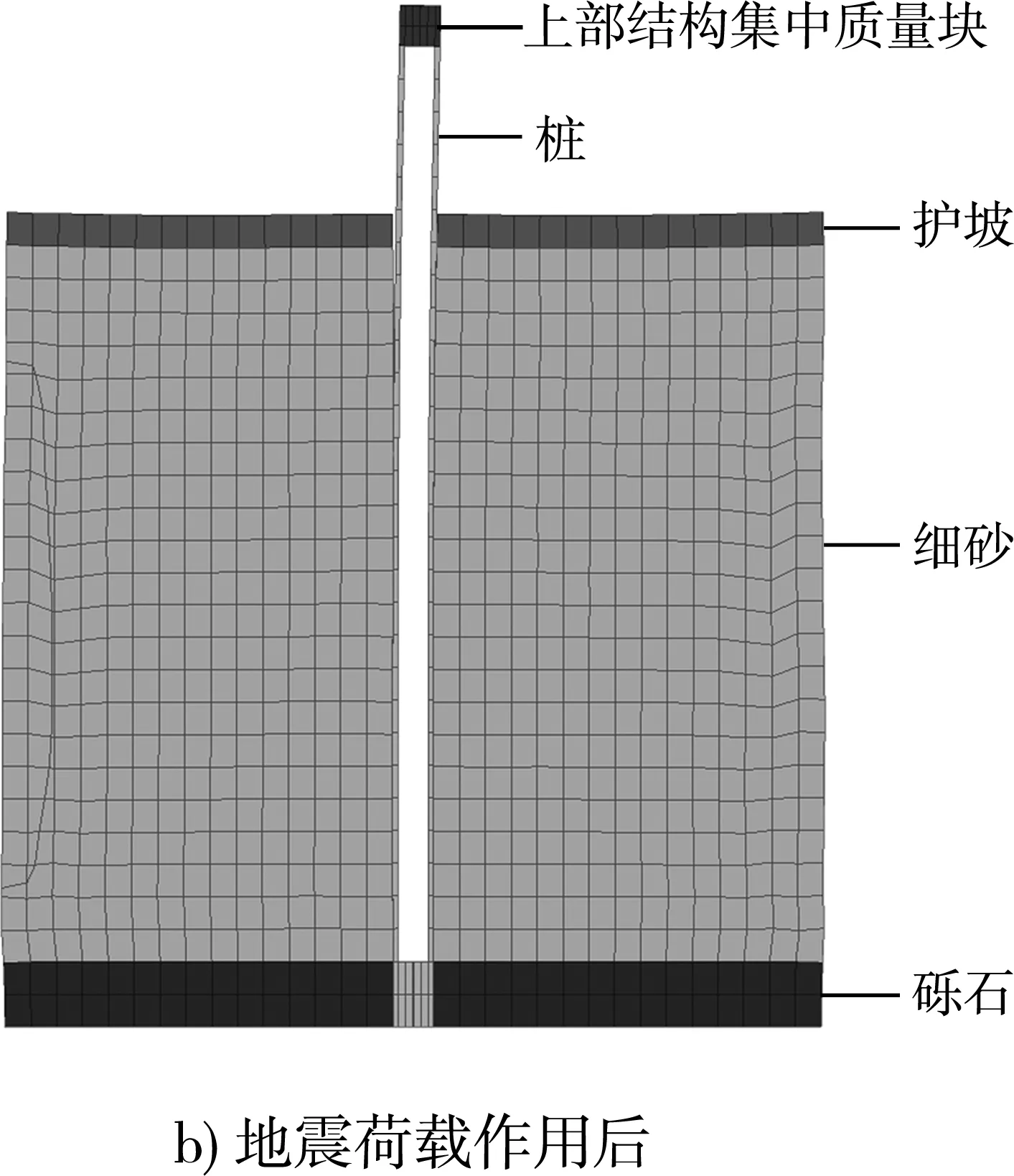
图5 地震荷载作用前后模型网格变形对比

分别取z为0、-3.5、-6.0、-9.0、-12.5、-15.0、-17.5和-20.0 m(水平坐标均为x=5.0 m，y=0 m)处的土体位移作为研究对象。特征时刻与特征高度处的土体侧向位移曲线见图6、7。由t=3 s时的曲线可知，在地震作用初期，地震荷载水平较弱，土体尚未发生液化现象，土体的侧向位移趋近于0，各个深度处的土体位移相同。随着地震作用的增强，液化由上而下逐渐发展，不同深度的土体也开始出现位移差，位移差逐渐增大。8个监测点处的最大位移发生在z=-3.5 m处，z=0 m处的土体位移相较于其余7点处相差不大，这两个监测点均靠近护坡和砂土层交界处，可以得出土体最大侧向位移发生在上部土层交界处附近。由图7中5个位置处土体的位移历时曲线可以得出土体侧向位移上部整体大于下部，从上至下呈先增大后减小的变化趋势。地震作用结束时(t=15.0 s)护坡层和细砂层上部的位移仍然较大，埋深超过6.0 m的土体位移均趋近于0，与图5网格的变形规律相一致。

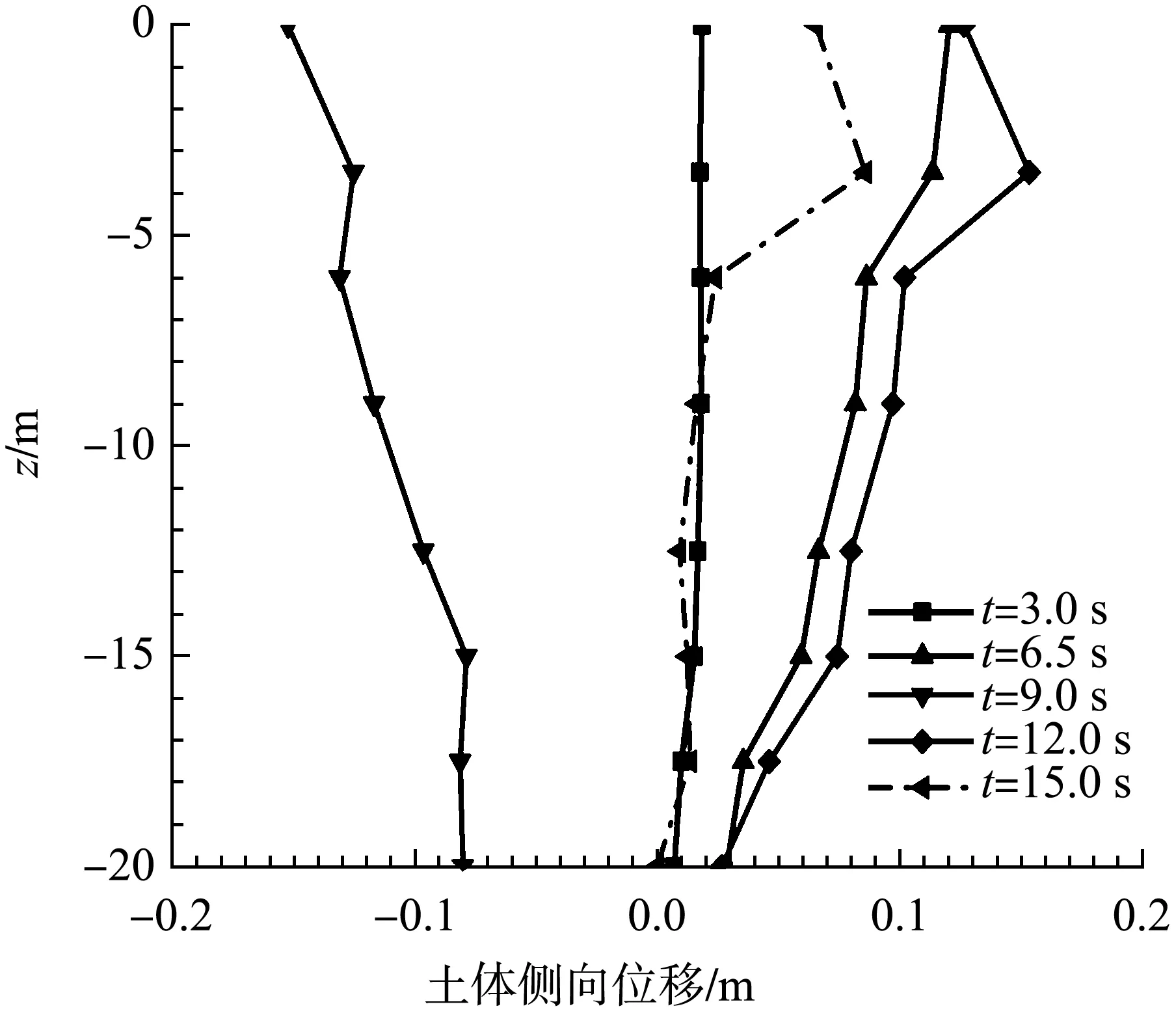
图6 特征时刻土体侧向位移曲线

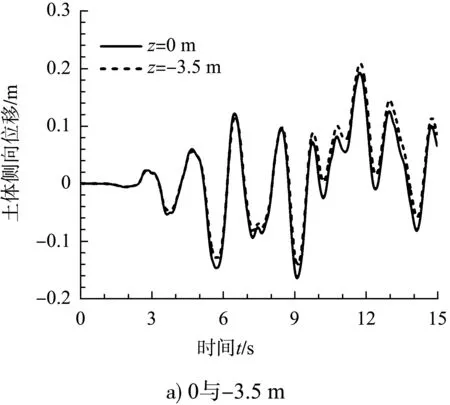
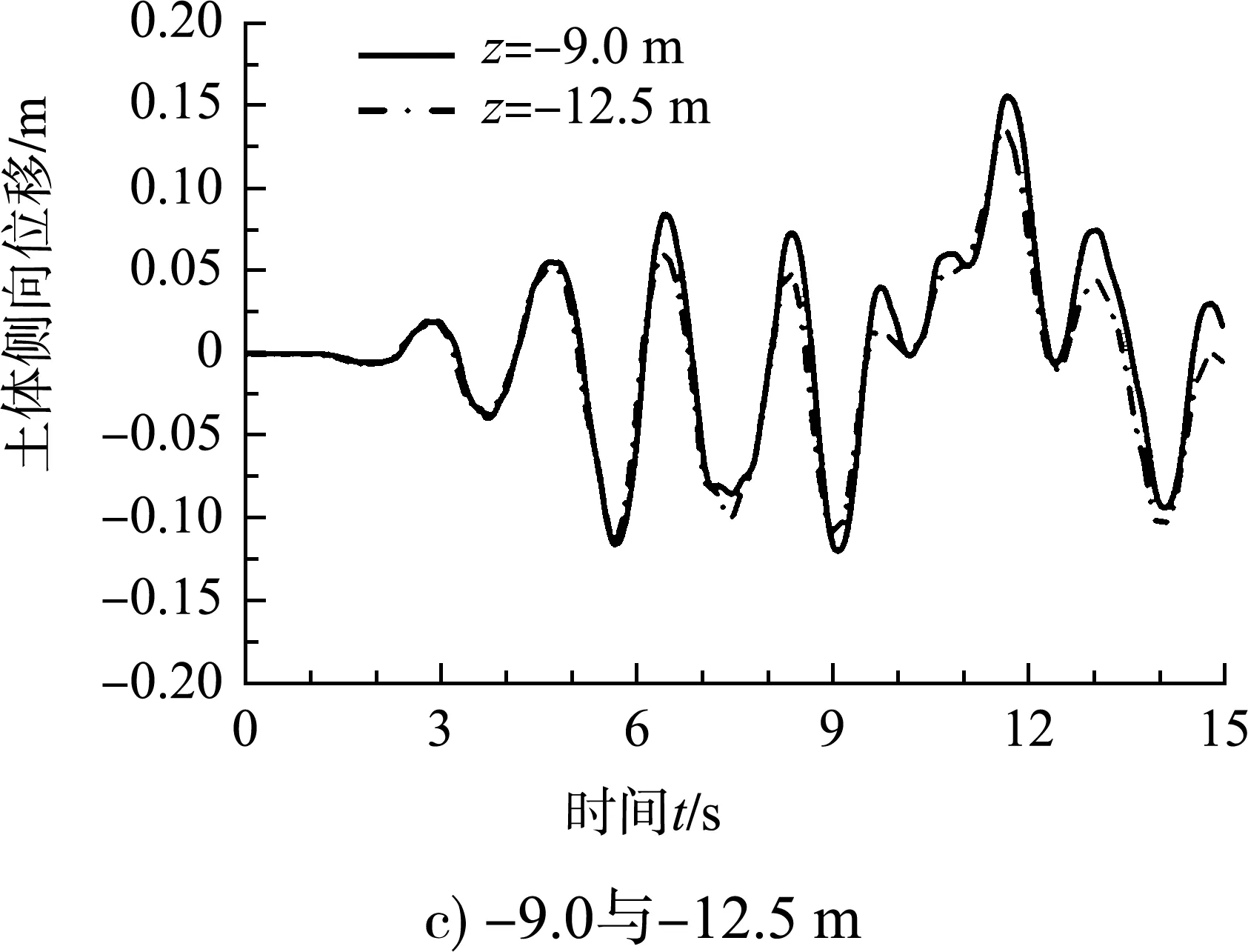
图7 特征高度处土体侧向位移曲线

3.1.3砂土液化的判别

地震动荷载作用下地基产生超静孔隙水压力，超静孔隙水压力导致有效应力的减少，当孔隙水压力等于总应力时地基有效应力等于零，这时地基完全丧失了承载能力，对上部结构产生极大的破坏。超静孔隙水压力的产生取决于地基土的材料性质，对于砂土地基地震作用下极易产生超静孔压，而孔压不容易消散，当孔压达到一定程度时即发生砂土地基液化[10]。在仿真计算中常用超静孔压比的概念来描述液化，超静孔压比Ru的定义为：

Ru=1-σ′m/σ′m0

(6)

式中：σ′m为动力计算过程中单元的平均有效应力；σ′m0为动力计算前单元的平均有效应力。

在振动作用下，一般认为超孔压比达到0.8左右时，土体产生初始液化，到达1.0时，土体达到完全液化。

图8为点1和5的超静孔压比Ru时程曲线。超静孔压比Ru时程曲线变化规律和有效应力的变化规律一致。地震作用初期，输入地震加速度幅值不超过0.05g，砂土未发生液化；2.5 s后输入地震加速度幅值开始超过0.1g；3.2 s之后输入地震加速度幅值均保持在0.2g以上的水平。在3.2 s时点1超静孔压比Ru首次达到80%，即认为深度为6 m的细砂土在3.2 s时开始发生液化，点5的超静孔压比Ru首次达到80%发生在5.5 s左右，深度为17.5 m的细砂土在5.5 s左右开始发生液化，表明液化的发生与否以及开始发生的时间与土体埋深和地震加速度序列及峰值加速度均有关联。点5处砂土的有效应力在液化之后一直保持在较低水平，超静孔压比Ru始终保持在80%左右，埋深为17.5 m的点5液化的持续时间相较于埋深为6 m的点1长。由于点5处土体深度接近砂土深度最大处，因此可以认为该模型细砂土全深度均发生了液化。

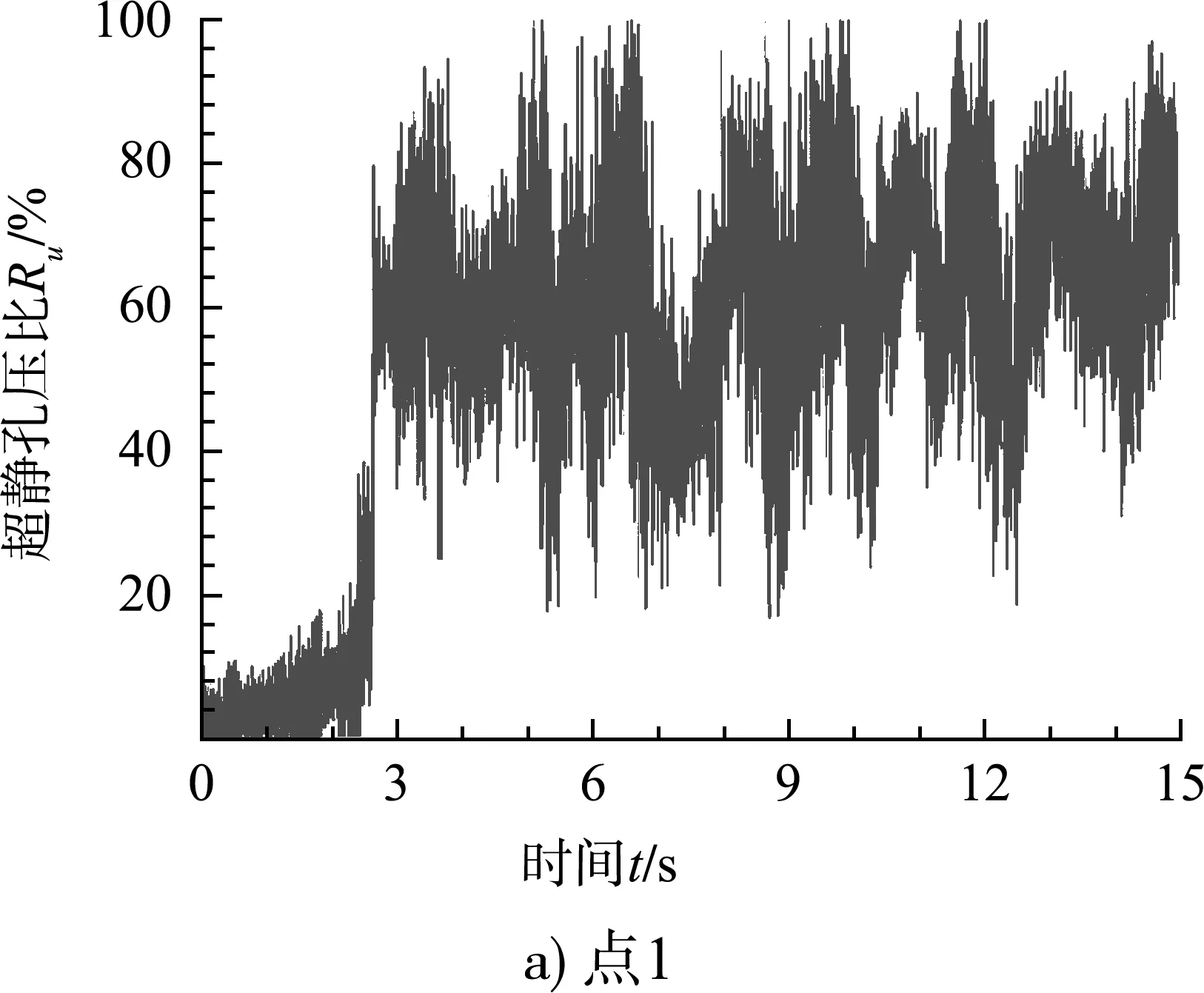
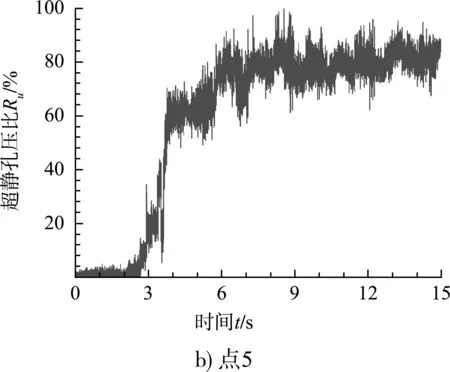
图8 点1和5的超静孔压比Ru时程曲线

3.2 桩身内力响应

由于本文利用FLAC3D建立PHC管桩模型时采用的是实体模型而非桩单元，不能直接得出桩身弯矩，所以此处进行的桩身内力响应的研究对象是桩身正应力Szz。分别取z为3.5、2.0、0、-2.0、-5.0、-9.0、-12.5、-15.0、-17.5 m(水平坐标均为x=0.47 m、y=0 m)处的桩身正应力作为研究对象。图9为特征时刻处的桩身正应力曲线，图10为特征高度处的桩身正应力曲线。地震作用前3.0 s桩身正应力较小，主要由于此时土体液化现象仅发生在细砂层埋深较浅的地方，桩周土仍然具有一定的侧向承载力。随着液化程度的发展，液化深度逐渐增加，丧失侧向承载力的土体区域不断扩大，桩身正应力不断增加。桩身正应力从上至下呈先增大后减小的变化趋势，最大桩身正应力出现大致在护坡和细砂土交界处并且呈向下移动的趋势。

图9 特征时刻处桩身正应力曲线

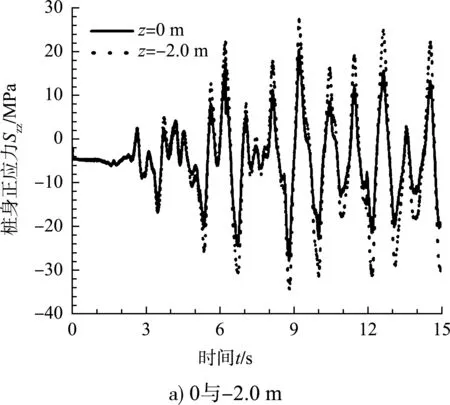
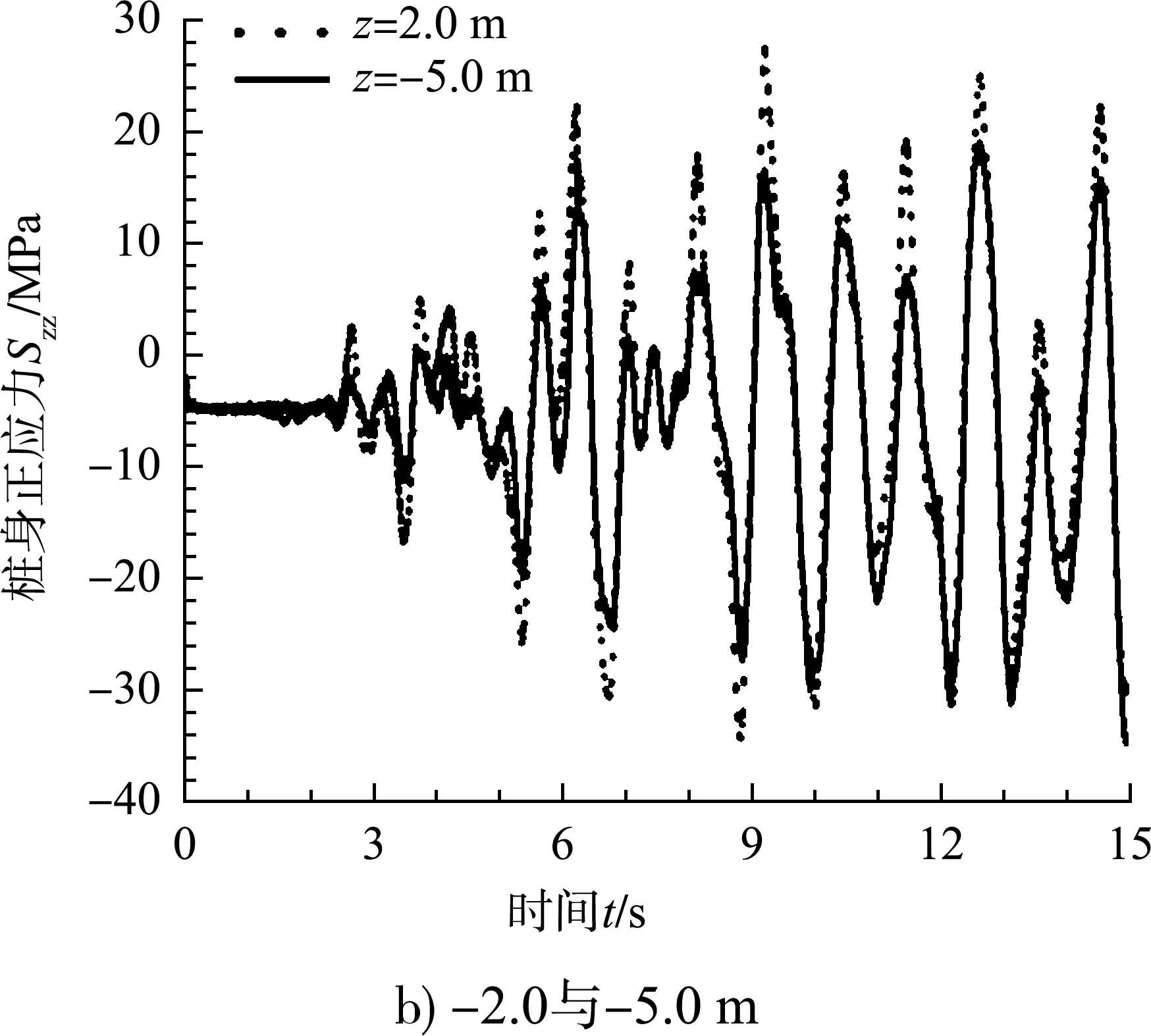
图10 特征高度处桩身正应力曲线

3.3 桩变形分析

分别取z为3.5、2.0、0、-3.5、-6.0、-9.0、-12.5、-15.0、-17.5 m(水平坐标均为x=0.47 m、y=0 m)处的桩身位移作为研究对象。图11为特征时刻和特征深度处桩身侧向位移曲线。由t=3.0 s时的曲线可知：地震作用初始时刻，振动幅度较小，桩的侧向位移较小。随着地震振动幅度的增大，土体开始出现液化，埋深较浅处的桩的侧向位移明显增大，未发生液化部分的土体仍然承受一定的地震作用，桩产生的位移较小。随着液化的发展桩承受地震的作用比例越来越大，桩身位移逐渐增大。在土体以上的桩身侧向位移变化相差很小；埋入土体的桩身由于开始发生液化的时间不同，液化发生较早的、埋深较浅处的桩比液化发生较晚、埋深较大处的桩侧向位移大。桩身侧向位移总体上由上至下逐渐减小，最大值出现在桩顶处。由于地震强度较大，桩顶水平位移在t为6.0、9.0 s左右均超过了《建筑桩基技术规范》[11]中规定的桩顶允许水平位移，结构处于危险状态，一方面可以通过加强桩顶截面刚度，另一方面可以通过改善土体性质，降低土体液化程度和范围来满足抗震要求。

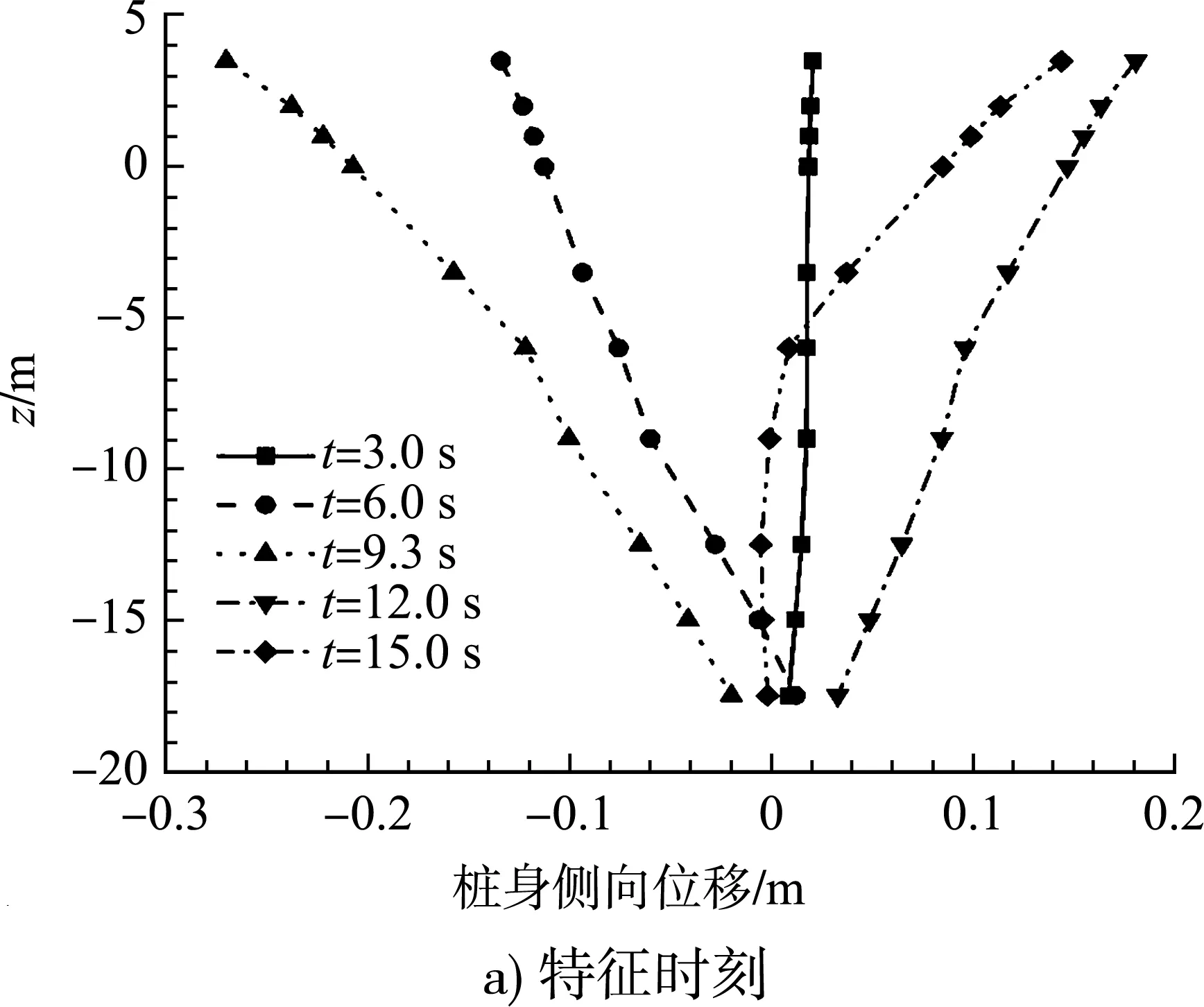
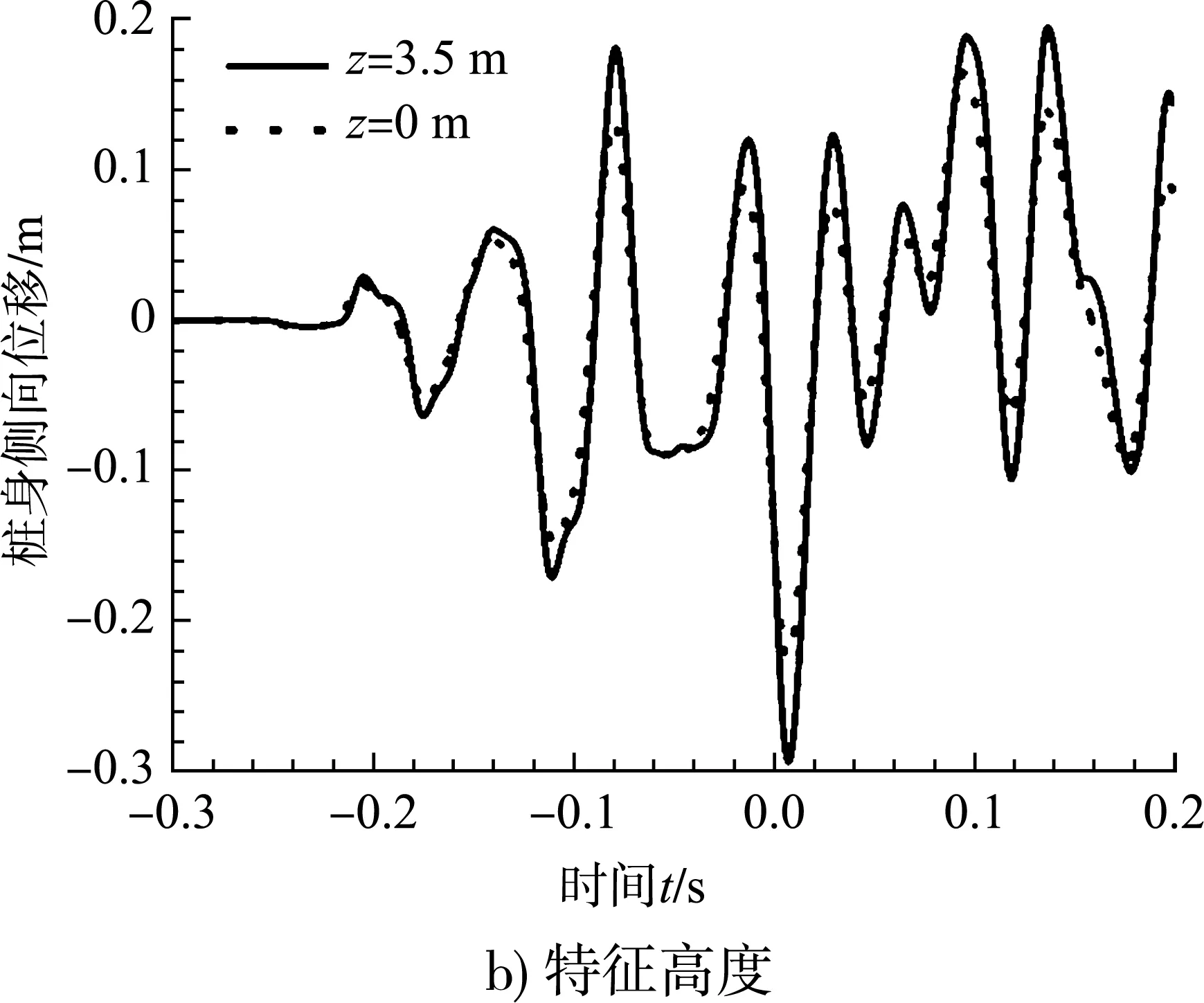
图11 桩身侧向位移曲线

4 结论

1)地震作用引起模拟的埋深较浅的砂土孔隙水压力急剧增大，有效应力急剧减小，超静孔压比趋于1.0，砂土发生液化。随着地震作用的增强，液化区域逐渐下移发展，最终全高度砂土均发生液化。砂土液化的发生与否以及液化开始发生的时间不仅仅与土体的埋深有关，也与地震荷载的峰值加速度相关。

2)桩身正应力随着液化的发生和发展而不断增加，液化高度内的桩身正应力从上至下逐渐减小，最大桩身正应力出现在护坡和细砂土交界处。桩身侧向位移随地震强度的增大逐渐增大。在液化发生较早的、埋深较浅处的桩的侧向位移大于液化发生较晚的、埋深较大处。

3)由于该地区设计地震强度高，PHC管桩在强震作用下的位移和内力值均较大，直接应用PHC管桩于该实际工程显然是不合适的，需要在码头建造之前对该易液化的场地进行改善，必要时可采用钢管桩。