不同时间间隔的波浪观测数据对其统计结果的影响*

陆卓翔，乔光全

(中交第四航务工程勘察设计院有限公司，广东 广州 510230)

由于波浪观测工作受当地海区自然条件和观测条件限制，观测方法的不同导致获取的波浪数据的时间间隔不一，分析不同时间间隔的波浪数据对其统计结果的影响是十分必要的。人工观测是海洋站和早期观测获取波浪数据最主要的方法[1]；随着观测技术的发展由仪器代替了人工观测[2]，但由于以前电池续航短导致仪器获取观测数据的间隔较长，直至现代，才得到时间间隔较短的观测数据。

工程设计中，对工程海域波况进行分析，通常使用的是海洋站一年或多年的实测资料，或使用测波仪器获取海域的逐时一年的观测数据；对于设计波浪通常使用的是台风浪数值后报或海洋站的长期观测资料。在工程设计前期，通常使用规范[3]推荐的设计波浪，而规范中的设计波浪是用海洋站的长期观测统计出来的设计波浪值，这些数据多由人工观测获取，这种方法通常是在白天进行且时间间隔较长。通过分析不同时间间隔的波浪数据得到不同的统计特征，它们之间的一致性和差异性将影响工程设计波浪要素的取值，因此对上述一致性和差异性的探讨分析是十分必要的，本文根据大埕湾的实测波浪，分析3种不同时间间隔对波浪统计成果的影响。

1 实测数据来源

实测数据采用2017年3月1日—2018年2月28日连续1年，在潮州大埕湾近岸测波点(W1)得到的定点每小时连续测波资料[4]。观测位置见图1，测点处实测水深为12.6 m。观测采用的仪器为DATAWELL MARK Ⅲ型波浪骑士测波浮标，该仪器属于重力式测波仪，是荷兰DATAWELL公司生产的波浪测量仪器，测量精度和准确度高，是当今世界上最好的海洋测波仪器之一。经仪器自带软件处理后，可统计得出每30 min的波高、周期特征值及波向等数据[5]。岸站接收仪可实时接收数据，并监控测波仪器状态。

图1 波浪测站位置

2 数据分析方法

为避免不同观测仪器或人员本身的目测误差，获取的波浪资料均出自同一组观测数据。对逐时观测资料依据不同的时间间隔分别截取数据1和数据2，测量数据为近代测波仪的原数据，截取的数据1和2分别代表早期测波仪和人工目测法数据。不同的数据序列提取时段见表1。

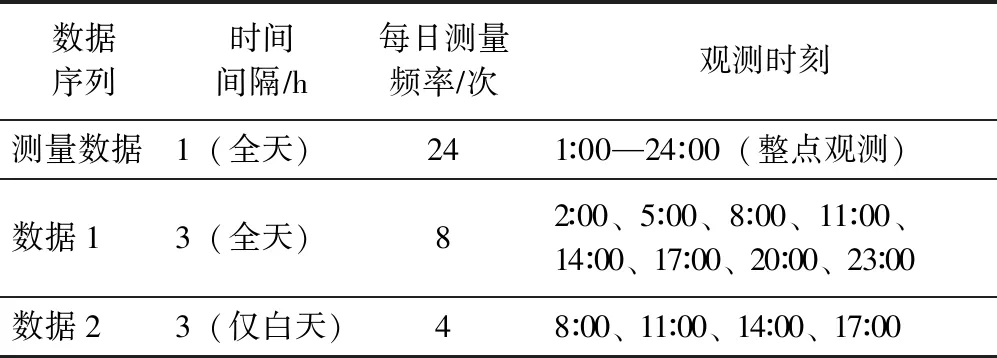
表1 不同的波浪数据类别测波间隔时间

在3组数据中分别提取20组产生最大波高的连续波列进行最大有效波高及对应的波周期进行分析，对比不同时间间隔下波向和波浪特征值的差异。

3 结果分析

3.1 波况分析

数据1和2的波况和波浪玫瑰图见表2和图2。可以看出，本海区全年波浪方向集中在SE(常浪向)、ESE(次常浪向)、SSE和 S 方向，这4个方向波浪的年分布频率分别为 48.11%、19.59%、15.89%和 15.51%，占全年波浪的 99.09%。受西南侧南澳岛及西北面大陆的掩蔽影响，SSW-W-N 向浪仅占全年的 0.68%，东侧由于东山岛屿的阻碍，N-E向浪也较少，仅占全年的 0.23%。

根据表2可以看出，3种不同的时间间隔统计出来的波向频率基本相同，各波向频率统计差异不到1%，平均波高均是45 cm，因此都能较好地反映测量海区的波浪分布情况，所以数据1和2的统计结果，仍能较好地代表当地实际波况。

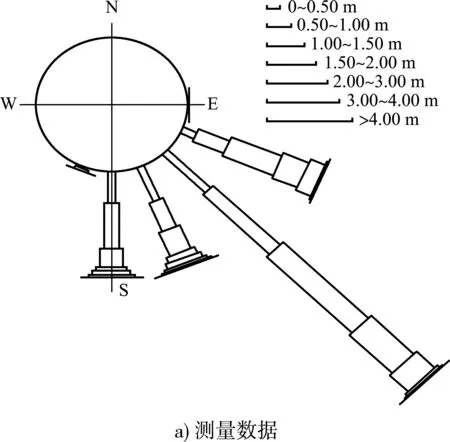
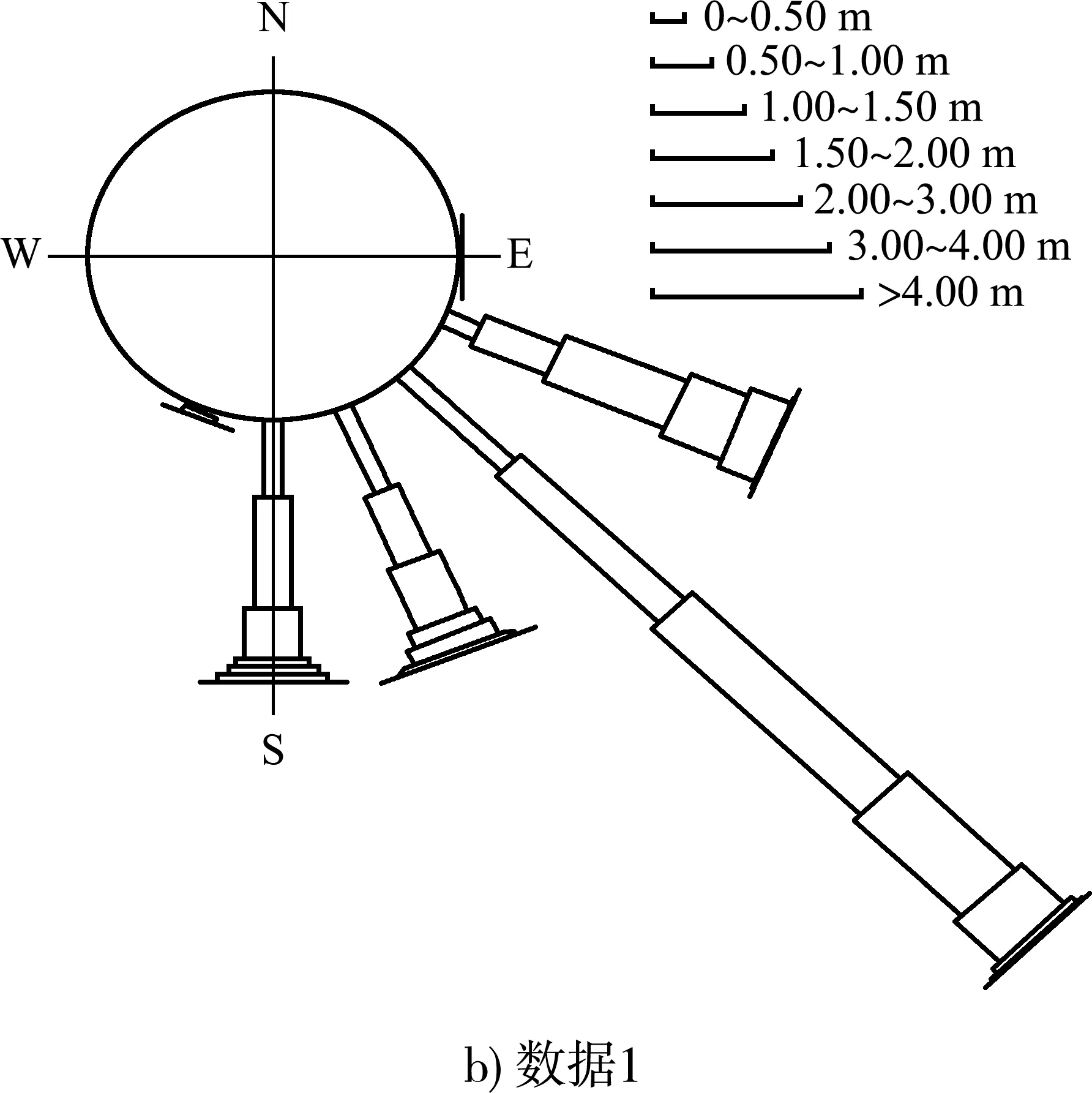
图2波浪玫瑰图

表2 不同数据序列的波况

3.2 数据统计

从2017年3月1日—2018年2月28日的波浪观测数据中，根据波浪大小挑选20个最大的连续波统计分析3组数据的最大有效波高和对应的波周期，并分析其差别。

3.2.1大浪的有效波高

表3为测量数据与数据1、2之间最大有效波高的对比。可以看出，测量数据与数据1之间最大波高相差28 cm，最大相对误差为11.4%，平均值相差3.6 cm，平均相对误差为1.6%；测量数据与数据2之间最大波高相差28 cm，最大相对误差为9%，平均值相差10 cm，平均相对误差为5%。

表3 测量数据与数据1、2的最大有效波高对比

续表3

编号测量数据最大有效波高∕cm数据1数据2最大有效波高∕cm绝对误差∕cm相对误差∕%最大有效波高∕cm绝对误差∕cm相对误差∕%1021721700199188.3112042040019683.91219819621.019263.01319619242.0185115.61419218931.6182105.21518918542.118094.81618818263.2178105.31718518052.717694.91817917810.617273.919171176-5-2.9159127.020158176-18-11.415800最大值32732728-11.4327289.0平均值218.9215.33.61.6208.110.95.0

3.2.2波周期

表4为最大有效波高对应的波周期。可以看出，测量数据与数据1的最大波周期差为4.5 s，最大相对误差为54.9%，平均值为0.37 s，平均相对误差4.4%；测量数据与数据2的最大波周期差为3.2 s，最大相对误差为78.1%，平均值为0.24 s，平均相对误差2.8%。

表4 测量数据与数据1、2的有效波周期对比

3.3 相关性分析

3.3.1大浪的有效波高

数据1和2有效波高的线性拟合图见图3。可以看出，数据1与测量数据有效波高的相关系数R为0.980 7，具有较好的相关性；数据2与测量数据有效波高的相关系数R为0.984 9，具有较强的相关性。时间间隔较长的波高可由图中的两个拟合公式进行计算得出。

图3 数据1和2有效波高的线性拟合

3.3.2大浪的有效波周期

数据1和2有效波周期的线性拟合图见图4。可以看出，数据1与实测数据有效波周期的相关系数R为0.507 1；数据2与实测数据有效波周期的相关系数R为0.619 9。结果表明，数据1、2与实测数据有效波周期的相关性较差。

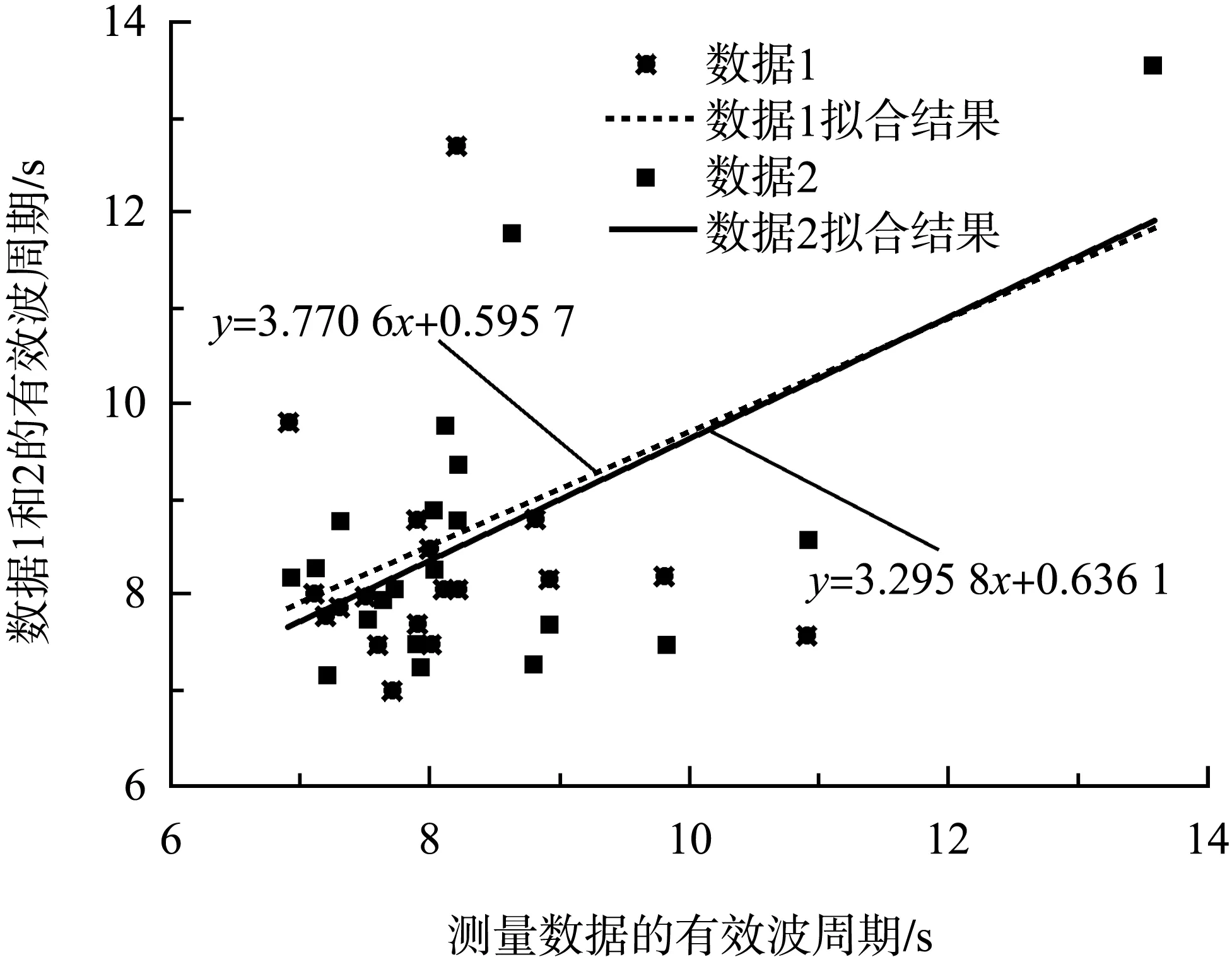
图4 数据1和2有效波周期的线性拟合

综上所述，不同时间间隔的波浪观测资料的波高差异较小，大浪波高差异在11.4%以内，相关性较好；但波周期相差较大，大浪的有效波周期差异在78.1%以内，相关性较差。

4 结论

1)3种不同时间间隔的波浪数据都能反映测量海域的全年波况。

2)数据1和2的最大有效波高与观测数据的相关性较好，可以用线性拟合公式进行换算，得到的波高值具有较高的精确度。

3)不同时间间隔数据的波浪周期的线性相关性差，但最大有效周期的平均值相差不大。

4)本文的3种观测波浪的方法并不是针对观测方法不同而比较，是比较时间间隔不同的波浪观测数据，对波高、波周期等进行分析，但是因为观测站点具有一定局限性，仅适合被测量的海域，对于其他海域位置的不同时间间隔的波浪数据的关系需要做进一步分析。