上承式拱桥立柱在超速汽车下的动态效应

吴隆 李海涛 王彦文

摘要：为了分析上承式拱桥立柱在移动荷载下的车一桥耦合效应，在考虑拱肋的内力的前提下通过理论分析，利用有限元方法建立起拱桥、车辆的模型，通过试验监测数据和数值分析结果分析汽车的超速现象对桥梁立柱应力、位移及桥梁变形的影响。结果表明车辆的超速行驶对立柱的轴力产生明显的影响，立柱在z方向剪力会产生应力峰值，同时超速现象对立柱y方向剪力及桥梁的变形并没有直接影响。

关键词：桥梁工程;拱桥;立柱;有限元方法;拱肋内力;超速

中图分类号：U448.2

文献标志码：A

文章编号：1672-1098（ 2020）04-0076-07

作者简介：吴隆（1996 -），男，安徽黄山人，在读硕士，研究方向：桥梁工程。

拱桥作为一种特殊且常见的桥梁形式，由于其特殊形式及特殊受力形式，众多学者对其在各种荷载作用下的动力响应及损伤做了很多研究。Sher-van Ataei[1]等通过对动态放大系数（ DAF）的分析计算，研究了使用寿命较长的石拱桥在不同轴载列车作用下的动态响应。M.R.Akbari[2]等用竖向简谐荷载作用下的拱形梁对拱桥的非线性振动进行了建模和仿真，并通过Akbari-ganji method（ AGM）对其进行了分析，研究而拱形梁的非线性振动特性。Vicente N.Moreira[3]等运用塑性理论，分析了葡萄牙的5座建成年代较久的石拱桥承受高于所设想的动态荷载下的承載情况和可用性性能。H-Gonen[4]等研究了帕鲁桥在恒载下的变形和应力，同时将地震加速度作为荷载对该桥进行了数学建模及动力分析和计算。Abdulkadir Cnneyt Aydin[5]等研究了奥杜省的萨普戴尔桥在一定荷载作用下的受力性能和在不同位置受到荷载作用下的性能。

由于车辆性能的不断改进及驾驶人员的疏忽，车辆超速行驶现象已屡见不鲜。基于此其现象，本文对中国贵州省福泉市三江口拱桥考虑在受到相应弯矩、轴力和剪力的作用下，在移动荷载作用下立柱的车一桥耦合效应进行了理论分析、模拟和试验，研究了立柱在超载和超速下的动态响应。

1 工况描述

本桥位于中国贵州省福泉市三江口镇，修建于1986年，主拱圈结构为双曲拱桥，桥面宽度0.82+7.0+0.82m，主跨径55.0m，矢高6.85m，主拱圈由4根拱肋组成，拱肋截面高度70cm、宽度60cm，两端分别有简支梁混凝土引桥，设计时速30km/h。本桥在设计时主拱圈采用悬链线作为拱轴线，拱轴系数m=1.988。

2 车一桥耦合系统（VBCV）

目前，数值分析方法因为其较低的限制性和较低的花费被大量用于分析VBCV问题[6]，而且有文献验证了数值分析方法与试验结果能较好地吻合[7-8]，对于车桥组合结构，通常采用Newmark和Runge—Kutta法来正确的解决耦合振动[9]。

本文运用叠加方法解决VBCV问题，首先分别建立车辆和桥梁的方程，并通过边界条件将两个子系统进行组合叠加，在不同情况进行分析得到相应的动态响应。

2.1 车辆模型

采用经典三轴车辆模型，该车总质量30t，将车辆划分成一个车体质量，6个车轮及悬挂质量。用弹簧一阻尼系统模拟车体一车轮和车轮一桥面之间的联系，从而将车辆模型简化成质量、弹簧、阻尼系统所组成的三维有限元模型体系[10]。其中M为车体质量;m1～m6为车轮及悬挂质量;kt1～kt6ct1～ct6为悬挂的刚度和阻尼;ks1～ks6、cs1一cs6为轮胎的刚度和阻尼。同时还考虑了车轮竖向位移z1～z6、车体竖向位移zv、车体横向及纵向转动位移θv、φv，共9个自由度。

2.2 桥梁模型

对于本桥梁拱肋部分采用虚拟梁单元和实体单元拼接而成，左右两侧立柱采用梁单元，中间部分用梁单元模拟填料，桥面板用板单元模拟，根据施工图建立三维有限元模型（见图1），其中行车方向为x方向，图示方向右为正;横向为y方向，图示方向左上方为正;竖向为z方向图示方向上为正，图1左下方符号处为原点。

2.3车一桥组合系统

1）车辆模拟

对于三轴车辆，建立起三轴车辆模型[11]并根据D' Alenmber原理，建立起动力学方程

由于在空腹时拱桥中，由于集中力的存在，使得拱的恒载压力线为一条在集中力作用点处有转折的曲线，而不是悬链线，甚至不是一条光滑的曲线[14]。所以在拱肋内会产生弯矩和剪力。

通过查询并计算在考虑弹性压缩影响下拱肋任意截面的内力，则任意截面的偏离弯矩为

3 试验及数值分析

由于试验条件的限制和花费，很难通过监测得到完整的试验数据，故部分结果需要通过数值分析的方法得到。

3.1测点布置

根据本文的目的，在试验中布置测点对桥梁立柱受到的应力及位移进行监测，测点布置于立柱与拱肋相交处，如图2和图3所示。

3.2 试验数据

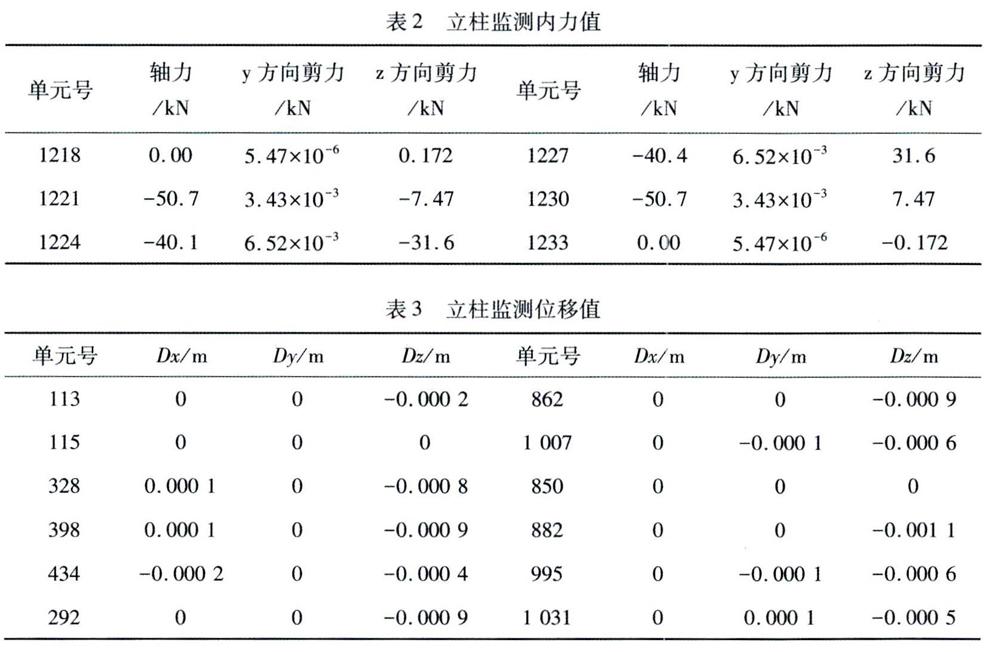
在图1中，选用每排的立柱及测点两侧实体单元作为研究对象，数值模拟中单元号如表1所示。监测所得位移值及内力值如表2和表3所示（均用数值模拟中单元号代替）。

3.3数值分析结果

对桥梁先进行整体分析，得到立柱的内力及位移值如表4和表5所示。对比表2-表5数值可以发现，内力及位移的数值模拟的结果相较于现场监测相差并不是太大，故本文将将数值模拟所得到的结果作为试验值进行分析。

1）动力特性

根据桥梁的材料、刚度、几何尺寸等条件得到桥梁的前四阶振型如图4所示。

2）车辆匀速前进时立柱的动态响应

由表3和表4可知，同一排3根立柱各值差异不大，现选用中间立柱作为研究对象。为了对比六立柱在汽车不同行驶速度下的动力响应，设计时速分别为20km/h和30km/h的车辆匀速通过桥，测量6根立柱在两种情况下的轴力、剪力及变形，由表格形式列出。

通过对比表6、表7可以发现，在未超过设计时速时，随着车速的增大，轴力及z方向剪力最大值有少量增加，由于车辆对称作用，y方向剪力几乎等于零。在变形方面，在x方向有少量变化，y方向和z方向几乎没有变形，故在为超速时，速度对变形影响不大。

3.4 超速下车一桥耦合现象

由于现在车辆大多都是超速行驶，故本小节研究在超速情况下立柱的响应。

设置汽车分别以40km/h、50km/h的速度匀速通过桥梁，对其进行模拟，可以得到六根立柱在超速下的内力及变形，如图5、图6所示。

通过对比图5、图6发现，速度的增加对立柱所承受的轴应力有着明显的影响，轴应力最大值及最小值均呈增长趋势且变化幅度较大，20km/h时轴应力最大值为31. 87kN/m2、最小值为-28. 8kN/m2;而50km/h时轴应力最大值已达到59. 40kN/m2，最小值增长为-61. 97kN/m2。故在长期超速荷载的作用下，立柱的轴向性能会受到一定的损坏。

y方向剪应力由于汽车荷载对称作用变化并不明显。而z方向剪应力则呈现出先上升后下降的趋势，由图5（e）～（f）曲线变化可预测在车速达到35 km/h左右时z方向剪应力可能会出现极值，此时立柱将承受较大的剪切力，可能会造成沿桥向剪切破坏。

4结论

（1）通过对比现场监测结果及数值模拟结果可以发现二者值大致接近，故本模拟结果可以使用。

（2）在未超过设计时速时，随着车速的增加，立柱轴力及z方向剪力有少量增加，y方向剪力几乎不变，x方向有较小变形。

（3）在超速时，车辆速度的增长对立柱轴应力有着显著的影响。立柱z方向剪应力在车辆超过设计时速后不久将达到峰值，故在长期车辆超速行驶下立柱有可能产生沿桥向剪切破坏。

（4）车速的变化对桥梁变形的影响并不是太大，故超速现象并不会直接影响到桥梁的变形损坏。

参考文献：

[1] ATAEI S，MIRIS. Investigating dynamic amplifificationfactor of railway masonry arch bridges through dynamicload tests[J].Construction and Building Materials，2018 ，183：693 -705.

[2] AKBARI M R，NIMAFAR M，CANJI D D，et，a1.Investi-gation on non-linear vibration in arched beam for bridgesconstruction via AGM method[J].Applied Mathematicsand Computation， 2017， 298： 95 -110.

[3]MOREIRA V N，FERNANDES J，MATOS J C，et，al.Reliability- based assessment of existing masonry archrailway bridges[J].Construction and Building Materi-als ，2016 ，115：544-554.

[4]CONEN H.DOCAN M，KARACASU M，et..Structuralfailures in refrofifit historical murat masonry arch rmdge[J]. Engineering Failure Analysis，2013， 35： 334-342.

[5]AYDIN A C，OZKAYA S G.The fifinite element analy-sis of collapse loads of single-spanned historic masonryarch bridges（ Ordu， Sarpdere Bridge）[J].EngineeringFailure Analysis， 2018， 84： 131 -138.

[6]CHARLES W J，DI S，YOZO F.Prediction of vehicle-induced local responses and application to a skewedgirder bridges[J].Engineering Structure， 2011 ，33：1088-1 097.

[7]ASHEBO D C，CHAN T H T，YU L Evaluation of dy-namic loads on a skew box girder continuous bridge partI： field test and modal analysis[J].Engineering struc-tures ，2007;29（6）：1 052-1 063.

[8] WANG T L，HUANG D， SHAHAWY M. Dynamic be-havior of slant-legged rigid-frame highway bridge[J].JStructure Engineering， 1994， 120（3）：885-902.

[9] KIM C W，KAWATANI M， KIM K B.Three-dimension-al dynamic analysis of vehicleinterection with roadway roughness[J].Computation structures， 2005， 83（ 19 -20）：1 627-1 645.

[10]邓露，何维，俞扬，等，公路车一桥耦合振动的理论研究和应用研究进展[J].中国公路学报，2018（ 31）：38 -54.

[11]《中国公路学报》编辑部，中国桥梁工程学术研究综述. 2014[J].中国公路学报，2014，27（5）：1-96.

[12]HUMAR J L，KASHIF A H.Dynamic response analy-sis of slab type bridges[J].Joumal of Structures Engi-neering， 1995， 121（1）：48-62.

[13]LEITO P N， SILVA J G S，VELLASCO P C G D， et，a1. Composite（ steel-concrete） highway bridge fatigueassessment[ J]. Joumal of Constructional Steel Re-search， 2011， 67（1）：14-24.

[14]汪莲，任伟新，赵青，等，桥梁工程[M].合肥：合肥工業大学出版社，2011：248-260.

[15]顾安邦，孙国柱，公路桥涵设计手册（拱桥下册）[S].北京：人民交通出版社，1996.

（责任编辑：丁寒）