桥面不平顺状态下含裂纹梁的车桥耦合振动分析
2020-02-07唐基凯
唐基凯
(长沙理工大学 土木工程学院, 湖南 长沙 410114)
目前对车桥耦合的研究已从只探究车桥本身(不考虑外部激励)相互耦合逐步深入到考虑外部激励(风荷载、撞击等)对车桥耦合的影响。桥面不平顺作为随机外部激励对车桥耦合振动有着重要影响。张建波等基于虚拟激励法对重力引起的确定性激励和桥面不平顺引起的随机激励对桥梁的动态响应进行了研究;盛国刚等利用三角级数模拟桥面不平顺,分析了桥面不平顺对车桥耦合振动系统动力效应的影响;Y. Zhang等采用非线性多弹簧轮胎动力分析模型,分析了分离和桥面不平顺对车桥交互系统的影响。此外,在桥梁使用寿命期间,由于荷载的动态交互作用,梁体极易产生裂纹,有必要分析含裂纹梁体的车桥耦合振动。C. Y. Fu模拟了裂纹切换瞬态(打开与关闭)对车桥耦合振动的影响;罗纪彬等分析了移动车辆荷载作用下含裂纹梁的非线性动力特性。上述研究忽略了桥面不平顺的影响,使研究结论不够完整。该文基于Hamilton原理,同时考虑桥面不平顺和梁体含裂纹,对车桥耦合系统动力响应进行研究,探讨裂纹深度、位置及桥面不平顺等级、行车速度、车辆质量等参数对车桥耦合系统动力响应的影响。
1 考虑桥面不平顺的车桥系统
如图1所示,设梁截面为矩形截面,梁长与梁高分别为l、h,在距左端支座l0处存在深度为a的表面裂纹。k1、c1分别为车辆悬挂系统的刚度与阻尼系数,M1、M2分别为车轮和车辆的质量,Z(t)为弹簧上车辆位移。设车辆以速度v匀速行驶通过桥梁,且车辆轮胎始终与桥梁点接触,不考虑脱离,则车轮与桥梁接触处的位移y(x,t)为:
y(x,t)=w(x,t)+r(x)
(1)
式中:w(x,t)为与桥面接触轮胎位移;r(x)为桥面不平顺值。
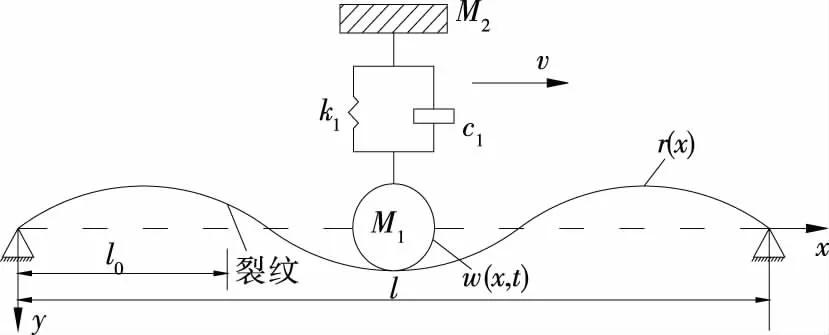
图1 车桥耦合振动模型
根据Hamilton变分原理,弹性变形体动力学变分一般表达式为:

(2)
式中:δT、δU、δW分别为系统的动能、应变能和外力功的变分。
设梁结构的密度为ρ,梁横截面积为A,梁竖向位移为w,则梁动能为:
(3)
系统的势能包括梁的形变势能Ub和裂纹位置释放的应变能Uk,令U=Ub-Uk,将梁简化为一维伯努利梁,只考虑其抗弯刚度,则梁的形变势能为:
(4)
式中:E、I分别为梁的弹性模量和惯性矩。
根据线性断裂力学理论,裂纹位置释放的应变能为:
(5)

裂纹处释放的应变能为:
(6)
外力功为:
(7)
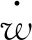
作用在梁上的外部荷载P(x,t)为:
P(x,t)=δ(x-vt){(M1+M2)g-
(8)
式中:δ为Dirac函数。
将式(3)、U=Ub-Uk、式(7)代入式(2),得到含裂纹梁的振动方程:
(9)

车辆动力平衡方程为:
(10)
式(9)和式(10)即为桥面不平顺时含裂纹简支梁与移动车辆系统动力耦合运动方程。
2 方程求解
简支梁桥的边界条件可写为:
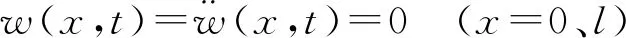

(11)
同理,由式(10)可得:
(12)
式(11)和式(12)即为考虑桥面不平顺时含裂纹梁车桥耦合系统动力控制方程。
3 桥面不平顺的模拟
桥面不平顺随机激励r(x)可按三角级数模拟:
式中:N为充分大的整数,为空间频率带的等分数;G2(ni)=4Gd(ni)Δn;n为空间频率;Gd(n)为位移功率谱密度,Gd(n)=Gd(n0)(n/n0)-w1;Gd(n0)为路面平整度系数;n0为参考空间频率值;w1为频率指数;ni=nd+(i-1/2)Δn(i=1,2,…,N);Δn=(nm-nd)/N;nm、nd为有效空间频率上、下限;x为桥面纵向坐标;φi为随机相位角,是满足均匀分布的介于[0,2π]间的随机数。
加速度功率谱Ga(n)、速度功率谱Gv(n)与位移功率谱之间的关系为:
Ga(n)=Gd(n)·(2πn)4
Gv(n)=Gd(n)·(2πn)2
桥梁不平顺考虑桥面等级为A、B、C、D 4个等级,其中A、D级桥面的模拟数据见图2。

图2 不同等级下桥面不平顺值
4 数值分析
采用Runge-kutta法对式(11)、式(12)联立的微分方程组进行求解。为验证上述方法的有效性,在忽略桥梁几何非线性和梁体裂纹的基础上得到车桥耦合系统桥梁的位移时程(见图3)。根据图3,采用上述方法得到的结果与文献[11]中结果吻合,上述方法可靠。
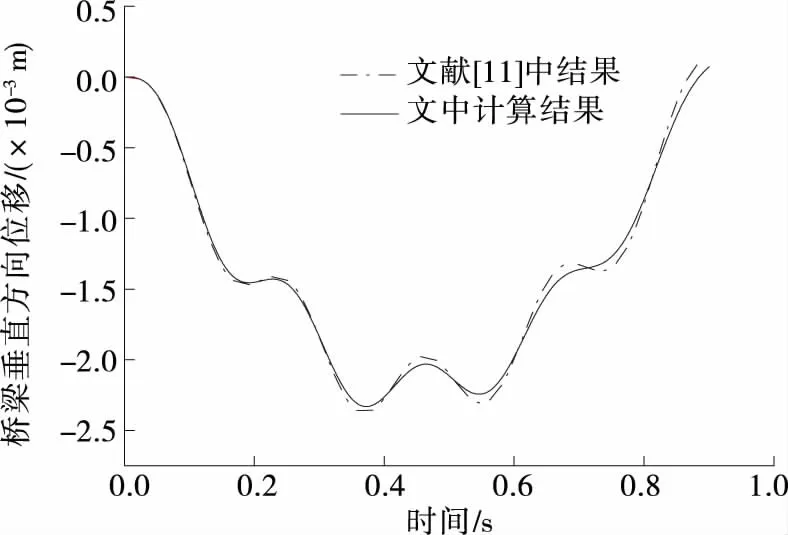
图3 忽略裂纹时梁体位移时程
桥面不平顺状态下含裂纹梁采取如下参数进行分析并忽略车轮质量:梁长l=40 m;弹性模量E=1.28×109N/m2;梁单位长度质量m=2 303 kg;惯性矩Iy=1.0 m4;梁体密度ρ=7 200 kg/m3;车体质量M2=2 000 kg;悬架刚度k=160 kN·s/m;车辆匀速经过桥梁的速度v=10 m/s;阻尼系数c1=2×103N·s/m;泊松比μ=0.2;梁体高度h=0.8 m;裂纹深度a=0.2 m;梁体横截面面积A=0.36 m2;l0=l/2。
图4为以A级桥面不平顺作为随机激励时梁体是否含裂纹及裂纹深度对车桥系统位移的影响。由图4可知:不管是否考虑裂纹,梁体波动的位移最大值都位于跨中附近;考虑梁体含裂纹时,梁体位移明显变大且位移增幅在跨中处更明显。裂纹深度从零增加到0.4 m时,梁体位移增加并不是线性的,裂纹深度从0.2 m增加到0.4 m时梁体位移增量比从零增加到0.2 m时的大。因此,在梁体位移幅值、不利位置处考虑梁体含裂纹是有必要的。

图4 梁体裂纹深度对车桥系统位移的影响
图5为裂纹深度为0.2 m时,忽略桥面不平顺及不同等级桥面不平顺对车桥系统位移的影响。由图5可知:系统跨中位移考虑桥面不平顺后围绕平顺状态上下波动,考虑桥面不平顺时跨中位移峰值比平顺下位移增大且受梁体波动更复杂。考虑不同等级桥面不平顺时,梁体波动曲线变化不大,但随着桥面不平顺等级的提高,梁体跨中位移峰值有所增大。说明桥面铺装的平整度对车桥系统的安全有一定影响。

图5 不同等级桥面不平顺对系统位移的影响
图6为裂纹深度为0.2 m、随机激励为A级桥面不平顺时,行车速度对车桥系统位移的影响。由图6可知:随着行车速度的增加,梁体位移增加,但梁体最大位移的位置不受速度影响,都集中在跨中附近;行车速度越大,梁体波动频率越小,行车速度低时出现多个位移峰值。这是由于梁体是弹性体,行车速度低时梁体部分挠度能自行恢复,而速度较高时,梁体变形不能及时恢复,导致其挠度增加。

图6 行车速度对车桥耦合系统的影响
设车桥质量比系数u=M2/(ml),考虑u为0.02、0.03、0.05。图7为车桥质量比对车桥系统动力响应的影响。由图7可知:随着车桥质量比的增加,梁体位移有所增加,但梁体波动频率并未改变。说明车辆质量增加会增加梁体波动位移,但不改变其振型。

图7 车桥质量比对车桥系统动力响应的影响
5 结论
(1) 桥面不平顺状态下考虑梁体含裂纹时,梁体跨中位移响应随裂纹深度增加而增加,且在跨中增加更明显,但裂纹深度线性增加时,梁体位移响应增加为非线性。
(2) 考虑桥面不平顺影响时,跨中位移响应比平顺状态下有所增大,不仅位移幅值增加,梁体的波动也更复杂。在不同等级桥面不平顺下,路面平整状态越差,梁体跨中位移幅值越大,考虑桥面平整状态对系统的安全有必要。
(3) 随着行车速度的增加,梁体位移增加,车速较高时梁体不能及时恢复变形而使第一次位移峰值变大且位置靠后。随着车桥质量比的增加,梁体位移有所增加,但车辆质量的增加并不改变其振型。
