基于组合近似模型的城市客车车架轻量化研究*
2020-02-07赵东伟尹怀仙张洪信赵清海付磊
赵东伟, 尹怀仙, 张洪信, 赵清海, 付磊
(青岛大学 机电工程学院, 山东 青岛 266071)
车架作为城市客车的核心零部件之一,是基本的承载、连接件,有着较大的质量占比。试验表明,汽车整备质量减少10%,能量消耗减少6%~8%,续航能力、转向灵活性等也得到提高。因此,在满足客车车架强度、刚度要求的前提下对车架进行轻量化十分必要。
由于传统的有限元优化分析方法计算量大、效率低,通常建立近似模型代替原始模型来处理复杂工程的结构优化问题。目前大多数研究是从多种近似模型中选择拟合精度最好的模型进行结构优化,对于复杂机械优化问题,各种近似模型对各种状态变量的预测能力表现各异,在优化设计中选取单一近似模型易造成局部最优。如Pan F.等利用单一的支持向量回归近似模型对目标函数进行优化迭代,其不能保证约束函数的全局精度;Chen S. K.等基于Kriging近似模型和水平集表征法对响应的不确定区域进行量化,其对试验设计采集的样本数依赖性较大,可能导致结果局部最优。因此,该文以某混合动力城市客车底盘车架为研究对象,通过对响应面、径向基神经网络、克里格及正交多项式4种近似模型的预测能力的对比分析,按照一定的权系数线性叠加建立组合近似模型,对城市客车车架进行结构轻量化优化设计,验证组合近似模型在城市客车车架轻量化设计中的可靠性。
1 建立近似模型
近似模型是通过建立相应数学模型来近似模拟一组激励参数与响应参数之间的关系,以精确拟合实际模型。其建立流程见图1。

图1 近似模型建立流程
1.1 径向基神经网络模型
径向基神经网络(RBF)以待测点与样本点之间的欧几里得距离为自变量,即假设x1,…,xN∈Ω⊂RN代表一组基函数的输入变量:
gi≡g(‖x-xi‖c)∈R(i=1,…,N)
(1)
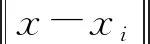
径向基函数的基本形式为:
(2)

1.2 响应面模型
响应面模型(RSM)基于数理统计技术,利用多项式函数拟合设计空间,具有计算效率高、适用范围广和鲁棒性好等优点。其基本形式为:
(3)
式中:xi为第i个设计分量;α0,αi,αij,αii,αijk,…,αii…i为多项式待定系数;d为响应面的最高阶数。
1.3 正交多项式模型
当试验因素较多时,采用最小二乘法求响应面模型参数的计算过程相当复杂,可采用正交多项式拟合响应面模型(Chebyshev)使计算过程简化,同时弥补使用最小二乘法求系数过程中的不足。
1.4 克里格模型
克里格方法(Kriging)是基于变异函数理论和结构分析,在规定区域内对区域化变量取值,并进行无偏、最优估计的一种空间局部内插方法。其基本表达式为:
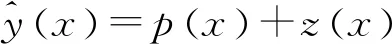
(4)
式中:p(x)为最基本的多项式;z(x)为均值为零的随机项,通常取高斯函数作为相关函数。
1.5 组合近似模型
组合近似模型(EM)由多个近似模型(如多项式、径向基函数、克里格和正交多项式等)加权线性叠加构成。其一般表达式为:
(5)
式中:yEN为组合近似模型的响应预测值;M为单一近似模型的个数;ωi、yi分别为第i个模型的权系数和响应预测值;设计变量x为矢量。
式(5)中权系数之和等于1。组合近似模型的关键是计算权重系数。采用启发式方法计算权重系数的公式如下:
(6)
(7)
(8)

2 单一近似模型精度分析
2.1 车架有限元模型
根据城市客车的二维图纸,利用CATIA软件构建车架几何模型并以IGES文件储存,导入有限元分析软件ANSYS中。网格单元尺寸为10 mm。划分网格后的车架网格单元为255 727个,节点为257 049个(见图2)。

图2 客车车架有限元模型
2.2 设计变量与响应的确定
车架轻量化设计中必须保证车架强度满足要求。以车架所受最大应力和总质量为响应量,选取车架中9个板料的厚度为设计变量(见图3),按照工程常用钢板厚度将X1~X9的取值范围设定为2~20 mm。
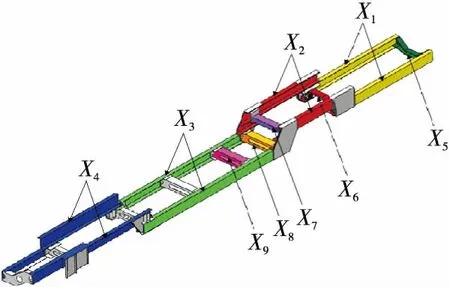
图3 设计变量的选取
2.3 最优拉丁超立方试验设计
对9个设计变量采用最优拉丁超立方试验设计产生样本点。最优拉丁超立方设计改进了随机拉丁超立方设计的均匀性,使所有试验点尽量均匀分布在设计空间,使因子和响应的拟合更精确真实。抽取200组试验样本组成试验设计矩阵(见表1)。
2.4 近似模型拟合效果分析
从响应拟合效果图可直观地看出近似模型的精度高低,响应拟合效果图中纵坐标为有限元分析得到的仿真计算值,横坐标为同一样本点通过近似模型预测的响应值,对角线代表真实的适应度,残差为零。采集的样本点落在对角线或其附近越多,则响应的预测精度越好。确定性系数R2和均方根误差RMSE反映近似模型的整体精度,其计算公式分别见式(9)、式(10)。要求R2≥0.9、RMSE≤0.2。

表1 试验设计数据 mm
(9)
(10)

以车架各主要承载梁X1~X9的厚度为优化输入变量、车架使用性能相关参数(总质量和最大应力)为优化输出变量,根据表1中样本点对4种近似模型的拟合效果进行分析。径向基神经网络近似模型的拟合效果和精度分别见图4、表2,响应面近似模型的拟合效果和精度分别见图5、表3,正交多项式近似模型的拟合效果和精度分别见图6、表4,克里格近似模型的拟合效果和精度分别见图7、表5。
由图4~7、表2~5可知:正交多项式近似模型中最大应力响应的确定性系数小于0.9,不能代替有限元模型进行计算;其他3种模型的精度符合要求,均可代替有限元模型进行后续优化设计。就响应的整体精度而言,克里格和响应面近似模型的整体精度最高;就车架最大应力响应的拟合精度而言,克里格近似模型的精度最好;就车架总质量响应的拟合精度而言,响应面和正交多项式近似模型的预测精度最高,克里格近似模型与之相比略有下降。综上,选取克里格和响应面模型构建车架最大应力和总质量的组合近似模型。

图4 径向基神经网络近似模型各响应的拟合效果

项目RMSER2最大应力总质量0.068 790.002 980.935 520.989 84
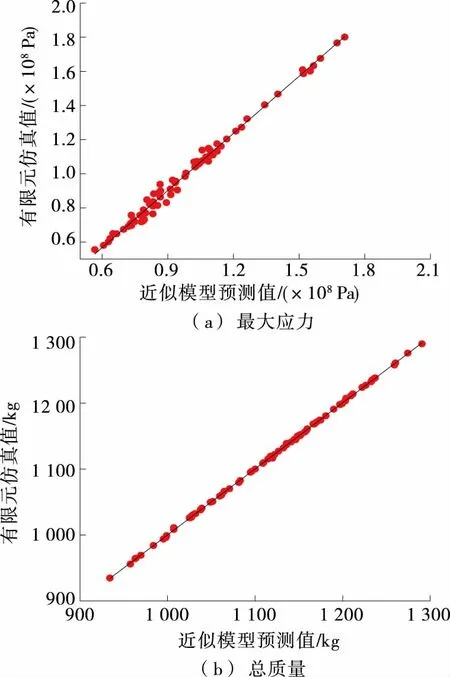
图5 响应面近似模型各响应的拟合效果

项目RMSER2最大应力总质量0.012 130.003 280.971 260.999 81

图6 正交多项式近似模型各响应的拟合效果

项目RMSER2最大应力总质量0.097 880.002 510.897 590.999 86
3 基于组合近似模型的车架轻量化设计
3.1 权系数的确定
采用启发式计算法,针对不同响应,根据式(6)~(8)计算组合近似模型中各单一近似模型的权系数,结果见表6。
利用单一近似模型的权系数构建组合近似模型,并对其拟合效果进行分析,结果见图8。
由图8可知:有限元仿真值和组合近似模型的预测值误差较小,预测精度略高于单一近似模型,且适合各种状态变量的预估。因此,可采用该组合近似模型代替有限元模型进行优化计算。
3.2 优化数学模型
以车架的最大应力和变形为约束、质量最小为目标的优化数学模型可定义为:

项目RMSER2最大应力总质量0.005 720.017 600.999 300.989 57

表6 近似模型的权系数

图8 组合近似模型各响应的拟合效果
(11)
式中:M(X)为车架的总质量;X为设计变量的可行域,X=[X1,X2,X3,X4,X5,X6,X7,X8,X9];Δrmax(X)为车架的刚度变形,其最大值为0.06 m;λ为强度安全系数,λ=1.5;σmax为车架受到的最大应力;σs为材料的屈服强度,σs=345 MPa。
3.3 模型求解
采用霍克-吉维斯直接搜索法在优化空间中寻找全局最优解。组合近似模型优化前后各设计变量的比较见表7。
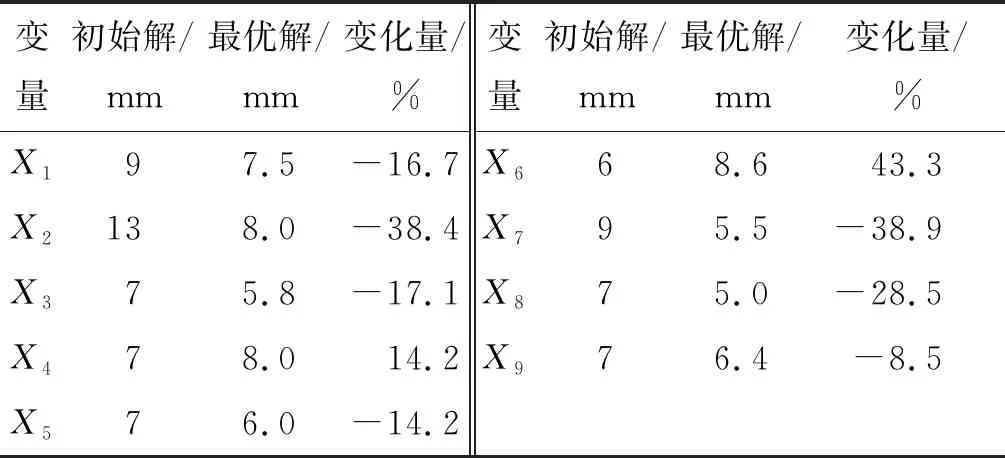
表7 优化前后各设计变量对比
对优化后车架重新建立有限元模型进行分析,结果显示:优化后车架质量为865 kg,比优化前的989 kg减轻12.54%;优化后车架的最大应力由187 MPa增至214 MPa(见图9),安全系数达到1.6,满足设计要求。

图9 优化前后车架等效应力(单位:Pa)
4 结论
(1) 比较响应面、径向基神经网络、克里格及正交多项式4种近似模型对车架状态变量的估算精度,克里格近似模型对最大应力的估算精度最高,响应面近似模型对总质量的估算精度最高。
(2) 基于克里格和响应面近似模型构建的车架状态变量估算组合近似模型对各类状态变量都有较高的估算精度,将其用于车架轻量化设计,与优化前车架相比,优化后车架减轻12.54%,优化目标得以实现;虽然应力有所增大,安全系数有所减小,但都在合理范围内。
