考虑车轮横向分布的钢桥面板顶板-U肋连接处疲劳损伤分析*

2020-02-07李行潘军唐雪松

公路与汽运 2020年1期

李行，潘军，唐雪松

(长沙理工大学土木工程学院，湖南长沙 410114)

正交异性钢桥面板由桥面板、U肋和横隔板焊接而成，是大跨度桥梁桥面系的首选结构形式。由于其特殊的结构体系、受力特性及焊接残余应力等缺陷，在车辆荷载长期反复作用下，顶板-U肋连接处易产生疲劳损伤。顶板-U肋在桥面板体系中是重要的受力部位，如果发生疲劳失效，不仅修复困难、费用高昂，而且严重影响结构的正常运行，显著降低结构的使用寿命和安全性能。尤其是萌生于焊根位置的顶板裂纹，前期裂纹未贯穿时难以发现，贯穿后则已大大降低了顶板-U肋连接处的正常工作性能。目前国内关于轮载的横向位置对顶板-U肋连接处的影响研究较少，有必要研究一种考虑轮载横向位置的有限元疲劳寿命评估方法。英国BS5400规范通过大量实验研究对构造细节进行疲劳等级评定，给出了各疲劳等级参数，理论成熟可靠，可为顶板-U肋连接处疲劳损伤计算提供依据。该文以广东佛山平胜大桥为研究背景，通过有限元分析找出全桥恒载作用下最不利节段，以该节段模型顶板-U肋连接处局部区域为研究对象，采用有限元方法，分析该区域在二轴和四轴货车加载下的应力分布，结合英国BS5400规范得到该细节的疲劳损伤；建立车辆轮迹分布模型，分析考虑轮迹横向分布概率后的疲劳损伤，为改善顶板-U肋连接处的抗疲劳性能提供理论依据。

1 有限元模型

1.1 全桥有限元模型

佛山平胜大桥是世界上跨度最大的单跨单塔双幅四索面自锚式悬索桥，主跨跨径为350 m，主梁采用钢加劲梁，闭口U肋的正交异性钢桥面板构造。

采用通用有限元软件ANSYS建立全桥有限元模型，模型共810个节点、937个单元。主梁、主塔和横梁采用具有承受拉、压、扭和弯曲性能的单轴梁单元Beam44模拟；吊杆和拉索选择仅轴向受拉或受压的杆单元Link10模拟；主梁和吊杆通过钢臂连接，采用Beam44单元模拟(见图1)。

图1 全桥有限元模型

根据李爱群等的研究结果，行车荷载对节段应力的影响不大，可不予考虑。通过ANSYS对该桥进行受力分析，得到恒载作用下全桥的内力分布(见图2)。根据材料力学公式σ=My/Iz(M为横截面上的弯矩；y为所求应力点的纵坐标；Iz为横截面对中性轴的惯性矩)，对于等截面的钢箱梁，Iz和y相同，弯矩M最大处即为截面最大应力处。根据ANSYS计算结果，该桥129号单元的弯矩最大，据此确定由128、129、130、131号单元组成的共12 m长节段为危险节段。

图2 恒载作用下弯矩云图(单位：kN·m)

1.2 节段模型

建立该桥危险节段有限元模型，分析车轮不同横向位置下钢桥面板顶板-U肋处的应力幅。取纵桥向4个横隔板12 m长节段，顶板厚度为16 mm，底板厚度为14 mm，纵隔板厚度为12 mm，横隔板厚度为10 mm，U肋的长度×高度×厚度为300 mm×280 mm×10 mm，顶板与U肋的夹角为78°，横隔板间距为3 m，U肋间距为300 mm。模型均采用Shell63壳单元，面板网格尺寸为300 mm×250 mm，弹性模量为210 GPa，泊松比为0.3。对胎压作用的5个U肋局部进行网格加密(见图3)。

图3 危险节段模型

为模拟节段模型在全桥中的受力特点，按节段模型在全桥中的实际受力进行加载：先约束一个端面所有节点的自由度，在另一端面附加一块钢板，将节段在该截面承受的弯矩、剪力与轴力作用在钢板形心位置，求得端面节点反力；撤掉钢板，约束该端面所有节点的自由度，将求得的节点反力作用于另一端面，将求得的节点反力作为力的边界条件加载至节点。e为轮载中心线距待测U肋中心线的距离，以轮载中心线每移动100 mm作为一个加载工况，在5个U肋横桥向宽度范围内加载，共30种工况，分析车轮不同横向位置对顶板-U肋连接处疲劳损伤的影响。实测发现U肋腹板与底板相交的角点处应力较大，有必要分析该处的疲劳损伤。因此，布置C1、C2、C33个测点，分析U肋的疲劳损伤分布情况(见图4)。

图4 荷载工况

2 轮载不同横向位置对疲劳应力的影响

2.1 疲劳荷载模型

根据王益逊的研究成果，二轴货车占货车总数的35%，四轴货车占货车总数的41%，对顶板-U肋处的疲劳影响较大。按照疲劳损伤等效原理求出货车的车辆荷载模型(见表1)。单轮着地面积为200 mm×300 mm，双轮着地面积为200 mm×600 mm。考虑铺装层厚度对车轮着地面积的影响，铺装层厚度为50 mm，车轮呈45°扩展至钢桥面板，修正后的单轮着地面积为300 mm×400 mm，双轮着地面积为300 mm×700 mm。

表1 疲劳车等效轴重

2.2 应力分析

在二轴车和四轴车不同横向位置下，测点C1的等效应力分布见图5。由图5可知：随着轴重的增加，顶板-U肋连接处的应力增大；车轮逐渐靠近被测U肋时，顶板-U肋连接处的应力逐渐增大；车轮作用于被测U肋的正上方时，应力达到最大值；随后随着车轮的逐步偏离，应力逐渐降低；在前轮作用下，e为1 000～2 000 mm时，测点应力变化明显，该范围之外应力无明显变化。由此可知单轮对顶板-U肋连接处的应力横向影响范围为1 m，双轮对顶板-U肋连接处的应力横向影响范围为1.5 m。由于日常车流中车辆间距通常大于1.5 m,中国规范给出的车辆荷载同轴轮距为1.8 m，在横桥向可忽略多车效应及轴重间的相互作用对顶板-U肋连接处的影响。

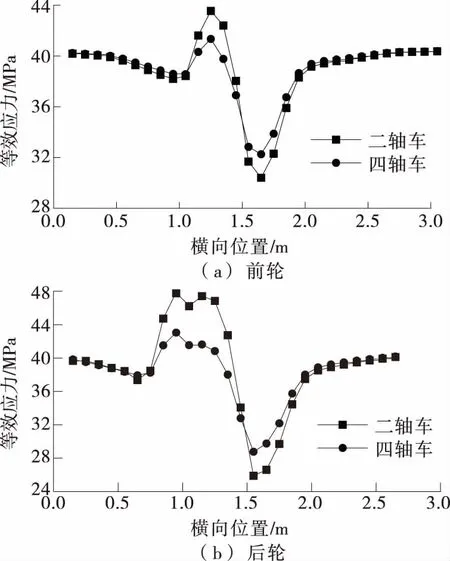
图5 不同横向位置下C1测点的等效应力分布

图6为二轴车作用在不同横向位置时各测点的等效应力分布。由图6可知：不管是前轮还是后轮，C1、C2、C3测点的应力变化规律不同。车轮作用在目标U肋左侧相邻U肋上时，C1测点承受较小的拉应力。随着车轮的移动，该处逐渐由拉应力变为压应力，当车轮移动到目标处时，应力变化显著。主要是由于顶板与U肋腹板的相互约束，使车轮作用下局部受压。C2与C3测点的变化规律相同，但在相同荷载作用下，C3点的应力比C2点的大很多。

3 顶板-U肋连接处局部疲劳损伤分析

根据Miner线性累积损伤理论，结合英国桥梁规范BS5400，计算各类疲劳车各测点的日损伤度，了解顶板-U肋连接处在不同横向位置下的疲劳损伤情况。疲劳累积损伤采用Miner公式估算：

式中：ni为第i个应力幅的循环数；Ni为对应于第i个应力幅的疲劳寿命。

根据BS5400中σr-N(S-N)关系规定进行计算：

图6 不同横向位置下各测点的等效应力分布

式中：N为在应力幅σr作用下构件发生破坏所需次数；K2、m根据构件的疲劳等级查规范得到。

对于低于疲劳极限σ0的σr，根据规范中低值应力循环的处理办法，按下式处理：

采用上述方法进行计算，得到二轴车、四轴车作用在最不利位置时各测点的疲劳损伤度(见表2)。由表2可知：轴重对顶板-U肋连接处日损伤影响较大，二轴车前轮相较于四轴车前轮重20%，而造成的日损伤约为四轴车的2倍，重车所引起的疲劳损伤危害更大，应加强对超载车的管理；U肋损伤分布差异巨大，如在四轴车后轮作用下，C3测点的损伤度约为C2测点的1 000倍，说明U类腹板处疲劳损伤较小，而腹板与底板相交处和U肋底板损伤较大；C1测点的疲劳损伤比C3测点的小，是由于未考虑焊缝的影响，应在该处加一初始损伤，考虑焊缝和由结构自身缺陷带来的影响。

表2 二轴、四轴车最不利位置下各测点的日损伤度

4 考虑车轮横向分布的疲劳损伤评估方法

4.1 车轮横向分布概率模型

根据已有研究成果，车辆的横向分布受到诸多因素的影响，但仍具有一定的分布规律。为求得车轮横向分布对该桥顶板-U肋连接处的影响，作如下假设：各车道间车流相互独立，不受干扰；各车道车轮的横向分布服从正太分布。车轮分布模型为：

将车轮分布模型沿车道进行积分，得：

计算得σ=539 MPa，则车轮分布模型为：

实际上，车辆轮迹有一定宽度，车辆通过时只能覆盖一小部分车道宽度。因此，在车道上车轮的横向位置分布并不均匀。将该模型进行分段积分，求得车轮经过不同横向位置的概率(见图7)。

图7 车轮横向概率分布

4.2 考虑车轮横向分布的疲劳损伤评估

先计算车道的日交通量，根据车型占有率得到各轴车的日通行数，考虑车轮横向分布概率得到各轴车在不同横向位置的作用次数：

nij=VdPiPj

式中：nij为第i种车在第j个横向位置的作用次数；Vd为日交通量；Pi为第i种车型的占有率；Pj为车轮横向分布概率。

根据上述方法进行计算，得到考虑轮载横向分布的各测点日疲劳损伤度(见表3)。由表3可知：在二轴车后轮作用下，考虑车轮横向分布时C1测点的日损伤度为2.995 73×10-7，相较于最不利位置下的日损伤度，C1测点的损伤度下降约85%；在四轴车后轮作用下，考虑车轮横向分布时C2测点的日损伤度为4.493 02×10-8，相较于最不利位置下的日损伤度，C2测点的损伤度下降约63%。综合各测点在前后轮作用下的损伤度，损伤度平均下降约69%，疲劳寿命得到大幅提升。可见，车轮横向分布对顶板-U肋连接处疲劳损伤的影响显著，研究该处疲劳损伤时应重视车轮横向分布概率的影响。