转体施工中转动体系有限元分析

杨柳， 张清， 王阳建， 陈得良

(1.长沙理工大学 土木工程学院， 湖南 长沙 410114；2.深圳市路桥建设集团有限公司， 广东 深圳 518024)

转体施工是在非设计轴线处将主体施工完毕，再旋转至设计位置的一种施工方法，分为平转法、竖转法及平竖结合法。对于平转法，转动体系是核心部分，通常由下转盘(承台)、球铰、上转盘(承台)及转动牵引系统组成。目前国内关于小半径弯桥平转的转动系统研究较少。该文以广深沿江高速公路深圳段二期工程深中通道深圳侧接线H匝道大曲率钢箱梁转体施工为例，对设置横向预偏心的转体结构进行分析探讨。

1 工程概况

深中通道深圳侧接线H匝道桥位于广深沿江高速公路深圳段二期工程SJ1合同段，其中第五联横跨既有一期匝道和广深(广州—深圳)高速公路，采用转体施工法。为跨径(50+80+50) m的连续曲线钢箱梁，曲线半径150 m。转动体系见图1。

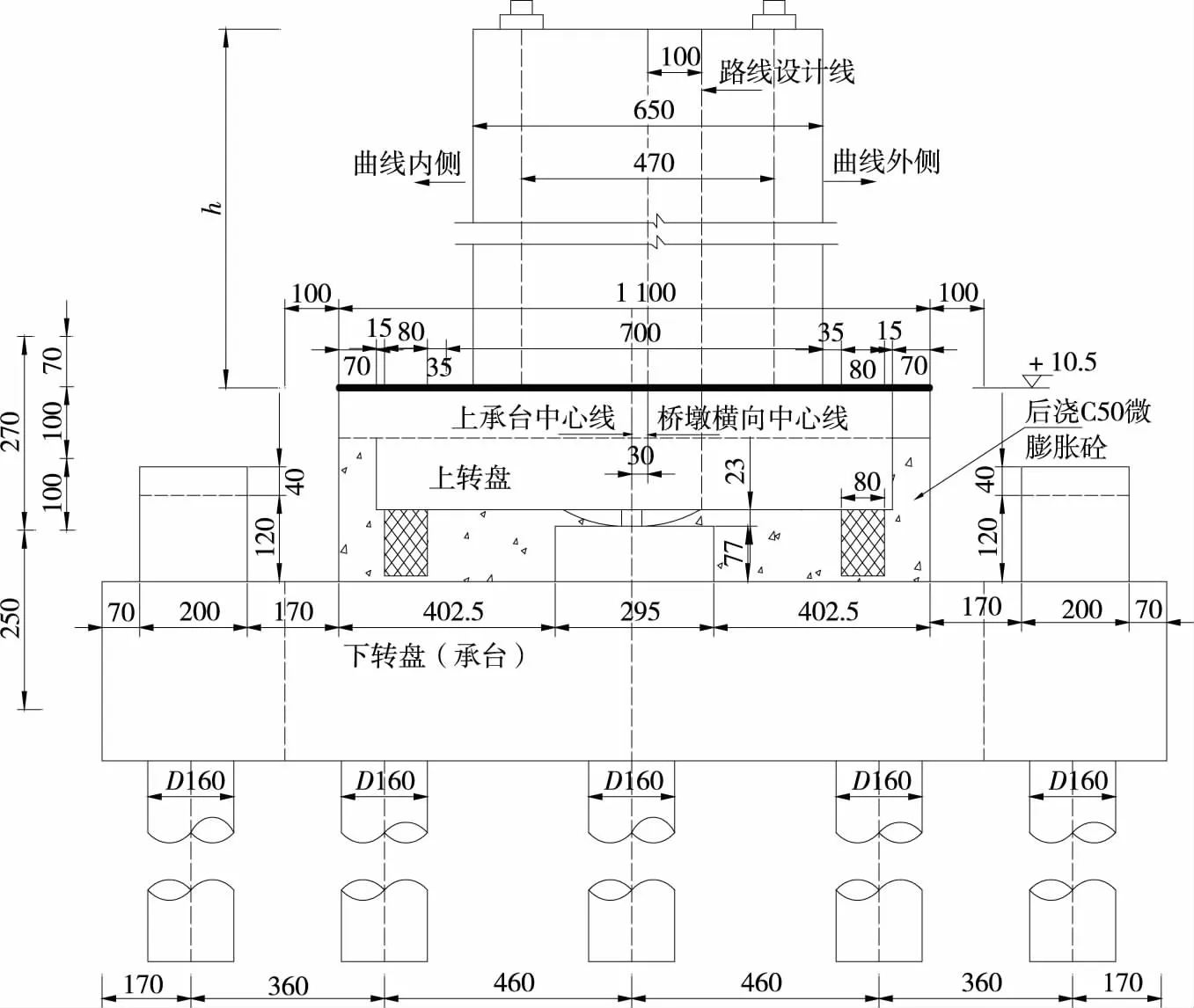
图1 深中通道深圳侧接线H匝道桥转动体系立面图(单位：标高为m,其他为cm)

因转动主体曲线桥存在很大横向偏心，桥墩横向中心线设计偏离箱梁轴线(图1中路线设计线)1 m，而转动体系的中心线(图1中上承台中心线)偏离桥墩中心线0.3 m，共设置1.3 m横向预偏心。

转动体系砼结构采用C50砼，钢球铰作为转动体系的关键部位，采用Q345钢材，直径225 cm，厚4 cm，分上下两片。下转盘上设转动系统的下球铰、保险撑脚环形滑道及转体拽拉千斤顶反力座等。下球铰砼灌注完成后，将直径24 cm钢棒放入下转盘预埋套筒中，方便中心轴转动，然后进行下球铰聚四氟乙烯滑动片和上球铰安装。上转盘直径960 cm，高100 cm，桥墩与上转盘之间设(1 100×1 100×70) cm上承台。上转盘布设纵横向预应力钢筋，内预埋转体牵引索，其是转体牵引力直接施加的部位，下设8组撑脚，对称分布于纵轴线的两侧。撑脚的下方(即下转盘顶面)布置90 cm宽滑道，滑道半径425 cm，其中撑脚走板与滑道的间隙为6 mm。

2 有限元模型

利用ANSYS有限元软件模拟桥墩、上承台、上转盘、撑脚、钢制球铰及转动中心轴，上、下钢球铰及转动中心轴采用Solid185单元模拟，砼结构采用Solid65单元模拟，各接触面之间采用接触单元模拟，上球铰底部的凸面和转轴表面用Conta174单元生成接触单元，上球铰空心处与转轴接触的凹面及下球铰顶部的凹面采用Targe170单元生成目标单元，摩擦系数为0.047。有限元模型见图2。

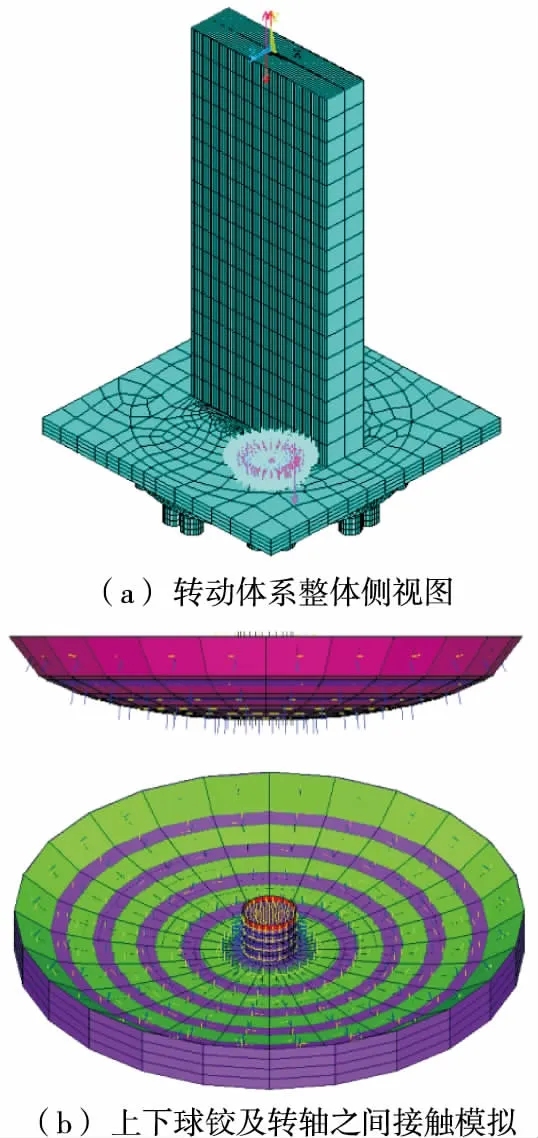
图2 ANSYS有限元模型

对下球铰进行固定约束，x轴表示横桥向，正向为钢箱梁的曲线外侧，z轴表示纵桥向，yoz面与转动体系的中心面重合。为模拟真实荷载，各结构均采用实际尺寸。此外，由于曲线桥存在横向偏心，前期计算出钢箱梁的质量重心向曲线内侧偏离箱梁中心线1.573 2 m，设计预偏心1.3 m，故在曲线内侧横向偏离转盘中心线0.273 2 m的节点处加载集中荷载来模拟桥梁主体的自重，钢箱梁主体重738.7 t。

3 静力分析

3.1 挠度变形分析

撑脚布置见图3，坐标轴的方向与图2有限元模型的坐标轴方向一致，x轴正向为曲线外侧，下文中曲线外侧均指x轴正向。

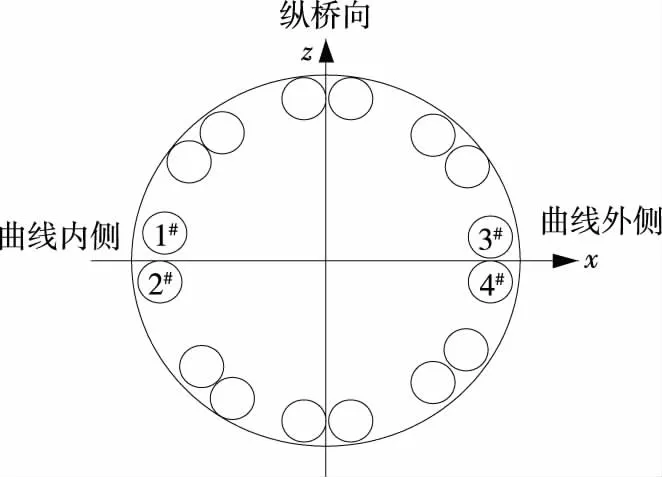
图3 8组撑脚的分布

转体系统在钢箱梁主体及桥墩自重的横向偏载作用下的变形见图4。由图4可知：在自重作用下转体体系的变形非常小，不超过1 mm，且曲线内侧结构变形大于外侧结构变形；曲线内侧的撑脚(图3中的1#、2#)变形最大，曲线外侧的撑脚(3#、4#)变形最小；转体体系中变形位移有正有负(曲线外侧出现下挠)，表明对于偏心转体施工，设置预偏心后，当整体结构中心与转动中心不能完全一致时，很小的偏心距都会造成转体结构变形，产生局部微小上翘和下挠。因此，对偏心转体施工应严格控制整体偏心距，使整体重心基本与转动中心吻合。

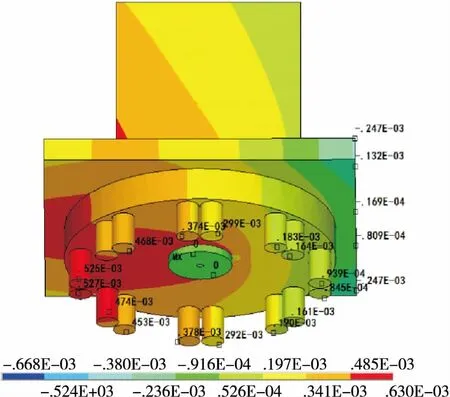
图4 转动体系静力分析变形(单位：m)

3.2 砼结构应力分析

图5为转动体系砼结构的应力云图。

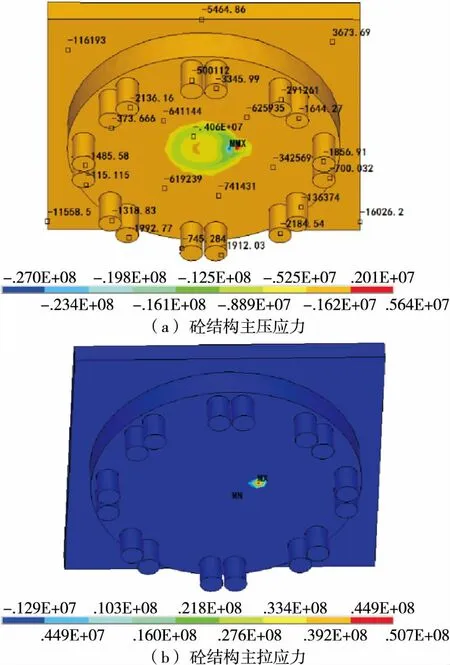
图5 转动体系砼结构应力云图(单位：Pa)

由图5(a)可知：转动体系砼结构整体处于受压状态，上转盘底部与上球铰接触的区域主压应力较大，最大值为-27 MPa，由于上转盘为C50砼结构，上球铰采用Q345钢材，应力状态满足要求；大部分主压应力不超过1.62 MPa，主压应力较小。

由图5(b)可知：在上转盘底部与上球铰接触边的曲线外侧出现主拉应力集中现象，最大主拉应力为50.7 MPa。因为上球铰是Q345钢制结构，可认为上转盘与上球铰接触区域的应力满足要求，但设计时应增加该部位受拉钢筋配置。

3.3 球铰应力分析

图6为球铰应力云图。由图6(a)、(b)可知：上球铰整体处于受压状态，主压应力为0～-144 MPa，钢球铰采用Q345钢材，最大主压应力符合要求；位于横向轴线曲线外侧位置，越靠近球心压应力越小。在上球铰空心处的曲线外侧及顶部边缘曲线外侧靠近横向轴线处出现主拉应力集中现象，主拉应力为0～44.7 MPa，最大主拉应力出现在上球铰边缘曲线外侧且靠近横向轴线上部。

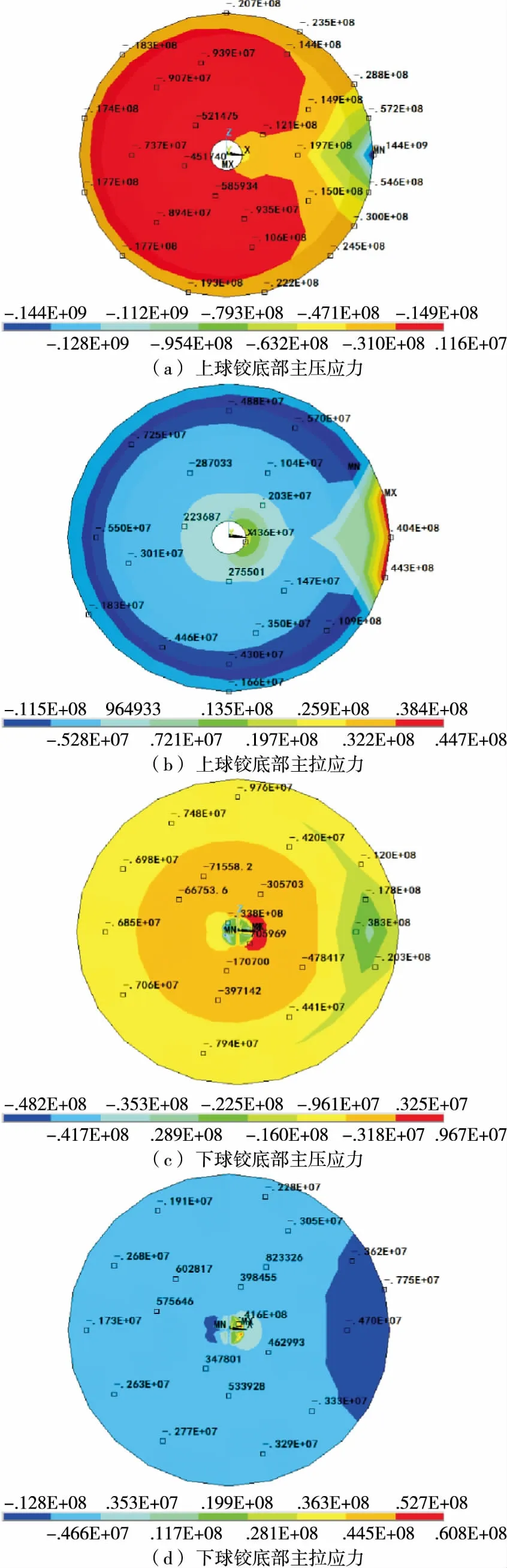
图6 球铰应力云图(单位：Pa)

由图6(c)、(d)可知：下球铰整体处于受压状态，下球铰的曲线外侧和转动中心轴的底部主压应力较大，为0～-48.2 MPa，最大主压应力出现在转轴底部的曲线内侧；靠近转轴处的下球铰底部出现较大主拉应力，为0～60.8 MPa，最大主拉应力位于下球铰底部与转轴相接位置的曲线外侧。

4 牵引力的计算与加载

根据JTG/T F50-2011《公路桥涵施工技术规范》，中心支撑转体施工所需牵引力为：

124.89 kN

式中：f为静摩擦系数，为保证足够的牵引力，f取0.1；G为转体总重量；R为上球铰半径；D为上转盘直径。

转体施工中牵引力施加在上转盘，则有限元模型对上转盘施加圆周力可进行转动分析，所施加圆周力的大小即为牵引力124.89 kN，均分到上转盘外圆周面的各节点。

加载牵引力后，挠度变形仍不超过1 mm且各部分应力变化不大，表明加载刚刚克服静摩擦力的牵引力，整个结构处于接近平衡状态，转动过程也较平稳。

5 桥梁主体对转动体系的影响

5.1 桥梁主体偏心的影响

提取图3中1#～4#撑脚中心处的节点，得到撑脚的变形[见图8(a)]和转动体系的应力随桥梁主体偏心的变化[见图8(b)]。

由图8(a)可知：随着曲线桥逐渐向轴线内侧横向偏心，位于箱梁重力偏载一侧即曲线内侧的撑脚(1#、2#)不断下挠，曲线外侧撑脚(3#、4#)则逐渐上挠，表明随着桥梁主体向曲线内侧不断偏心，整体重心会向曲线内侧逐渐偏离；当弯桥的横向偏心小于1.9 m时，曲线内侧撑脚的变形量大于曲线外侧，即位于重心一侧的撑脚的下挠值大于非重心一侧的上挠值。

图7 转动体系受力简图(单位：m)

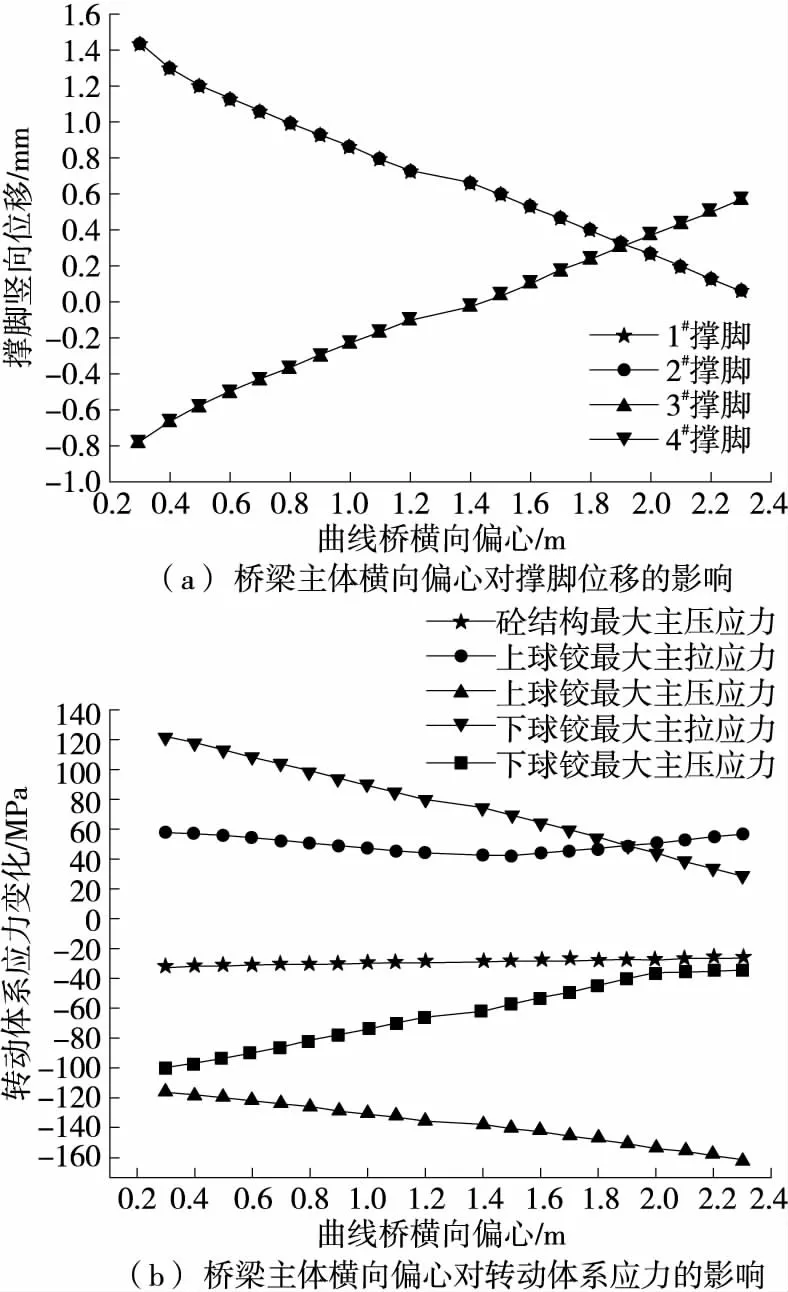
图8 桥梁主体偏心的影响分析

由图8(b)可知：转体系统砼结构的应力与桥梁主体的偏心没有很大关系，下球铰的最大主拉应力和最大主压应力均随偏心的增大而线性减小。对于上球铰，最大主压应力随桥梁主体横向偏心的增大而线性增长，最大主拉应力呈上抛物线，但变化不大。整体来说，下球铰主拉、主压应力减小速率小于上球铰主压应力增大速率。

5.2 转动主体吨位的影响

曲线桥主体质量对转动体系有很大影响。桥梁主体重量为0～2万t时，撑脚位移变化见图9(a)，转体系统各部分应力变化见图9(b)。

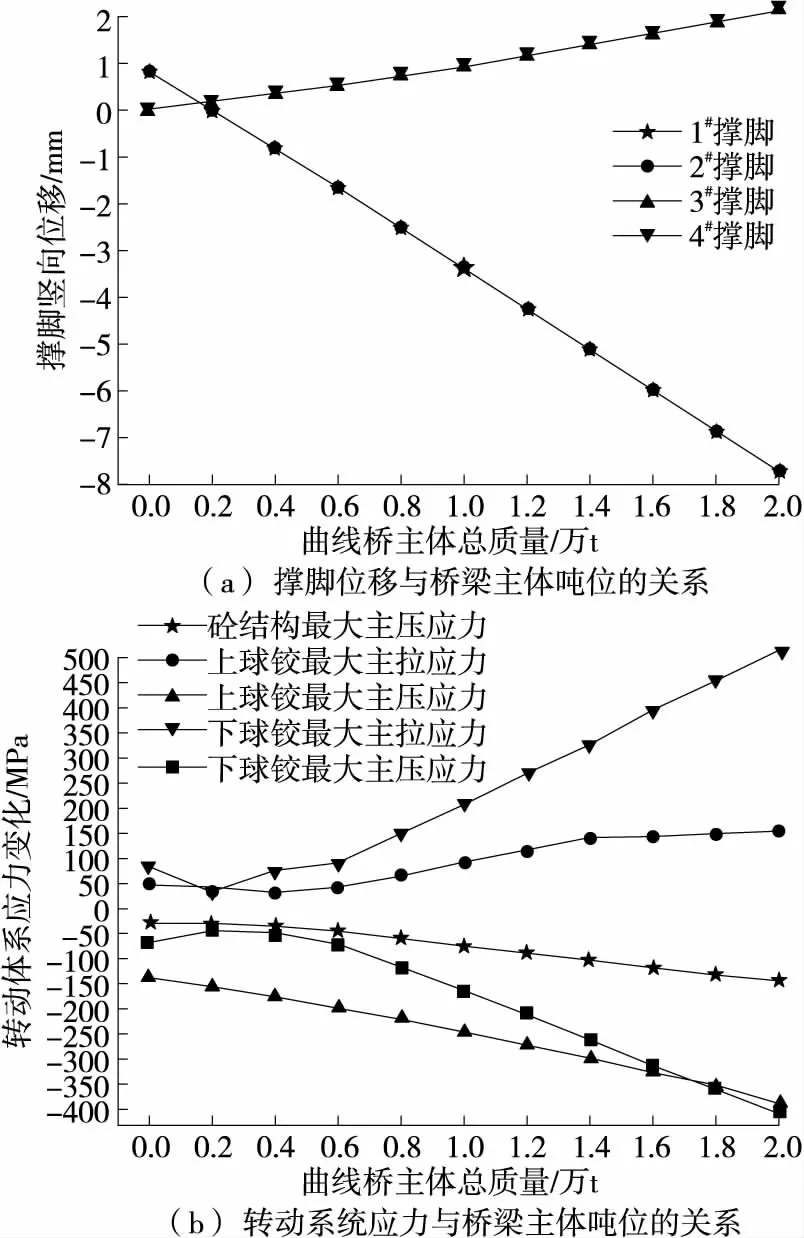
图9 桥梁主体吨位的影响分析

由图9(a)可知：随着曲线桥主体质量的增加，曲线内侧撑脚(1#、2#)下挠越来越明显，曲线外侧撑脚(3#、4#)则不断上挠，整个转体系统变得越来越倾斜。转动主体的总质量达到1.6万t时，在恒载作用下撑脚变形大于6 mm，撑脚已与滑道接触，进入抵抗倾覆状态。

由图9(b)可知：曲线梁质量越大，转体结构各部分的主压和主拉应力不断增大；转动主体质量超过0.8万t时，下球铰的主压和主拉应力增长速度最快。对于该转体系统，当主梁总质量超过0.5万t时，砼结构会遭到破坏，而钢球铰可承受转动主体的质量最大为1.6万t。

6 结论

通过对设置横向预偏心的转体系统进行仿真模拟与数值分析，得以下结论：

(1) 转体施工曲线桥梁设置预偏心后，整个结构接近平衡状态，变形和应力均满足要求，其偏心距稍微偏离曲线外侧，无需配重。转体施工前判断合理的预偏心非常重要。

(2) 转动系统整体受压，结构安全。但在上转盘与上球铰、上球铰与下球铰、转动中心轴接触的位置及上球铰底部曲线外侧边缘会出现主拉应力，应重点监控。此外，在上转盘与上球铰的接触区域需增加受拉钢筋数量。

(3) 设计转体系统时应考虑弯桥的横向偏心及总质量。横向偏心对砼结构的应力作用不大，但随着横向偏心的增大，上球铰的主压应力增大，而下球铰主拉、主压应力减小。转动主体质量对下球铰主拉、主压应力的影响最大。对于横向大偏心的转体施工桥，应注意上球铰的抗压能力；大吨位的转体施工桥，应注意下球铰的抗拉、抗压能力。此外，在设计和施工中应注意位于桥梁重心一侧撑脚的变形，因为即使设置预偏心和配重后整体结构的偏心距非常小，对于大吨位转体施工桥，桥梁重心一侧的撑脚变形也会大于撑脚走板与滑道的间隙。