模态缺陷条件下的深潜耐压球壳极限强度

熊志鑫， 黄志权， 张道兵， 胡雄

(1.上海海事大学 海洋科学与工程学院，上海 201306； 2.上海海事大学 物流工程学院，上海 201306)

潜器在水下工作时承受很大的深水压力，其耐压壳多采用球形结构[1]。在研制大深度潜器的设计中，耐压球壳结构的强度与稳定性分析是设计的关键技术之一，受到越来越多研究人员的关注[2-3]。随着研究的不断深入和安全性能要求的不断提升，结构的强度问题由完善耐压球壳研究深入到观察窗[4]、含开孔[5]、考虑焊接效应[6]、带初始挠度[7]等缺陷的壳体研究。针对含有初始缺陷球壳的非线性失稳方面的研究，主要是基于局部缺陷[8]和模态缺陷[9]展开。出于耐压壳安全性考虑，模态缺陷往往被作为最差缺陷引入。欧洲标准明确指出，几何缺陷的形状应取最差缺陷，即导致壳体屈曲载荷下降最快的缺陷[10]。在最差缺陷形状未知的情况下，建议采用模态缺陷来分析壳体的屈曲特性。第一阶线性屈曲失稳模式往往被作为最差缺陷引入[11]，这在钢结构行业中也称为一致缺陷模态法[12]。但是，对具有相近分立特征值壳体，存在多模态屈曲现象，第一阶线性屈曲失稳模式往往不是最差缺陷，高阶线性屈曲失稳模式也可能导致较低的屈曲载荷[13]。文献[14]研究了多种缺陷形式对轴压柱形壳体屈曲特性的影响规律，发现第一阶线性屈曲失稳模式并非柱形壳体的最差模态缺陷。

为此，本文研究了基于前15阶模态缺陷耐压球壳的极限强度，比较了各阶模态缺陷对应极限强度的差值，并在210种不同随机缺陷样本的统计基础上，研究各阶模态缺陷计算对应的可靠性。在可靠性较高的模态缺陷条件下，分析不同半径厚度比对缺陷幅度的敏感度。

1 模态缺陷方法

工程分析结构缺陷的常用方法是用一阶屈曲模态模拟结构的初始几何缺陷，这种方法在确定结构的缺陷敏感性时是十分有效的，但不一定是最差缺陷状态。模态缺陷方法则是将特征值屈曲分析计算得出的前N(N是正整数)阶模态作为结构的N个初始缺陷的分布模式。分别计算这N个模态缺陷形态对应的临界屈曲荷载，比较它们的大小，并进行可靠度分析。本文以耐压球壳的前15阶屈曲模态作为研究对象展开分析。

1.1 计算模型

文献[15]分析了一种钛合金深潜耐压球壳的极限强度，并得到了极限强度计算的经验公式。其所采用球壳模型的参数为：内径D=2 100 mm，壳厚t=10 mm，材料弹性模量E=1.148×105MPa，泊松比υ=0.3。

建立上述球壳的有限元模型，模型单元为减缩四边形单元S4R，单元网格大小为50 mm，共得到23 330个单元节点和7 776个四边形单元。边界条件使用简支的三点约束6自由度的方法，在x轴上的2个节点分别添加条件约束y轴和z轴方向的位移即T2=T3=0，在y轴上的1个节点添加条件约束x轴和z轴方向的位移即T1=T3=0[9]。

文献[16]计算得出该耐压球壳结构在完善状态下的极限强度为12.51 MPa。

1.2 计算结果

采用模态缺陷法，将上述耐压球壳的前15阶弹性屈曲模态作为结构的初始几何缺陷分布形态，对其进行极限强度计算：1)进行耐压壳结构特征值屈曲分析，提取结构前15阶屈曲模态。2)参考相关规范和实际制造误差，确定最大缺陷幅值[17]，并引入计算模型。3)采用弧长法对结构进行非线性屈曲分析。施加不同初始缺陷后，结构的非线性屈曲计算结果如表1所示。

表1 屈曲模态阶数与对应的极限强度(最大缺陷幅值为1.758 3 mm)Table 1 Buckling mode and ultimate strength (the maximum defect amplitude is 1.758 3 mm)

从表1可以看出，考虑1～15阶屈曲模态缺陷后，耐压球壳的极限强度在第5阶模态缺陷条件下达到最大值为7.23 MPa，在第15阶时最小值为6.20 MPa，分别为完善球壳的59.5%和51.0%。由上述计算结果可以看出：结构对初始几何缺陷较为敏感，极限强度较完善球壳大幅降低；按一致缺陷模态法施加的第1阶屈曲模态并非结构的最不利初始缺陷。因此，需要考虑前几阶甚至前几十阶的模态缺陷条件进行比较，才能较准确评估耐压壳结构的安全性。

2 不同模态缺陷的可靠度计算

为了评估上述若干阶模态缺陷条件耐压壳结构的可靠性，引入随机缺陷模态法[18]，求出极限荷载对应的概率分布。

在工程设计中，随机缺陷方法能够较为真实地反映结构的工作性能，所求的的极限荷载结果更能客观地反映结构的情况。假设耐压球壳在生产制造中导致的缺陷遵循正态分布[19]，即是球壳有限元模型的各个网格节点在x、y、z3个方向的坐标值符合各节点理论坐标值的均值为μ，待求值σ为方差的正态分布。假定各节点的位移误差为±δ，实际坐标值为X1，理论坐标值为X0，则符合正态分布的各节点坐标值满足如下分布：

(1)

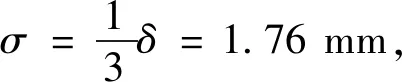
通过坐标位置偏差作为随机缺陷引入原始模型，相继建立210组球壳随机模型用于非线性屈曲计算分析。对210个样本进行非线性屈曲计算，结果的统计直方图如图1所示。其中，极限荷载最大值为7.83 MPa，最小值为5.58 MPa，均值7.22 MPa。

图1 极限荷载值统计分布Fig.1 The statistical distribution of ultimate loads

由图1可知，极限荷载值的统计直方图符合正态分布特征。随机缺陷模态法计算耐压球壳的临界屈曲荷载服从均值μ=7.22,方差σ=0.324 的正态分布规律。根据正态分布函数可以对每一阶模态对应的临界屈曲荷载进行可靠度计算，计算结果如表2所示。

表2 1～15阶模态缺陷极限强度值的可靠度Table 2 Reliability of ultimate strength from the 1～15th order modal imperfections

由表2可以看出，第1阶、10阶、14阶和15阶模态缺陷具有99%以上的可靠度，其中第15阶模态缺陷的可靠度最高，达到99.94%。

3 缺陷敏感性分析

当考虑结构的初始缺陷后，其非线性屈曲的分析变得更为复杂。结构对初始缺陷的敏感性分析将有助于进一步了解结构的屈曲性能。本文第1节是基于标准规范允许的最大缺陷作为幅值分析了最大几何缺陷对极限强度的影响程度。但是，工程制造中可能存在更多其他缺陷值情况。因此，需要计算不同的缺陷幅值对耐压壳的影响，进一步明确耐压壳失稳的机理，为耐压壳的设计提供参考。

3.1 缺陷幅值对临界屈曲荷载的影响

为分析缺陷幅值对临界屈曲压力的影响，在确定厚度t和半径Rm后，对每类球壳设置不同的缺陷幅值，再计算得到每个缺陷幅值对应的临界屈曲压力。计算结果的曲线如图2所示。图2中分析计算选取的厚度t为10、15、20、 25、 35、45、55、65、75、85, 95、105 mm，共12组。缺陷幅值为0.1、0.3、0.5、0.7、1、2、4、6、8、10 mm，共10组。

从图2所示的曲线可以看出，随着缺陷幅值的不断增加，结构的临界屈曲压力值近似均匀下降，没有出现跳跃的现象，且不同厚度耐压球壳的临界屈曲荷载呈现近似的线性关系。不同厚度对应的耐压壳临界屈曲压力值下降的幅度值可以作为进一步作为结构敏感性分析的参考因素。因此，观察缺陷幅值较小的0.1～1 mm曲线段，由12组不同厚度t从小到大增加时，临界屈曲压力降低的幅度是逐渐减小的。由此可见，当耐压壳的厚度增加时，其对结构的敏感度是降低的。

图2 耐压球壳缺陷幅值δm与临界屈曲荷载Pcr关系Fig.2 Relationship between imperfection amplitude δm of pressure spherical hull and critical buckling loads Pcr

3.2 厚度半径比对临界屈曲荷载的影响

基于不同的缺陷幅值，建立厚度半径比(t/Rm)与临界屈曲压力值的对应关系，可以量化表达不同尺度耐压球壳对某幅值模态缺陷的敏感程度。同样分析Rm保持不变，球壳厚度t从10～105 mm的12组耐压壳，可以得到相关的临界屈曲压力曲线，为含缺陷的耐压壳设计提供参考。如图3所示，共有10根曲线，每根曲线含有12个计算点。

图3 耐压球壳t/Rm值与临界屈曲压力Pcr的关系Fig.3 Relationship between t/Rm of pressure spherical shell and critical buckling pressure

由图3可知，随着厚度半径比(t/Rm)的不断增大，耐压壳的临界屈曲压力也在呈现斜线增长，且每根斜线间具有相似的斜率和均匀的间距。为进一步细化研究缺陷对耐压壳承载能力的影响，比较相同的厚度半径比时，不同对应缺陷幅值对应的耐压球壳临界压力差值。此处的不同缺陷幅值主要是缺陷幅值为0.1 mm(δ=0.1)和10 mm(δ=10)。图4是上述12组临界压力差值曲线。图4中，纵坐标值ΔPcr即是表示临界压力差值，具体计算表达为ΔPcr=Pcr(δ=0.1)-Pcr(δ=10)，Pcr(δ)为含缺陷幅值为δ的临界压力值。由图4可以得出，临界压力差值曲线大致可以分为3段：在t/Rm<0.033时，随着t/Rm值的增大，ΔPcr值也是逐渐增大且差值幅值较大，结构对缺陷的敏感度是逐渐增强的；在0.033≤t/Rm<0.06时，ΔPcr值随着t/Rm值的增大反而减小，且其降低幅度相对变小，结构对缺陷的敏感度是逐渐减弱的；0.06

图4 t/Rm值对应的临界屈曲压力差值ΔPcrFig.4 Critical buckling pressure difference for different t/Rm of spherical shell

3.3 厚度半径比对临界屈曲荷载相对值的影响

为进一步研究不同的缺陷幅值相对完善球壳的影响，计算不同厚度半径比(t/Rm)得到临界屈曲压力值，并取临界屈曲压力值Pcr与理想完善球壳的弹性屈曲压力值Pperfect的比值Pcr/Pperfect为纵坐标，得到相对值曲线图，如图5所示。

图5 球壳的半径厚度比与相对极限强度的关系Fig.5 Relationship between t/Rm of spherical shell and Pcr/Pperfect

由图5可知，不同缺陷幅值的临界压力相对值走势比较相近，整体上呈现相对值降低的形态。随着t/Rm值的增大，所有相对值曲线的变化率也是在不断减小的。随着缺陷幅值的增大，不同缺陷幅值的比值差值是变小的，且最后均定格在0.15～0.2。一些曲线在t/Rm值为0.015 处出现拐点，反映出结构对缺陷幅值的敏感性存在特殊点，在该点时，相对值取得极大值，这在设计中需要特别引起关注。除此以外，随着厚度的不断增加，耐压球壳对缺陷的敏感性是不断降低的，直至最后缺陷值幅度的影响甚微。

4 结论

1)耐压球壳采用结构的第1阶屈曲模态并非最差初始几何缺陷分布形态。为找到最差的初始缺陷，可以采用结构的前若干阶屈曲模态作为初始缺陷进行比较。然后，采用样本数较大的随机模态法可以合理评估其各阶模态缺陷对应计算结果的可靠度。

2)初始缺陷对耐压球壳有较大的影响，考虑最大幅值为平均半径的1/20的初始几何缺陷后，结构的极限强度最低仅为完善球壳的51%左右。

3)随着缺陷幅值的增大，不同厚度球形耐压壳结构的临界屈曲载荷不断下降，其下降趋势呈现近似的线性关系。如果结构的厚度半径比的逐渐增大，耐压壳结构承载能力会则变得相对稳定，缺陷幅值对其极限强度的影响将逐渐减弱。