当前宏观经济现时预测研究综述

尹德才，张 文

(1.清华大学 社会科学学院 北京 100084；2.西南大学 马克思主义学院，重庆 400715)

一、引 言

现时预测最初被用于气象学领域，世界气象组织的现时预测研究组将其定义为基于当地信息、采用任何方法对当前和未来几小时内天气状况的预测[1]。近年来现时预测被引入经济领域，其基本原理是在官方发布相关统计数据前，尽力挖掘先行高频数据中蕴含的信息、预判当前的经济形势[2]。当前，宏观经济现时预测的可用信息，除传统的统计数据外，还有大量的新型数据，如网络搜索数据、居民支付数据等。丰富的数据资源为更加准确合理地进行预测提供了可能，同时也带来了混频和“维数灾难”等问题。研究者往往采用不同的模型方法解决此类问题。另外，也有学者对若干现时预测模型的预测效果进行比较研究。但总体来看，鲜有文献对现时预测方法进行系统的整理和分析。

正是基于上述背景，本文梳理了国内外有关成果，归纳总结了当前主流的现时预测模型及高维环境下的变量挑选方法，以期为中国学者在大数据环境下更加准确合理地进行宏观经济现时预测提供技术参考。

二、现时预测模型及其效果比较

(一)现时预测模型

当前研究中基于非线性方法的现时预测较少，如Carriero 等(2015)提出的带随机波动项的贝叶斯混频模型，Barnett 等(2016)结合混频多变量状态空间模型与动态因子模型提出非线性动态因子模型现时预测。本文主要介绍作为现时预测主流方法的线性方法，包括：桥方程(BEQ)、混合数据抽样模型(MIDAS)、混合频率向量自回归模型(MF-VAR)以及混频动态因子模型(MF-DFM)。

1.BEQ

BEQ是较早用于处理混频问题的一种方法，许多文献基于BEQ对GDP进行现时预测，如Kitchen等。依据Schumacher(2016)，单变量的桥方程可定义如下：

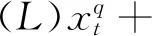
(1)

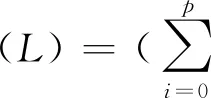
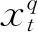
(2)

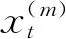
(3)

如果变量为平稳的流量指标，加总函数为：

(4)

2．MIDAS

MIDAS模型最早由Ghysels 等(2004)提出，其灵感源于分布滞后模型。MIDAS模型最初主要应用于金融领域，当前在宏观经济预测中得到广泛应用。

(1)基础的MIDAS模型

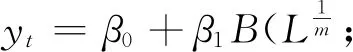
(5)

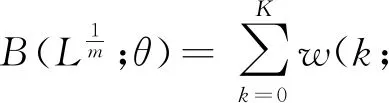
基于式(5)可得相应的预测模型MIDAS(m，K，h)如下：

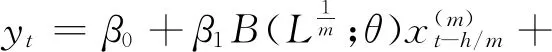
(6)

其中，h为预测步长。若预测目标变量为季度数据，预测变量为月度数据，h小于3意味着基于当前季度的月度数据进行预测，即为现时预测。

(2)AR-MIDAS模型

AR-MIDAS模型是对基础MIDAS模型的自然推广。经济系统惯性的存在，导致宏观经济变量通常具有自相关关系，因此有必要将自回归项引入MIDAS模型。这样得到如下AR-MIDAS模型：

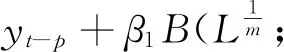
(7)

Foroni和 Marcellino指出，在MIDAS模型中引入被解释变量滞后项会导致模型的有效性受损，而且将导致解释变量间产生季节反应[4]。为消除季节反应，Clements和Galvao(2008)、Foroni等将(1-λLp)引入式(7)，得到如下模型：

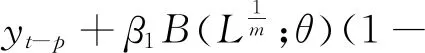
(8)

(3)M(n)-MIDAS模型

宏观经济总量通常受较多变量影响，这意味着对宏观经济的预测需要考虑多个解释变量，上述单变量MIDAS模型都有相应的多变量模型。在上述单变量MIDAS模型前加上“M(n)-”得到相应的M(n)-MIDAS模型和M(n)-AR-MIDAS模型如下：

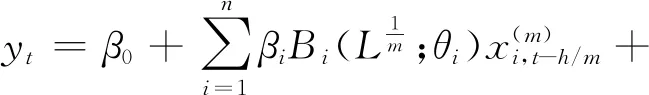
(9)

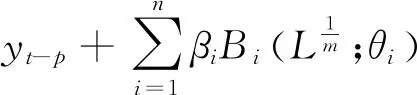
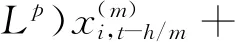
(10)

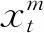
(4)加权函数的设定

权重函数B(k；θ)的选择是MIDAS模型的关键步骤之一，其主要作用有两个：一是将大量的高频数据压缩为较小但又包含大多数信息的数据集，这既可减弱高频数据本身存在的噪音问题，又可避免模型中变量过多存在的共线性问题；二是充分考虑每个高频变量的数据特征并通过权重函数赋予不同的权重值，而并非简单的数据加总后平均，可对高频数据的结构进行分析。目前，常用的几种权重函数形式有三种：Beta分布多项式、指数Almon多项式函数、U-MIDAS (unrestricted MIDAS polynomial)。

Beta分布多项式，主要是通过Beta分布中的概率密度函数来表示权重函数，主要形式如下：

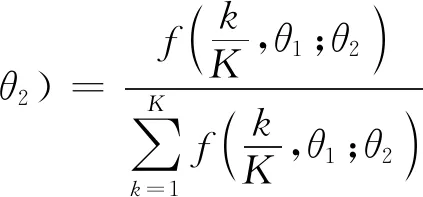
(11)

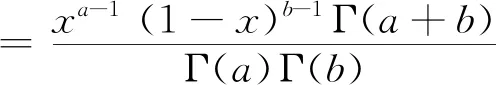
(12)

其中，f(x，a，b)会因为参数的变化而呈现出不同的形式：θ1>1，θ2>1时，为正弦函数形式；θ1<1，θ2<1时，为U型形式；当θ1>1，θ2≤1时，为严格递减函数。

指数Almon多项式函数在当前研究中最常使用。它能构造各种不同的权重函数，既能保证权重为正，又能使方程获得零逼近误差的良好性质[6]。其基本形式如下：

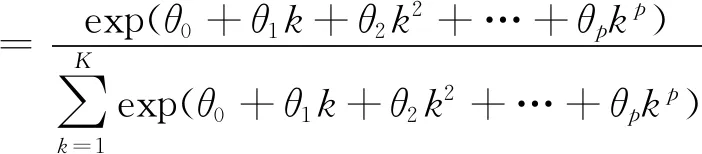
(13)

两参数指数Almon滞后多项式常被用于宏观经济研究中，一般令θ1≤300，θ2<0，以满足宏观经济分析和预测所需的权重形式[7]。U-MIDAS未对系数进行任何限制，多用于频率比值较小的情形。如果所用数据的频率差别较小，比如月度数据预测季序数据，那么U-MIDAS的预测效果更好。

3．MF-VAR

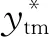
(14)

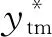
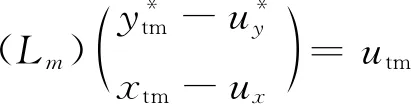
(15)

Foroni和 Marcellino(2014)将最大滞后阶数设定为4并依据BIC准则决定最优滞后阶数p。他们定义stm、ztm如下：

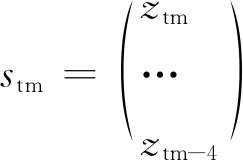
(16)

MF-VAR模型的状态空间形式：

(17)

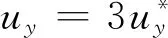
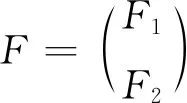
F2=[I808×2]

(18)

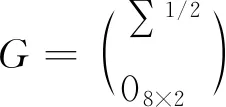
(19)

对于MF-VAR模型的状态空间，可由极大似然估计与EM算法进行估计。由于参数过多时极大似然估计难以得到稳健的结果[4]，通常采用EM算法进行估计。对GDP的预测通常采用卡尔曼平滑方法。关于上述状态空间模型的估计与预测可见Kuzin 等(2011)、Foroni 和 Marcellino(2014)。

4．MF-DFM

自Giannone等(2008)以来，许多学者采用MF-DFM模型进行现时预测，如Rünstler 等(2009)，Rusnák(2016)等。依据Rusnák(2016)，假定xt具有如下因子结构：

xt=Λft+εt

(20)

ft=A1ft-1+A2ft-2…+Apft-p+ut

(21)

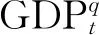
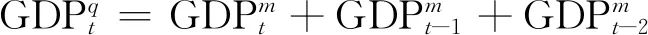
t=3，6，9，…

(22)

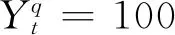
基于式(23)将增长率yt与可观测的GDP数据联系起来：

(23)

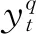
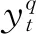
=yt+2yt-1+3yt-2+2yt-3+yt-4

(24)

关于上述模型的估计大致可归结为四步，第一步，估计因子载荷与共同因子；第二步，估计系数矩阵Ai以及系数Λq；第三步，计算ut及其协方差矩阵；最后，基于卡尔曼滤波重新估计因子以及GDP的月度增长率[8]。 具体参考Rusnák(2016)，Bańbura和 Rünstler(2011)等。

5．其他模型

为了利用尽可能多的信息以提高预测精度，部分学者将多种变量选取方法与上述模型结合进而进行现时预测。比如，Marcellino 和 Schumacher(2010)、Andreou 等(2013)将由动态因子模型提取共同因子作为预测变量引入MIDAS模型并提出FA-MIDAS模型，以进行现时预测。另外，作为预测因子的共同因子既可以是低频数据，也可以是高频数据。Kuzin 等(2011)则将共同因子引入MF-VAR进而进行现时预测。

(二)预测效果比较

为找到现时预测的最优方法，部分学者就上述模型的预测效果进行了比较。但到目前为止，学界尚未得出一致结论，甚至某些结论截然相反。比如，Jansen等基于欧盟1996—2011年的月度数据，就MIDAS、MF-VAR、MF-DFM、FA-MIDAS、FA-MF-VAR的现时预测能力比较表明，综合来看DFM是最好的模型[3]。Iizuka也指出混频动态因子模型是现时预测的最好方法[9]。然而，Antipa等利用桥方程和动态因子方程对德国GDP进行现时预测的结果表明，相对于MF-DFM模型，桥方程的预测误差更小，而且通过不断吸纳可利用的月度指标信息，桥方程可以提供更加精确的预测[10]。Marcellino和 Schumacher就德国的GDP进行现时预测，结果表明，一般而言FA-MIDAS模型较相应MIDAS模型有更好的预测效果[11]。Kim 和 Swanson基于U-MIDAS模型和Smoothed MIDAS构建的FA-MIDAS模型对韩国GDP进行现时预测，结果同样表明FA-MIDAS模型较相应的MIDAS模型具有更强的预测能力[12]。

此外，Kuzin等基于欧盟地区20个月度指标，比较了MIDAS模型、AR-MIDAS模型与MF-VAR模型对GDP的现时预测能力后发现，AR-MIDAS模型的预测效果最好，MF-VAR模型的效果次之，MIDAS的效果最差[13]。刘汉和刘金全对比分析了MIDAS类模型对中国宏观经济总量进行预报和预测的准确性和有效性。结果表明，MIDAS模型能有效获取高频数据所携带的信息，在较短的基准预测期内其对GDP的预测效果也更精确，特别是带有自回归项的MIDAS类模型和多变量M(n)-MIDAS类模型的预测效果都要优于不带自回归项和单变量MIDAS模型[5]。然而，基于欧盟大量的月度指标，Foroni 和 Marcellino就桥方程、AR-MIDAS及MF-VAR模型预测能力的比较却指出：综合来看桥方程具有最好的预测效果，对于大部分预测步长AR-MIDAS优于MF-VAR，MF-VAR模型的预测能力最差，对短期预测而言更是如此[4]。

三、信息集与预测变量选取

(一)信息集

宏观经济预测用到的数据可分为三类：传统数据、新兴数据、机器生成的数据。传统数据是高度结构化的调查数据，是公共部门、私人企业为记录、监测它们感兴趣的事件而收集的数据。新兴数据是非结构化数据，来源于社交网络，记录了人类的经历，如存储于博客、视频网站的数据以及网络搜索数据等。机器生成的数据源于物联网，是传感器和机器为测量和记录物理世界中发生的事件和情况而产生的数据。

就现有文献来看，用于宏观经济现时预测的信息集主要为传统数据以及由传统数据构建的指标。但最近几年，越来越多的学者关注新兴数据、机器生成的数据在宏观经济现时预测中的作用。当前宏观经济现时预测所用的非传统数据主要包括如下几类：金融市场数据、电子支付数据、移动电话数据、传感器数据与物联网、卫星图像数据、扫描仪价格数据、在线价格数据、在线搜寻数据、文本数据、社交媒体数据等[14]。

此外，基于非结构化数据进行GDP预测的研究相对较少。部分学者如Aprigliano、Galbraith和Tkacz等率先做出尝试。其中，Aprigliano 等(2017)基于意大利零售结算系统的月度数据，利用混频因子模型分析的预测结果表明，相对于其他的经济周期指标，利用支付数据具有更好的预测效果。Galbraith 和 Tkacz(2018)基于电子支付数据现时预测加拿大的GDP，结果表明基于支付系统数据的预测结果显著地降低了GDP的预测误差，而且借记卡与支票清算数据均提高了预测精度——虽然在有借记卡数据的情况下支票清算数据的价值微乎其微。Liu 等(2018)也探究了在线搜索数据是否可提高中国GDP预测精度。有理由相信，随着大数据技术的发展，基于非结构化数据的研究在未来会取得巨大进步。

(二)预测变量选取

在宏观经济预测中，通常认为包含的变量越多预测的结果越准确，然而模型估计限制使得纳入预测模型的变量数目有限，为此需要挑选变量。常用的变量挑选方法主要包括子集选择法、系数压缩法以及变量降维法。

1.子集选择法

传统的变量选择方法为子集选择法(包括AIC、BIC)，即按照某一准则比较分析待选变量的所有子集或部分子集，然后选出最优的子集。若从p个待选择变量中挑选变量，理论上需要对2p-1个子集进行比较。随着变量个数的增加，全部组合的计算量将庞大到难以接受。此外，子集选择法具有不稳定性，即待选变量集合的微小变化将引起变量选择结果的较大变化[15]。

2.系数压缩法

系数压缩法是当前较为流行的处理高维变量选择的方法，常用的方法包括：LASSO、ENET、Adaptive LASSO。LASSO由Tibshirani(1996)基于Breiman(1995)的Nonnegative Garrote方法提出，通过惩罚函数将回归模型中部分变量的系数压缩为零，从而实现变量选择。具体的LASSO通过解决如下最小化问题进行变量选择：

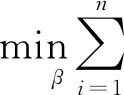
(25)

其中，λ为调整参数，它控制惩罚的强度。

LASSO适用于“真实”模型中含有许多零系数的情形。但如果预测因子有较强相关性，LASSO的预测效果可能不如岭回归[16]。Zou 和 Hastie将LASSO与岭回归相结合提出ENET，它具有LASSO和岭回归的优势，不但能够选择变量，而且能够处理成组的强相关变量[17]。该方法通过解决如下目标函数实现变量挑选：

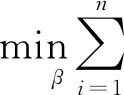
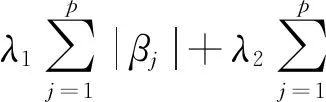
(26)

其中，λ1和λ2均为调整参数。

3.变量降维法

变量降维法主要包括偏最小二乘法、因子分析等方法。关于偏最小二乘最早见于Wold(1966)，此处主要简要介绍动态因子分析的估计。动态因子模型可以从高维数据中提取少量的包含丰富信息的共同因子，从而实现高维数据的降维。这些共同因子可用于预测、构建指数等，近十几年来动态因子模型在宏观计量经济学中得到广泛应用。动态因子模型具有如下形式：

Xt=λ(L)ft+εt

(27)

ft=A1ft-1+A2ft-2…+Apft-p+ut

(28)

其中，Xt(t=1，2，…，T)为N维向量，λ(L)为N×q阶滞后多项式矩阵，ft=(f1t，f2t，…，fq t)为共同因子，ut为异质性冲击向量，Λ为因子载荷矩阵，Ai(i=1，2，…，p)为因子的自回归系数矩阵。

Xt=ΛFt+et

(29)

Ф(L)Ft=Gηt

(30)

上述两式称为动态因子模型的静态形式。Bai和Ng指出，从预测的角度看，静态因子模型和动态因子模型的效果几乎没有差异[18]。

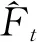
关于因子个数r的估计，Bai和Ng提出如下信息准则[19]：

(31)

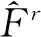
(32)

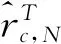
此外，Bai和Ng提出一种不需要估计动态因子就可估计动态因子个数的方法[18]。上述关于动态因子模型的估计均是在变量平稳的假定下进行的，关于非平稳下共同因子的估计可参见Stock 和 Watson(2011)与Barigozzi等(2016)。

四、中国宏观经济的现时预测状况

鉴于中国经济的快速发展及其对全球经济发展的重要影响，近年来国内外学者开始对中国GDP进行现时预测。Yiu和Chow(2010)、Barnett和Tang(2016)利用因子模型现时预测中国GDP增长率。Yiu 和Chow发现因子模型较随机游走模型预测能力更好，而且就中国GDP的现时预测而言利率是最重要的变量，居民消费和零售价格指数以及固定资产投资也有较大影响[21]。Barnett 和 Tang计算Divisia货币指数同时结合其他宏观时间序列数据现时预测中国的月度GDP数据，结果表明Divisia货币加总较简单的加总包含更多的指标信息，提高了因子模型的预测效果[22]。陈磊等采用混频动态因子模型(MF-DFM)对中国季度环比GDP增速进行实时预测。结果表明，物价、进出口和工业生产等统计指标能够以较大的幅度降低预测误差，货币供应量等金融指标对预测精度的改善相对较小，PMI等调查数据几乎没有改善预测精度[23]。

刘金全等结合中国宏观经济混频数据，使用蒙特卡洛模拟对MIDAS模型的有效性进行了分析并指出：MIDAS模型的效果要受到样本长度、滞后阶数、信噪比以及数据本身内在特征的影响，它在用于预测中国宏观经济时是有效的——但效果会受到中国宏观经济数据的样本长度和模型优化后的权重函数形式的影响[24]。刘金全和刘汉检验了MIDAS模型特别是带有自回归项和多变量MIDAS模型在预测中国GDP时的有效性。其研究结果还表明，金融危机背景下，“三驾马车”中出口对宏观经济的影响要大于消费和投资，后两者对GDP具有较长时期的影响；在预测实际GDP时，三者的短期影响更大[5]。此外Jiang等采用FA-MIDAS方法基于价格指数等44个月度宏观经济指标以及人民币汇率等54个日度金融指标，预测了中国季度GDP。结果表明，FA-MIDAS方法较传统的方法——加总得到高频数据的低频数据，然后利用OLS方法进行预测——更加有效[25]。可以发现，上述研究有三个重点：一是利用中国实时数据探究宏观经济现时预测方法的效果，二是利用现时预测方法寻找影响中国宏观经济的关键因素，三是对短近时期中国GDP增长进行预测。这其中的核心问题就是寻找到适合对中国宏观经济进行现时预测的最佳模型方法。但由于模型方法和指标选择各不相同，既有研究的结论也有较大差异。

五、结 语

宏观经济现时预测能够为决策者提供更及时更准确的经济预测，帮助其有效地应对市场波动，因此在近年来成为新兴的学术研究热点问题。本文对当前国际上主流的宏观经济现时预测方法桥方程、混合数据抽样模型、混合频率向量自回归模型和混频动态因子模型等做了一个比较全面地介绍。在此基础之上，介绍了目前主要的数据信息以及预测变量的选取方法如子集选择法、系数压缩法和变量降维法等。最后对当前中国宏观经济现时预测研究现状作了简要阐述。

结合前述分析，本文认为现有研究还存在如下不足，这也是未来研究的主要方向。

第一，关于不同模型的预测能力。就本文所列现时预测模型而言，尚不能确定哪种方法具有最好的预测效果。相同的两种方法，基于不同甚至同一地区的数据，可能得出不同的结论。排除研究模型的使用有误外，信息集和变量挑选方法的差异为重要原因。因此，在研究中应充分比较预测模型、变量挑选的不同组合，以获得更精确的预测效果。

第二，预测过程中传统数据与非传统数据的有效利用问题。传统数据与非传统数据各具特点，前者噪音少，但频率低，难以提供经济形势的实时信息；后者噪音高，但频率也高，可提供经济形势的实时信息。这种情况下，如何充分利用两种数据的优势同时克服其局限，以得到更为精确的预测结果就显得尤为重要。然而，现有文献或者侧重对非传统数据的挖掘应用，或者对两类数据不加区别地利用，鲜有文献探究预测两类数据的有效结合问题。

第三，关于线性与非线性预测模型。现有文献大多采用线性模型预测宏观经济形势，采用非线性方法的较少。采用线性预测方法，意味着假定经济结构不发生变化，但现实并非如此，尤其是在后发国家。诚如Balcilar 等(2015)指出，与发达国家相比，新兴市场和转型经济体面临的更大的挑战之一就是政策制度改变造成的结构变化。这意味着基于非线性方法的现时预测可能具有更高的预测精度——特别是在制度不完善或不稳定的经济体。

第四，关于中国宏观经济的现时预测。关于中国宏观经济形势现时预测的文献相对较少，所用数据主要为传统数据，所用模型主要为线性模型。为更精确地对中国宏观经济进行现时预测，就要综合运用多种模型多方数据，不仅要利用线性模型还要利用非线性模型，不仅需利用传统数据还需利用非传统数据——难点是如何实现两类数据的有效结合。

宏观经济现时预测具有重要的理论和实践意义，而大数据时代为其提供了海量数据支持。这种情况下如何更好地进行现时预测为公共政策制定和企业决策提供服务，就成为经济研究者面临的重要问题。研究课题的重要性与当前研究滞后的现实，要求我们必须大力推进相关研究，寻找到最适合中国国情、最有助于解释，预测中国宏观经济发展的理论方法。