基于能量范数成像条件的一阶方程弹性波逆时偏移

蔡志成,顾汉明,曹静杰

(1.河北地质大学勘查技术与工程学院,河北石家庄050031;2.中国地质大学地球物理与空间信息学院地球内部多尺度成像湖北省重点实验室,湖北武汉430074)

逆时偏移(RTM)技术相对其它偏移方法具有成像精度高的优势[1-3],能够处理速度横向变化剧烈、陡倾角构造等复杂地质情况[4]。近年来,随着计算机技术的快速发展,RTM方法逐渐走向实用化[5-7]。基于弹性介质假设的逆时偏移方法在理论上考虑了实际介质中波传播多波多分量问题,能得到较为准确的成像结果,因而备受关注。

弹性波逆时偏移问题的研究主要包括震源、检波点波场重建和成像条件应用。不少学者在弹性波RTM过程中先进行纵横波波场分离然后再成像[8-10]。采用的主要方法是基于Helmholtz分解的波场分离[11],可分为直接波场分离法[12-14]和间接波场分离法。直接波场分离法是在空间域对波场进行散度和旋度运算分离得到纵、横波波场,但存在振幅相位校正问题。AKI等[15]选择空间域矢量分解方法解决了成像时极性反转问题,但其波场的物理意义发生了改变;ZHU[16]尝试在波数域进行波场分离,但该方法需要进行数据域转换以及波数域归一化处理等才可保证其物理意义。间接波场分离技术则是改造波动方程,在波场延拓过程中分解得到纵横波分量。马德堂等[17]利用各向同性介质纵横波分离方程实现波场完全分解。XIAO等[18]通过纵波方程得到纵波波场再与弹性波波场作差得到分离的横波波场,此类方法能够得到与原波场一致的纵横波波场。WANG等[19]将基于纵横波矢量解耦的波动方程应用于弹性波逆时偏移成像,得到独立的纵横波偏移结果。吴潇等[20]对比了5种波场分离方法在弹性波逆时偏移中的应用效果。与直接波场分离法相比,间接波场分离法成像质量更好,但这类方法需要改造波动方程,增加了计算量和内存存储。

应用准确成像条件是弹性波逆时偏移成像的关键环节。激发时间成像条件是利用提取震源与检波点波场对应成像时间波场值,得到最终偏移结果[21-22];还有通过提取震源、检波点波场作比值进行成像[23-24]。该类方法计算效率高,且有一定的保幅特性,但转换波成像物理意义有待研究。较为常用的互相关成像条件能够利用全波场信息,有学者通过选择性成像[25]和滤波的方法压制背向散射噪声干扰[26],但该压制技术同时也会对有效信号造成损伤。ROCHA等[26-27]利用弹性波波动方程及能量守恒原则,提出新的成像条件,成像结果表示反射系数能量,无需对整个波场进行纵横波分离,也避免了极性反转等传统弹性波偏移成像的问题。张晓语等[28-29]在ROCHA等提出方法的基础上发展了基于能量密度自解耦成像条件,此成像条件能够有效压制低频散射成像干扰,主要应用了二阶方程,对于具有较高效率的交错网格一阶方程尚无具体实现方式。本文发展了一阶速度应力弹性波能量范数成像条件的逆时偏移方法,通过构造中间应变量给出了一阶方程情况下各分量转换规则,提出了具体波场更新方式。最后通过数值算例测试了该方法对弹性波逆时偏移中低频噪声的压制效果。

1 方法原理

1.1 弹性波逆时偏移理论

逆时偏移理论框架可按其实现步骤来描述:①震源波场正向外推;②检波点波场逆时延拓;③成像条件应用。震源波场正向外推可简化为如下边值问题[1]:

(1)

式中:Us(x,z,t)为震源波场值;f(t)为加载震源函数。波场值更新采用数值离散化的波动方程求取。检波点波场逆时延拓则与正向外推相反[1],可表达为:

(2)

式中:g(t)为地震记录值;Ur(x,z,t)为检波点波场值;Tmax为最大记录时间。公式(2)中将检波点地震记录作为初始条件,利用波场延拓算子求取进行逆时延拓。逆时偏移是记录每一计算递推时刻的震源波场和检波点波场,然后选取相应成像条件得到最终偏移剖面。

本文方法基于完全弹性假设,波场延拓过程采用各向同性介质一阶速度应力弹性波方程[3]:

(3)

式中:σxx、σzz、σxz为应力分量;vx、vz为速度分量;vP、vS分别为介质中纵、横波速度;ρ为密度。本文采用伪谱法对此方程进行数值离散。

1.2 能量范数成像条件

逆时偏移中常用的互相关成像条件[3]表达为:

(4)

式中:I为成像结果;Us为震源波场;Ur为检波点波场;e表示炮索引号;t为时间。在应用该成像条件时,存在检波点波场与震源波场相同路径传播的互相关噪声。

能量范数成像条件首先从能量角度以一维方程声波定义一个空间域(Ω)内能量表达[26]:

(5)

式中:U为波场值;v为介质中波速。定义波场能量范数为:

(6)

类似两个波场U、V的内积能量范数可表达为:

(7)

借助(4)式,U、V为正反传波场时,能量范数成像条件[26]为:

(8)

在弹性介质假设条件下,公式(8)中两个波场对应为弹性波场。

1.3 能量范数成像条件噪声压制分析

下面进一步分析上述成像条件噪声压制原理。将检波点波场与震源波场看作是多方向的平面波合成,分别将震源和检波点波场变换至频率域,互相关成像条件可以表示为:

(9)

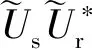
(10)

式中:ks、kr分别为震源波场和检波点波场的波数向量;θ为波场波数向量夹角。利用频散关系:

(11)

得到能量范数成像条件[26]为:

(12)

在ω2项前加入一个cos2θc项,将其近似表示为:

(13)

当选择θc与θ相等时,则该夹角的能量范数为0,将其反变换回空间域可以得到:

(14)

因此,可以选择θc来压制震源波场与检波点波场任意角度互相关造成的干扰噪声。互相关成像条件的后散射干扰可以近似看作两个波场成180°互相关干扰,这里设置θc为90°入射,即得到最终压制反向散射干扰成像条件为:

(15)

将其应用于二维弹性波逆时偏移成像中得到垂直分量和水平分量成像条件:

(16)

(17)

式中:(IE)x、(IE)z分别为能量范数成像条件偏移结果的水平分量和垂直分量;Usx、Usz分别为震源波场x分量和z分量;Urx、Urz分别为检波点波场x分量和z分量。

1.4 能量范数成像条件弹性波逆时偏移

公式(16)和公式(17)利用一阶速度应力弹性波方程求取时需引入中间变量,首先假设:

(18)

对(18)式取时间一阶导数,变换得到:

(19)

由(19)式假设的中间分量可以通过速度分量空间偏导求取,对(19)式利用时间二阶差分和空间伪谱法进行数值离散,有:

(20)

1.5 伪谱法数值离散求解方式

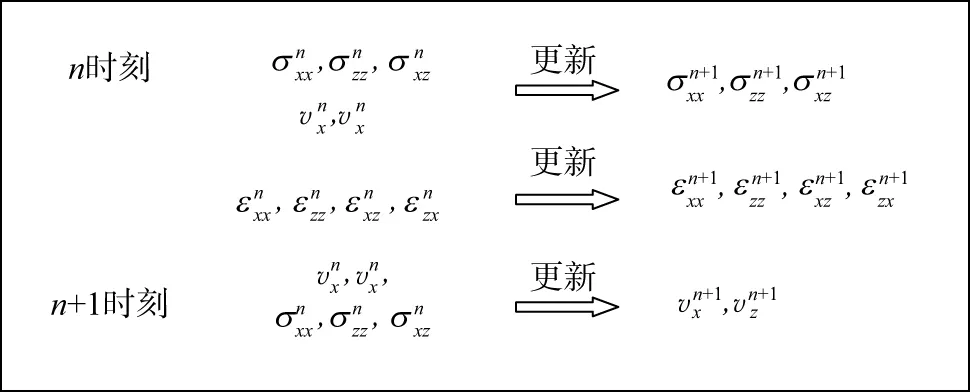
图1 能量反射成像条件一阶弹性波逆时偏移各分量更新示意

2 模型试算分析

为验证算法正确性,设计两层介质模型进行试算分析,模型参数如图2所示,密度由一般经验公式计算得到。对单炮正演得到地震记录进行偏移,震源采用30Hz雷克子波,位置为(1000m,0);201道接收,道间距10m,检波点深度为0,0.5ms采样,1.0s记录长度。

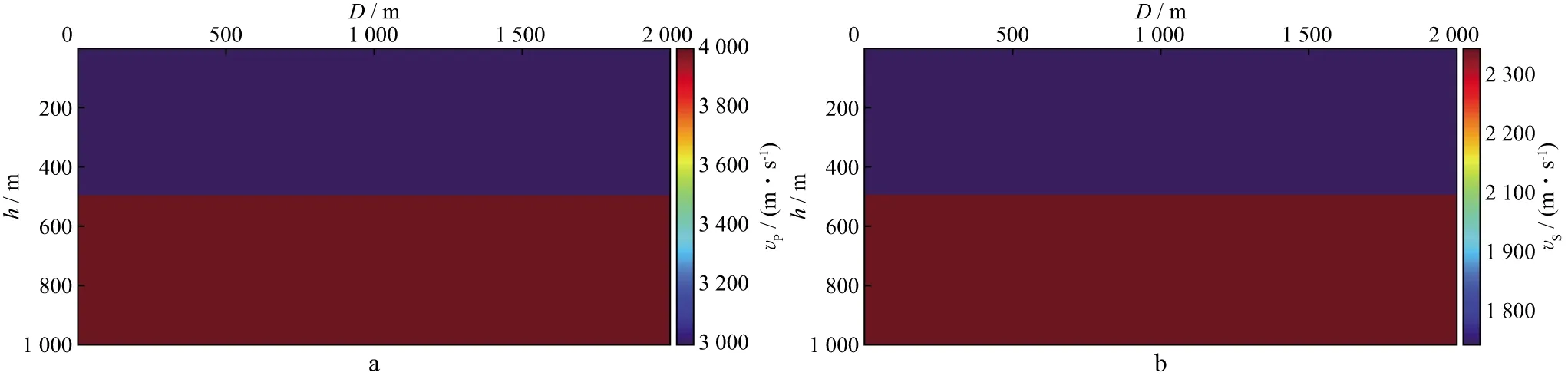
图2 两层模型速度参数a 纵波速度; b 横波速度

图3为利用伪谱法弹性波互相关成像条件和能量范数成像条件对单炮记录进行偏移的结果。从图3a 和图3b可以看出,由于直达波近似水平方向传播与检波点波场绕射产生的P波和S波产生的干扰被较好压制(箭头处),在界面上方的大部分绕射产生的干扰很大程度上得到了消除;从图3c和图3d可以看出,椭圆部分低频噪声部分被压制。多炮偏移叠加结果如图4所示。从图4a和图4b可以看出,界面上方的低频散射干扰明显降低;图4c和图4d验证了能量范数成像条件的有效去噪效果。

图3 伪谱法弹性波互相关成像条件和能量范数成像条件单炮记录偏移结果a vx分量互相关成像条件偏移结果; b vz分量互相关成像条件偏移结果; c 能量范数成像条件x分量偏移结果; d 能量范数成像条件z分量偏移结果

图4 伪谱法弹性波互相关成像条件和能量范数成像条件多炮偏移叠加结果a vx分量互相关成像条件偏移结果; b vz分量互相关成像条件偏移结果; c 能量范数成像条件x分量偏移结果; d 能量范数成像条件z分量偏移结果

设计凹陷模型(图5)进行多分量逆时偏移试算,分别测试互相关成像条件的偏移、纵横波解耦的弹性波偏移、能量范数成像条件的弹性波逆时偏移和多炮偏移叠加结果,如图6所示。与直接利用vx、vz分量进行互相关成像(图6a,图6b)相比,基于纵横波分离的成像PP波与SS波偏移结果更为清晰,第二界面上方的低频干扰明显降低(图6c,图6f)。PS波与SP波的偏移效果则较差(图6d,图6e),说明不同类型波场的直接互相关成像方法带来了更多噪声,甚至有效信息被覆盖,而关于转换波的成像方法则还需要利用其它技术来完成。基于能量范数成像条件的偏移结果x分量与z分量存在的低频噪声明显降低(图6g,图6h),正反传波场的非界面处互相关噪声得到了较好的压制。

图5 凹陷模型速度参数a 纵波速度模型; b 横波速度模型

图6 凹陷模型弹性波多炮偏移叠加结果a vx分量互相关成像条件偏移; b vz分量互相关成像条件偏移叠加; c 纵横波波场分离PP波偏移多炮叠加; d 纵横波波场分离PS波偏移多炮叠加; e 纵横波波场分离SP波偏移多炮叠加; f 纵横波波场分离SS波偏移多炮叠加; g 能量范数成像条件x分量偏移多炮叠加; h 能量范数成像条件z分量偏移多炮叠加

3 复杂模型试算

截取Marmousi模型的一部分进行本文方法的噪声压制测试,模型大小为2000m×700m,网格大小5m×5m,速度参数如图7所示,密度由一般经验公式计算得到。正演模拟共41炮,炮点位置从0到2000m,炮间距50m。单炮401道接收,道间距5m,分布于整个模型地表附近,0.5ms采样,2s记录长度。炮点、检波点深度均为0,采用30Hz雷克子波点震源(同时激发纵波和横波)。从最终偏移叠加剖面(图8)可以看出,与互相关成像条件偏移结果(图8a,图8b)相比,基于能量范数成像条件的结果(图8g,图8h)中低频噪声得到了较好的压制;与纵横波分离后的成像结果(图8c,图8d,图8e,图8f)相比,图8g和图8h的信噪比较高。

图7 复杂模型速度参数a 纵波速度模型; b 横波速度模型

图8 复杂模型弹性波多炮偏移叠加结果a vx分量互相关成像条件偏移多炮叠加; b vz分量互相关成像条件偏移多炮叠加; c 纵横波波场分离PP波偏移多炮叠加; d 纵横波波场分离PS波偏移多炮叠加; e 纵横波波场分离SP波偏移多炮叠加; f 纵横波波场分离PS波偏移多炮叠加; g 能量范数成像条件x分量偏移多炮叠加; h 能量范数成像条件z分量偏移多炮叠加

4 结论

本文从能量范数的角度详细分析了能量范数成像条件及其噪声压制原理,将这一成像条件发展到了一阶速度应力弹性波逆时偏移方法中。通过引入中间应变分量进行所需分量更新,实现了一阶速度应力弹性波方程逆时偏移方法能量范数成像条件的应用。通过复杂模型试算,对比vx分量、vz分量互相关成像条件偏移结果,本文方法能够压制低频噪声;对比纵横波波场分离偏移,本文方法无需考虑转换波极性反转问题,避免进行解耦波动方程延拓。