“析”运算能力障碍 “寻”培养能力途径

叶燕华

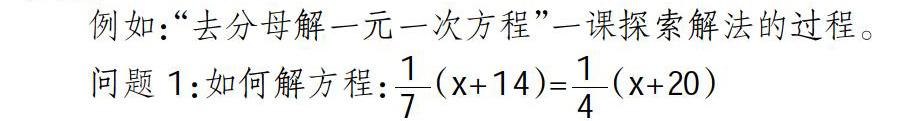
【摘 要】运算能力是课标关注的核心能力，是学生数学学习的“童子功”，也是学生数学学习的重要基础。但初中生普遍存在“运算能力障碍”。为了提高学生的数学运算能力，教师应深入分析学生的运算错误原因，针对学生实际，引导学生重视基础、明算理、讲算法，细观察、勤思考，培养学生的思维能力，提高学生的运算能力。

【关键词】数学运算能力;障碍;途径

运算能力是初中数学的基本能力，运算能力对学生数学学习质量起关键作用。因此，在中小学数学的教学中，教师都十分重视对学生运算能力的培养。尽管如此，运算问题仍是初中生在学习中遇到的最大障碍之一，经常出现运算速度慢、计算准确率低，在考试中数学成绩甚至于物理、化学成绩都不理想的现象。而不少教师和学生对运算能力的理解不到位，常常将运算过程中的错误原因归结为学生的“粗心大意”“机械照搬公式”“盲目演算”等，究其深层原因，是学生的思维模式、学习方法及教师的教学方法未能达到灵活运用运算能力的要求。因此，深入分析学生在数学学习中的运算能力障碍，针对学生在运算过程中所暴露的问题，找出解决方法，才能尽可能地提高学生的数学思维能力。

1.初中生数学运算能力障碍分析

1.1学生不重视对基本概念的理解与掌握

从学生的答题情况和得分数据分析来看，学生对数学基本概念、公式的运用掌握得并不尽如人意。学生在运算过程中，往往是某个环节出现了问题，如数学概念不清、运算公式记错、解题基本方法掌握不充分等，导致整个运算的错误。

1.2学生不重视算理算法的学习过程

例如，2016年漳州质检卷第8题：若-2a<-2b，则a>b，其根据是（    ）

A.不等式的基本性质1   B.不等式的基本性质2

C.不等式的基本性质3   D.等式的基本性质2

本题考查不等式的基本形式，不仅要学生会解不等式，还要了解每一步的理由依据。在考后的试卷分析中，出人意料的是：此“送分题”变成了“送命题”，很多学生答错。学生在学习过程中，教师比较重视对其运算技能的训练，采用题海战术，进行大量的机械性练习，但不重视培养学生发现、推导、证明运算法则的能力，学生缺乏对算理的理解，仅是机械性地选择算法，虽然在一定程度上形成了技能，但并没有真正提高学生内化算法算理的能力。

2.培养学生运算能力的途径

2.1夯实基础知识，确保运算的准确性

《课标》指出：“运算能力是指能够根据法则和运算律正确进行运算的能力。”能否准确理解和灵活掌握各种运算所需的数学概念、运算公式、法则，以及学生是否对数学概念、运算公式、法则的理解深刻，都直接影响到算法的选择与运算准确度。如果数学概念模糊，运算公式、法则混乱，必定会影响学生的运算能力。为了提高学生的运算速度，确保准确率，教师在平时的教学中，可以让学生先从概念、性质、公式和法则的理解入手，着重掌握好有关运算的基础知识和基本技能，提高解题的准确性。

2.2重视算理、算法，保证运算的合理性

运算的合理性是运算能力的核心。它要求运算过程要符合算理，每一步都应有理有据。这就要求学生明算理，合理地寻找最佳运算途径。如一个法则的推导，得出过程通常包含对概念的理解、方法的概括归纳及数学表达，这是一个思维训练的过程，是运算合理性的表现。在推导中有时还会出现一题有多种不同的运算途径，繁简不同，则需加以比较，选择最佳解法、最优算法。因此，在平时教学中，教师要让学生在弄懂、弄通必要的算理、算法、算律上多下功夫，同时注重培养学生一题多解的能力，讲究算法，鼓励学生对一道题进行多角度、多方位的探索，逐步达到合理算法、提高运算能力的目的。

例如：“去分母解一元一次方程”一课探索解法的过程。

学生活动：限时让学生独立解答，多数学生会利用学习过的去括号法解方程。

问题2：同学们在完成哪一步时花的时间较多？是否有更简便的方法呢？

（教师提示：与上节课所学不同的是这个方程的系数是分数，不好计算，还容易出错，大家是否有办法把分母去掉，将分数化为整数？）

教学分析：在教师的提示下，让学生大胆尝试，想办法在已有知识的基础上，化未知为已知，化繁为简，让学生体会转化的数学思想，学会选择最优算法。

师生活动：学生展示交流，讨论如何解含分母的一元一次方程。

问题3：解法依据是什么？

教学分析：以此问题强调解方程的每一个步骤都需要有理有据，教师在教学过程中，培养了学生明算理、讲算法的数学运算能力。

本节内容其实没有新知识，关键是培养学生的运算能力，使其通过对算理算法的思考，深刻理解解方程的新方法。教学中讲究算法，扬长避短，减少出错的机会，尽量以最短的时间得到正确的结果，这样又能培养学生的算理能力，在不断比较、选择中，学生在多解的思路中选择的合理解法，明确算理。

2.3深入思考，培养运算的灵活性

在很多情况下，数学运算是在一定情境中进行的，结合具体情境抽象出运算对象是解决问题的首要任务，结合情境探索运算思路是解决问题的关键。因此，教师需要在研究常规算法的基础上，深入研究非常规算法，使学生学会选择适当的运算方法，灵活设计运算程序，成功解答。这一过程不仅是要培养学生的运算能力，还需培养学生数学思考和问题解决的思维能力。

例如，在“运用平方差公式因式分解”的教学中，教师设计了这样一道具有挑战性和新颖性的题目：设a=192×918，b=8882-302，c=10532-7472，则a，b，c的大小关系是   。在解题过程中，大部分学生纯粹计算，结果耗时费力且正确率还不高。但若能深入思考就能发现，第二和第三两项可以利用平方差公式进行因式分解：

b=（888-30）（888+30）=858×918，

c=（1053-747）（1053+747）=306×1800=306×3×600

=600×918，a=361×918所以a

再如，已知x2-x-1，求x4-3x2的值。如让学生先解方程再直接代入求值，会比较繁琐。对此，教师可引导学生构建新的算法，结合解一元二次方程的降次转化思想，得到x2=x+1，x4=x2+2x+1=x+1+2x+1=3x+2，于是x4-3x2=3x+2

-3（x+1）=3x+2-3x-3=-1。

根据以上例子可以看出，题目的非常规解法通常是来源于对原题结构的思考，同时进行相应的解构和重建构，则解题具有较强的灵活性与技巧性。所以，在平时教学活动中，教师要经常和学生一起探索问题的非常规解法，深入观察分析运算对象，提高学生的运算能力。

运算能力培的养是一个长期的过程，教师在教学中要认真倾听学生的思考过程，及时发现学生运算错误的原因，有针对性地加强学生对运算意义的理解，不仅教会学生计算，还要使学生明算理、讲算法，注重数学思考与问题解决，让学生学会选择适当的运算方法，优化运算过程，只有这样，才能有效发展学生的运算能力。

【参考文献】

[1]徐建.关注运算能力，培养核心素养[J].中学数学参考（中旬），2018（8）：64-66

[2]楊九诠，李铁安.义务教育课程标准（2011年版）案例式解读（初中数学）[M].教育科学出版社，2012：30-34

（本论文系2018年度漳州市基础教育教学研究课题 《学科交叉条件下的初中生运算能力培养探究》，立项批准号：ZPKTY18024。）

（福建省漳州市第五中学，福建 漳州 363000）