拟周期复合材料结构的双尺度有限元误差分析

李志青LI Zhi-qing；蓝光进LAN Guang-jin；冯南飞FENG Nan-fei

（广东财经大学华商学院，广州511300）

0 引言

材料是科学技术发展的重要基础，在新材料的开发利用过程中经常需要对一类具有拟周期结构复合材料进行分析。这些复合材料由于系数局部变化很大，已经有很多的学者和专家用均匀化方法研究了该类问题，文献[1-5]，曹、崔、冯和张等分别研究了三维编织复合材料等效力学参数的双尺度计算和拟周期复合材料结构的二阶双尺度渐近分析以及具有小周期结构复合材料热力耦合问题的多尺度分析及双尺度有限元算法；但他们均是对于一般区域中热力耦合现象的数值模拟与计算方法的讨论，对于拟周期结构复合材料热力耦合问题的有限元解问题以及它的有限元误差估计分析还是很少人讨论。关于拟周期复合材料结构的热力耦合动态问题可表述为以下的微分方程组：

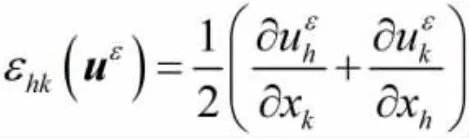
具有拟周期复合材料结构的热力耦合的瞬态问题精确解和数值解是非常困难，为了简化问题，我们仅考虑具有Dirichlet 边界的稳态问题，所以假设

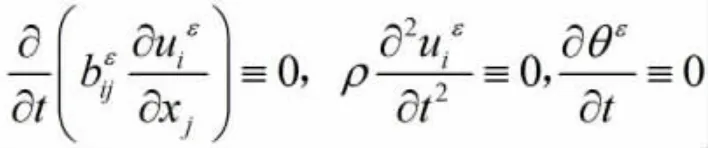
通过上述假设，把ρbi和放在一起考虑，那么问题可以重新写成下面两个子问题：

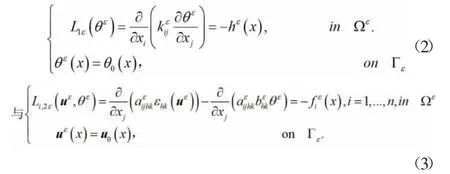
其中：

1 均匀化方程及的、双尺度渐近展开

假设问题（2）有如下的双尺度形式渐近解：

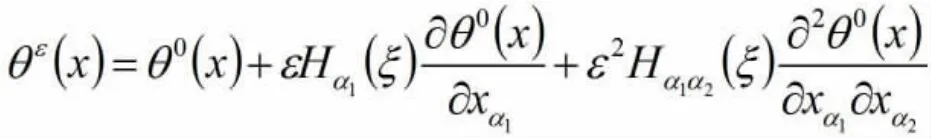
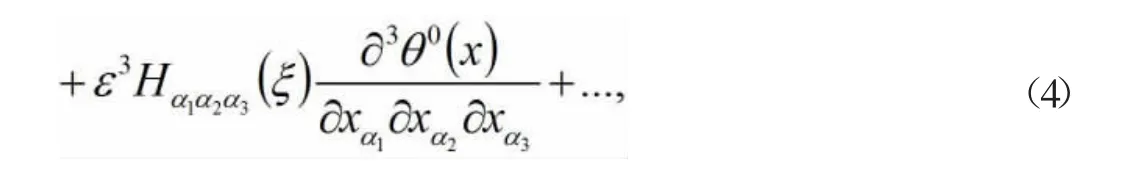
假设Hα1（ξ），Hα1α2（ξ），Hα1α2α3（ξ）…都是定义在整个空间Rn上，且都是关于ξ 为周期的函数，它们均在单胞Q 上定解。

将式（4）代入方程组式（2）中，根据ε 的任意性，通过认真计算且比较ε-2，ε-1，ε0，ε1，…对应的边界条件和两边系数后，可得Hα1（ξ）、Hα1α2（ξ），可由下面问题定解：

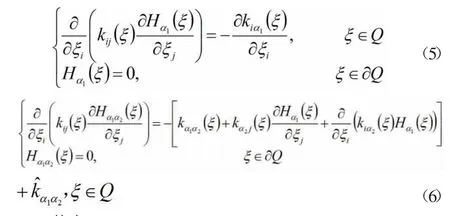
其中：

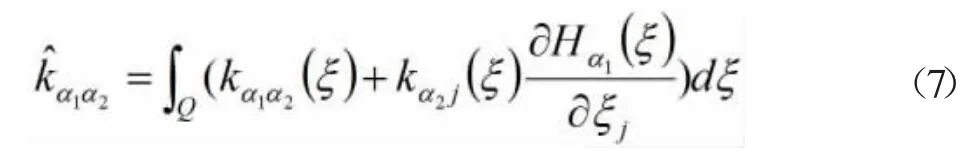
θ0（x）为对应问题（2）的均匀化解，其满足如下的常系数均匀化方程：

其中：

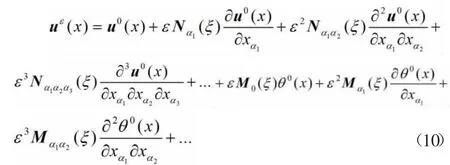
将式（10）代入方程组式（3）中，根据ε 的任意性，通过认真计算且比较ε-2，ε-1，ε0，ε，…的边界条件及两边系数后，可得和可由下面微分方程定解：

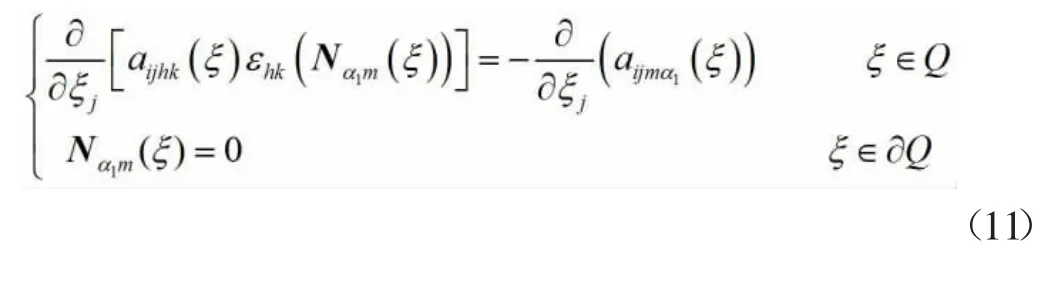
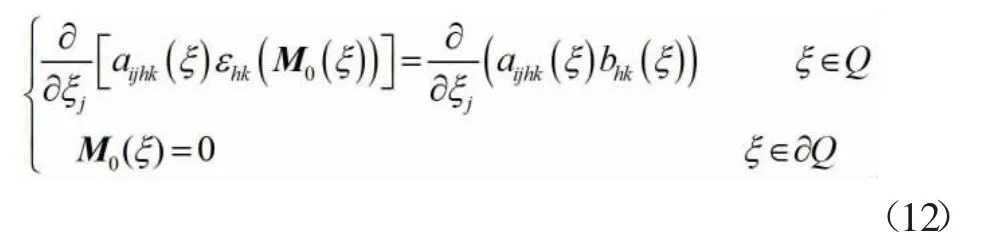
其中：

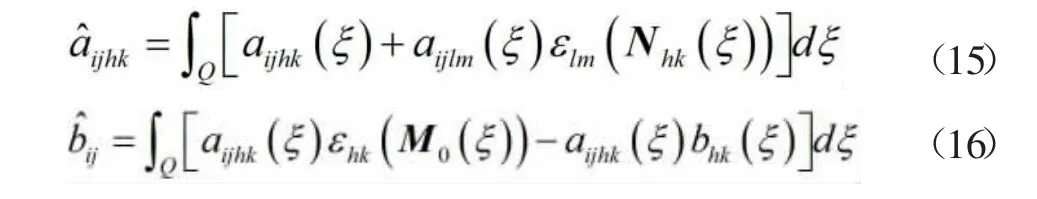
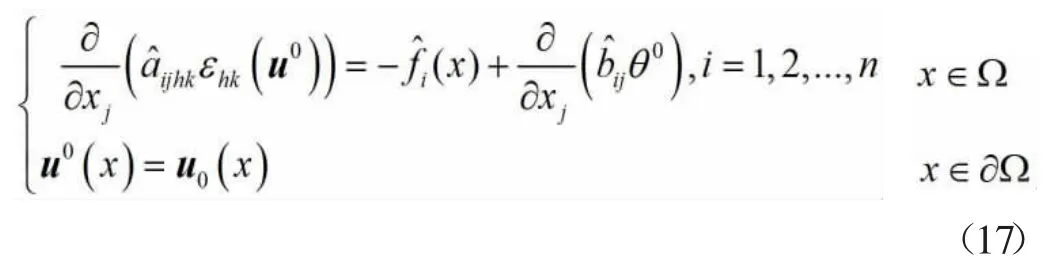
2 有限元误差估计分析

在Q 和Ω 中，我们引入两个函数空间：

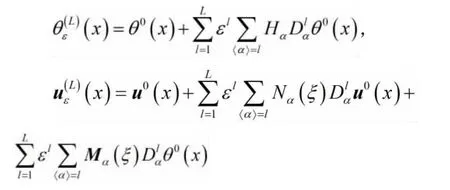
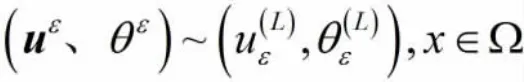
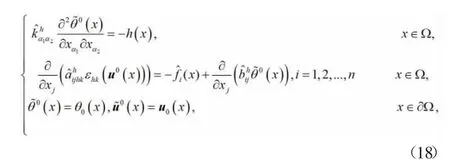
其中：

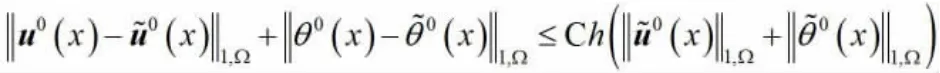
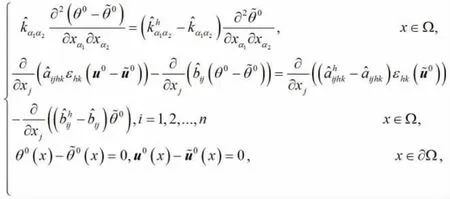
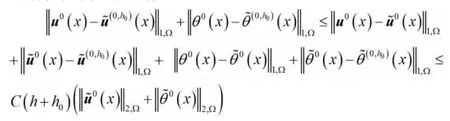
定理2.3：假设Ω 是具有Lipschitz 边界的有界区域，是问题（1）的弱解，是其L-阶双尺度有限元渐近解，，，

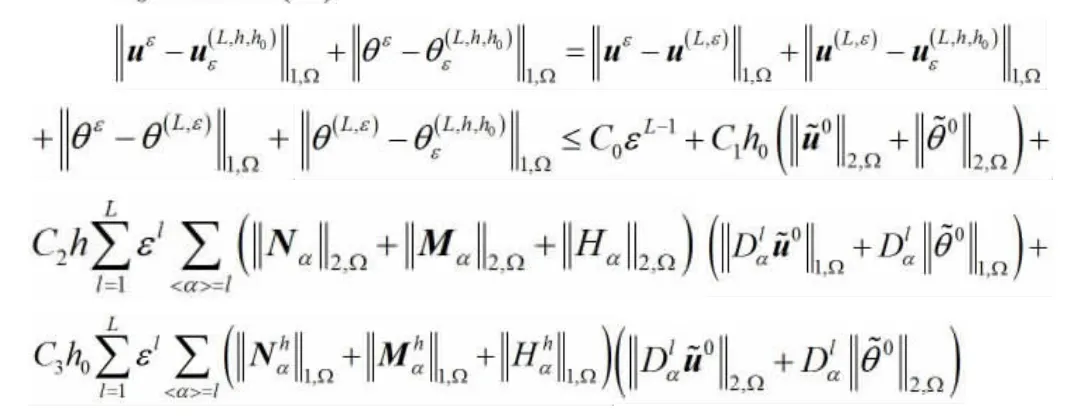
成立。当L=1 时，有以下估计式成立：

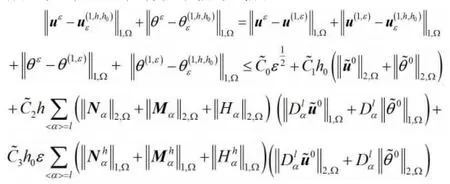
其中Ci和是与ε 无关的正常数。

定理2.2 和定理2.3 的证明类似于定理2.1 的证明方法和技巧。

3 双尺度有限元算法过程

①确定材料或区域属性，特别是小周期内的各种材料的构成；②计算标量函数，矩阵函数和向量函数的有限元解；③计算对应的均匀化系数；④计算相对温度增量和位移矢量的均匀化解与；⑤计算；⑥得到相应的有限元误差估计式。

4 小结