飞机导航系统中多套惯导融合方案仿真分析研究
2020-02-05白俊强刘成茂
白俊强,昌 敏,汪 辉,郭 彬,刘成茂
(1.西北工业大学无人系统技术研究院,西安710072;2.西安索格亚航空科技有限公司,西安710065;3.西北工业大学航空学院,西安710072)
1 引言
对于民航飞机导航系统领域,多传感器耦合导航已成为主流导航方法。通过多传感器之间的信息融合,如何有效利用和处理来自多套传感器系统的数据,克服单一传感器导航模式的不足,达成提高导航精度、增强导航系统的可靠性的目的,是多传感器系统需要首要关注的问题之一[1-3]。
不同客机上配备的导航系统形式与数量各有不同,其中最为常用的是惯性导航系统(Inertial Navigation System,INS)。INS 是基于惯性元件(陀螺和加速度计)测量飞行器相对惯性空间的线运动和角运动参数进行载体运动信息计算的导航技术,已成为现代军用飞机、民航飞机航电系统的重要组成部分。以惯性器件为中心的导航系统是机上不可或缺的装置,是支持飞机安全飞行、引导和进近,顺利实施飞行任务的重要保证。惯性在军民两方面都有极大的需求,世界各大国历来重视发展惯性技术,惯性技术已成为国防现代化中的一项关键技术[4]。捷联惯导系统(Strapdown Inertial Navigation System,SINS)以其体积小、成本低、可靠性高等诸多优点,已在大部分场合取代了平台式惯导系统[5],在军民用航空领域均得到了广泛应用。然而由于机载SINS 直接固连在飞机机体上,飞机所处的恶劣动力学环境往往会导致系统内部参数发生变化[6]。随着SINS工作时间增加,系统的导航精度将逐渐下降[7],需要对单独的SINS进行改进。芈小龙等[8]提出了两个惯导系统的融合方案,单个惯导系统以对方输出的经纬度信息作为测量信息进行卡尔曼滤波,但对具体的融合算法并没有明显改进。谢建东等[5]对无人直升机导航系统进行了分析、设计和仿真,利用全球定位系统(Global Positioning System,GPS)导航和SINS 组成SINS/GPS组合导航系统,SINS/GPS组合导航系统可提供高精度的导航信息。李俊杰等[6]对GPS 和INS 中关键算法进行了研究。赵俊波等[7]对计程仪/INS组合方法进行了总结。Qin 等[8]通过改善GPS 环路,提高了INS/GPS系统精度,但GPS抗干扰能力差,该方法对GPS 仪器精度要求较高,难以应用。为保证导航系统的可靠性与冗余度,本文提出由三套INS 融合的配套方案,旨在提高导航精度与可靠性。仿真结果显示,本文提出的方案误差远小于单独一套惯导独自进行位置更新的误差,是开展多惯性系统信息融合的一种新思路。
2 多套惯导融合方案
2.1 多套惯性参考系统的构成
惯性参考系统主要由惯性器件模块、初始对准模块、捷联解算模块及三套惯导数据融合模块四部分组成,如图1所示。

图1 多套惯性参考系统的构成Fig.1 The composition of inertial reference system simulation module
2.2 SINS力学编排
SINS 主要由姿态矩阵解算和导航解算这两部分组成,以指北方位惯导系统力学编排为例,对核心内容的姿态微分方程、比力微分方程以及位置微分方程作简要介绍。
(1)姿态微分方程
载体b相对于参考坐标系n的姿态可以用多种数学形式来描述,常用方法有四种,即:欧拉角法、四元数法、等效旋转矢量法和方向余弦法。为表述方便此处给出基于方向余弦矩阵的姿态微分方程:



式中,vE和vN分别为载体在导航系内的东向速度和北向速度。
(2)比力方程
载体在导航系内的比力方程为:

其中
(3)位置方程

另外纬度L、经度λ和高度h的微分方程还可表示为:

上述导航方程的流程框图如图2所示。
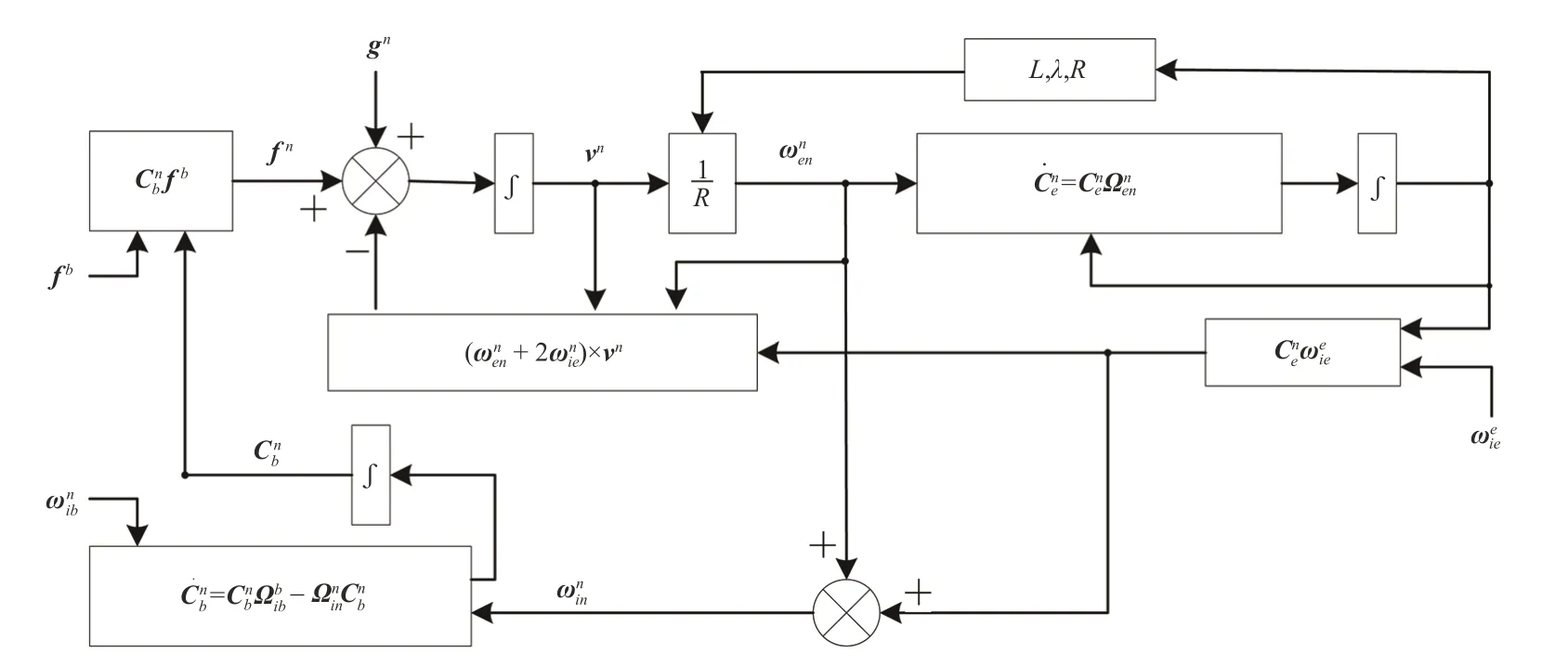
图2 指北方位捷联惯导导航方程流程图Fig.2 The flow chart of Strapdown Inertial Navigation System
2.3 基于导航结果的三套惯导最优导航解构造
在三套惯导平行安装的冗余配置方案中,三套惯导经独立解算可以得到各自的导航结果。如果不考虑导航初始误差和惯性器件的各种误差,理论上三套惯导的导航结果是相同的,三套惯导的配置只是为系统提供更高的可靠性。而在实际工程中,三套惯导由于惯性器件随机误差和导航初始误差的影响,输出的数据是不完全相同的,由此导致导航结果也不完全相同,这样会造成三套惯导输出三种不同的导航结果。而我们更希望通过对三套惯导导航数据的处理得到某种最优准则意义下最优的导航解。这样的话,三套惯导的配置可以提高整个系统的导航精度。基于此,主要研究三套惯导平行安装冗余配置条件下最优导航解的求解方法。
构造最优导航解将最优估计计算提升到导航结果层面上,而不必考虑各惯导的原始测量信号,这种方案操作简单,其优化方案的算法结构如图3所示。
在导航结果层面上做最优估计,一般只需要得到优化的位置解算结果。由于惯导系统的高度解算结果精度较低,因此这种优化处理只在纬度和经度结果上进行。因此,这种处理方法相当于将三套惯导视为位置测量传感器,在真实位置未知的情况下对位置测量的结果做最优处理。

图3 基于导航结果的最优融合算法结构Fig.3 Optimal fusion algorithm structure based on the navigation results
以纬度输出为例,设k时刻飞机的真实位置为L(k),各惯组惯导解算得到的纬度输出分别为,其中k为某一取定时间。记导航解算误差分别为δL1(k)、δL2(k)、δL3(k)。考虑各惯组的导航误差,真实位置和解算位置有以下关系成立。
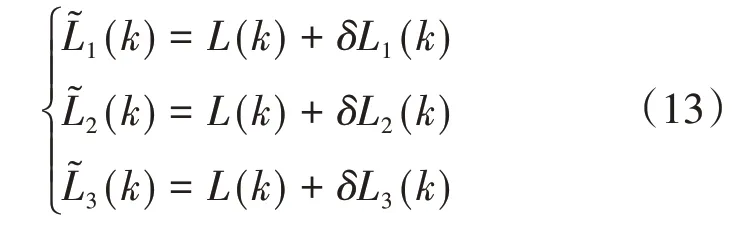
整理成向量和矩阵形式有

因此,三套惯组的解算结果在这里等价为对位置的三次有误差量测,在量测误差不可知的情况下,利用最小二乘方法可以得到真实位置的估计结果。
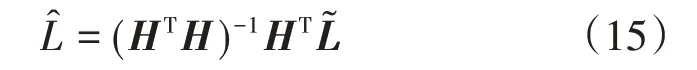
整理可得
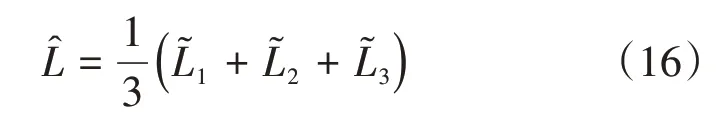
在量测噪声的方差可知或者可近似求取的情况下,可以采用加权最小二乘估计的方法求取真实位置的优化估计结果。设k时刻三套惯导的纬度解算误差的方差分别为σ2L1(k),σ2L2(k),σ2L3(k),则利用马尔可夫加权最小二乘估计的方法可以得到
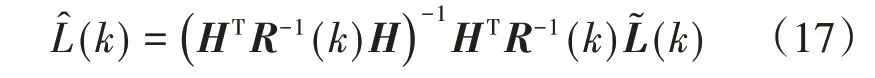
其中,R(k)为k时刻的量测噪声方差阵,有

将H和R(k)带入式可得纬度的马尔可夫估计具体表达式为
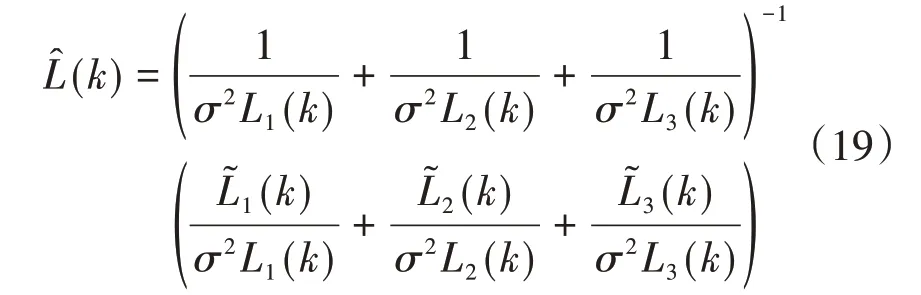
同理,经度的马尔可夫估计结果可以表示为

因此,要想通过马尔可夫最小二乘估计的方法得到当上式中L(k)和λ(k)的最优估计结果,就必须知道k时刻导航误差的方差统计特性。从产生机理分析,位置误差主要是由初始对准误差、陀螺和加速度计随机常值零偏以及随机游走引起,并且这些因素都是随机产生的。其中,加速度计和陀螺的随机常值零偏在逐次启动时随机产生,而后保持常值,成为影响初始对准精度的主要因素,进而影响到导航位置精度。总的来说,惯导的导航位置误差是随时间累积的,大致是时间t的三次函数。因此δLi(k)()i= 1,2,3 的方差是时变的,且时间越长,方差会越大。
影响位置误差的因素较多,相互间又有很大的相关性,因此,要想通过理论推导的方法得到位置误差的统计特性是较为困难的。而如果想通过统计的方法近似求取σ2Li(k),就需要大量的测试实验,对每一时刻的导航位置误差做方差分析,这种方法同样不太现实。
基于上述分析,下面给出一种对位置误差方差特性建模的方法,通过多次导航测试试验求取位置误差方差的统计模型。
位置误差的发散特性可以用时间的三次函数近似,以纬度误差为例,其均方根特性σL(k)可以描述为:
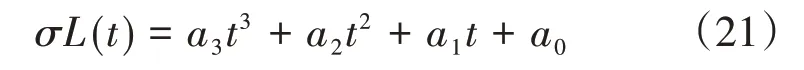
导航开始时真实纬度精确已知,因此a0= 0。这样上式可以简化为

因此只要求解出系数a1、a2、a3,就可以解算任意时刻的导航位置误差的方差特性。现在给定一套惯导IMU,在静止条件下做N次静态导航实验,为得到更好的统计结果,这里N>10,次数越多结果可信度越高。记导航初始时刻t0=0,在不同的时刻t1,t2,t3…,tk,记录N次导航解算的位置误差,仍以纬度为例,得到
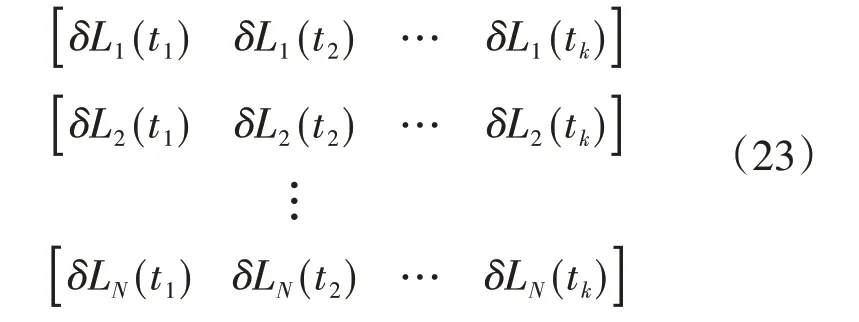
取N次导航解算的同一时刻σL(ti)导航误差,计算误差均方根特性,得到
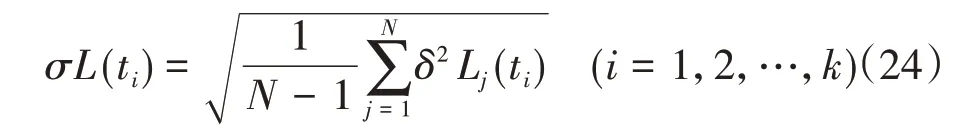
这样可以得到σL(t1),σL(t2),…σL(tk)
代入误差均方根模型,并考虑模型不准确性,整理可得

将上式记为

至此,利用最小二乘的方法可以求解出系数a1、a2、a3,具体为
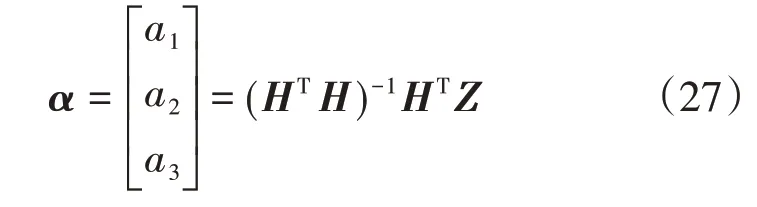
在三套惯导平行安装方案中,分别对三套惯导做上述数据处理,可以得到三套惯导导航位置误差方差特性的解析求解公式。这样,利用三套惯导的导航结果构造最优导航解就可以采用马尔可夫得到最优估计的方法,得到比一般最小二乘更加优化的导航结果。
2.4 基于历史信息的最佳混合位置求解
2.3 节介绍的对位置误差方差特性建模的方法,通过多次导航测试试验求取位置误差方差的统计模型具有较强的可操作性,但是同样需要多次导航测试试验。如果通过飞行测试试验求取位置误差的方差的统计模型,则需要耗费大量的人力、物力,对于民航客机来说并不实用。如果在实验室通过实验室静态试验建立位置误差的统计模型,虽有一定的参考价值,但是惯导系统的误差与飞行轨迹和飞行参数有很大的关系,这样建立的统计模型不能还原真实的系统误差特性。此处在2.3节的基础上利用每次飞行过程结束时刻和起始时刻飞机位置点已知的特点,通过前一次导航误差计算三套惯导的加权系数融合一个较好的位置。
由式(19)和式(20)可知三套惯导加权系数与三套惯导各自的误差方差密切相关,若对三套惯导的位置误差的方差进行归一化处理,则式(19)和(20)可变形为:
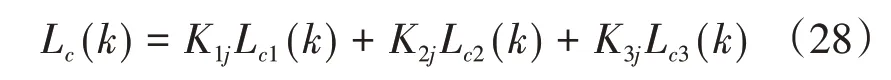
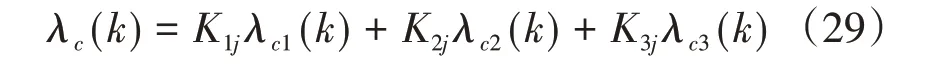
其中Lci,λci(i=1,2,3)分别为三套惯导的实时经纬度解算结果,Kij(i=1,2,3)为第i套惯导的权系数,j表示第j次飞行加权系数,可通过下式求解。

Lt:上次飞行的终点;
Ls:上次飞行的起点;
若为第一次飞行,则Ki0(i=1,2,3)取0.333。
2.5 三套惯导可用性检查及优先级实现
三套惯导平行安装的冗余配置方案中,各惯导的导航精度是有一定差异的,即便是器件参数相同的惯导,由于初始对准误差、逐次启动误差以及实时量测噪声不同的影响,各自的导航精度也会不同。在实际的导航控制过程中,往往需要从三套惯导中选取导航精度最高的一套惯导作为参考标准,这时就会涉及到导航精度排序的问题,对三套惯导的实时导航精度按照一定的评价标准进行排序,从而得到三套惯导导航精度的量化评价结果。同时三套惯导导航精度的量化评价结果也是判断三套惯导是否正常工作的条件。
2.5.1 导航精度排序方法
导航精度排序,简单的讲就是选择一个合理的导航误差范数,然后分别计算三套惯导的这一误差范数数值,按照范数数值从小到大排序的结果就是三套惯导导航精度的排序结果。通常条件下,导航误差范数一般选取导航的位置误差范数,特别是水平位置误差范数。后文的讨论都是以水平位置误差范数作为排序的参考标准,即
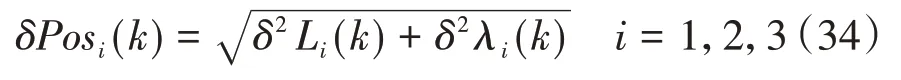
对三套惯导的导航精度进行实时排序,可以有两种方法:自主式排序方法和辅助式排序方法。其中,自主式排序方法是指不利用任何外部参考信息,而只通过三套惯导自身数据和导航结果进行排序,辅助式排序方法是指在其他导航设备辅助的情况下,对三套惯导的导航精度进行排序。
从理论上讲,要想对三套惯导的导航精度进行实时的精度排序,就必须知道飞机实时的精确导航位置信息,如果这一实时导航位置信息中没有误差或者误差量级与惯导误差相比可以忽略,那么用惯导导航位置相对于这一精确已知位置的偏离程度就可以对惯导精度进行排序。因此,这种排序方法需要引入其他导航信息,但排序方法简单易行。通常条件下,GPS 是飞机上的常用导航信息,且导航精度不随时间发散,定位精度保持在十米至几十米的水平上,可以用来对惯导的长期发散误差进行排序。如果要对几十米以下的定位误差进行排序,就需要更加精确的位置信息,这时可以考虑利用惯导和GPS 组合导航的位置信息作为评价标准。对于导航级以上的惯导设备,在与GPS 组合导航的情况下定位精度可以提高到米级水平,完全可以作为精度排序的评价标准。
在自主式排序方法中,没有位置信息的绝对参考标准,而只通过三套惯导自身的导航结果对三套惯导的导航精度排序,得到的只能是一个相对排序结果。这种情况下的精度排序更类似于一种故障检测方法或者说是一个表决机制。简单的讲,就是从三套惯导的导航结果中按照一定的优化准则提取出一组优化的导航结果作为位置参考基准,以三套惯导导航结果偏离这一参考基准的程度大小作为量化评价指标对三套惯导的导航精度进行排序。
2.5.2 自主式排序方案
自主式排序方案中没有精确的位置参考,只能利用三套惯导自身的导航结果设计评价指标,完成对三套惯导的精度排序。因此,这种自主式排序方案从原理上限制了它只能得到一个相对的排序结果,而不能得到绝对排序结果。自主式排序的过程如图4所示。
从图中可以看出,自主排序方法的关键就在参考位置的构造方法上。自主式排序方法中的参考位置直接以三套惯导的导航位置结果进行构造。这时,可以将三套惯导等价为位置测量装置,参考位置的构造就可以等价为对真实位置的最优估计,同时构造出的参考位置可以表示为三套惯导导航位置结果的加权平均形式。至此可见,参考位置的构造方法与2.3 节和2.4 节介绍优化导航解的构造方法完全相同。考虑到实际的可操作性,自主式排序方法的参考位置可以直接采用2.4节介绍的优化导航解的导航位置结果,具体设计过程详见2.4节。
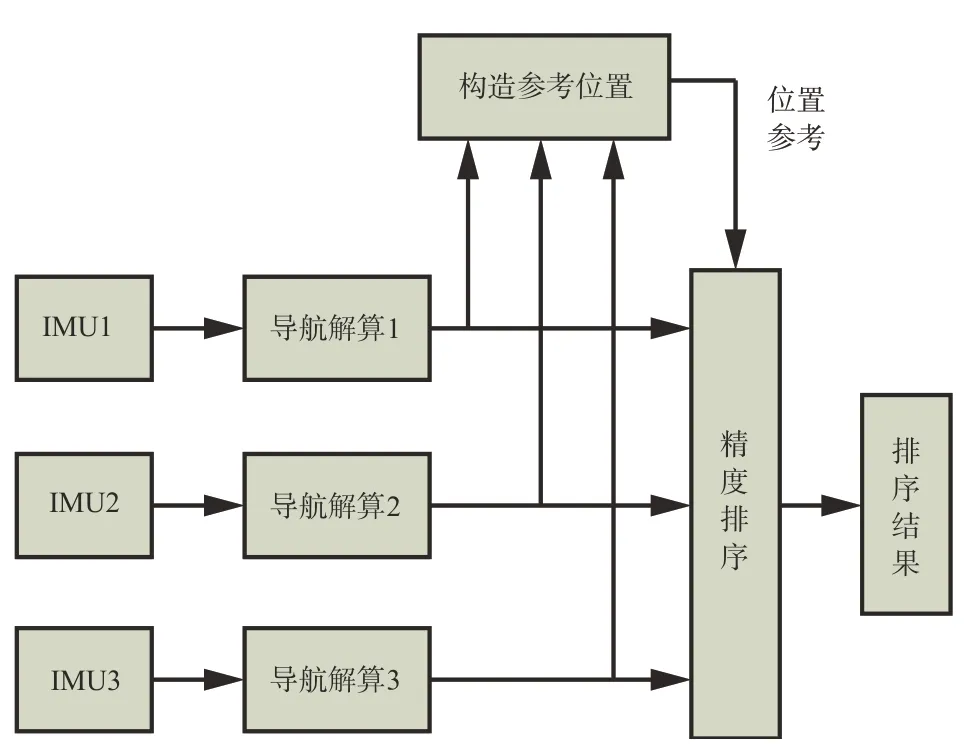
图4 自主式排序方案流程Fig.4 Autonomous sorting scheme process
设tk时刻三套惯导融合得到的混合的水平位置为Lc(k)和λc(k),三套惯导的导航水平位置结果为Lci,λci(i=1,2,3)。参照式(34),分别计算三套惯导的误差范数:

得到δPos1、δPos2和δPos3,然后对这三个误差范数排序,就可以得到三套惯导的精度排序结果。
2.5.3 可用性检查
在2.5.2 节三套惯导精度排序的基础上可以实现三套惯导的可用性检查,当某一套惯导出现故障时及时给出报警并将其隔离。具体处理算法在于通过设置误差范数的上限δPTD,当误差范数超过门限时认为存在故障。
对于航空标准惯导,当惯导同其他导航传感器断开后的定位误差满足表1所示的精度,可以参照表1设置误差范数的上限。

表1 RNP和RNA规定的组合断开后纯惯导的定位误差特性Table 1 The positioning error of inertial navigation after the combination specified by RNP and RNA is disconnected
3 导航性能分析
3.1 解算算法与载体机动误差分析
3.1.1 解算算法误差
SINS 的捷联惯导算法设计的任务主要有两个方面,一方面是要选择合适的算法,另一方面是要设计算法的更新频率和惯性器件的采样频率,而且在算法的设计中要充分考虑载体的动态性能和环境。捷联惯导算法设计的要求是,在选定惯性器件的条件下对所选的算法进行轨迹设计,算法引起的导航参数误差要小于惯性器件误差引起的导航参数误差的5%,否则应当重新进行算法设计。
在捷联惯性解算算法中,对圆锥运动和划桨运动造成的不可交换误差的补偿精度成为评价算法精度的标尺。对2.2 节所述的SINS 力学编排,对应的圆锥误差和划桨误差补偿算法如下:

上述补偿算法可根据惯性器件的采样频率、计算资源性能、导航精度要求等综合选择不同的计算子样数,其中圆锥算法漂移是制约导航算法精度的最主要因素,因此表2 给出了在10 ms 解算周期下,锥角为1°的不同锥运动频率、不同子样数下的算法漂移,据此可以选择合适的更新子样数。

表2 圆锥算法漂移比较Table 2 Cone algorithm drift comparison
3.1.2 机动对解算算法误差的影响
当前的捷联姿态更新算法是基于等效旋转矢量的多子样优化算法,其理论基础是Bortz 方程[13]。基于泰勒级数展开的多子样算法推导,将Bortz 方程经过二阶近似简化后的等效旋转矢量方程作泰勒级数展开,建立等效旋转矢量与多项式角增量之间的线性对应关系,从而求得误差补偿系数[14-15]。实际上,Bortz微分方程是一个异常复杂的非线性三维向量方程,其中包含三角函数运算,在一般角运动情况下无法精确求解,即不存在初等解。传统等效旋转矢量多子样算法都是在Bortz 方程作近似的基础上进行简化推导的,它们忽略了Bortz 方程中三阶及其以上项的影响,并将二阶项中的等效旋转矢量近似为角增量[16-17],从而才能够简化为线性微分方程。原则上,针对近似线性化后的Bortz 微分方程的求解,只有在等效旋转矢量取值比较小的情况下才能成立,越接近于0 其近似精度越高,即在低动态下效果较佳。
对于飞行速度马赫数3 以上的高超声速飞行器、或者旋转角速率高达400°/s 的高动态系统,传统的姿态求解算法误差较大无法满足需求。针对大动态下的导航解算算法可以参阅文献[16-21],对更高精度的等效旋转矢量高阶误差补偿算法有详尽的论述。针对民航客机等中低动态的载体,基于等效旋转矢量的多子样优化算法可以满足导航精度的要求,此处不再赘述机动对解算算法精度的影响。
3.2 惯性器件与载体机动误差分析
3.2.1 惯性器件误差分析
惯性器件性能是制约导航误差的最主要因素,表3列出了匀速条件下位置误差近似关系式。
总体而言,惯性器件误差造成的导航误差可以归纳为三类:一类是舒拉震荡误差,包含加速度计零位误差、初始姿态误差和初始速度误差;二类是24 h 震荡误差,包含东向陀螺漂移、天向陀螺漂移纬度误差、北向陀螺漂移纬度误差、初始航向误差和初始纬度误差;三类是经度线性漂移误差,北向陀螺漂移经度误差、天向陀螺经度误差。
粗略估算,30μg的加速度计零偏引起0~380 m的经纬度舒拉震荡误差,0.001°/h 的东向陀螺漂移引起±425 m 的经纬度地球周期震荡误差,0.001°/h的天向陀螺漂移引起0~750 m 的纬度地球周期震荡误差,0.001°/h 的北向和天向陀螺漂移24 h 内引起2 km的经度线性增长误差。
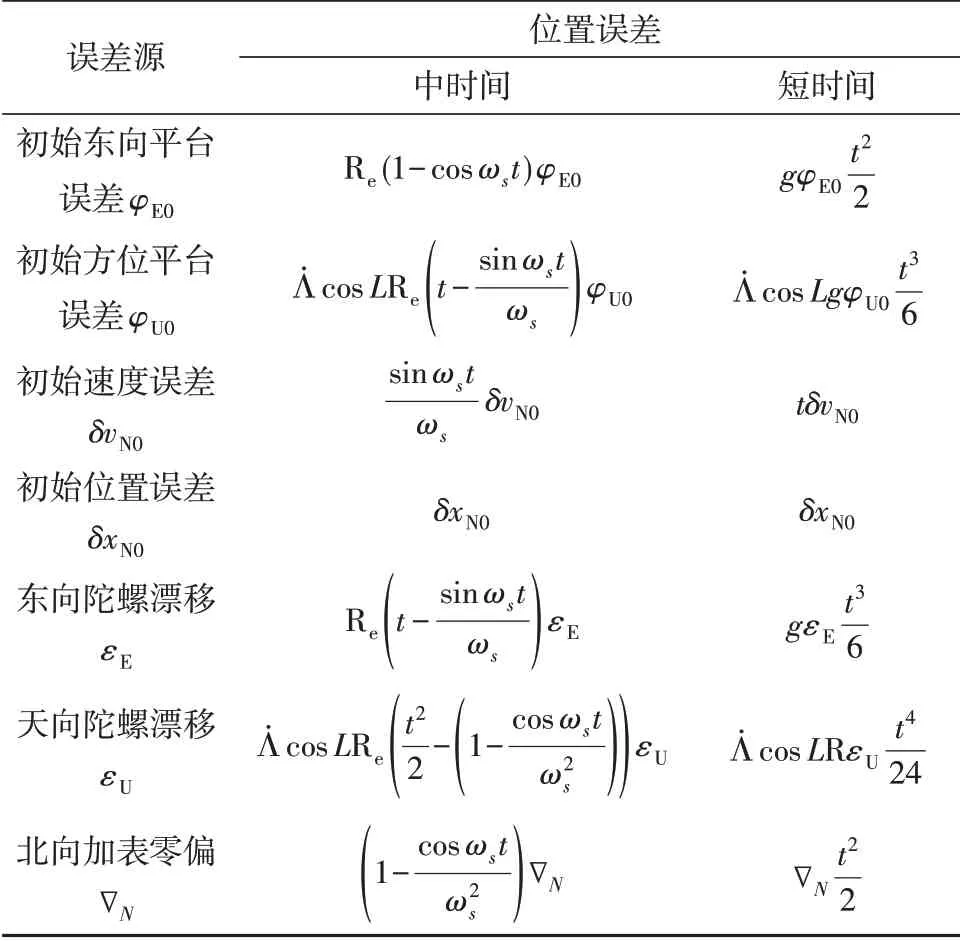
表3 惯性器件误差引起的导航位置误差Table 3 Navigation position error caused by inertial device error
3.2.2 机动对惯性器件误差的影响分析
通过3.2.1 节分析可知惯性器件的性能是影响导航性能的主要误差因素,上述分析中基于载体是静态或匀速状态,对于载体机动状态,惯性器件的动态性能亦影响导航误差。
惯性器件的动态误差主要影响因素包括陀螺和加速度计的刻度系数误差、安装误差、陀螺和加速度计的时间不同步误差、尺寸效应误差、刻度系数非线性误差、陀螺的非等弹性误差等。
对于中等精度惯性级的导航系统,制约导航性能的主要载体动态误差是惯性器件的安装误差和刻度系数误差。下面主要分析载体机动条件下,惯性器件刻度误差和安装误差对导航性能的影响。
假设载体处于平飞状态,以30°/s 的角速度做180°的横滚机动,假设存在陀螺和加速度的刻度系数误差,则机动前后导航速度误差变化率的变化值为:


粗略估计,20 min 内,1角秒的陀螺安装误差将引起60 m 的位置误差,2 角秒的加速度计安装误差将引起5 m 的位置误差,50 ppm 的加速度计刻度系数误差将引起12 m的位置误差。
3.3 多惯导融合性能分析
由(19~20)两式可知,三套惯导融合算法基于马尔可夫最优估计,理论上融合所得的位置误差是最优位置。假设三套惯导的性能一致,则融合的位置误差是单套惯导误差的 3 /3 ≈0.5574。
为验证最优性能,假设三套惯导的性能相当,均为1 nm/h的惯导,则进行50次蒙特卡洛仿真的结果如图5所示,融合的位置误差的方差为0.5678 nm/h,与理论预测值一致。

图5 三套惯导性能一致时蒙特卡洛仿真Fig.5 Monte Carlo simulation when the performance of three sets of intertial navigation is consistent
实际情况中,三套惯导的性能往往不一致,有可能性能相差加大,为验证最优性能,假设三套惯导的分别为1 nm/h、1.2 nm/h、2.4 nm/h 的惯导,则进行50次蒙特卡洛仿真的结果如图6所示,融合的位置误差的方差为0.8708 nm/h,仍比单套惯导中精度最高的性能好。

图6 三套惯导性能不一致时蒙特卡洛仿真Fig.6 Monte Carlo simulation when the performance of three sets of inertial navigation is inconsistent
4 性能仿真分析
4.1 仿真轨迹设置
仿真轨迹通过航路点设置规划相关飞行路径,其中航路点信息包括航路点编号、经度、纬度、高度、应飞速度和默认转弯方式,仿真中航路点设置见表4。从航路点设置可见,整个飞行过程包括滑跑、加速、起飞、爬升、平飞、转弯、下降、减速一系列机动动作,具体参数见图7~9。

表4 仿真航路点信息设置Table 4 Simulation waypoint information setting
4.2 捷联算法误差仿真分析
本节不考虑初始对准误差和惯性器件误差,仅考查因捷联惯导算法引起的导航参数误差。将n系下的捷联惯导姿态更新、速度更新和位置更新周期均设计为20 ms,惯性器件(陀螺和加速度计)的采样周期设计为10 ms,采用二子样圆锥和划桨补偿算法。飞行轨迹如4.1 节所述,则捷联惯导算法误差如图10所示。
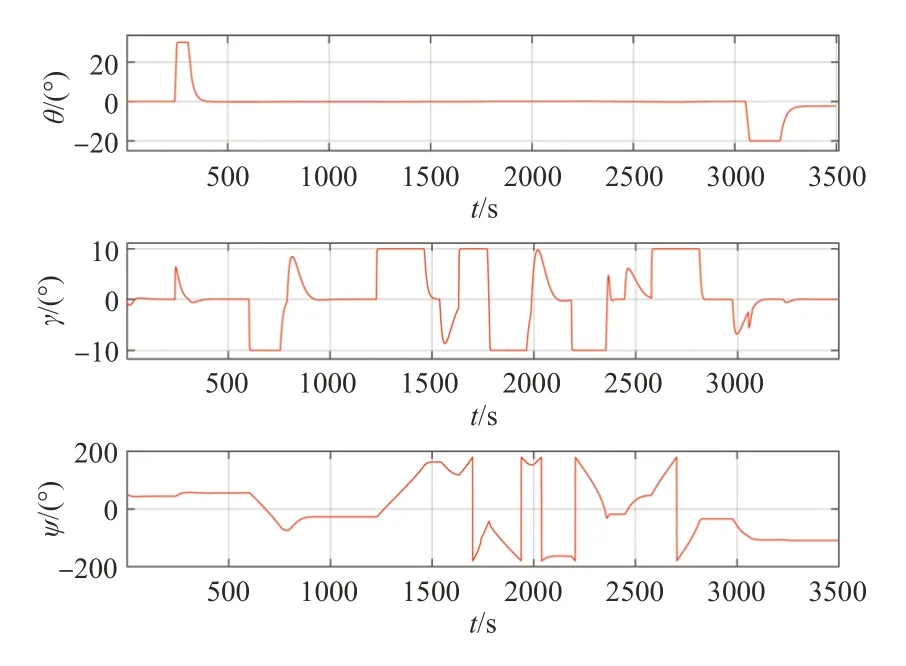
图7 仿真轨迹中的姿态信息Fig.7 Attitude information in simulation trajectory

图8 仿真轨迹中的速度信息Fig.8 Speed information in the simulation trajectory

图9 仿真的三维轨迹Fig.9 Simulated 3D trajectory
由仿真结果可以看出,载体中低速机动时带来的导航误差几乎可以忽略,采用2 子样10 ms 采样周期的更新算法,姿态误差在0.3角秒量级,水平速度误差在2×10-3m/s 量级,水平位置误差在4 m 内,符合算法误差在惯性器件误差5%的要求之内。
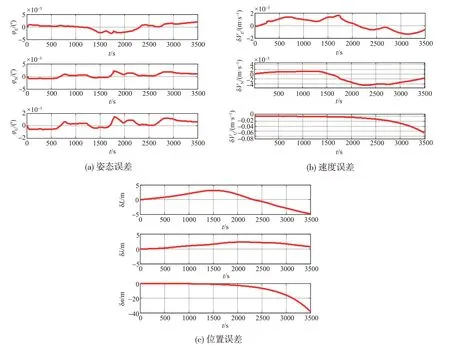
图10 捷联惯导导航误差仿真结果(仅由算法引起的误差)Fig.10 Strapdown Inertial Navigation System simulation error result(error caused only by algorithm)
4.3 惯性器件误差仿真分析
采用4.1 节的飞行轨迹,本节不考虑初始对准误差但考虑惯性器件误差,主要考查惯性器件误差存在时的导航参数误差。飞行轨迹、惯导更新周期及采样周期与4.2 节相同,惯性器件的误差参数如下所述:
陀螺常值漂移:[0.01 0.01 0.01]T(°/h);
陀螺刻度系数误差:[40 50 60]T(ppm);
加计常值偏置:[50 50 50]T(μg);
加计刻度系数误差:[50 50 50]T(ppm);
由于高度通道是发散的,当加入惯性器件误差时,发散更加严重,这时需要增加高度阻尼,这样才能保证高度通道的收敛。则惯性器件导致的导航参数误差如图11所示。
由图10 和图11所示的仿真结果知,由于高度阻尼的影响,图11 中高度通道的速度和位置比图10中无高度阻尼的结果要好的多,则高度通道的比较结果无意义。比较水平方向可知,不含惯性器件误差条件下姿态、水平速度和位置误差均比包含器件误差条件下姿态、水平速度和位置误差的5%还小,即算法引起的导航参数误差比惯性器件误差引起的导航参数误差的5%还小。因此,在大型民航客机所选惯性器件精度的条件下,所设计的捷联惯导算法能满足导航性能的要求。
4.4 三套惯导混合位置仿真分析
4.4.1 仿真轨迹及参数设置
(1)仿真轨迹
轨迹同4.1节。
(2)参数设置
三套惯组的惯性器件误差参数分别为:
IRS1:

图11 捷联惯导仿真结果(含惯性器件误差)Fig.11 Strapdown Inertial Navigation System simulation results(including inertial device errors)
陀螺常值漂移为[0.01 0.01 0.01](°/h),
加计常值偏置为[50 50 50](μg),
IRS1初始对准误差设为[-0.17′0.17′2.76′]
IRS2:
陀螺常值漂移为[-0.01 0.009-0.012](°/h),
加计常值偏置为[48-52 50](μg),
IRS2初始对准误差设为[0.18′0.17′-2.76′]
IRS3:
陀螺常值漂移为[0.009-0.013 0.01](°/h),
加计常值偏置为[-47 51-50](μg),
IRS3初始对准误差设为[-0.18′-0.16′2.48′]。
4.4.2 仿真结果
(1)IRS无故障
根据三套惯导融合算法进行仿真,仿真总时间3500 s,惯导采样周期为10 ms,更新周期20 ms,三套惯导经过位置融合后的位置误差结果如图12,仿真中高度通道引入了气压高度阻尼。
从图12看出,三套惯导根据历史信息加权融合后,最佳混合位置误差δL和δλ分别在400 m 和300 m 之内,远小于单独一套惯导独自进行位置更新的误差。
(2)IRS有故障
第一套IRS1陀螺常值漂移为[0.01 0.01 1](°/h),其余仿真轨迹及参数设置如4.4.1节所述,根据三套惯导融合算法进行仿真,仿真总时间3500 s,惯导采样周期为10 ms,更新周期20 ms,仿真中高度通道引入了气压高度阻尼。三套惯导经过位置融合后的位置误差结果如图13,三套IRS 融合有效性标志和故障惯组编号如图14所示。

图12 三套IRS融合的位置误差Fig.12 Position error of three sets of IRS fusion
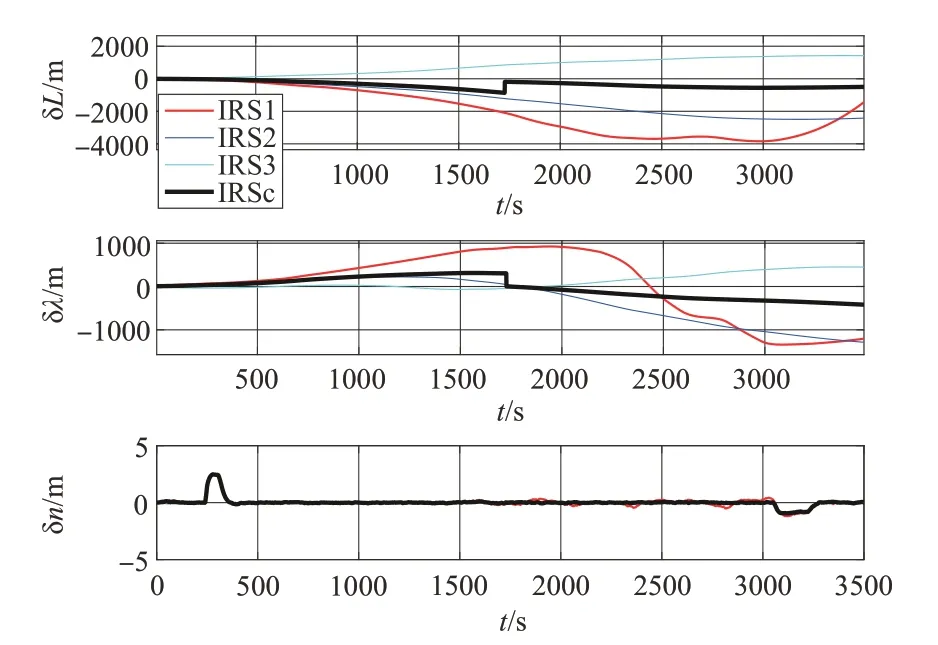
图13 有故障时三套IRS融合的位置误差Fig.13 Position error of three sets of IRS fusion when there is a failure

图14 三套IRS融合有效性标志和故障惯组编号Fig.14 Three sets of IRS fusion validity flags and failure habit numbers
从图14易看出,1800 s之前三套惯组进行数据融合,1800 s 检测出IRS1 的故障后对其隔离,IRS2与IRS3 两套惯组根据历史信息加权融合。从图13看出,对IRS1 故障隔离后,最佳混合位置误差δL和δλ分别在400 m 和500 m 之内,远小于单独一套惯导独自进行位置更新的误差。
5 结论
本文针对民航飞机飞行过程中导航精度低的问题,提出了一套多套惯导融合解决方案,继而研究了三套惯导平行安装冗余配置条件下最优导航解的求解方法。得到如下的结论:
(1)在IRS 无故障时,三套惯导可以根据历史信息加权融合后,得出最佳混合位置误差在400 m之内;
(2)在IRS 有故障时,最佳混合位置误差在500 m 之内,均远小于单独一套惯导独自进行位置更新的误差。
如上的结果可为民航客机导航提供更加精确的理论依据。
