全向移动小车编队轨迹跟踪及防碰撞控制系统研究

张晓峰，于登秀，冯 喆，徐 浩

（1.西北工业大学无人系统技术研究院，西安710072；2.西安科技大学电气与控制工程学院，西安710600）

1 引言

多智能体系统编队控制成为当前国际和国内控制问题研究领域的一个热点，其在航空航天、环境监测、社会学和生物学等领域有着非常广阔的应用前景。本文主要借助人工势场法和滑模控制方法来研究基于麦克纳姆轮的全向移动小车系统的编队控制问题。

近年来，全向移动小车引起了工业界与相关学者的广泛关注，并且在社会的各个方面得到了很好的应用［1-4］。文献［5-6］主要研究了麦克纳姆轮全向移动小车的运动学和动力学模型，解决了小车由于未知扰动和模型不确定引起的不稳定问题。文献［7］提出了一种基于模糊小波网络的非奇异终端滑模控制方法，用于麦克纳姆轮全向移动小车的轨迹跟踪和稳定，其中模糊小波网络被用来逼近控制器设计中的一些不确定非线性项。上述文献均是对一台全向移动小车的控制进行研究，然而，随着任务复杂度的增加，一些任务需要多台全向移动小车协同完成。

多台全向移动小车的协同控制属于多智能体系统的研究范畴，已经取得了一定的研究成果。文献［8］考虑了当系统拓扑图是有向图时的一致性问题，并且指出如果系统拓扑图包含有生成树，则该系统将会达到一致。文献［9］应用图论和矩阵理论解决了基于合作架构的一致性协议收敛问题。文献［10］研究了具有定向通信拓扑的二阶非线性多智能体系统的渐进一致性问题和有限时间一致性问题，运用滑模控制理论，提出两种新的分布式控制策略并进行仿真，证明了提出的方法有效。但是以上研究均未考虑智能体之间的防碰撞问题，该问题在多智能体系统的实际应用中至关重要。

人工势场法原理简单、实施方便，是实现多智能体系统防碰撞控制的有效解决方案之一［11-12］。人工势能场法的基本思想为：智能体在一个虚拟的人工势能场中运动，环境中的障碍物对智能体产生排斥力，从而使智能体能够远离障碍物。智能体在所受力的作用下，将会沿着势能场中势能最小的方向运动。文献［13］提出了一种使用人工势能场法和带有虚拟领导者的解决多智能体系统协作与分布式控制的框架，在该框架中，相邻智能体之间的相互作用力驱动智能体运动。文献［14］针对一类二阶非线性多智能体系统，结合人工势场法，提出了一种带避碰策略的自适应先导跟踪编队控制方法。但上文所述对多智能体系统的研究中，其研究对象一般为二阶线性/非线性控制模型，据我们所知，目前对全向移动小车编队防碰撞控制方面的研究甚少，本文的研究能够推动多台全向移动小车的实际应用，具有重要的指导意义。

本文研究内容如下：首先建立了全向移动小车控制模型；其次，通过图论建立了多智能体系统控制模型；接着，采用滑模控制方法设计了编队轨迹跟踪控制器，采用人工势场法实现了小车间的防碰撞，并对系统的稳定性进行了分析；最后，通过数值仿真证明了控制器的有效性。

2 背景知识

无向图G=(V，E)由它的顶点和它的无向边eij=(vi，vj)∈E⊂V×V所给出。注意对无向图而言，eij=(vi，vj)，eji=(vj，vi)标记的是同一条边。图G的两个定点vi、vj称为相邻的顶点或者邻居，如果满足边eij=(vi，vj)∈E，顶点vi的度vi∈V定义为与他直接相邻的顶点数目。

对于给定的无向图，其邻接矩阵A的元素aij取值为1或0，即：

顶点vi的度定义为：

图G的Laplacian 矩阵L定义为：L=D-A，其中D= diag(d1，…，dN)。

本文中，定义一个领导者的邻接权重矩阵B=diag[b1b2…bN]T，其中bi代表小车i和虚拟领导者之间的通信拓扑权重，如果小车i和虚拟领导者之间有通信，则bi＞0；否则bi= 0。

引理1：对于无向图而言，其拉普拉斯矩阵是半正定矩阵，所以L+B为正定矩阵。

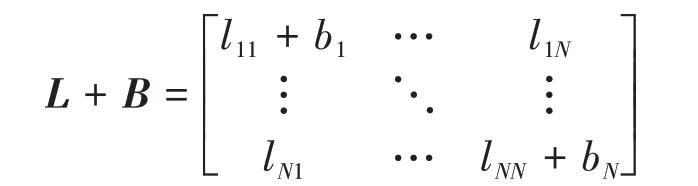
引理2［15］：函数V(t)是一个连续函数，∀t＞0，V(t) ≥0，若V˙(t) ≤-γV(t) + κ则：

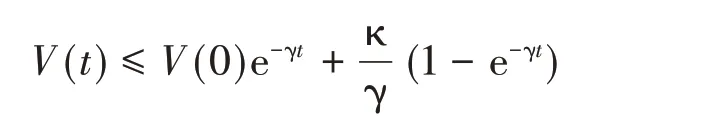
其中γ、κ为正常数。

3 编队系统描述

3.1 全向移动小车的运动学模型和动力学模型

全向移动小车框架图如图1所示，根据其结构特征以及动力学特征我们可以建立全向移动小车的的运动学及动力学模型，模型建立过程如下：

图1 全向移动小车框架图Fig.1 Frame diagram of omnidirectional mobile vehicle

VW=[VW1VW2VW3VW4]T∈R4×1为四个轮子的速度矢量，V0=[Vx Vy Vθ]T为小车自身坐标系下整体的速度矢量，R为轮子的半径，α为辊子轴线与X轴正半轴的夹角，麦克纳姆轮一般为45°。对小车进行整体的运动学分析可得系统的逆运动学模型：

系统的正运动学模型为：

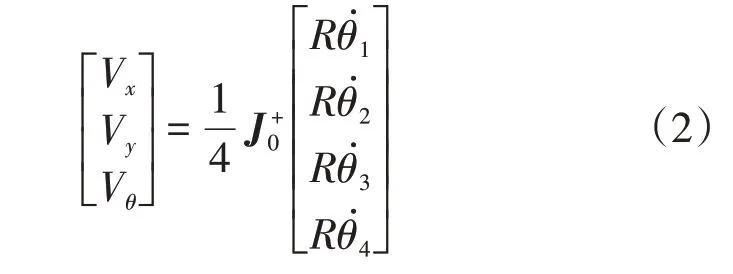
其中，

将式（2）转变为世界坐标下系统的运动学模型：

其中

世界坐标下车辆的位置和方向为x=[xw yw θ]T而J(θ)为逆运动学的雅可比矩阵，当雅可比矩阵不满秩时，系统存在运动学奇异点，此时系统失去可控性。本文取α= 45°、l1≠l2，此时雅可比矩阵满秩，因此全向移动小车通过调节各麦克纳姆轮的转速，即可改变运动状态，实现运动可控。

全向移动小车的动能方程为：

其中Vx，Vy，ωz含义同上，m是小车整体的质量，Jz是车体的转动惯量，Jω为车轮转动惯量。

考虑因为静摩擦导致的能量损失为：

其中Dθ为麦克纳姆轮的粘性摩擦系数。

引入拉格朗日函数L=T1+T2+T3-V。全向移动小车位于平面水平运动，故V= 0。

利用欧拉-拉格朗日方程：

其中τ=[τ1τ2τ3τ4]T，θ=[θ1θ2θ3θ4]T，为各轮所受的静摩擦力，并且

。

其中J+(θ)为J(θ)的逆矩阵，满足J(θ)J+(θ) =I3。

由上式可推出全向移动小车个体模型：

其中u(t) =(RJ+(θ)M-1)τ为其控制输入函数；f(t)为麦克纳姆轮型全向移动小车个体非线性动态，且

3.2 小车编队设计

以多智能体二阶一致性算法为基础，结合上述的小车动力学模型建立了一个由虚拟领导者引导的小车编队系统。采用滑模控制理论，设计了一种分布式控制器，以保证随着时间的推移，小车编队控制可以得到满足。

定义一个参考信号，使虚拟领导者沿着参考信号的轨迹运行，它的运动学模型为：

其中xl=[xlx xly xlθ]T、vl=[vlx vly vlθ]T分别表示的是参考信号的位置和速度。ul为参考信号的控制输入。

定义系统位置和速度误差为：

其中δi=[δix δiy δiθ]T代表的是小车i与虚拟领导者的相对位置向量。

并且

误差模型采用矩阵形式表示为：

取纯培养的藻液20 μL置于无菌载玻片上，用结晶紫染色固定后在光学显微镜下观察微藻形态特征。参考《中国淡水藻类-系统、分类及生态》对微藻进行初步分类鉴定。

根据公式（12），我们可以得到：

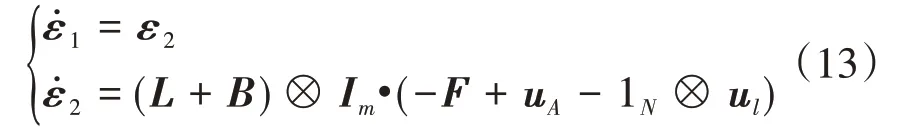
3.3 避碰问题

在系统中，全向移动小车之间，需要保持一定的间距，以保证小车之间不会发生碰撞，建立如图2所示的避碰范围。

图2 避碰范围Fig.2 The range of collision avoidance

在小车运动过程中，当小车间的范围小于rout时，它们之间可能会存在碰撞，它们之间的距离小于rin，则认为小车间已经发生碰撞。所以对于每个小车在碰撞邻域内都有一组碰撞邻居Nli=。

其中k为势能函数系数，并且

其中∇xi为xi的梯度。

4 控制器设计及稳定性证明

控制输入设计的目的是为了使小车编队系统以固定的几何队形来实现渐进一致性，同时在运行过程中小车个体之间避免碰撞。

根据滑模控制理论，为了使小车编队实现渐进一致性，我们设计整体编队的滑模流形为：

其中，μ为一正定值。

设计编队轨迹跟随控制器为：

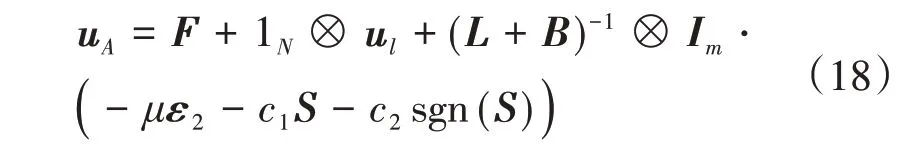
其中，c1、c2为正定值。

设计碰撞避免项的控制器为：

其中uC，j是第i个全向移动小车的碰撞避免控制项，且。

故系统总控制器u为：

定理1.对于公式（17）所示的误差系统，分布式控制器（20）能够保证集群系统跟踪误差的渐近收敛，即集群系统能够实现预期的编队轨迹跟踪及防碰撞控制效果。

证明.设计李雅普诺夫函数：

对函数V进行求导：

将总的控制输入u代入可得：

根据牛顿第三运动定律，任何两个小车之间所受的虚拟避碰斥力大小相等方向相反。对于无向图而言，拉普拉斯矩阵是对称的，所以有(L+B)⊗ImuC= 0。因此：

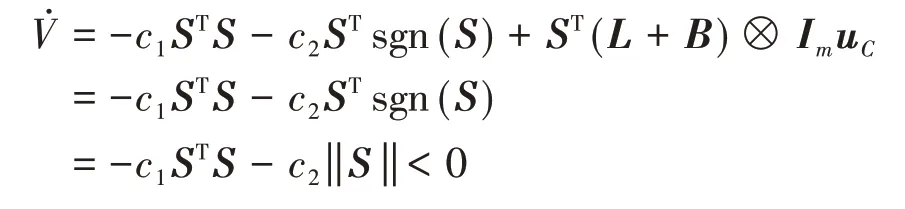
由此可得系统最终可以达到稳定状态。

当达到滑模面上，即S= 0 时，με1+ε2= 0，故：。

设计李雅普诺夫函数为：

对其进行求导得：

由引理2 可得：当t→∞时，ε1→0 同时ε2→0。

注1.文中uA能够驱动多麦克纳姆轮车系统实现预期的编队轨迹跟踪控制效果，uC能够保证系统中的麦克纳姆轮车之间不会发生碰撞，并且该部分控制输入仅在任意两台麦克纳姆轮车之间的距离时起作用。

5 仿真实验

为了验证所提出控制策略的有效性，我们进行了仿真实验。在实验中，小车编队共有六个小车。他们的通信拓扑结构如图3所示，并且在表1 中列出小车个体的主要参数值。

图3 小车编队拓扑图Fig.3 Topology of vehicles formation

表1 小车的主要参数Table 1 The main parameters of the vehicles

此外给定六个小车的初始位置分别为：x1，0=［0，0，0］T，x2，0=［-5，-5，0］T，x3，0=［5，-5，0］T，x4，0=［0，-10，0］T，x5，0=［-10，-10，0］T，x6，0=［10，-10，0］T；小车在初始位置保持静止。给定参考信号的信息为：xl=[5cos(0.1πt)，5sin(0.1πt)，0]T，分别设定每个小车与虚拟领导者之间的位置偏差向量为δ1，0=[0，0，0]T，δ2，0=[-6，-6，0]T，δ3，0=[6，-6，0]T，δ4，0=[0，-12，0]T，δ5，0=［-12，-12，0］T，δ6，0=[12，-12，0]T。

设置滑模控制参数为c1= 5；c2= 1；μ= 2，设置防碰撞控制参数为rin= 2；rout= 5。

以x方向上的编队状态为例，图4 为小车编队的位置跟踪轨迹，图5 为小车编队的位置跟踪误差，图6为小车编队的速度跟踪轨迹，图7为小车编队的速度跟踪误差。由图5 可以看出小车编队过程中可以相互之间保持固定的队形。由图4 可以看出编队中的每一个小车都可以追踪参考信号，按照参考信号的轨迹运行。由图6和图7可以看出在编队运行过程中，小车编队可以按照同一速度运行。由图8所示，两辆小车之间的最小距离在编队运动开始的阶段进入到防碰撞控制区域，但在人工势场以及编队控制算法的共同作用下迅速脱离，并且任意辆小车之间的最小距离始终与rin保持一定的偏差，说明在编队控制过程中并没有发生碰撞。

图4 小车编队在x方向的位置跟踪轨迹Fig.4 Position tracking trajectory of vehicles formation in x direction

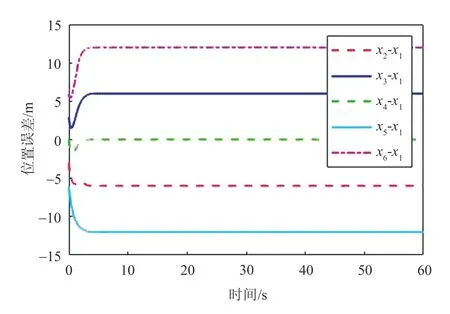
图5 小车编队在x方向的位置跟踪误差Fig.5 Position tracking errors of vehicles formation in x direction

图6 小车编队在x方向的速度跟踪轨迹Fig.6 Velocity tracking trajectory of vehicles formation in x direction

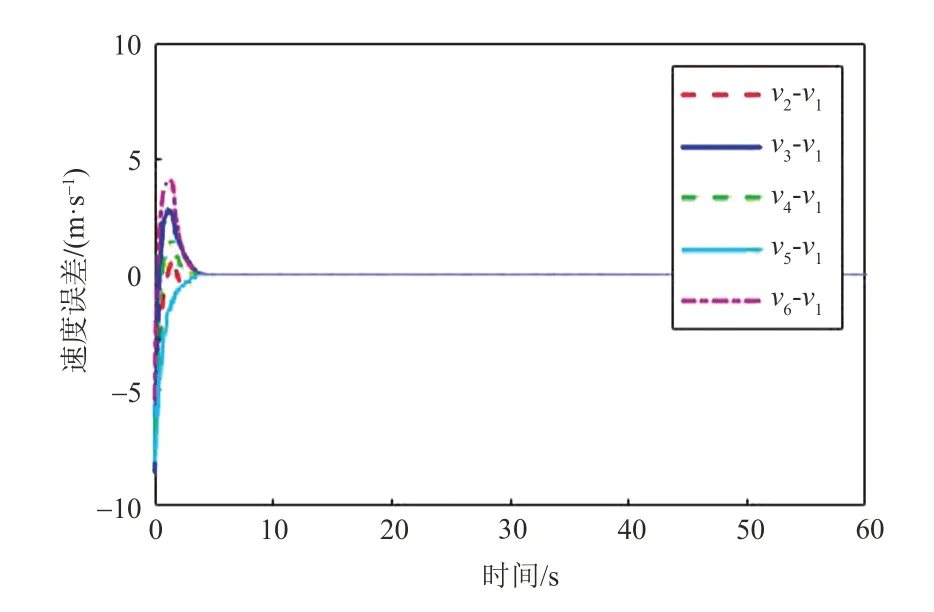
图7 小车编队在x方向的速度跟踪误差Fig.7 Velocity tracking errors of vehicles formation in x direction

图8 小车之间的最小距离Fig.8 Minimum distance between of vehicles

6 结论

本文针对全向移动小车编队的轨迹跟踪及防碰撞问题，采用滑模控制理论设计了一种分布式控制器，使小车编队以固定的几何队形逐渐到达期望的位置，并且设计了一种人工势能函数。在编队运行过程中使小车保持距离避免相互碰撞，本研究以全向移动小车为研究对象，解决了编队轨迹跟踪过程中的防碰撞控制问题，有助于加快多智能体系统的实用化进程。