柔性机器鱼的动力学建模及其游动性能分析

崔 祚, 姜洪州, 刘圣陶

(1.贵州理工学院航空航天工程学院， 贵阳 550003； 2.哈尔滨工业大学机电工程学院， 哈尔滨 150001； 3.北京遥测技术研究所， 北京 100094)

为了攫取食饵、逃避敌害和繁殖后代等生存需要，鱼类利用身体和尾鳍的往复摆动，获得远超过任何航行器的游动性能，如快速的巡游速度、高机动性和高效率等[1]。目前，仿生学研究表明，鱼类快速高效的游动性能与其外形尺寸、鱼体机械特性以及流体环境等因素存在着非常复杂的关系[2-4]。生物学研究发现当鱼体尾鳍的摆动频率与其身体的固有频率相接近时，鱼类能够获得较好的游动性能[4-5]。而鱼体本身的固有频率是由其骨骼、肌肉以及皮肤等黏弹性生物组织来决定的。受此启发，从仿生学的角度出发，在考虑流体环境影响的前提下，分析鱼体动力学参数与游动性能之间的关系，为后续机器鱼设计提供理论参考。

目前，鱼类仿生学建模主要包括动力学建模和流固耦合建模两类。流固耦合建模主要依赖计算流体力学方法，通过数值计算鱼体与流体间相互作用力，分析鱼类的游动机理。由于鱼体外形复杂且边界运动幅度较大，该建模需要消耗大量计算资源，难度较大，这方面研究大多未考虑鱼体的阻抗特性。在考虑机械谐振在鱼类游动影响的前提下，通过动力学建模，侧重研究鱼体阻抗特性与游动性能之间关系。这些研究结论将向机器鱼设计者充分展示鱼体阻抗特性对游动性能影响的重要性。

1 柔性机器鱼的动力学模型

在柔性机器鱼动力学建模中，不仅需要考虑鱼体本身的机械特性，还需考虑周围流体环境的影响。例如，Tytell等[6]发现七鳃鳗游动过程中产生最大加速度和最大稳态速度所对应的身体刚度是不同的。在动力学建模方面，McMillen等[7]利用杆理论和Taylor抗力理论，建立了柔性鱼体的离散动力学模型。Kohannim等[8]通过建立两关节离散鱼体模型，分析了鱼体刚度与其游动性能之间的关系。

自然界中鱼类通过其颉抗肌群产生弯曲力矩，并由肌腱驱动各尾椎单元体发生微小的相对旋转，整体表现为鱼体波曲线，如图1所示。目前，鱼体动力学模型主要有多体动力学模型和黏弹性梁模型两类。在多体动力学模型中，鱼体简化为多刚体串联结构，该模型未考虑鱼体的阻抗特性，适合鱼类运动学分析。将鱼体看作浸入变截面黏弹性梁，采用黏弹性梁模型进行动力学分析，利用梁理论分析弯曲变形，对应动力学方程为高阶偏微分方程[9]。但由于鱼体横截面、鱼体阻抗分布等非线性因素，理论上很难分析动力学特性。

图1 柔性机器鱼的动力学模型示意图Fig.1 Schematic drawing of dynamic model of robotic fish

Daou等[10]通过指数函数描述鱼体外形，通过求解偏微分方程得到了鱼体波近似解。Nguyen等[11]在忽略鱼体外形变化情况下，利用格林函数得到了鱼体波理论解。在上述动力学分析中，鱼体刚度和阻尼均假定为常数，缺少对游动性能影响的分析。鉴于此，将鱼类的生理结构进行简化，肌群的驱动力被简化为分布在鱼体前端的集中力矩，而鱼体的黏弹性机械特性则由脊椎的阻抗进行描述[12]。在此基础上侧重研究鱼体阻抗对游动性能的影响。

根据上述动力学模型，对其进行受力分析，如图2所示。当不计剪切应力及截面扭转时，采用伯努利-欧拉梁方法对其分析，对应的控制方程为

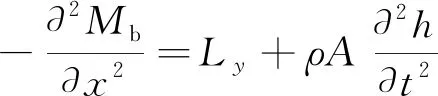
(1)

Ly为鱼体微段的水动力；Mb为驱动力矩经过黏弹性材料变形后 作用在截面上的弯曲力矩；S为剪切力；Q为截面所受的张力； h(x,t)为鱼体中心线的侧向位移，即鱼体波曲线图2 鱼体脊椎弯曲变形的受力分析Fig.2 The dynamic analysis of fish’s bending spine

由于鱼类游动的流体雷诺数较高(104～106)，故鱼体与流体间的相互作用力表现为惯性力。根据Lighthill大摆幅细长体理论[13]，鱼体推力是由向后传播的鱼体波运动所对应周围流体的附加动量所产生的，即作用于单位长度鱼体上的侧向力等于单位长度内流体虚质量所对应的虚动量对时间的导数，对应的表达式为

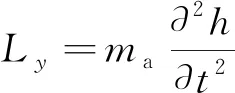
(2)

式(2)中：ma为虚质量。综合上述分析，将式(1)化解，得

(3)

求解机器鱼的固有频率时，驱动力矩为0，当鱼体脊椎的弹性EI和阻尼μI为常数，设μI=η(EI)，η为黏弹性系数。根据式(3)的形式，利用分离变量法进行求解，设解的形式为φ(x)q(t)，对时间偏导项q(t)的表达式eiλt，则幅值项可化解为

(4)

结合自由端-自由端边界条件，求解得到机器鱼的固有频率为

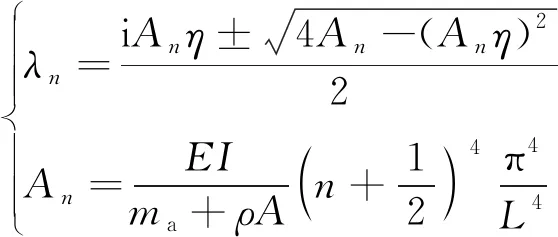
(5)

式(5)中：L为鱼体长度。

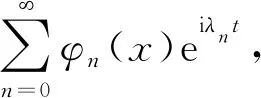
n=1,2,3,…

(6)

2 游动性能分析

仿生学研究虽然表明鱼体机械特性对其游动特性有很大的影响[7-8]，如Tytell等[5]研究发现刚度较大的鲹科或鲔科鱼类，当固有频率和尾鳍摆动频率接近时，“谐振”会对游动性能产生非常重要的影响。但是，在“谐振”状态下，动力学参数与其游动性能的关系方面的研究较少。

根据Lighthill的细长体理论[13]及其修正理论[14]，在充分考虑了鱼体尾鳍攻角影响的前提下，机器鱼平均推力T的表达式为

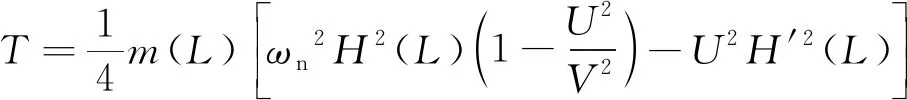
(7)

式(7)中：m(L)为尾鳍处的有效质量；ωn为固有频率；H(L)为鱼体尾鳍的最大摆幅；U为鱼体稳态游动速度；V为鱼体波波速，V=2π/λ，其中λ为鱼体波波长。

(8)

式(8)中：CD为阻力系数。

根据Lighthill的细长体理论[13]，当机器鱼的固有频率为ωn时，游动效率的表达式为

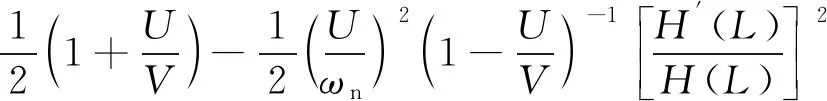
(9)

在上述分析中，机器鱼游动性能的评价除了鱼体的固有频率，还需要鱼体末端的运动学参数。

3 生物学实例研究

为研究柔性机器鱼的动力学参数与游动性能之间的关系，以鳕鱼(saithe)为研究对象[15-16]，根据其生物学参数(表1)建立鱼体动力学模型，并求解其固有频率。然后在该频率下驱动，得到鱼体波参数，并以此分析其游动性能的变化情况。

表1 鳕鱼游动的运动学参数

3.1 游动频率的分析

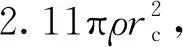
由式(6)可知，鱼体的固有频率是由其身体本身和周围流体共同决定的。结合生物学研究，可进一步预测自然界鱼类本身的共振频率可以通过肌肉组织来调节，而由流体环境引起共振频率的变化可由鱼体的阻抗特性和尾体参与摆动的长度来实现。

3.2 游动速度的分析

根据文献[15-16], 鳕鱼的鱼体波幅值分布[14]曲线如图3所示，是通过傅里叶级数进行描述。经拟合，鱼体波曲线幅值函数可写为

H(x)=0.163x2-0.084x+0.021

(10)

计算尾鳍的最大摆幅H(L)=0.10L，最大摆幅导数H′(L)=0.24L。根据式(8)，计算鳕鱼游动速度为0.90L/s，与生物学参数(0.86L/s)相接近。其原因在于在计算速度时使用的尾鳍最大摆幅为0.10L，而实验观测给出的数值为0.08L。当尾鳍的最大摆幅越大，对应的稳态游动速度越大。

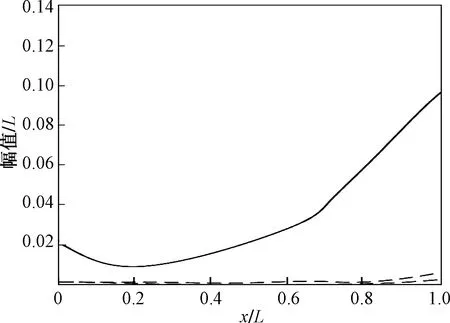
图3 鳕鱼鱼体波幅值的分布Fig.3 Lateral deflection of swimming saithe

当利用式(8)计算游动速度时，鱼体波的波速无法确定，但滑移率(鱼体波波速与游动速度之比)小于1。故先假定鱼体波波速保持不变，成比例地改变机器鱼的阻抗，然后根据式(6)求解其最优频率，分析其在最优频率下驱动的游动速度[由式(8)计算]，并与实验观测值相比较，结果如图4所示。

在图4(a)中，鱼体游动速度与其摆动频率成正比，且和尾体的摆幅以及鱼体长度直接相关，该结论与生物观测得到的结论[19-20]一致。驱动频率的变化范围较小，与生物学数据之间的关系并不明显，主要在于原文献摆动频率均在3.6 Hz左右。通过平均的方法来分析该问题，发现该区域内观测得到的数据较为密集，与模型预测的数据相吻合。

根据动力学分析，柔性鱼体可通过增加刚度来获取较高的游动速度。原因在于鱼体增加刚度以提高其共振频率来获得所需的游动速度，该结论与生物学观测[21-22]相一致。根据动力学模型分析，游动速度与鱼体阻抗的平方根呈线性变化。在图4(b)中，由于鱼体阻抗的变化范围较小，游动速度与鱼体阻抗的变化规律不明显。

在图4(c)和图4(d)中，鱼体游动速度(以每个周期游动鱼体长度的倍数BL/T表示)与其滑移率成正比，与斯特鲁哈数(St)成反比，且与大部分实验数据相吻合。同时发现，当滑移率越接近1，鱼体的游动速度越大。在鱼类游动中，St常用于描述尾迹的涡街结构，其数值范围为0.25～0.35。在该区域范围内，通常认为鱼体游动效率较高。

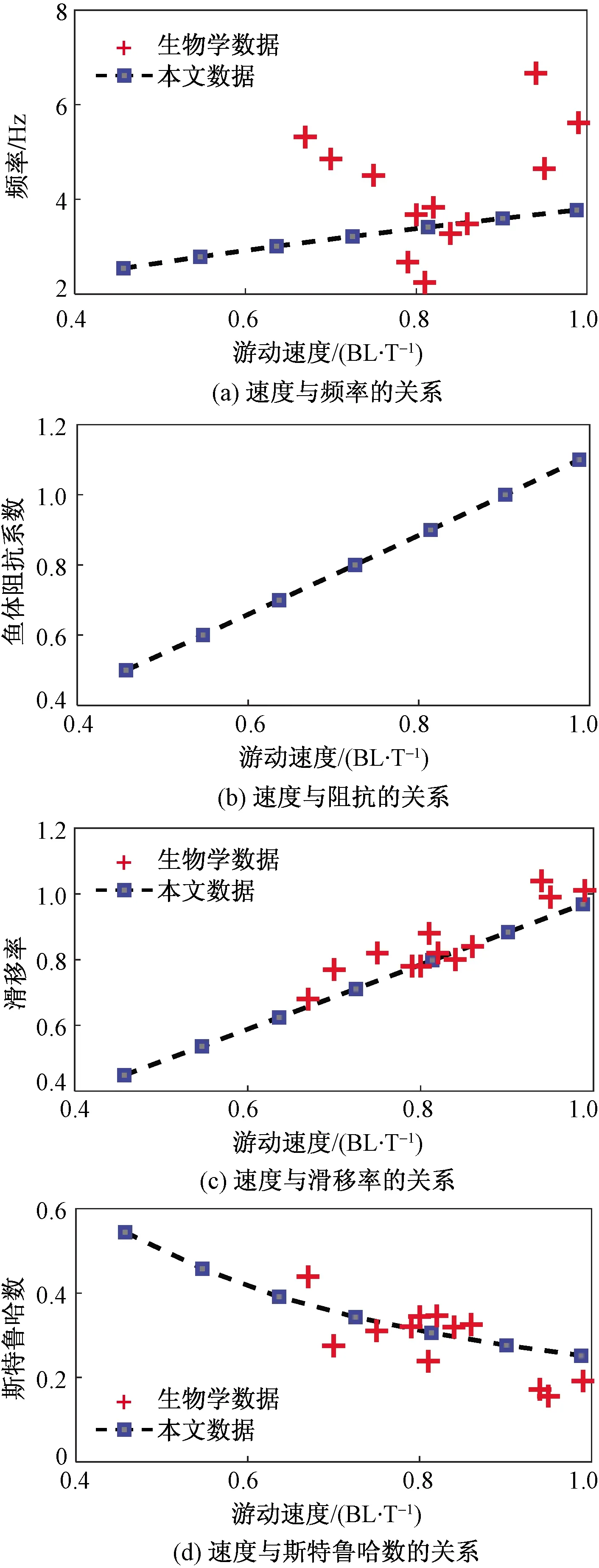
图4 当鱼体波波速不变时，鱼体游动速度与 其他参数之间的关系Fig.4 The relationships between the forward speed and other parameters with wave speed being fixed

在游动过程中，鱼体波的波速可能发生变化，但该数值低于鱼体的稳态游动速度，即滑移率须小于1。为进一步研究鱼体波波速对游动速度的影响，假设鱼体波的滑移率为常数0.87(生物学参数)，与图4分析相类似，结合动力学模型，计算鱼体波波速，并研究鱼体的游动速度与其他参数的关系，结果如图5所示。

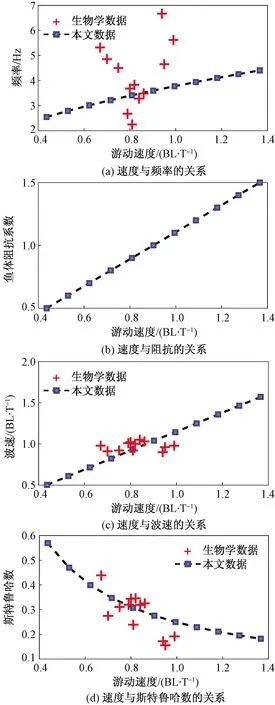
图5 当滑移率不变时，鱼体游动速度与其他参数的关系Fig.5 The relationships between the forward speed and other parameters with slip ratio being fixed

在图5中，鱼体波波速随着游动速度的增大而增大，其他参数的变化规律也与图4结论相类似。通过对比，可说明鱼体波波速也会对游动速度产生一定的影响，表明鱼体在游动过程中，滑移率可能发生变化，增大滑移率可提高其稳态游动速度。

根据动力学模型，鱼体的固有频率与参与摆动的尾体长度有关。某种意义上，尾体从左摆动到右，消耗的时间与流体流过摆动尾体长度的时间大约相等，即鱼体波滑移率可看作流体流过摆动尾体的长度与鱼体尾鳍摆动幅值之比。滑移率越大，其游动速度越大。结合对不同几何外形的鱼类游动的数值模拟，发现鱼体尾迹涡流的强度得益于鱼体前部对流体的加速过程[23]，该结论与对鱼体波滑移率的分析结果相吻合。

上述分析说明鱼体通过改变阻抗使其尾体摆动频率与其共振频率相匹配，以获得所需的游动速度。结合动力学模型，进一步预测鱼体在最优游动状态下，鱼体摆动频率和尾体的阻抗分别正比于游动速度和游动速度的平方，该结论与文献[8,18]的生物学观测结果相一致。

3.3 游动效率的分析

在游动过程中，鱼体内部肌肉组织和外部流体之间存在着能量的传递和转移。在能耗方面，总功率E为鱼体摆动传递给周围流体的机械能，该部分能量使鱼体发生弯曲摆动。在鱼体摆动过程中，设传递给周围流体的动能为K，且其反作用力对鱼体产生的功率记为TU，该部分功率表现为使鱼体向前游动的推力。从能量传递的过程来看，鱼体肌肉组织产生的功率最终分为两部分：周围流体的动能和流体反作用力对鱼体的推力功率，即E=K+TU。总的来说，由肌肉组织提供的总功率最终通过两部分进行耗散：一部分是鱼体所受阻力的耗散，另一部分是鱼类通过侧向位移将力传递给周围流体进行耗散。

当不考虑鱼体尾鳍的作用，游动效率对应的表达式为

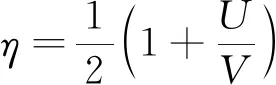
(11)

当不考虑鱼体尾鳍的影响，鱼体游动效率仅与其滑移率成正比，滑移率越大，对应的游动效率越高；当考虑尾鳍的影响时，发现尾鳍侧向位移弯曲程度越大，即攻角幅度越大，推力越小，对应的效率越低。根据动力学模型，分析得到鳕鱼的游动效率为0.423。而生物学研究[17-18]发现鳕鱼的稳态游动效率为0.52～0.72，该数值大于鱼体的动力学模型所求解的效率(0.423)。该误差与所建立的动力学模型的相关简化有关[8,24]，因为在该动力学模型中，推力主要是由鱼体的附加质量所产生。如文献[24]所述，当考虑内部肌肉传递功率以及水动力学的非线性项时，鱼体的稳态游动的效率可能大于0.5，这也说明了鱼体动力学特性对游动效率的重要影响。

4 结论

从鱼体动力学角度出发，根据Lighthill的细长体理论，建立了柔性机器鱼的动力学模型，求解了固有频率，并结合鳕鱼的生物学参数，初步探讨了鱼体在谐振状态下摆动频率、游动速度和游动效率的变化情况，得到如下结论。

(1)鱼体的固有频率是由其身体本身和周围流体共同决定的，并预测自然界鱼类本身的共振频率可以通过肌肉组织来调节，而鱼体的阻抗特性和参与摆动的尾体长度会影响由流体环境引起共振频率的变化。

(2)在最优的游动状态下，鱼体摆动频率和尾体的阻抗分别与游动速度和游动速度的平方呈正比。

(3)鱼体动力学模型对其游动效率的计算有着很大的影响。

建立的动力学模型在计算游动效率方面存在一定的局限性，但总的来说，该模型为研究鱼体动力学参数与游动性能之间的关系提供了分析思路。