位移图法计算桁架节点位移精度的讨论
2020-02-03吴晓
吴 晓
(湖南文理学院 机械工程学院,湖南 常德 415000)
1 引 言
材料力学教材[1,2]在讲授拉伸、压缩章节时,都采用法国工程师J.V.维利奥特[1]于1877年提出的位移图法求解简单平面桁架节点在外载荷作用下的位移。位移图法是一种求解简单平面桁架节点在外载荷作用下位移的近似方法,由于直观、简洁,更有利于学生在开始接触材料力学教学内容时对求解平面桁架节点在外载荷作用下位移的学习和掌握。如果不采用位移图法求解简单平面桁架节点在外载荷作用下的位移,能否用解析法求出平面桁架节点在外载荷作用下的位移,位移图法给出的位移计算结果与解析法给出的位移计算结果误差有多大,这都是值得研究的教学问题。因此,本文讨论了用位移图法求解平面桁架节点位移的计算精度问题。
2 静定桁架节点位移的求解
以图1所示三角桁架为例[2],假设各材料及横截面积均相同,AB=lACsinβ,BC=lACcosβ,研究三角桁架受力变形时A点位移AD。假设图1所示三角桁架的杆件受力皆为拉力,A点受力变形后移动到D点,其受力图可见图2。
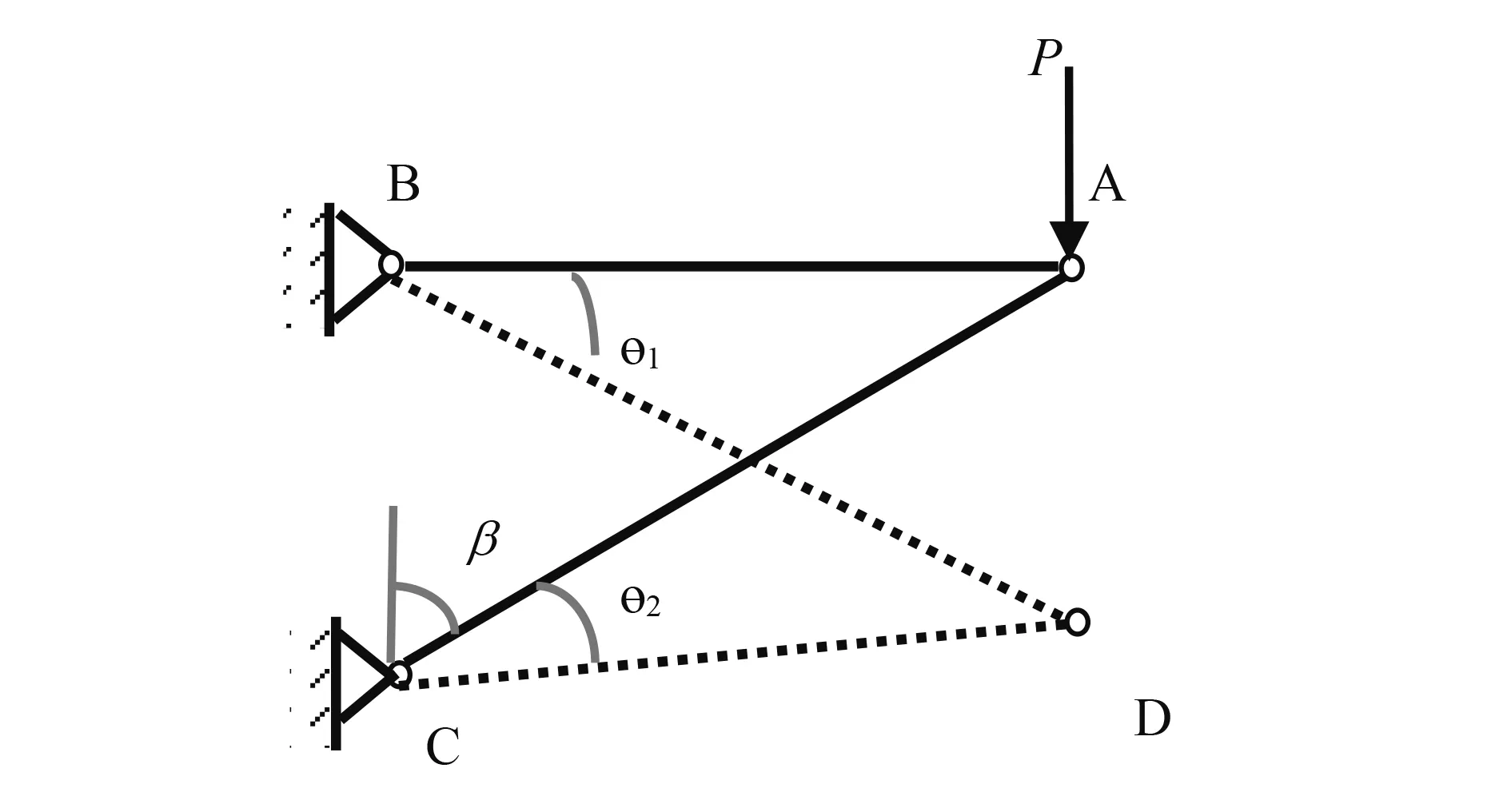
图1 集中力作用下平面三角桁架
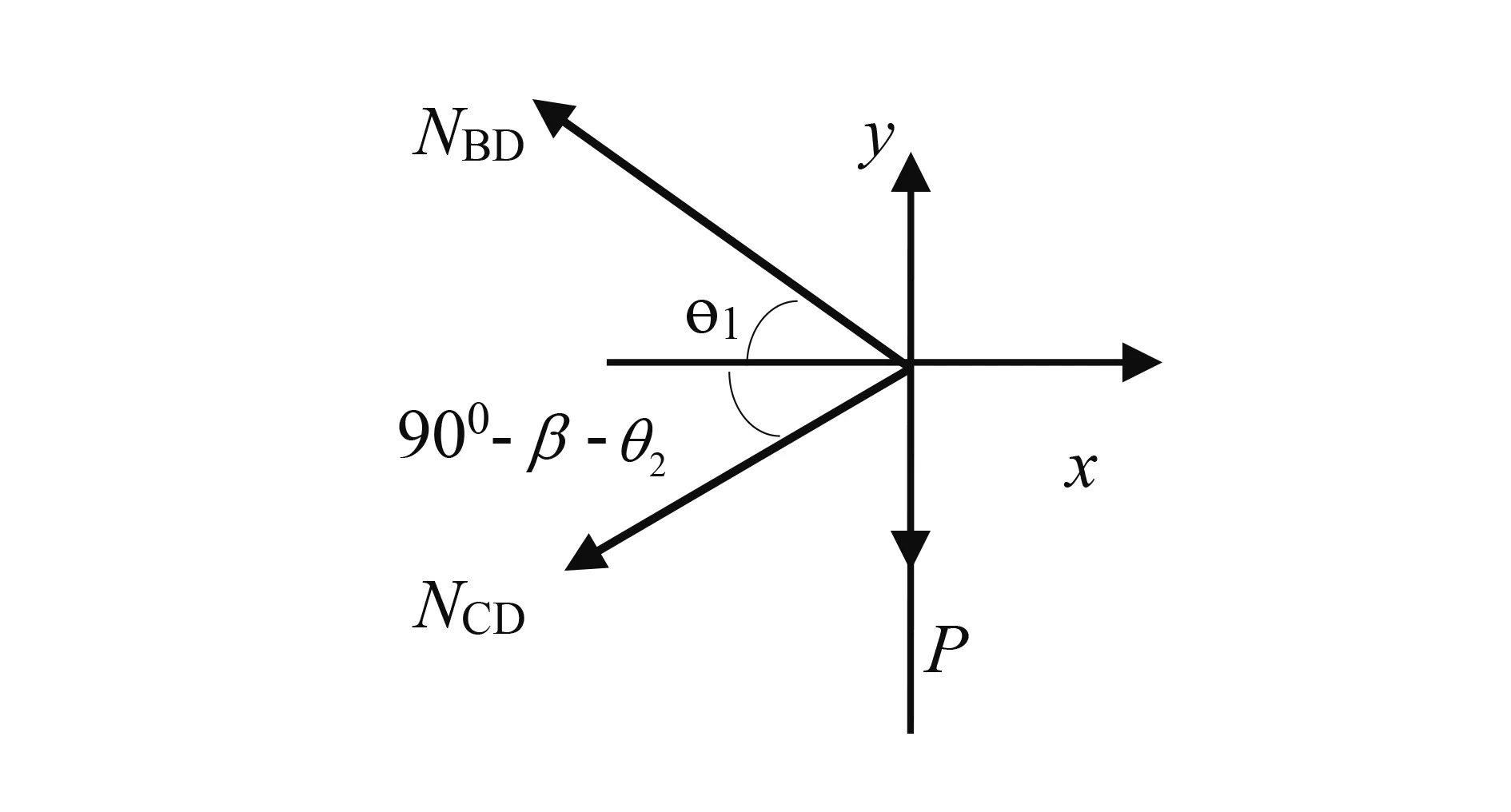
图2 节点D的受力图
由图2可列出节点D处的平衡方程为:
NBDcosθ1+NCDcos(90°-β-θ2)=0
NBDsinθ1=NCDsin(90°-β-θ2)+P
(1)
由式(1)可以求得:
(2)
由图1,利用三角函数正弦定理可得:
(3)
三角桁架变形后BD的长度为:
(4)
三角桁架变形后CD的长度为:
(5)
利用式(3)-式(5)可得:
(6)
利用式(6),可以求出θ1、θ2。再由余弦定理,可得三角桁架在集中载荷P作用下节点A变形后的位移AD为:
(7)
3 静不定桁架节点位移求解
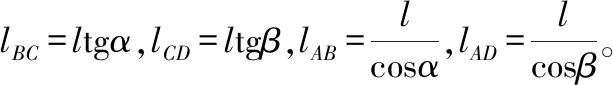
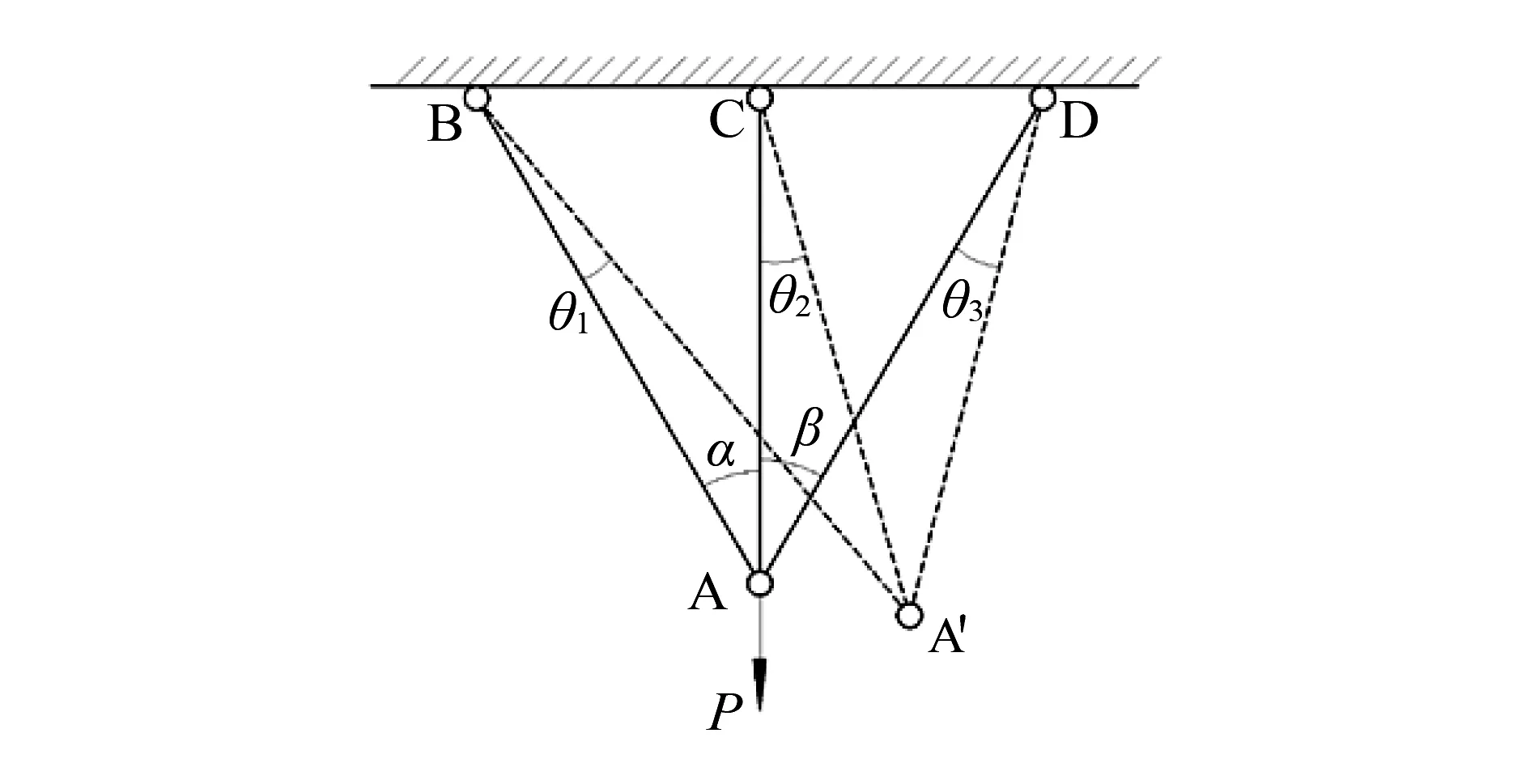
图3 静不定桁架
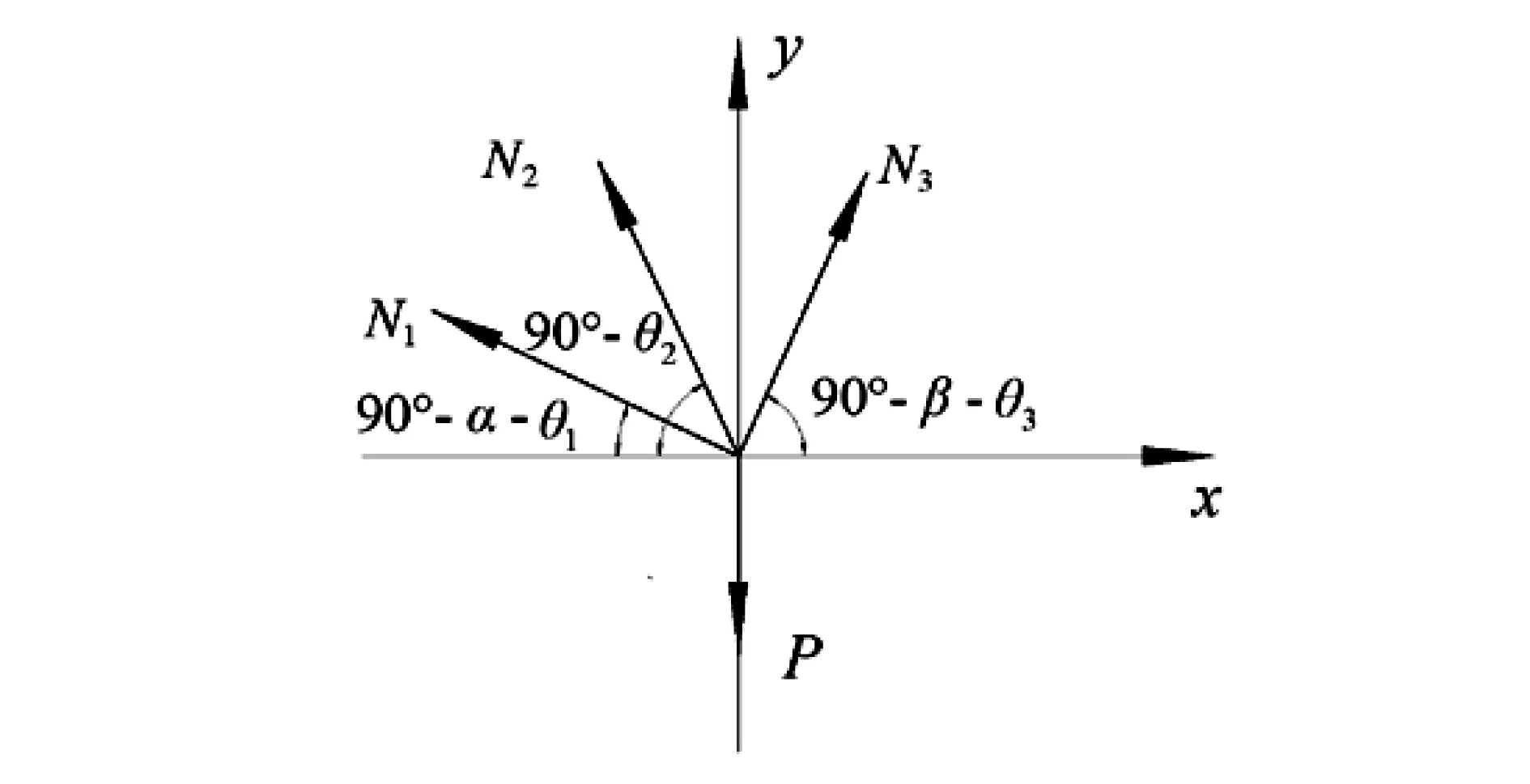
图4 节点A′的受力图
设∠ABA′=θ1,∠ACA′=θ2,∠ADA′=θ3,由图4可列出节点A′处的平衡方程为:
N1cos(90°-α-θ1)+N2cos(90°-θ2)
=N3cos(90°-β+θ3)
N1sin(90°-α-θ1)+N2sin(90°-θ2)+
N3sin(90°-β+θ3)=P
(8)
由图3利用三角函数正弦定理可得:
(9)
由式(9)可以得到:
(10)
又因各杆件在外力作用下的伸长为:
(11)
利用式(8)-式(11)可以求得:
(12)
再由余弦定理,可得静不定桁架在集中载荷P作用下节点A变形后的位移AA′为:
(13)
由式(12)求出θ1、θ2、θ3后,代入式(13)中,即可得到节点A变形后的位移AA′。
下面采用位移图法计算图3所示静不定桁架节点A的位移。文献[3]认为,桁架节点A的位移是沿着杆CA方向被拉伸,也就是默认杆CA的伸长即为桁架节点A的位移。同时,还认为杆BA、杆DA均沿各自杆长方向被拉伸,因此可知杆BA、杆CA、杆DA的拉伸长度关系为:
ΔlBA=ΔlCAcosα,ΔlDA=ΔlCAcosβ
(14)
由式(14),可得到图3所示静不定桁架的变形协调条件:
ΔlCAsin(α+β)=ΔlBAsinβ+ΔlDAsinα
(15)
式(15)与文献[3]给出的变形协调条件是一致的。再利用图3所示静不定桁架节点A的静力平衡方程并结合式(15),即可得到节点A变形后的位移为:
(16)
4 计算分析及讨论
下面通过两个简单算例讨论分析位移图法的计算精度。
算例1:
以文献[2]三角桁架为例计算节点D的位移。三角桁架相关参数为:sinβ=0.6,E=200GPa,P=60kN,AAB=3.14×10-4m2,AAC=1.02×10-3m2,AB=1.2m,AC=2m。把有关参数代入式(7),可求得θ1=0.0746°,θ2=0.0466°,节点D的位移为AD=1.785mm。而文献[2]采用位移图法求得节点D的位移为AD=1.78mm。
由以上计算可知,式(7)计算结果与文献[2]计算结果的误差仅为0.28%,这说明在三角桁架满足强度条件的前提下,此算例采用位移图法计算三角桁架节点的位移,所得计算结果是足够精确的,完全可以满足实际工程的要求。
算例2:
以文献[3]桁架为例计算节点A的位移,桁架相关参数为:E=200GPa,A=3.14×10-4m2,P=60kN,lAC=1.2m,α=45°,β=30°。把有关参数代入式(12)中,可以求得θ1=-0.0174°,θ2=-0.0046°,θ3=0.0096°,这说明桁架节点A在外力P作用下变形后的位置,在桁架节点A变形前的左边。把相关参数代入式(13)中,可求得节点A变形后的位移AA′=0.6385mm;把有关参数代入式(16)中,可得采用位移图法求得节点A的位移为AA′=0.5726mm。解析法计算的节点A位移是斜直线,位移图法计算的节点A位移是沿CA方向伸长的直线,因此解析法计算结果大于位移图法计算结果,而解析法给出的节点A的位移却是图3所示桁架的真实位移。
由算例2可知,式(13)计算结果与式(16)计算结果的误差为11.51%, 这个误差远远超过了实际工程所允许的误差5%。造成误差的原因是文献[3]对图3所示桁架节点A位移的方向做出了不合理的假设。因为,只有当α=β时,图3所示静不定桁架节点A位移才是沿CA方向伸长的;当α≠β时,图3所示静不定桁架节点A位移是在桁架节点A变形前的左边或右边的斜直线。所以,采用位移图法计算桁架的节点位移时,应根据桁架的受力实际情况对节点位移方向做出合理的假设,这样才能控制位移图法的计算精度不超过实际工程所允许的误差5%。
5 结 论
由以上算例可以看出,解析法的计算结果均大于位移图法的计算结果,其主要原因是用位移图法计算桁架节点位移时,只能对桁架节点位移的方向做出近似假设。
以上分析可以在教学中做简要分析介绍,让学生了解采用位移图法求解桁架节点位移虽然直观、简洁,但是采用位移图法求桁架节点位移有时也存在计算精度会超过实际工程所允许误差5%的不足之处。
