基于改进型Harris尺度不变特征的图像配准算法研究

郑 瑶

(梧州学院 电子与信息工程学院，广西 梧州 543002)

图像配准(Image Registration)是图像处理研究领域的一项重要内容，可以实现对2幅或多幅图像的比较或融合[1]，在图像拼接、图像识别、遥感监测与监控等计算机视觉领域应用广泛。根据图像配准中利用的图像信息的不同，可将图像配准方法分为3大类：基于灰度图像配准、基于变换域图像配准和基于特征匹配的方法[2]。其中，基于特征图像配准的方法利用了图像的显著特征(如角点、斑点和区域等)进行匹配，具有计算量小、速度快、精度高，即使图像在噪声干扰、仿射变换等情况下也具有较强的鲁棒性等优点[3]，是图像配准技术的主流方向，也是笔者重点研究并加以实践的图像配准方法。

使用特征点匹配的主要步骤如下：特征点检测、生成特征描述子、特征点匹配[4]。常用的特征点提取算子如Harris角点检测、尺度不变SIFT特征点检测、加速稳健SURF特征点检测等。其中，Harris角点检测与SIFT特征点检测性能稳定，一直是图像配准算法研究的热点。Harris角点检测算法于1988年由Harris提出[5]，通过构造1个2×2的Harris矩阵，利用微分算子和矩阵特征值进行特征点的判定，具有较高的检测率，并且不易受光照、旋转、噪声等的影响。但是，该算法不具备尺度不变性，在图像缩放后，角点定位存在偏差，导致匹配不准确。SIFT算法在2000年由Lowe提出[6]，利用金字塔和高斯滤波差分来构建高斯差分尺度空间，以使算法具备尺度不变性。此外，SIFT特征在图像旋转、仿射变换和视角变换下也有很好的不变性，对噪声的影响也表现出了较好的鲁棒性，被广泛地应用于图像配准和图像识别领域中。但是，该算法也存在缺陷[7]，由于每个特征点的检测都需要在多个尺度空间下与邻域进行比较计算，计算过程较为复杂，难以适应实时运算的需求。

由于Harris角点检测算法和SIFT特征点检测经典算法各自存在缺陷，所以本研究提出一种基于Harris尺度不变特征的图像配准算法，即在多尺度下，采用改进的Harris角点检测算法进行角点检测；对于目标像素点，再以该点为中心的3×3的8邻域内进行角点响应最大值的搜索。为了求得角点在位置空间和尺度空间的精确响应值，还需验证每个尺度下的候选角点在LOG尺度空间中是否是极值点，以实现精确定位。特征点提取后采用改进的SIFT特征描述子对特征进行描述，利用圆自身的旋转不变性，避免了主方向的确定，从而生成64维特征描述子。图像配准过程中采用欧式距离作为相似性度量，进行2幅图像特征点对的粗匹配，并使用RANSAC算法来消除误匹配点对，完成图像配准。采用MATLAB 7.0对本研究提出的算法与经典SIFT图像配准算法进行仿真试验对比，从旋转变化、角度变化、仿射变化、尺度变化等方面来验证本算法的可行性。

1 尺度不变性Harris角点检测算法

经典的Harris角点检测算法计算简单，提取的角点稳定可靠，具备旋转不变性、光照强度不变性，但是不具备尺度不变性。因此本研究在经典Harris角点检测算法中引入尺度空间[8]，将Harris角点检测算子与高斯尺度空间相结合，使Harris角点检测算法具有尺度不变性，能在多个尺度下检测特征点，并根据拉普拉斯响应极值确定特征尺度。

1.1 多尺度Harris角点校测

与经典Harris角点检测算法一样，一幅图像在不同尺度下的尺度空间L(x，y，σ)也是由图像I(x，y)与二维高斯函数g(x，y，σ)的卷积运算产生：

L(x，y，σ)=g(x，y，σ)⊗I(x，y)

(1)

其中，σ是尺度因子，本研究设高斯平滑函数的尺度参数分别为σ0、kσ0、k2σ0、k3σ0…ks-1σ0，s表示尺度空间中图像的层数，如图1所示：

图1 尺度空间搜索图

多尺度的自相关二阶矩阵M相应表示为

(2)

与经典算法相比，该矩阵增加了2个高斯尺度参数[8]，σI为积分尺度，它决定Harris角点当前尺度变量，该值越大说明尺度越大。σD为微分尺度或者局部尺度，它决定角点附近微分值变化的变量，是一个高斯平滑参数，抑制拉普拉斯变化后产生的微小噪声点。

经典Harris角点检测算法计算二阶矩阵M的行列式的值det(M)和矩阵的迹trace(M)，并根据公式(3)计算每个像素点的角点响应函数值：

R=det[μ(x,σI,σD)]-αtrace2[μ(x,σI,σD)]

(3)

公式(3)中的α凭经验取值，一般取0.04～0.06，经验值使得角点定位出现偏差，影响后续的图像配准精度。

为了避免α值的选取，本研究采用文献[9]中的方法，角点响应函数的表示为

(4)

公式(4)中，ε可以取任意小的量以防止出现分母为0的情况。

计算出角点响应值后，第一步通过人为设定阈值TH，判断某尺度σn下，角点响应值R是否满足大于阈值TH，阈值TH=0.01×Rmax，Rmax为角点响应最大值。对于满足第一步的角点作为候选角点，第二步采用8邻域内角点响应极大值搜索。

1.2 角点特征尺度值搜索

应用尺度空间后，多尺度Harris算法需要在每个尺度σn都进行检测，会检测出大量的冗余特征点，增加了运算时间。本研究采用自适应尺度选择的角点检测算法，即找到局部特征点的典型尺度，此时该特征点就无需再用原来的多个尺度来表示，将2幅图像里的特征点各自变换到典型尺度下，即进行归一化操作就可以进行匹配。这样既满足了尺度不变性，又在一定程度上去除了冗余特征点，简化计算量。典型尺度根据候选角点对应不同尺度LOG的响应程度值来计算，找出LOG响应值最大的尺度，即LOG窗口半径3σ[8]。

LOG函数计算公式为

LOG(x,σn)=σ2|Lxx(x,σn)+Lyy(x,σn)|

(5)

搜索具备典型尺度的特征点及典型尺度值可以采用精确的迭代方法，但计算复杂，本研究采用简化方法，即验证每个尺度下的候选角点在LOG尺度空间中是否是极值点即可，若不是极值点则删除该点。

上述算法引入了尺度空间，并利用尺度空间的拉普拉斯响应确定特征尺度值，从而减少了其他尺度空间冗余点的检测。在计算角点响应值时避免了对自相关矩阵M的特征分解，也避免了系数α的选取，在一定程度上保证算法的稳定性和准确度。

2 特征点描述

检测出Harris特征点后，为了实现特征点的匹配，还需要利用特征描述符来描述每一个特征点与周围图像的相互关系，生成特征向量。SIFT特征描述以特征点为中心，在以3σ为半径的邻域内划分4×4个区域，然后在每个区域内计算8个方向的梯度并构建梯度方向直方图，梯度最大的方向作为主方向，从而为每个特征点形成128维特征向量[10]，每个特征点都具备位置、尺度、方向3个信息(x，y，σ，θ)[11]。

SIFT特征描述子具备较好的尺度不变性、旋转不变性，归一化处理后也可以更好地消除光照的影响，但是128维的特征描述子使得算法计算量太大，耗时过长。因此本研究对SIFT描述符进行改进，根据文献[11]，利用圆来构造特征描述符，生成64维特征矢量。

改进的描述符构造步骤如下：

(1)以特征点为中心，构造一个半径为8的同心圆环区域，如图2所示：

图2 多尺度Harris角点特征描述符

(2)仿照SIFT特征描述符的方法，计算每个像素梯度的幅角和幅值：

(6)

(7)

(3)统计第一个圆环内像素在8个方向上的梯度累加值。由于圆本身具有旋转不变性，每一个圆环内的像素在图像旋转前后只有位置信息发生变化，而相对信息保持不变。因此，8个方向上的梯度累加值按照最大值循环移位的方式作为特征描述符的第1～8个向量。最大值循环移位法表示每次都将向量的最大元素移至向量头部，这种做法可以避免在后续特征点匹配过程中，避免减小2个向量间的欧氏距离度量值。

(4)按照上述方法统计其余圆环内的8个方向上的梯度累加值。8个同心圆环一共生成8×8=64个元素，因此本研究用64维向量作为特征点的描述符。

改进的特征描述子利用了圆自身的旋转不变性，因此不需要给特征点指定主方向。通过对每一圆环内梯度累加值的最大值循环移位，可以消除向量间欧氏距离度量减小的后果，提高后续匹配的精度。将SIFT128维特征描述矢量降低至64维特征矢量，可以减少特征描述算法的复杂度，在后续匹配过程中缩短搜索时间，提高匹配速度。

3 特征点匹配

3.1 初始匹配

本研究选取欧氏距离函数作为相似性度量进行特征点的匹配。在待配准图像中搜索与参考图像某特征点距离最近和次近的2个特征点，然后将2个距离的比值与人工选择阈值δ进行对比，本研究阈值δ选取0.5。小于该阈值的确定为初始匹配特征对。同时，为了提高初始匹配对的精度，本研究采用双向匹配策略，在2幅图像中分别得到2组匹配点集中搜索相同的匹配特征点对，保留相同的特征点对作为初始匹配对。

3.2 匹配对提纯

以上建立的初始匹配对中还可能存在着错误匹配对，本研究采用RANSAC随机抽样一致性算法[12]对变换矩阵进行估计，RANSAC算法通过反复提取，采用最小的点集计算该变换矩阵的初始解，对点集与初始解的符合程度进行检验，然后将距离小于阈值的点集作为内点，大于阈值的点集作为外点去掉，最后再利用内点重新计算变换矩阵的参数。RANSAC算法在求解的过程中剔除了误匹配点，在保证图像配准的精度和鲁棒性的同时，也使得图像配准速度大大提高。

4 试验结果及分析

为了验证本研究算法的可行性，选取4组图像进行验证，每组图像均采用经典SIFT图像配准算法以及本研究算法进行仿真，图像匹配结果见图3～6。试验平台为Windows 10操作系统，编程环境为MATLAB7.0。图3中图像为256×256的bmp图像，图像经过了角度的旋转变化；图4中图像为510×472的jpg图像，是同一个场景在不同视角下所得到的2幅图像；图5中图像为1024×720的jpg图像，图像经过了仿射变换；图6中a图尺寸为300×211，b图尺寸为341×240。b图在a图的基础上尺寸增大。每组图像的检测时间、特征点数、匹配点对数见表1。

图3 旋转变化的图像配准

图4 角度变化的图像配准

图5 仿射变化的图像配准

图6 尺度变化的图像配准

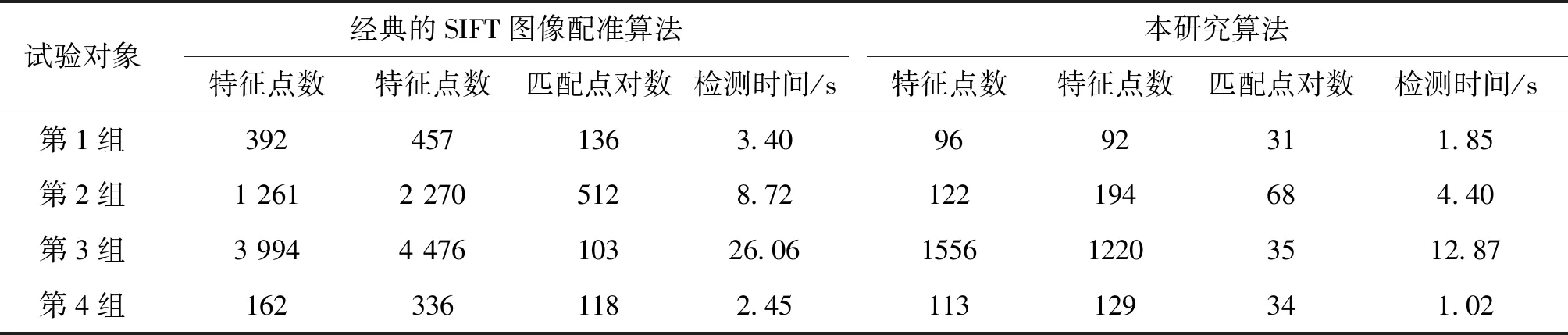
表1 旋转变换的图像配准试验结果

本研究结果表明，在多尺度下，采用改进的Hariis角点检测算法相对于经典SIFT算法具备对旋转变化、角度变化、仿射变化、尺度变化的不变性，同时还具有明显的时间优势。由于采用了自适应尺度选择的角点检测，特征点无需用多个尺度来表示，且描述子降为64维特征矢量，从检测数据上看检测时间减少了约50%。另外，通过对比本研究算法与经典SIFT算法所提特征点在图像中的分布，可以看出，本研究算法所获得的匹配点对数减少，且均匀分布在图像的主体部分，基本无错误匹配点对。因此，本研究算法具有较高的准确率。

5 小结

本研究在基于灰度的Harris角点检测算法的基础上引入尺度空间理论，采用基于尺度不变性的Harris角点检测算法对特征点进行检测。检测到的特征点除了具有旋转不变性、光照不变性、仿射不变性、尺度不变性的特点。特征点检测后，利用圆来构造特征描述符，以生成64维特征矢量，从而减少后续匹配时间。在特征点的匹配过程中，采用穷尽搜索算法对待配准的2幅图像实现双向匹配，得到的初始匹配对再使用RANSAC算法进行提纯，从而实现图像精确配准。最后，采用MATLAB 7.0对本研究提出的算法进行了仿真试验，试验证明该算法可行。该算法与同样基于尺度空间理论的SIFT算法相比，具有更高的检测速度。