面向物联网的传感器采样数据分配策略研究

高朝营

（枣庄科技职业学院 山东省枣庄市 277599）

物联网作为当前新兴的热门技术，其主要作用是将物理世界中的各个事物通过相互之间的通信协议完成规定的共同任务[1]。所有的信息系统均需要对传感器采集到的数据进行存储，从而获取传感器数据的实时值，并进一步获取根据采集到的数据信息反映的真实物理量的变化，实现对事物的智能化分析[2]。在实际生产以及生活中，海量传感器采样数据的变化趋势与某一具体数据相比具有更高的利用价值，因此通过传感器查询的操作通常是针对统计信息进行，采样数据在访问过程中经常出现失衡的现象。基于此，本文开展面向物联网的传感器采样数据分配策略研究。

1 面向物联网的传感器采样数据分配策略研究

1.1 建立物联网采样数据分配函数

针对物联网进行数据采集的传感器在对数据进行存储时，通常会采用分布式的存储方式，将物联网传感器采样数据存储在与之相邻的服务器当中。针对这一特点，本文分配策略在对传感器静态数据和动态数据进行分配前，首先要将数据分配为一个抽象的数学函数。将传感器采样数据块映射到各个存储节点当中，通过建立分配函数对其进行分析[3]。在分配函数中输入量为传感器采样数据块的集合，输出两个传感器采样数据块集合的不同划分。根据映射特点，将映射过程看作是一个转移矩阵，该转移矩阵能够将输入量按照一定要求及约束条件得到最终的映射输出量。

同时，在对传感器采样数据分配前还需要指定目标，根据需要设置不同的目标优先级，由于在物联网中传感器采集数据的过程中会受到众多因素的影响，因此根据不同的分配目标，优先级的侧重点也不同，通常情况下，影响传感器采样数据分配优先级的因素包括以下几个方面，如表1 所示。

根据上述四个影响因素，首先定义K（TR、CH、IM、ID）为分配目标的优先值函数，其数值是根据表1 中列举的各项因素经过适当的运算获得。再定义K'（TR、CH、IM、ID）为分配目标的优先级函数，其数值是目标函数在所有目标有限值当中的排序次序[4]。当给出 相应的分配目标时，则优先级最高，取K'（TR、CH、IM、ID）=1。再定义物联网采样数据分配函数的输入量为X=[x1，x2，x3，……xn]T，其中各个分量均表示为不同的数据块。定义物联网采样数据分配函数的输出量为Y=[y1，y2，y3，……yn]T其中各个分量均表示为每个物理节点具有的负载率。根据上述定义，得出物联网采样数据分配函数为：

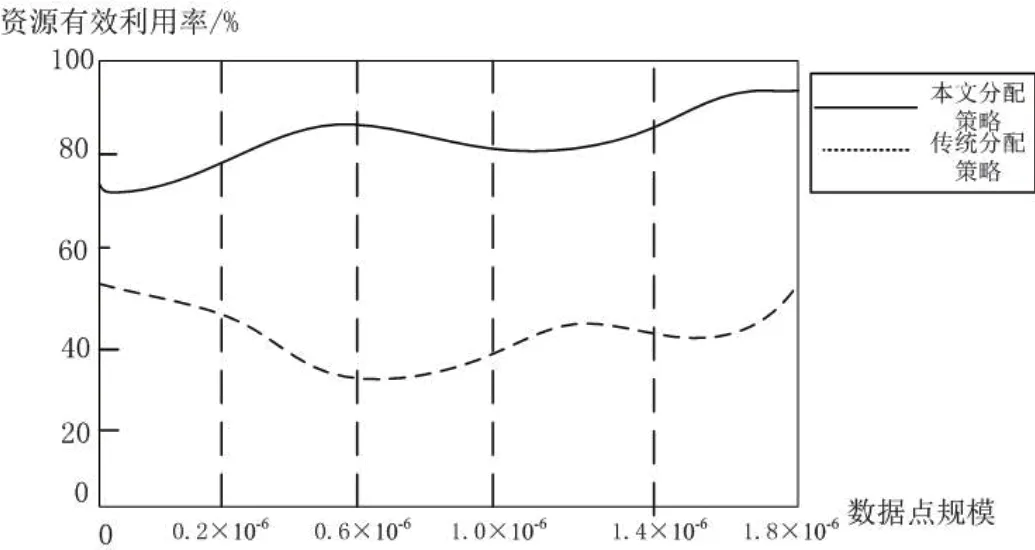
图1：实验结果对比图

公式（1）中，l 表示为所有数据块的集合；F 表示为传感器采样数据分配的结果；E 表示为传感器采样数据分配的转移矩阵。公式（1）中，转移矩阵E 的表达式为：

公式（2）应满足其自约束条件eij=1 或eij=0，其中j 的取值范围为1,2,3，…，m。

1.2 传感器静态数据分配

针对物联网中的传感器采样数据的静态分配主要是利用本文上述建立的物联网采样数据分配函数公式（1），利用传感器采样数据中的空间相关性，将采样数据块初始化并分配到各个存储器节点当中。通常情况下，数据块是以数据点的形式存储的，并且在每个数据点当中都能够支持全部数据类型，各个数据点所占据的空间大小基本相同。因此，根据这一特点，将本文上述的输入量l 进行简化，得到i=[i1，i2，i3，……in]T。由于数据模块在时域当中会对物理节点造成一定的负载动态影响，因此本文将数据模块放置在时域当中进行考虑。将简化后的输入量i 放置在固定的时域长度d 当中，从而得到i= [i1（t），i2（t），i3（t），……in（t）]T。面向物理网的传感器获取的采样数据是将连续变化的数据按照离散数值的方式表示。因此各个数据点的更新也处于离散化状态。本文选用泊松分布法对离散时间当中随机到来的概率分布进行表示，从而得到以下假设：

表1：影响传感器采样数据分配优先级因素对应表

假设每个传感器采样数据点在固定的时域当中更新的次数均符合参数相同的泊松分布，同时在分布式的环境中，物理节点通常是异构形态，因此定义多个物理节点中最大的负载量为Qmax=[Q（1，max），x（2，max），x（3，max），……x（m，max）]，则可以进一步得出在传感器存储节点单位负载率为：

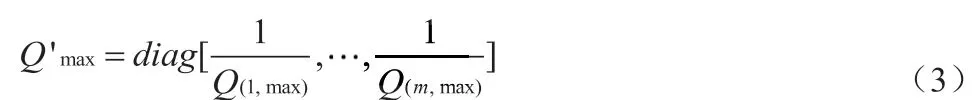
公式（4）中，F'表示为在每个传感器采样数据分量中每个物理节点在一定时域长度中的负载率，是一个由随机变量组成的数据量。根据负载平衡得出，输入量各分量之间的方差最小。因此可以将分配目标设置为求出F'期望的最小方差，即为传感器采样数据静态分配的最佳分配策略。

1.3 传感器动态数据分配

本文完成了对传感器采样数据的静态分配，但在实际应用中管理节点实时接收到的传感器存储节点的负载信息，还需要根据其动态的调整对数据分配，保证均衡负载。因此，根据这一条件，还需对传感器采样数据的动态分配进行设计[5-6]。首先将动态分配划分为两部分，其中第一部分为衡量存储节点是否超出负载能力；第二部分为调节过载存储节点的负载量。因此，对传感器采样数据进行动态分配的具体步骤为：获取传感器运行过程中每个存储节点的负载平均值，由此判定节点值计算结果，当该结果较小时，负载阈值与平均阈值相差较大，允许节点间负载波动，但不允许负载过热。随着负荷的增加，允许波动范围发生变化，允许负荷阈值与平均负荷之差随平均负荷的增加而减小[7]。最后，当平均负载数值过大时，则为了使有效负载信息最大化，则应设置固定的负载门限以及负载均值的差值，根据上述描述得出，传感器采样数据动态分布公式为：

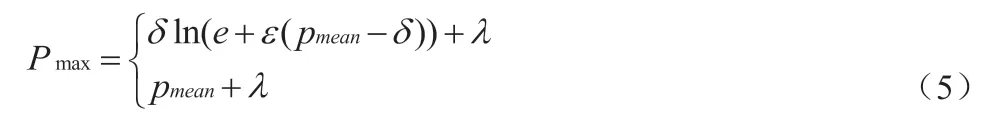
公式（5）中，Pmax表示为传感器存储节点过载门限数值；Pmean表示为各个传感器存储点负载率的平均值；δ 表示为衡量负载严重程度的临界门限；ε 表示为衡量低负载时的允许波动范围；λ 表示为当负载过重时固定负载门限值。当传感器过载存储节点中带有负载最大的数据点时，将该点分配到承担该负载后负载最小的存储点上，完成对传感器采样数据的动态分配。

2 实验论证分析

2.1 实验准备

为验证本文提出的面向物联网的传感器采样数据分配策略在实际应用中的效果，本文构建了一个虚拟的分布式实时数据库，数据库的管理节点，存储节点和数据收集中心分别建立在不同的虚拟物理设备上，传感器用于采集数据。为保证实验的可靠性，实验数据采用某地区水电站的真实数据作为实验样本，其中主要物理量包括电压、电流、水流量等。分别利用本文提出的分配策略与传统分配策略对传感器中的采样数据进行分配。

2.2 实验结果与分析

完成对比实验后，将两种分配策略得到的结果进行记录，并绘制成如图1 所示的实验结果对比图，比较本文提出的分配策略与传统分配策略分配后的数据有效利用率。有效利用率公式为：有效利用率=利用数据量/分配数据量×100%。将两种分配结果绘制成如图1 所示的实验结果对比图中。

根据图1 中的两条曲线对比可以看出，利用本文分配策略分配后的采样数据有效利用率明显优于传统分配策略。因此通过实验证明，本文提出的面向物联网的传感器采样数据分配策略在对采样数据分配时，合理性更高，更符合企业对资源利用率的需要。在实际传感器应用中，随着资源有效利用率的提高，企业相关经济成本的支出也会得到缓解，因此本文分配策略能够在保证有效分配的同时，提高企业的经济效益。

3 结束语

本文提出的传感器采样数据分配策略是针对物联网中数据连续变化性特点提出的，该策略中主要利用传感器的数据静态、动态特征，对数据分配进行优化。在后续的研究中还将对传感器采样数据兼顾查询更新操作进行进一步的研究，从而满足在更加频繁查询的情况下，实现对传感器采样数据分配的优化。