一花一世界 一叶一菩提*——单元视域下的章节起始课教学

胡蓓蓓

(江苏省无锡市市北高级中学,214000)

本文以章节起始课“任意角”为例,探讨如何在课堂中践行以核心素养为导向的起始课教学，供参考.

一、对教学内容的解读与目标指向

以《普通高中数学课程标准(2017年版)》为依据的新教材已于2019年下半年启用,新课程基于“立德树人、数学育人”理念,以核心素养为导向,落实“四基”,培养“四能”.“任意角”这一章节起始课正是培养学生用数学眼光看世界、用数学语言表达世界、用数学思维分析世界的难得素材.

1. 教材分析

授课内容为苏教版《普通高中课程标准实验教科书·数学(必修4)》第1章“三角函数”第1节“任意角”.学生已经在初中学习过锐角三角函数,对角和三角函数的定义有一定了解;并且在必修1中也已经学习了指数函数、对数函数、幂函数,这些函数刻画了生活中的某些规律.三角函数作为刻画客观世界周期性变化规律的重要模型,在教学中需渗透函数思想,体现全局观念.学生对角的认识很充分,这是本节课乃至本章三角函数学习的生长点,但原有角的认知并不能完全解释生活中的很多现象,角的范围需要扩充.

2. 教学目标和重点、难点

本节课的教学目标如下：

(1)能在教师创设的情境中认识到学习任意角的必要性,从而借助初中已有的知识经验将角的概念进行推广;

(2)能用恰当的图形语言和符号语言表示任意角;

(3)能理解象限角的概念及其终边相同的角之间的数量关系,能正确、熟练地从图形和代数两个角度判断一个角的终边位置;

(4)能体验和感悟到在任意角的建立和研究过程中所蕴含的抽象、从特殊到一般、类比、转化、数形结合、分类讨论等数学思想和思维方法,能体会到借助直角坐标系研究角的优越性.

本节课的教学重点为对任意角概念的理解；教学难点为终边相同的角的集合表示.

二、教学过程

概念教学应重视知识的形成过程,让学生在实践活动中体验知识的由来,增强分析问题、解决问题的能力,学会用数学的眼光看世界.

1. 概念引入

本节课分别从数学和生活两个角度揭示角的概念及范围推广的必要性:体操、跳水中的动作名称是从生活的角度阐述的,生活中存在大量循环往复、周而复始的现象;而利用圆周上的角表示点P的位置，则是从数学角度引入,即是否存在一个数学模型，可以用来刻画周期性问题中变量与变量的关系?

(1)创设情境:日出日落,寒来暑往,四季更替,生活中有很多这样周而复始的现象.比如转动的摩天轮,环绕一周需18分钟,6分钟后转120°,半小时后转600°,也有同学认为是240°,因为600°超出了初中认识的角的范围.通过这种思维的碰撞,教师引导学生思考:600°的角是怎样的一个图形呢?当然现实生活中还有很多这样的角,比如体操转体中的720°,540°等,都与学生头脑中的既有知识产生冲突,让学生感觉到有必要对角的概念进行推广.

设计意图三角函数的自变量是角,涉及到旋转以及数形结合等.选择转动的摩天轮作为熟悉的问题情境,抽象出最简单的周期变化模型——圆周运动,通过刻画圆周运动上点的位置变化,直观感受角的“任意性”,提升学生的数学抽象、数学建模和数学运算等素养.

(2)温故知新:初中是如何定义角的?

定义1平面内有公共端点的两条射线组成的图形.这是从角的最终形成结果给出的静态定义.

定义2平面内一条射线绕着端点从一个位置旋转到另一个位置所形成的图形.这个定义不仅呈现了角的最终形成结果,而且也给出了角的形成过程,是角的动态定义.

设计意图通过具体生活实例，打破学生原有的角不大于360的认知,思考如何完善角的概念,认识到学习任意角的必要性.

2. 概念生成

问题1你认为将一条射线绕其端点按逆时针方向旋转60°所形成的角,与顺时针方向旋转60°所形成的角是否相同?

设计意图为了体现规定的合理性,与正负数表示相反意义的量进行类比，与平面直角坐标系逆时针为正方向类比.类比是基本的数学思想方法之一,数学教学不仅要向学生传授知识与技能,更要传授思想和方法,培养学生的思维能力、创新意识和情感价值观,学会用数学的思维分析世界.

学生活动1画出30°,210°,-150°,-660°这四个角.

设计意图从认识生活中的角到学生画角,从感性到理性,自己动手,体验任意角的概念以及正负角的区别,强化本节课的教学重点,同时为更好地描述象限角、轴线角以及为引出终边相同的角的探究做好铺垫.在展示学生活动成果时,强调作图不仅要画出角的终边,还要呈现角的旋转过程,培养学生用恰当的图形语言和符号语言表示任意角的能力.

3. 概念深化

推广后的任意角在数学中如何刻画,怎样描述更加合理、方便呢?通常将角放到平面直角坐标系中,以角的顶点为坐标原点,角的始边为x轴正半轴,那么角的终边落在第几象限,就称这个角为第几象限角;如果角的终边落在坐标轴上,称为轴线角,轴线角不是任何象限角.

问题2判断以下说法是否正确:(1)锐角一定是第一象限的角;(2)第一象限的角一定是锐角;(3)第二象限的角一定比第一象限的角大.

引导学生总结:在平面直角坐标系中,给定角,就可以画出图形,就有唯一的终边与之对应;反之,给定终边,角不能唯一确定.

学生活动2请你写出一个正角、一个负角,并请同桌在平面直角坐标系中画出这两个角,判断分别是第几象限角.

预设生成:设置学生活动,在合作中加深对角的概念的理解,体会直角坐标系研究角的优越性.课前预设有学生会写出比较复杂的角,直接画图感到困难.引导学生思考:难道只能一圈一圈地旋转吗?学生产生内在驱动力,感觉到非常有必要去研究终边相同的角的关系.

学生活动3请同学们探究与210°终边相同的角的集合.

设计意图如何区别这些具有相同几何特征的角?体现了处理周期现象的一般原则.这对于学生是陌生的,理解有一定困难,但突破这一难点对深入学习本章知识十分重要.所以教师采取从特殊到一般的方式,引导学生作图发现这些角的终边旋转相差若干周,则在数量上相差k×360°.通过观察、猜想、归纳等一系列合情推理,得到终边相同角的关系的背后是数、形两个方面的阐释,既可以从代数(即数量关系)角度,也可以从几何(即图形特征)角度,由几何位置探讨其代数特征的“统一”,感受数学的整体性,学会用数学语言来表达世界.

4. 概念应用

例1在0°～360°的范围内,找出与-950°12′终边相同的角,并判断它是第几象限角?

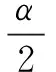
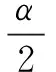
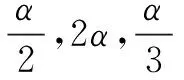
5. 归纳小结

本节课学习的主要知识有:任意角,象限角,终边相同的角.通过本节课的学习,体会两个主要核心思想:(1)如何确定一个角,不仅要关注形成的结果,还得关注形成的过程,在潜移默化中给学生渗透了任意角是“旋转出来的”这一本质;(2)把一个任意角不断地重复旋转(k×360°)得到无数个与它终边相同的角,这其实就是一种周期思想的萌芽,为学习本章内容做好前瞻性的铺垫,使本节课得到升华,而这也正是本节课的重点和难点.

设计意图这种“生长式小结”给出了本节课所在知识模块的地位,聚意点睛,让学生能从全局、整体角度感知本节课所学内容,注重知识的纵向发展和横向联系,凸显数学思想,提升数学素养.

三、对章节起始课的教学建议

弗赖登塔尔说“数学是充满联系的,不要教孤立的片段,应该教联系的材料”.数学概念的产生不是孤立的,而是人们在长期的生产实践中发现的,必然有其内在规律.所以帮助学生搭建认知结构,加强概念之间的联系,让概念理解从“孤立”存在变为“体系”存在,用联系的观点明确新概念研究的主要内容和基本研究方法,符合课程标准提出的如下要求：“把每堂课教学的知识置于整体知识的体系中,注重知识的结构和体系,处理好局部知识和整体知识的关系,引导学生感受数学的整体性”.

随着数学核心素养这一课程目标的提出,“单元整体教学” 成了数学课堂教学研究的热点,而章起始课就是在进入单元具体知识的学习之前,通过先行组织,系统建构出本章知识框架,帮助学生高屋建瓴地认识学习内容、形成认知结构,力求知识的融汇贯通.英国教育家怀特海曾说过:“教育使人通过树木见到森林”.章节起始课用整体的视角、联系的观点、发展的眼光看本章将要学习的内容,在理解教学、理解学生的基础上,运用行之有效的起始课教学策略,充分挖掘起始课的价值,让学生见木又见林,充分体验数学的“再发现”,完善知识体系,实现深度学习,从而发展学生的核心素养.