现代藏语信息熵的估算及语言模型的复杂度

完么扎西

（青海师范大学民族师范学院 青海省西宁市 810008）

1 引言

藏文是一种辅音音素拼音文字，即一种在文字体系中以辅音为主要成分的音素拼音文字。藏文辅音字母和元音符号拼写构成藏文（音节）字，藏文（音节）字构成词，词构成句子。所以研究藏文的信息熵时，既要研究藏文字符的信息熵，也要研究藏文（音节）字的信息熵，还要研究藏语词的信息熵。

国内外许多学者已经研究估测了多种文字的信息熵，如以字符为单位统计的英文、法文、德文、西班牙文和俄文等的信息熵分别为4.03 比特、3.98 比特、4.10 比特和4.01 比特。对于汉字信息熵的估算，采用了多种方法，冯志伟教授采用扩大汉字容量的方法，首次给出了汉字的信息熵为9.65 比特[1]；吴军采用一种统计的方法估测了汉语信息熵的一个上界，即5.17 比特[2]；孙帆等采用两种不同的统计方法，估计了汉字的极限熵值为5.31 比特[3]；黄萱菁等采用语言模型中稀疏事件的概率估计方法，估算了汉字的零阶熵、一阶熵和二阶熵，其值分别为9.62，6.18 和4.89 比特[4]。对于藏文信息熵的估算，也有了一定的研究，江荻采用一种统计的方法，在规模为20 余万字的藏文单语语料上计算了藏文字符的一阶熵、二阶熵以及多余度，其值分别为3.9913，1.2531 和0.766[5]；严海林等人采用一种概率统计的方法，在规模为4 千万字符的藏语单语语料上估计了藏文“字丁”的零阶熵、一阶熵、二阶熵和三阶熵，以及冗余度，其值分别为9.59、4.80、3.12、2.70 和0.72[6]；王维兰等人采用同样的方法估算了藏文“字丁”熵值[7]。完么扎西等人采用一种概率统计的方法，在规模为300 多万字的藏语单语语料上估测了藏文字符和藏文字的信息熵，其值分别为4.17 比特和8.21 比特[8-9]。

本文在文献[8]和[9]的基础上，通过N 元文法模型，建立了以藏文字符为基本单元的四元文法模型、以藏文（音节）字为基本单元的三元文法模型和以藏语词为基本单元的二元文法模型，并在不同的模型上估算了藏语的信息熵及其困惑度，从而得到了几种藏语语言模型的性能比较。

2 藏文字符和（音节）字

藏文是一种音素拼音文字。藏文有严谨的拼写规则，它不同于完全线性拼写的西方拼音文字。藏文既可以横向拼写，又可以纵向拼写，具有非线性的二维结构。

2.1 藏文字符

现代藏文字符共有169 种。经过统计发现，现代藏文书面语中比较常用的有辅音字母、反写字母、并体字母、元音符号、分字符、分句符、云头符、括号符和数字符号等共64 个字符[8]。

语言模型 C-M1C-M2 C-M3C-M4 S-M1 S-M2 S-M3W-M1W-M2信息熵 H 4.21 3.06 2.35 2.08 8.41 5.54 3.31 5.343.22困惑度 PP 18.5 8.3 5.1 4.2 340.1 46.5 9.9 40.59.3

图1：藏文字形的基本结构

2.2 藏文（音节）字

在传统藏文文法中，每相邻两个分字符之间的单位被定义为一个音节字以下简称藏文字。藏文字有一套严谨且完备的拼写文法，并具有一种独特的非线性二维结构，如图1所示。藏文字的拼写顺序是前加字、上加字、基字、下加字、元音字符、后加字、再后加字。藏文字形结构最少由一个辅音字母，即由单独一个基字构成，最多由6 个辅音字母构成，元音符号则加在辅音结构的上方或下方。

3 信息熵和语言模型的复杂度

根据信息论的理论，自然语言处理可以看作为通过获得的信息来消除句中文字的不确定性的过程。统计语言模型是描述自然语言不同语法单位的概率分布的模型，是自然语言处理的核心，它可以消除自然语言处理过程中的不确定性，但是不同的语言模型消除不确定性的能力不同。不同模型的差异，主要体现在语言中确定一个符号平均需要多少信息量，并且能够定量地描述各语言模型消除不确定性的能力。

根据香论（Shannon）的信息熵，可以定量地描述在不同的语言中，每个字符（藏语语言中藏文字符、藏文字或藏语词汇）到底包含多少信息。在自然语言处理中，信息熵表示语言的每个符号所含平均信息量的大小，是语言符号这个随机变量的不确定性程度的一种度量[10]。

藏语语言或该语言的子集可以看作为一个离散信源。若X 为离散随机变量（藏语语言中藏文字符、藏文字或藏语词语），则随机变量X 的取值集合及其概率测度pi分别为：

X= {x1,x2,…,xn}

pi= P[X=xi]

离散随机变量X 的概率空间为：

其中，pi（i=1,2,…,N）是语言符号ci（i=1,2,…,N）发生的概率。若语言符号ci的出现与上下文无关，且出现的概率相等，则该语言符号含有的信息量，即自信息量（H0）为：

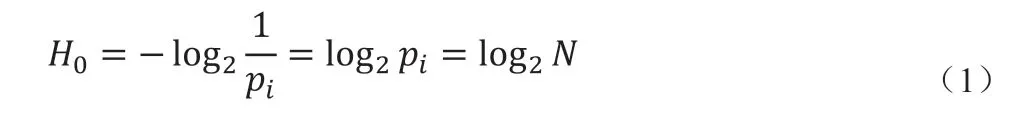
但是，藏语自然语言中，构成藏语句子的各语言符号ci出现的概率不可能相等。若暂不考虑语言符号ci的上下文相关性，则该语言符号ci含有的平均信息量为：

在信息论中，H 被定义为信息熵。容易证明H＜H0。

因为藏语自然语言中各符号出现的概率不相等，而且各个语言符号上下文相互关联，所以藏语自然语言可以看作为一个马尔可夫（Markov）链[11]。因此，可以引入n 阶Markov 模型来求解已知前面n-1 个语言符号时，后面出现的第n 个语言符号所含的平均信息量：

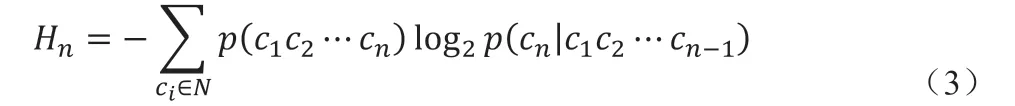
在信息论中，Hn被称之为条件熵。通过公式（3）可以计算出一阶条件熵、二阶条件熵、三阶条件熵、……等等，其计算公式分别为：

一阶条件熵：

二阶条件熵：

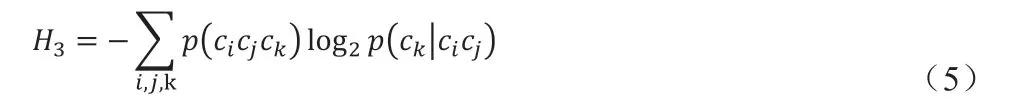
依此类推，可以计算出语言符号的任意阶条件熵。随着Markov 链阶数的增大，语言符号上下文信息体现得越来越丰富，条件熵也就越来越小。总是有：

另外，一个长度为n 的句子S（c1c2…cn）所含的信息量，可用如下公式计算：

在信息论中H(X)被定义为联合熵，那么信源中每个语言符号所含平均信息量，即平均信息熵为：

当阶数n 逐渐增加时，上述（3）式和（8）式都随着阶数n 的增加而呈非负单调递减，且有下界[12]，也就是说，当阶数n 逐渐增加时，熵逐渐趋于稳定而不再增加，此时，这个熵就是语言中一个符号所包含的信息量，叫做极限熵，即

（9）式反映了信源中每个符号的平均信息熵，即语言熵。因为自然语言是各太遍历、平稳的随机过程，由香论-麦克米兰-布莱曼定理可知，极限熵可由下式估计：

由于自然语言本身的复杂性和随意性，计算上述（3）式和（10）式比较复杂，甚至不太可能。但根据Markov 假设，将语言视为n-1 阶马尔可夫链。由此可建立一个N 元文法模型，即N-Gram 模型M。此时平均每个信源符号所含的信息量，即平均信息熵，记为H(PM)，并以PM（c1c2…cn）来近似（10）式中的p(cicj…cn)，其计算公式为：

由于无条件大于条件熵，所以有H∞≤H(PM)。因此，使用N-Gram模型M 得到的H(PM)是H∞的上界。换句话说，使用统计语言模型计算出的H(PM)的下确界是H∞，从而可以得到：使用N-Gram 模型M 得到的H(PM)越小，模型M 对自然语言的描述越精确[13-14]。H(PM)的物理意义是，已知历史信息的条件下，使用模型M 预测当前语言符号ci 出现的可能性只有种选择[15]。所以，称为语言模型M 的困惑度，记为pp：

语言模型的复杂度也叫困惑度，是语言模型M 描述自然语言能力的一种量度，困惑度越小，说明语言模型M 描述自然语言的能力越强，模型越有效。

4 基于统计语言模型的藏语信息熵估算方法

如前所述，影响统计语言模型性能的因素包括模型的阶数和构造模型的基本单元。显然模型的阶数越高则模型的性能越好，当然高阶模型的构造难度也越大。同时，构造模型的基本单元也很重要，例如在藏文中，建立语言模型时，可以以藏文字符为单元建立模型，也可以以藏文字为单元建立，还可以以藏语词汇为单元建立。因为现代藏文字符和藏文字的数目有限，以藏文字符和藏文字为单元可建立阶数较高的模型，如藏文字符的四元模型和藏文字的三元模型。现代藏语词汇的数目太大，而且尚未构建一种较好分词语料库，因而本文只建立了藏语词的二元模型。因此，本文实现的语言模型有基于藏文字符的一、二、三和四元文法模型（分别编号为C-M1、C-M2、C-M3和C-M4）、以藏文字为单元的一、二和三元文法模型（分别编号为S-M1、S-M2和S-M3）和以藏语词为单元的二元文法模型（分别编号为W-M2和W-M2）。

在建立语言模型时，由于训练语料的不规范，导致某些语言符号串(ci-k+1…ci-1ci)的出现次数可能为0，或者（13）式中的#(ci-k+1…ci-1ci)=1 和#(ci-k+1…ci-1)=1 而导致P(ci|ci-k+1…ci-1ci)=1，这个问题称为数据稀疏问题。解决这个问题的算法有很多种，其中以Good-Turing 估计、线性插值平滑、Katz 的回退式数据平滑最为典型和常用。根据文献[4]的研究结果，本文采用了Katz 的回退式数据平滑算法，该算法的公式使用方法见文献[16]和[17]。

通过上述所建立的语言模型可以实现对语言信息熵的近似估算，利用N-Gram 模型估算现代藏语信息熵的计算步骤分如下两步：

第一步：建立大规模藏语语料库，并对大规模藏语单语语料中的n 元同现概率进行统计，并估算公式（11）中的条件概率P(ci|ci-k+1…ci-1)。当语料足够大时，根据最大似然估计法和大数定理，有：

其中，#表示(ci-k+1…ci-1ci)和(ci-k+1…ci-1)在语料中出现的累计次数。

第二步：使用如下公式对H(PM)进行近似计算：

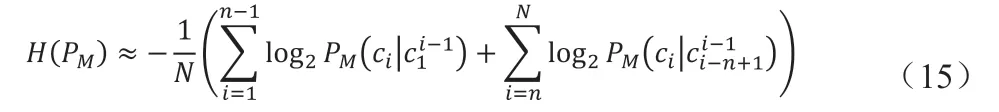
4 实验结果及分析

本文以涵盖藏文新闻、法律、现代公文、现代文学、藏医药和部分宗教文献等共300 多万字的大规模藏语单语语料为统计样本，应用上述公式（12）和（15）对现代藏语的信息熵进行估算，得到不同的语言模型所估计的现代藏语信息熵和困惑度如表1所示。

从表1 我们可以发现：

（1）随着模型阶数的升高，信息熵不断下降，这说明考虑上下文的影响越充分，计算结果越接近真实的值，就像文献[5]说的那样，以藏文字符为单元的模型阶数越高，信息熵越小，模型的多余度越大，其反映了字符之间存在严格的制约关系；

（2）不同的模型对语言描述的精确程度不同，所估计的信息熵或困惑度越小，表明模型对语言的刻画越准确；

（3）语言模型性能的好坏与模型单元和模型阶数都有关，表1 可知，一元词模型比二元字模型略好，但不如三元字模型，二元词模型比三元字模型好。

5 结论

本文引入信息论的方法研究了藏文信息熵。经过对300 多万字的藏单语语料进行统计，估算了不同语言模型的藏文信息熵，给出了一种应用语言模型计算藏语信息熵的方法。这个研究成果应用在计算机藏文快速输入法、藏文自动校对和藏文自动排序等藏文信息技术基础研究领域，取得了良好的效果。下一步的主要工作是进一步扩大语料规模，采用更巧妙的方法，计算更加精确的藏文极限熵。