板式无砟轨道锚穴部位损伤分布研究

2020-02-01任娟娟李家乐邓世杰徐家铎

铁道学报 2020年12期

任娟娟，李家乐，韦凯,邓世杰,3，王吉,3，徐家铎，3

(1.长沙理工大学交通运输工程学院，湖南长沙 410114； 2. 西南交通大学高速铁路线路工程教育部重点实验室，四川成都 610031；3.西南交通大学土木工程学院，四川成都 610031； 4.中国铁路上海局集团有限公司合肥工务段，安徽合肥 230012)

CRTSⅠ型板式无砟轨道以其高平顺、高稳定及少维修的特点得到广泛应用，但在运营过程中仍不可避免地产生损伤，其中轨道板裂纹损伤较为突出[1-2]。现场调研发现，轨道板裂纹在锚穴部位分布较为集中，且随着轨道结构服役时间的延长，裂纹会沿锚穴周边向轨道板表面扩展，其中严重者已经导致板角掉块，见图1。轨道板裂纹的扩展对轨道板结构受力及长期服役性能有较大影响，因此，有必要对此类裂纹的产生机制进行研究。

图1 轨道板锚穴部位裂纹扩展现场图

关于混凝土裂纹损伤的研究，文献[3]基于连续损伤力学理论，提出了结合混凝土断裂、损伤及刚度硬化的塑性损伤模型，并通过数值计算进行了验证。文献[4]提出了基于塑性理论的混凝土非线性分析模型，并利用试验数据进行了验证，该模型能够考虑混凝土材料弹性和塑性刚度退化的影响。文献[5]采用数值方法模拟预应力混凝土结构的使用、裂纹损伤演化直至失效断裂的过程，提出裂纹的形成会进一步增加混凝土的非线性行为。在无砟轨道领域裂纹损伤的研究方面，王平等[6]根据建立的弹性地基梁体有限元模型和车辆-轨道-路基垂向耦合振动模型，分析路基上轨道板开裂对车辆和无砟轨道结构的影响，认为轨道板开裂将影响无砟轨道的耐久性和使用寿命。杨洋[7]基于断裂力学理论，建立了考虑道床板内钢筋与混凝土滑移黏结的双块式无砟轨道力学及裂纹分析模型，分析了深度不同的道床板表面裂纹在温度梯度、轴向荷载、列车荷载作用下的失稳扩展。刘学毅等[8]针对无砟轨道连续道床板，按截面等效单元思路进行模型试验，测试各裂纹产生时的裂纹间距、轴向拉力、钢筋应力、裂纹宽度等。林红松等[9]根据双块式无砟轨道道床裂纹的特点，引入损伤函数表达道床裂纹，基于轮轨系统动力学理论，建立了考虑道床裂纹的车辆-无砟轨道耦合动力分析方法，就道床裂纹对双块式无砟轨道动力学响应的影响进行规律性探讨。吴欢[10]考虑了混凝土的弹塑性，建立了含裂纹的无砟轨道有限元计算模型，分析了列车荷载和温度荷载作用下无砟轨道受力、变形及裂纹张开量。

虽然上述文献对于混凝土损伤问题有较为明确的阐述，但大多针对混凝土或钢筋混凝土简易模型进行研究，与实际的轨道结构相差较大；虽有少数研究针对无砟轨道损伤问题，但其研究对象多为双块式无砟轨道，鲜有对CRTSⅠ型板式无砟轨道锚穴部位裂纹损伤的研究。本文主要根据遂渝铁路和渝怀铁路现场调研状况，基于损伤力学理论，应用混凝土塑性损伤模型，以最大主拉应力、拉伸及压缩损伤因子为评价指标，研究分析了轨道板生产预制过程中预应力施加对锚穴部位损伤的影响。

1 轨道板预应力的张拉施工过程

为准确模拟轨道板预制生产过程中锚穴周边混凝土的损伤状况，必须了解后张法预应力的施加过程。目前CRTSⅠ型板式无砟轨道所用的预应力体系为无黏结的预应力钢棒和锚固螺母，其预应力施加过程主要分为以下5个步骤：

(1)清理锚穴，保证锚穴内部无明显尘土及污物，见图2(a)。

(2)安装张拉杆和千斤顶，张拉杆由轨道板固定端穿入，从张拉端穿出，并与千斤顶对准，见图2(b)。

(3)张拉预应力钢棒，初始张拉力为10%σcn，并记录伸长值，然后进一步进油张拉，待达到张拉控制应力时保持荷载2 min，并记录伸长值，见图2(c)。

(4)旋紧锚固螺母，退出千斤顶，见图2(d)。

(5)灌注封锚混凝土填压，以保证预应力钢棒不因暴露于空气中而锈蚀。

图2 CRTSⅠ型板式无砟轨道轨道板预应力张拉过程

2 混凝土塑性损伤模型

2.1 混凝土塑性损伤模型理论

混凝土塑性损伤模型基于各向同性假设，采用弹性损伤结合受拉及受压塑性代替混凝土的非弹性行为[11]。在单轴往复荷载作用下，混凝土的塑性损伤演化和刚度恢复见图3。

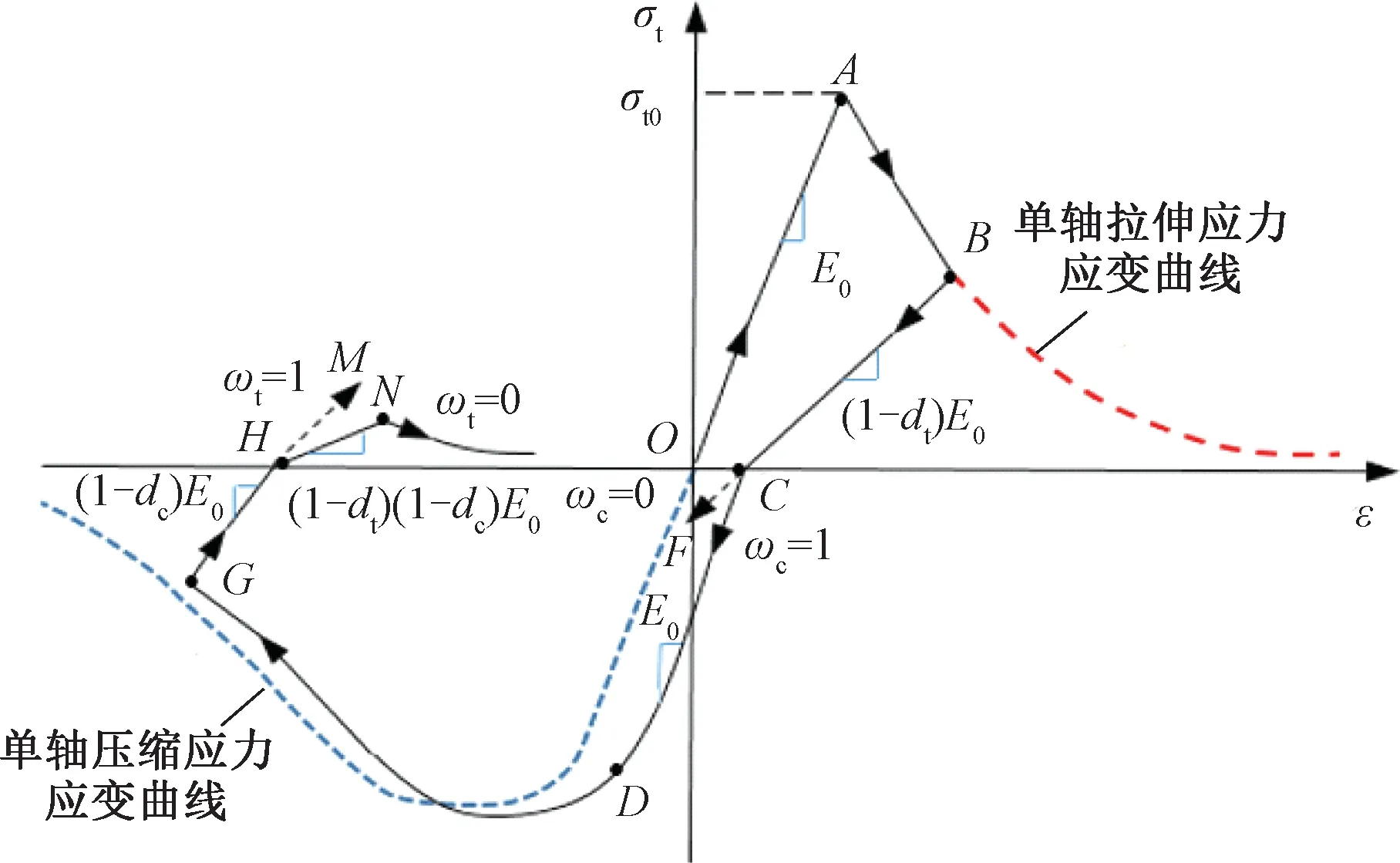
图3 混凝土弹性模量恢复示意

单轴拉伸时，混凝土先轴向受拉，拉应力呈线性增加，达到峰值拉应力(A点)时，混凝土开裂；继续加载至B点，开始卸载，混凝土将按有效刚度产生回弹，即图3中路径BC。当反向对混凝土施加轴压时，如果受压刚度恢复因子ωc=0，则按路径CF加载，如果受压刚度恢复因子ωc=1，则按路径CDG加载。当到达点G后，对其卸载再反方向加载拉伸，如果受拉刚度恢复因子ωt=1，则应力应变路径为GM，如果受拉刚度恢复因子ωt=0，则应力应变路径为GN[12]。

2.2 塑性损伤因子

混凝土塑性损伤模型假定混凝土材料主要因拉伸开裂和压缩破碎而破坏，通过定义混凝土本构关系和压缩、拉伸损伤因子描述其材料特性。受压损伤时，主要需定义非弹性应变与屈服应力和受压损伤因子之间的关系，其中受压损伤因子[13]为

( 1 )

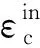
同理可得受拉损伤因子，轨道板所用C60混凝土非弹性应变与屈服应力和损伤因子之间的关系见图4，将此关系曲线导入模型便完成了对混凝土塑性损伤模型的定义。

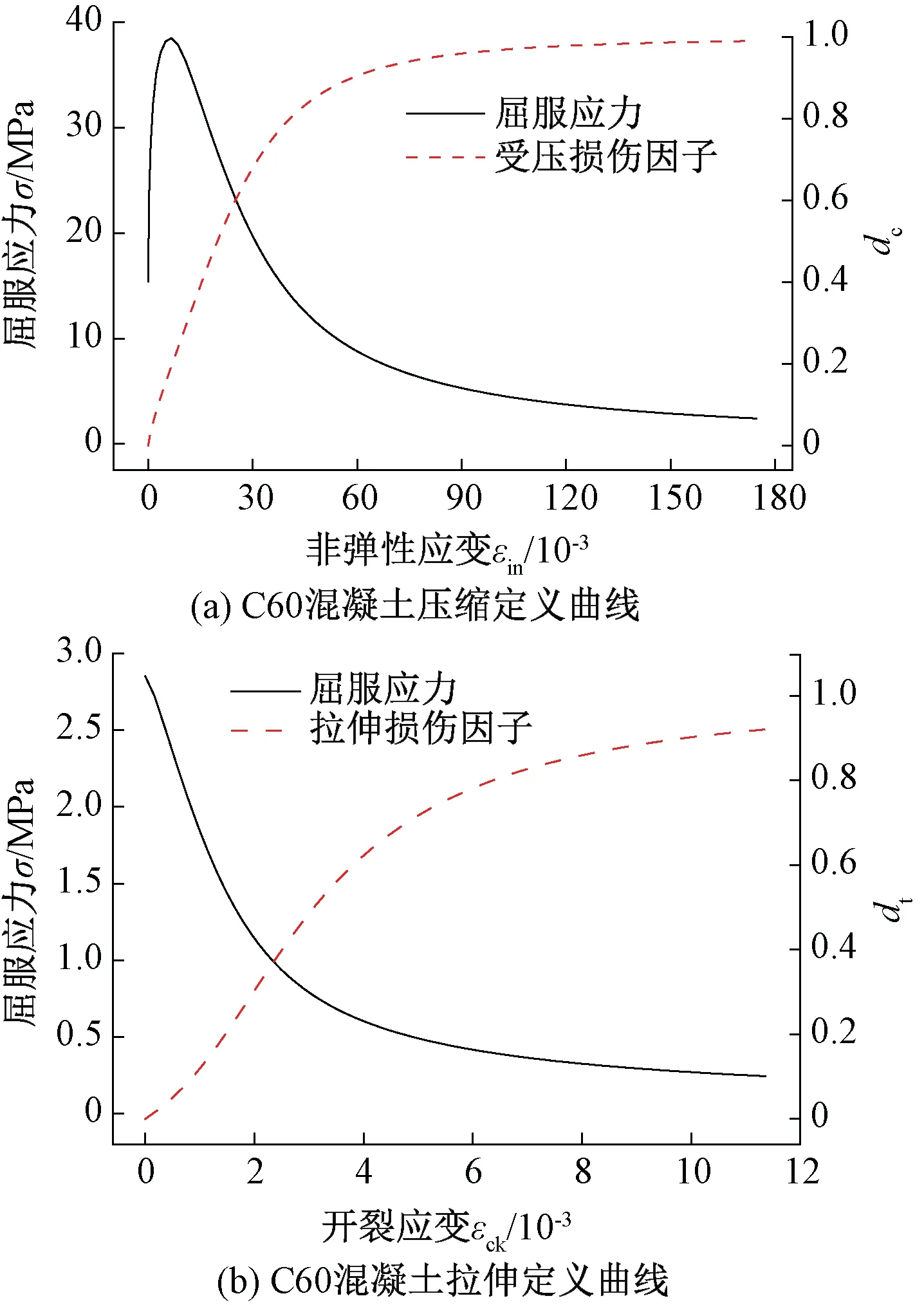
图4 混凝土塑性损伤模型定义曲线

图5 CRTSⅠ型板式无砟轨道锚穴示意

3 轨道板锚穴部位损伤分布模型

CRTSⅠ型板式无砟轨道锚穴分为纵向预应力锚穴和横向预应力锚穴，见图5，其中黑色圈表示纵向锚穴，红色圈表示横向锚穴[14]。虽然两者功能一致，但是在具体布置和构造上略有不同[15]，见图6，轨道板横向锚穴深度为60 mm，板厚为190 mm，锚穴边缘至轨道板上下表面距离为55 mm；纵向锚穴深度和总体宽度均为140 mm，锚穴边缘至轨道板上下表面距离仅为25 mm。

图6 轨道板预应力锚穴构造(单位：mm)

考虑到锚穴部位受力的复杂性，本文在模型中设置了轨道板的钢筋及预应力钢筋，见图7，轨道板的预应力体系包括横向和纵向预应力钢棒：横向预应力钢棒单层布置，位于轨道板中轴线处，共16根；纵向预应力钢棒双层布置，对称布置于轨道板中轴线两侧，中心距80 mm，每层6根，共12根。普通钢筋布置于轨道板上下两层，混凝土保护层厚度取为40 mm。

图7 CRTSⅠ型板式无砟轨道轨道板钢筋布置(单位：mm)

本文分别考虑纵向和横向预应力对锚穴部位损伤分布的影响，考虑纵向预应力时取轨道板沿线路纵向半结构进行模拟，考虑横向预应力时选取轨道端部3个锚穴长度的轨道板进行模拟[16]。在建模过程中，轨道板采用C3D8R单元模拟，网格尺寸为10～50 mm(在锚穴附近采用较小的网格尺寸)；锚固垫板采用解析刚体单元，忽略预应力的损失；普通钢筋与预应力钢棒均采用T3D2单元模拟，网格尺寸为50 mm；预应力采用降温法施加，其中横向预应力钢棒设计张拉力为127 kN，纵向预应力钢棒设计张拉力为122 kN[17]，并通过将预应力钢棒两端节点与轨道板锚固垫板的绑定约束来模拟无黏结预应力的作用；普通钢筋通过嵌入命令实现与轨道板的联系；约束轨道板的竖向位移，考虑到凸台的作用是约束轨道板纵向伸长，不约束其纵向收缩变短，而本文荷载只涉及张拉预应力，故忽略凸台结构对轨道板拉压变形的影响，仅对板下表面中部施加纵横向位移约束。轨道板弹性模量Es=36 GPa，泊松比μs=0.2；普通钢筋弹性模量Er=200 GPa，泊松比μr=0.3；预应力钢筋弹性模量Ep=200 GPa，泊松比μp=0.3，直径R=13 mm,所建模型见图8。

图8 轨道板锚穴部位有限元模型

4 锚穴部位最大主拉应力和损伤因子分析

4.1 锚穴部位最大主拉应力分析

无论材料处于何种应力状态，只要最大拉应力达到其拉伸断裂时的最大拉应力值，则材料破坏[18]。本节研究纵横向预应力作用下，轨道板锚穴部位最大主拉应力分布状况，以判断其是否开裂。由图9可知，纵横向预应力作用下轨道板最大主拉应力值分别为2.47 MPa和1.92 MPa，考虑到C60混凝土的轴心抗拉强度标准值为2.85 MPa[19]，纵横向预应力作用下轨道板锚穴部位所受最大主拉应力已基本达到C60混凝土抗拉强度标准值的87%和67%，且纵向预应力作用下轨道板表面仍有2.4 MPa左右拉应力，因此，相较于横向锚穴，纵向锚穴更容易因受拉产生初始裂纹损伤。

图9 纵横向锚穴部位最大主应力分布(单位：Pa)

4.2 锚穴部位压缩损伤因子分析

混凝土塑性损伤模型的核心之一是对混凝土压缩损伤因子的分析[20]，图10为轨道板在纵横向预应力作用下锚穴部位压缩损伤等轴侧视图。由图10可知，纵横向压缩损伤最大值均分布于锚固板背后，横向锚穴部位压缩损伤沿轨道板深度方向共延伸20 mm左右，纵向锚穴部位压缩损伤沿轨道板深度方向共延伸30 mm左右。

图10 纵横向锚穴压缩损伤等轴侧视图

图11(a)、图11(b)分别为纵横向压缩损伤最严重截面的正视图，由图11可知，损伤皆呈环形分布于锚穴两侧，并逐渐向轨道板内部发散，其最大压缩损伤因子均小于0.5。

图11 纵横向锚穴压缩损伤最严重截面正视图

4.3 锚穴部位拉伸损伤因子分析

由于混凝土是典型的抗压不抗拉的工程复合材料，其拉伸损伤因子是表征损伤程度的重要指标，因此本节主要对轨道板锚穴部位拉伸损伤因子进行分析。图12(a)为轨道板横向锚穴部位拉伸损伤等轴侧视图，由图12(a)可知，拉伸损伤相较于压缩损伤范围更大，损伤沿轨道板深度延伸35 mm左右；图12(b)为拉伸损伤最严重的截面，从图12(b)可以看出，拉伸损伤同样沿锚固板呈环形放射状向外发散，并且不断衰减，损伤最为严重区域位于锚固板边缘，最大拉伸损伤因子可达0.9，但损伤并未延伸至轨道板表面。因此，拉伸损伤相较于压缩损伤更为严重，且较容易在锚固板边缘产生初始裂纹损伤。

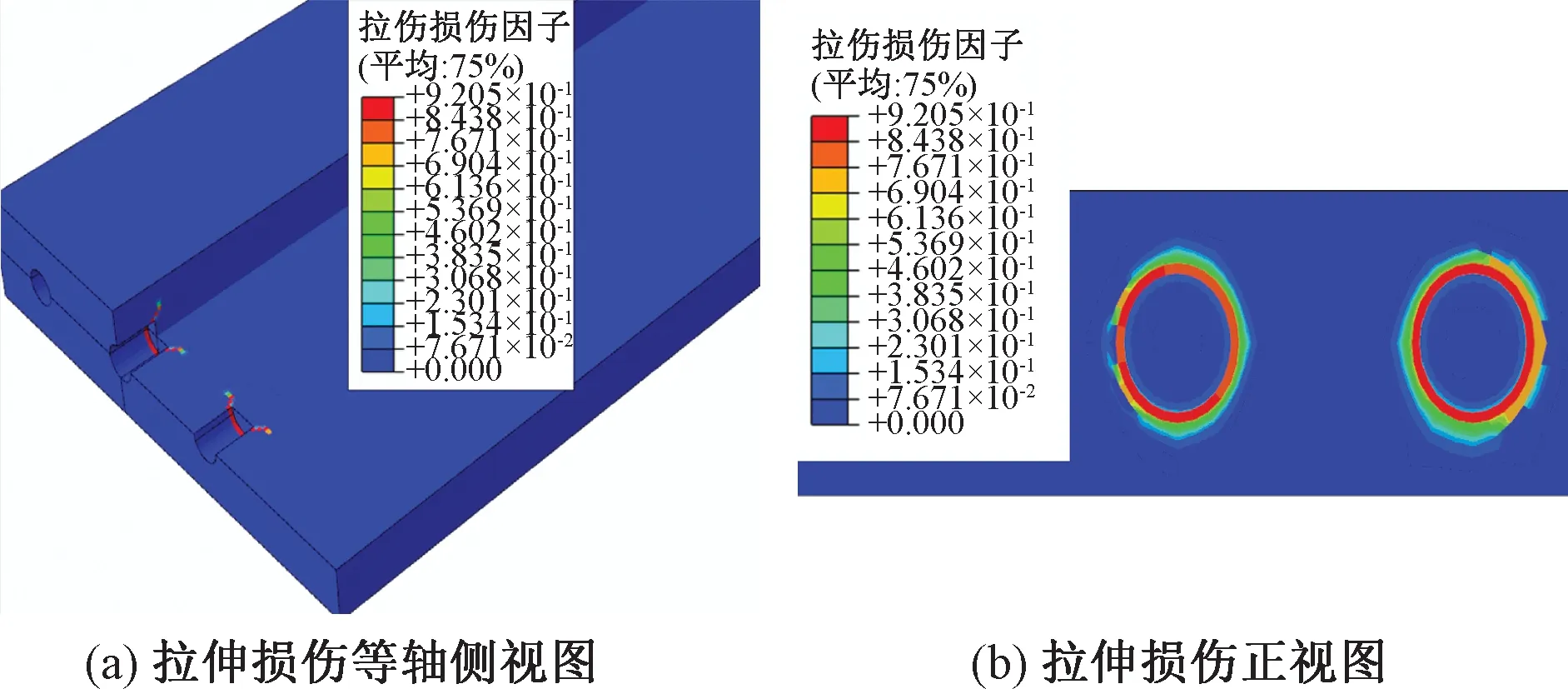
图12 横向锚穴部位拉伸损伤分布图

为进一步研究横向预应力作用下锚穴部位拉伸损伤在轨道板内部的分布情况，沿模型纵向剖切若干截面，其距板边的距离为a，取a值分别为72、80、88、96、104和112 mm，见图13中红色剖切线。

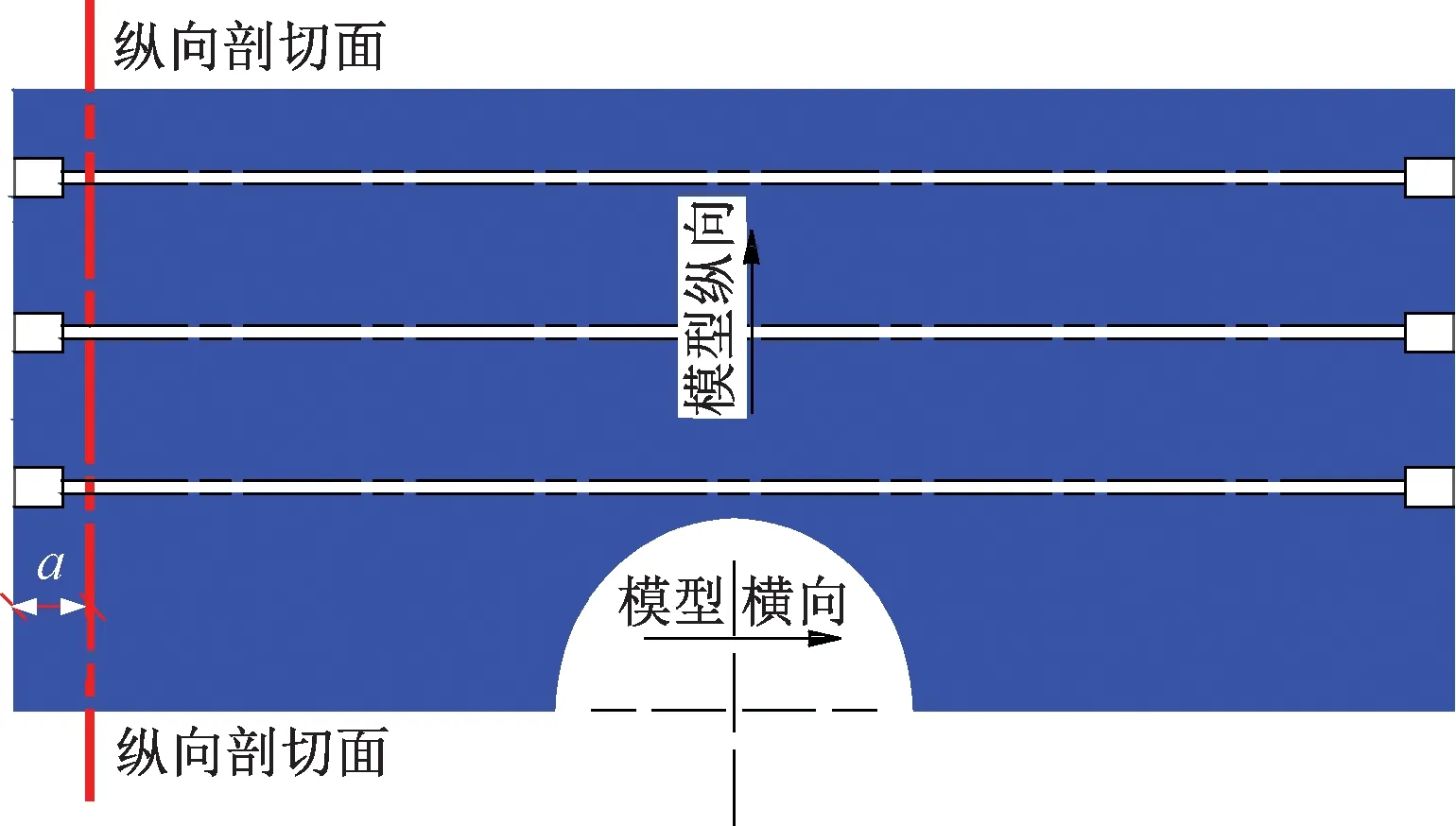
图13 轨道板横向预应力分析示意

横向预应力作用下锚穴部位拉伸损伤各纵向剖切面见图14，当a=72 mm时，见图14(a)，由于横向锚穴深度为80 mm，此剖切面上并未出现拉伸损伤；a=80 mm时，见图14(b)，拉伸损伤开始出现，并且沿锚固板边缘轨道板拉伸损伤因子已达到0.9，材料已基本接近失效；当a=88 mm和96 mm时，见图14(c)、图14(d)，拉伸损伤以环形放射状向轨道板内部扩展，扩展范围约为20 mm，最严重部位拉伸损伤因子仍然达到了0.9；当a大于96 mm时，见图14(e)、图14(f)，轨道板拉伸损伤开始衰减，并最终消失。

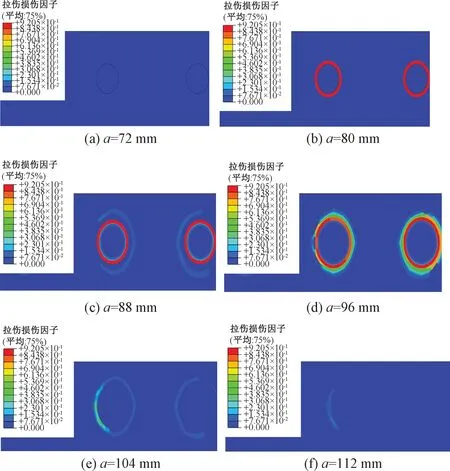
图14 轨道板各纵向剖切面拉伸损伤分布图

通过图14的分析可知，横向预应力作用下锚穴部位的拉伸损伤出现在横向锚穴深度80 mm前后，锚固板边缘损伤程度可达0.9；在锚穴深度大于96 mm时，锚穴部位的损伤程度和损伤范围逐渐减小并消失，拉伸损伤最大影响深度为30 mm左右。

图15为纵向预应力作用下轨道板锚穴部位拉伸损伤分布，从图15(a)可以看出，拉伸损伤相较于压缩损伤范围更大，且其延伸范围已经到达轨道板表面；图15(b)为拉伸损伤最严重的截面，从图15(b)可以看出，拉伸损伤同样沿锚固板呈放射状向外发散，并不断衰减，损伤最为严重区域位于锚固板边缘，最大拉伸损伤因子可达0.9，损伤极为严重。因此，纵向预应力作用下，锚穴部位拉伸损伤程度更高，极有可能在预应力施加阶段便产生初始裂纹损伤。

图15 纵向锚穴部位拉伸损伤分布

为进一步研究纵向预应力作用下锚穴部位拉伸损伤在轨道板内部的分布情况，沿模型横向剖切若干截面，其距板边的距离为b，取b值分别为150、160、165、170、175、180 mm，见图16中红色剖切线。

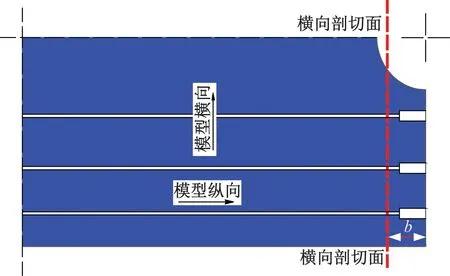
图16 轨道板纵向预应力分析示意图

纵向预应力作用下锚穴部位拉伸损伤各横向剖切面见图17。当b=150 mm时，见图17(a)，由于纵向锚穴深度为160 mm，此剖切面上并未出现拉伸损伤；当b=160 mm时，见图17(b)，拉伸损伤开始出现，并且沿锚固板边缘拉伸损伤程度已经达到了0.9，损伤范围呈放射状向轨道板表面扩展；当b=165 mm时，见图17(c)，拉伸损伤沿锚穴边缘扩展到轨道板上下表面，轨道板表面的拉伸损伤因子仍高达0.73；当b=170、175 mm时，见图17(d)、图17(e)，拉伸损伤随着向轨道板内部及上下表面的延伸而逐渐衰减，损伤程度逐渐变小；当b大于180 mm时，见图17(f)，轨道板拉伸损伤已逐渐消失。

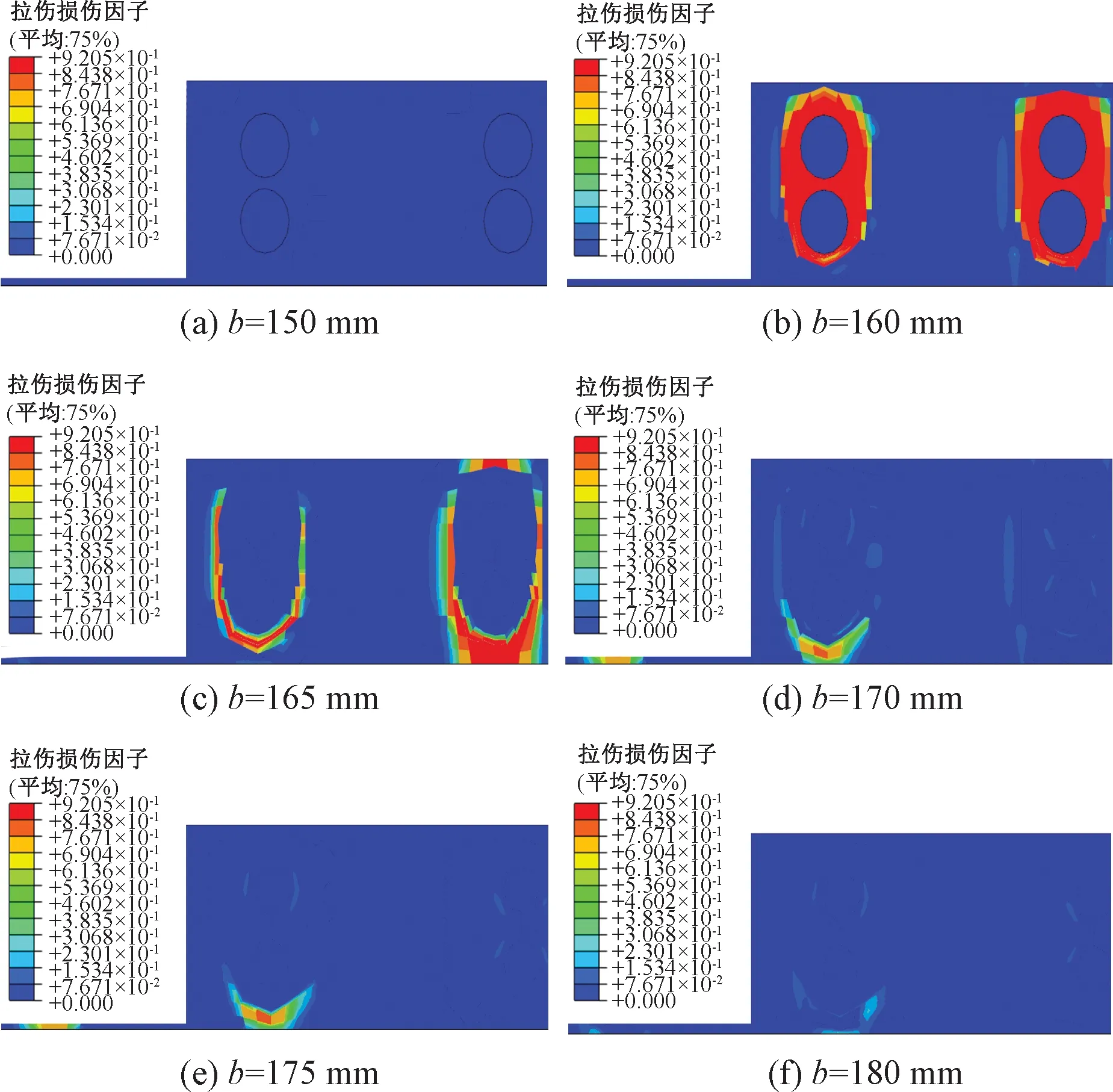
图17 轨道板各横向剖切面拉伸损伤分布图

通过图17的分析可知，纵向预应力作用下锚穴部位拉伸损伤出现在纵向锚穴深度160 mm前后，锚固板边缘损伤程度已达0.9，损伤范围几乎到达轨道板上下表面，较容易在纵向锚穴边缘及轨道板表面区域内形成初始裂纹损伤。在锚穴深度大于170 mm时，锚穴部位的损伤程度和损伤范围逐渐减小直到消失，拉伸损伤最大影响深度为30 mm左右。