基于深度强化学习算法的空间漂浮基机械臂抓捕控制策略

2020-02-01王耀兵杜德嵩齐乃明

载人航天 2020年6期

孙康，王耀兵，杜德嵩，齐乃明

(1. 哈尔滨工业大学航天工程系，哈尔滨 150001； 2. 北京空间飞行器总体设计部，北京 100094)

1 引言

随着人类航天活动的逐年增加，空间飞行器的数量呈现快速增长趋势[1]。在轨航天器由于使用寿命有限，零部件故障或意外碰撞等原因而无法正常运行，从而形成非合作的失效航天器或称太空垃圾，通常还带有一定程度的翻滚特性[2]。失效航天器的及时捕获、接管、修复或清理等对于正常在轨运行航天器的安全以及轨道资源再回收等有重大意义。

空间机械臂因其具有质量轻、灵活性高、操控性强等优势，在空间失效目标的捕获任务中具有广泛的应用前景[3-4]。为实现抓捕过程的稳定可靠，应使空间机械臂在接近目标抓捕位置时平稳，且相对速度应尽可能小，从而减小抓捕碰撞力。国内外学者针对抓捕过程空间机械臂的控制策略进行了诸多研究。Yoshida等[5-7]研究了针对空间机械臂的在轨动力学与控制问题，并在ETS-VII任务中进行了实际应用；Matsumoto等[8-9]对捕获空间失效航天器的路径规划和捕获过程的动力学进行了研究；Angel等[10-11]针对空间翻滚目标的抓捕任务，通过控制空间机械臂的接近速度，使其与目标的相对速度通过抓捕系统的质心，实现了基座姿态扰动最优；Yu等[12]针对带有柔性帆板的空间漂浮机械臂的动力学建模和非合作目标的抓捕任务进行了研究；Xu等[13]针对空间机械臂的运动学、动力学和末端执行器存在的不确定性问题，提出一种改进的自适应反步控制器 (Backstepping Controller)，保证了传统动态曲面控制方法跟踪误差的渐近收敛性。上述针对空间机械臂的抓捕控制均基于多体系统动力学模型来实现，而多体系统的动力学模型很难被精确建立，特别是针对带有柔性帆板、柔性臂杆等结构的航天器，严格按照动力学模型实现抓捕控制会产生较大的位置和速度偏差，从而产生抓捕逃逸或碰撞力过大等问题。

强化学习(Reinforcement Learning，RL)算法在机器人系统控制中的应用近年来逐渐兴起，并取得了较好的应用[14]。Smrui[15]基于深度强化学习算法(Deep Reinforcement Learning, DRL)对机械手臂的多种操作任务进行了研究，同时介绍了DRL针对高维状态空间的目标逼近策略的实验室级的应用；Wang等[16]基于深度强化学习算法对轮式机器人在斜坡路面上的动态路径规划进行了研究，并与传统的依靠动力学模型的D*规划算法作对比，仿真结果证明了深度强化学习算法能在保证精度的前提下较快地实现动态路径规划。

DRL算法具有不依赖系统运动学或动力学模型的特点，通过设定奖赏函数实现机器人系统的运动轨迹及驱动力矩控制，对于空间非合作目标的多自由度机械臂抓捕问题有较好的适用性。本文基于DRL算法提出一种深度确定性规则策略(Deep Deterministic Policy Algorithm, DDPG)，将空间非合作目标的抓捕过程的漂浮基机械臂的位置、力矩和速度控制问题转化为高维空间的目标逼近问题，通过设置目标奖赏函数，驱动空间机械臂的末端位置和运动参数满足抓捕条件，从而实现稳定可靠抓捕。

2 物理模型及坐标系定义

图1为漂浮基空间机械臂抓捕空间非合作目标的物理模型。空间机械臂具有n自由度，一端与漂浮状态的本体星连接，非合作目标为带有自旋特性的空间漂浮物体。FI(OXYZ)为系统惯性坐标系；F0(o0x0y0z0)为本体星质心坐标系，其原点位于本体星质心位置；Fi(oixiyizi)为空间机械臂关节i的中心坐标系，qi(i=1,…,n)为关节i的转角，关节转动方向zi(i=1,…,n)与关节转轴平行；Fe(oexeyeze)为空间机械臂末端抓捕机构中心坐标系；Ft(otxtytzt)为非合作自旋目标质心坐标系；Fh(ohxhyhzh)为非合作目标的抓捕位置中心坐标系；ωt为目标自旋角速度；R0为惯性系下的本体星质心矢径；Ri(i=1,…,n)为惯性系下关节i中心坐标系的原点矢径；Re为惯性系下的空间机械臂末端机构中心坐标系的矢径；Rt为惯性系下自旋目标的质心矢径；r0为关节1的中心坐标系F1在基座质心坐标系F0下的矢径；rh为Ft到Fh的矢径；di(i=1,…,n)为臂杆i+1的始末点矢径(由Fi指向Fi+1)。

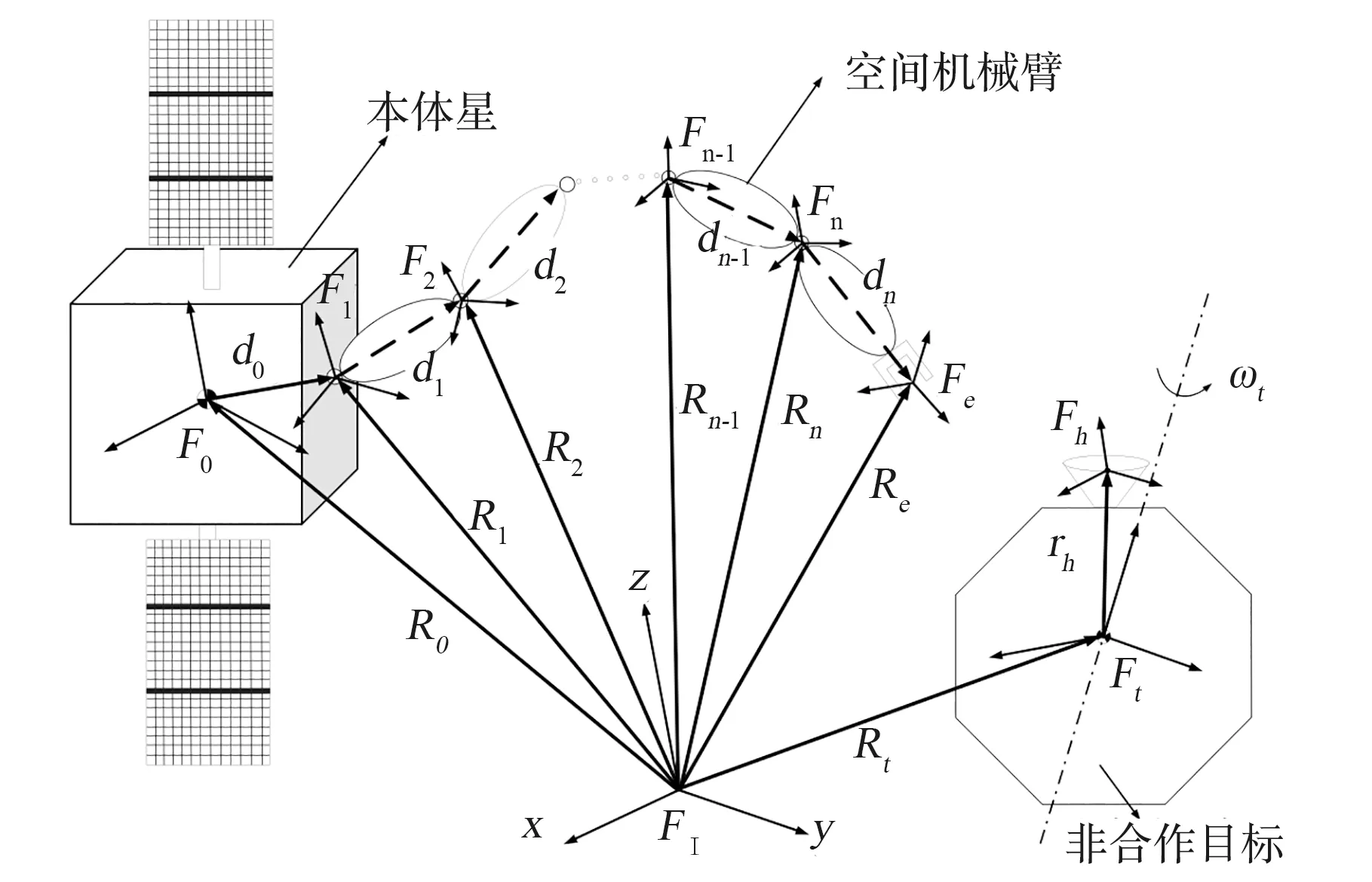
图1 空间漂浮基机械臂非合作目标抓捕物理模型Fig.1 Physical model of free-floating space manipulator capturing uncooperative target

3 基于DRL算法的抓捕控制策略

利用代理(Agent)的思想实现对漂浮基座的空间机械臂进行抓捕控制，将控制指标作为奖赏函数的变量，利用代理对空间机械臂的关节运动进行控制，并将奖励值最为运动方向的控制反馈，逐步训练，使空间机械臂满足抓捕条件。

3.1 DRL算法基本原理

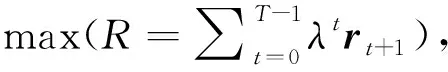
1)定义状态空间S={s0,s1,…,sn}，起始时刻的状态s0及其所对应的概率分布P(s0)；

2)定义行为空间A={a0,a1,…,an}；

3)定义环境的动态更新驱动函数p(st)；

4)定义行为奖赏函数R(st,at,st+1)；

5)定义奖赏折扣系数λ∈[0,1]，用于强调即时的回报。

图2 深度强化学习算法的状态-行为-学习循环框图Fig.2 State-action-learning loop of DRL algorithm

DRL算法具有局部决策独立与整体历程的基本特性，即当前环境状态st仅与前一时刻的环境状态st-1和行为at-1有关，而与此前0时刻到t-2时刻对应的环境状态和行为均无关。DRL算法的这种特性满足Markov离散随机变量的概率分布特性，因此其深度强化学习的过程也可称为Markov过程，数学表述如式(1)：

p(st|a0,a1,…,at-1,s0,s1,…,st-1)=p(st|at-1,st-1)

(1)

空间机械臂系统包含自由漂浮基座和n自由度空间机械臂两部分，根据DLR控制策略的构成要素，定义漂浮基座对应的状态空间集合为式(2)：

(2)

(3)

定义t时刻各关节对应驱动力矩为式(47)：

(4)

定义空间机械臂末端抓捕机构与空间非合作自旋漂浮目标的距离在时刻t时为式(5)：

dt=|Re-Rt|

(5)

以完成捕获任务的时间、机械臂末端抓捕机构距离目标点的距离、关节观测驱动力矩大小为奖赏值的参考指标，定义奖赏函数如式(6)：

rt=f(t)[l1g(dt)+l2h(|τt|)]

(6)

其中，f(t)为与捕获时间相关的指标函数，g(dt)为与机械臂末端抓捕机构距离目标点的距离的指标函数，h(|τ|)为与机械臂的关节控制力矩相关的指标函数；l1、l2分别对对应函数的调和系数。为使训练过程更加有效，应使得抓捕任务的整个过程奖励值随着相对应的指标的变化均有明显波动，因此设置上述各指标函数如式(7)：

(7)

其中，f(t)、g(dt)、h(|τt|)具有相同的函数形式，对于如式(8)所示形式的函数：

(8)

式(8)求一阶导并取绝对值得式(9)：

(9)

显然，在Δ接近0或者远离0时，Γ(Δ)对应的函数值波动范围均较大。同理，式(7)中各函数在远离或接近对应指标的情况下，奖励函数rt均会产生较为明显的波动，可促使训练更加有效，从而减少训练收敛次数，加快目标的抓捕进度。

3.2 DDPG算法模型

DDPG算法是对确定性策略算法(Deterministic Policy Algorithm, DPG)算法的改进。DPG算法包含行为函数λ(s|q)以及价值函数J(s,a)两部分，算法通过评价函数对离散时刻的行为进行评价，以求得行为的确定性状态。为了实现对行为的逐步更新，定义与行为参数相关的链式规则函数如式(10)：

(10)

价值函数J(s,a)通过式(11)所示Bellman方程实现逐步更新：

BJ=E[y-J(s,a|qJ)2|s=st,a=λ(st|qλ)]

(11)

漂浮基座的空间机械臂抓捕非合作自旋目标属于高维连续空间问题，无法直接用QL(Q-Learning)算法解决。图3所示为DDPG控制算法的结构流程图，在DDPG算法中，定义目标价值函数J′(s,a|qJ′)和目标行为函数λ′(s|qλ′)，上述两目标函数用于分别计算目标值。目标网络的权重通过下式(12)实现软更新，可有效避免直接引用前一步计算结果所带来的训练结果超调、目标不收敛等问题，提高算法训练过程的稳定性。

(12)

图3 DDPG算法的结构流程图Fig.3 Structure schematic diagram of DDPG algorithm

3.3 预演练DDPG控制策略

对于包含高维度的状态空间和行为空间的非合作目标捕获问题，直接利用DDPG算法对空间机械臂的抓捕任务进行控制，由于数据量和计算量极大，训练模型效率和收敛时间均不理想。因此，本文利用包含预演练(Pre-traing, PT)过程的DDPG控制策略[18]。PT策略是指预先训练空间机械臂进行主动随机运动，训练过程产生的状态转换函数存储至重放缓冲集合{R}。PT过程并不包含参数更新的步骤，因此较短时间内可对空间机械臂进行大量的训练，使得空间机械臂在训练前就具有大量学习数据作为参考。此方法可显著提高DDPG算法在高维度状态空间和行为空间的训练效率，缩短收敛时间。

4 仿真分析

4.1 仿真初值

利用漂浮基座空间三自由度机械臂抓捕空间非合作自旋目标的模型进行仿真分析，目标为空间自由漂浮状态，且存在自旋特性。表1为漂浮基座空间机械臂的零位对应D-H参数。表2为漂浮基座空间机械臂各模块以及非合作自旋目标的质量和惯量参数，其中m0、m1、m2、m3、mt分别为漂浮基座、臂杆1、臂杆2、臂杆3、非合作目标的质量，Ixx、Ixy、Ixz、Iyy、Iyz、Izz为对应的惯量矩阵。需要特别说明的是，表中非合作目标的惯量参数是在Fh坐标下表示的。假设目标的抓捕位置位于目标自旋轴上，且抓捕过程的最后阶段，空间机械臂末端抓捕机构的速度方向与目标自旋轴重合，降低实际抓捕难度。

表1 零位D-H参数

表2 质量和惯量参数

目标抓取点位置为Rh=[0.75 0.15 1.85]Tm。式(5-5)对应的奖励函数中，设置l1=0.05，l1=0.1；设置奖赏累加折扣系数λ=0.85；批量参考数组个数n=20；行为网络λ(s|q)与J(s,a|qJ)设置为3层，每层单元个数分别为100，100，20，神经网络的LR参数(Learning Rate，学习率)设置为10-4；训练次数为1000；目标行为网络与目标评价网络更新步间距分别为100和150；其余参数设置参照文献[17]，此处不再赘述。

目标抓捕成功的条件设定如下：①末端抓捕机构冗余误差设定为0.05 m，定义目标球形抓捕域的半径为SR=0.05 m，即抓捕位置中心点坐标与末端抓捕机构中心距离误差εt≤SR；②且|τt|2≤1 N·m时，抓捕机构实施收拢动作并完成目标捕获；③抓捕机构与目标抓取点的相对速度小于0.05 m/s。

4.2 仿真结果

仿真工具为MATLAB R2017b，设置仿真步长为0.05 s，仿真结果如下：图4分别为加入PT训练策略和未加入PT训练策略的训练历程，由奖励值曲线变化对比可知，包含了PT训练策略的DDPG训练在经历600次训练历程后，总奖赏值趋于稳定，约为150，对应为控制策略逐渐收敛至目标要求；而不包含PT训练策略的DDPG训练在经历1000次训练历程后，奖赏值未达到100且仍处于振荡状态，未能收敛。因此，通过PT训练策略可有效提高训练效率，缩短非合作目标抓捕任务所需时间。因此，采用包含PT训练策略的DDPG控制算法训练FFSM完成非合作自旋目标的捕获，仿真结果如图5～9所示。图5为3个关节训练历程的角度和角速度变化曲线，图6为抓捕过程3个关节训练历程的输出力矩曲线，图7为空间机械臂末端点的抓捕过程三维轨迹，图8为空间机械臂抓捕距离及与目标的相对速度变化曲线图，图9为漂浮基座在抓捕过程中的位置和线速度、角度和角速度变化曲线。

图4 DDPG训练历程奖励值变化曲线Fig.4 Curves of reward value with DDPG training times

图5 关节角度和角速度曲线 Fig.5 Angle and angular velocity of three joints

图6 关节力矩曲线图Fig.6 Control torque of three joints

图7 机械臂末端抓捕机构中心三维轨迹图Fig.7 3D trajectory of end effector of FFSM

图8 机械臂末端抓捕距离及相对速度曲线图Fig.8 Distance and relative velocity between end effector of FFSM and target

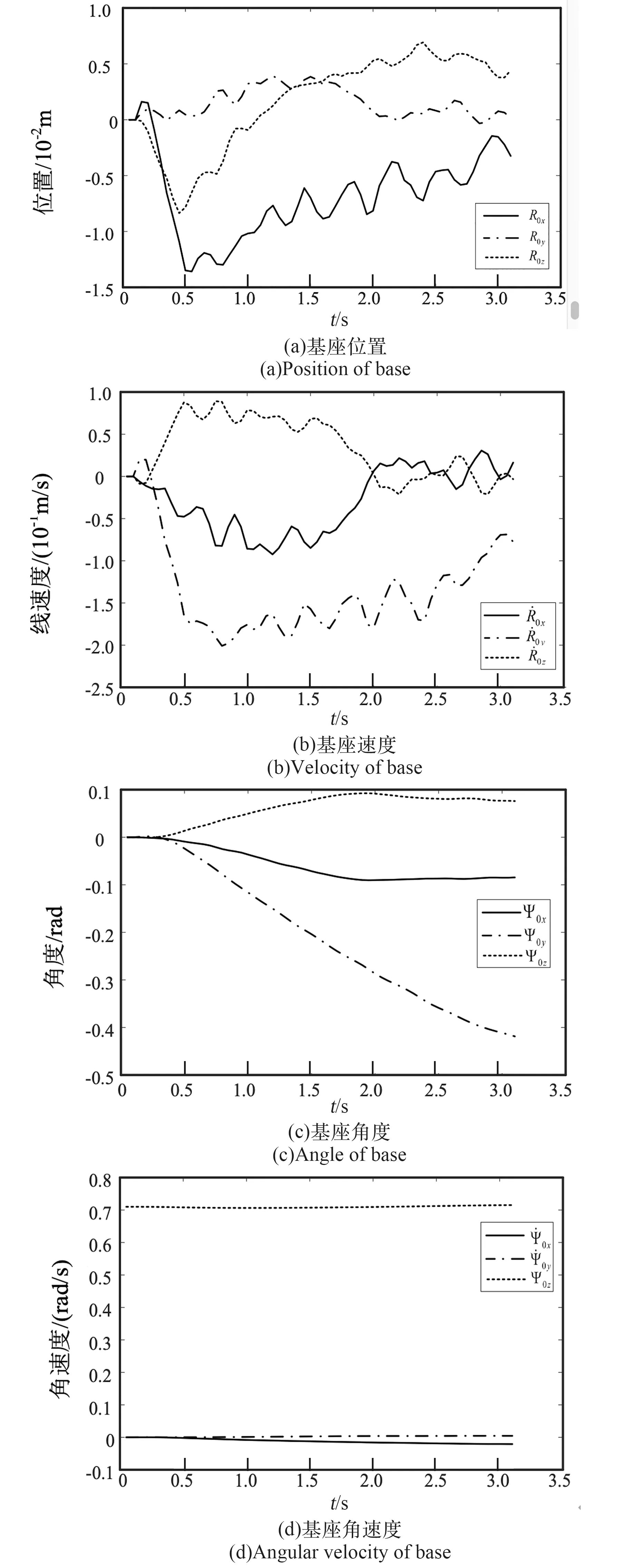
图9 漂浮基座位置、速度、角度及角速度曲线图Fig.9 Position, velocity, angle and angular velocity curves of free-floating base

由图5可知，抓捕机构从初始位置机动至抓捕位置时，关节角速度在抓捕初段逐渐增加，而在抓捕中后段逐渐趋于0附近，可有效降低空间机械臂与目标在抓捕瞬间的碰撞力；由图6可知，3个关节控制力矩在3 s以后逐渐收敛，且最终τxf值为0.1543 Nm，τyf值为0.4497 Nm，τzf值为0.4497 Nm，综合力矩‖τf‖为0.6615 Nm，满足抓捕条件中的关节输出力矩‖τt‖2≤1 Nm的指标要求，表明DDPG控制算法可实现抓捕末段减小与目标碰撞力的要求，更有利于捕获过程系统的姿态稳定；由图7和图8(a)可知，整个抓捕过程中，机械臂末端抓捕机构的中心与目标抓捕中心点的间距逐渐趋于0，具体εtx=3.8E-3 m，εty=2.62E-3 m，εtz=2.0E-2 m，对应的空间三维距离εt约为3.318E-2 m，小于抓捕域球半径SR，即目标处于可抓捕范围内；由图8(b)可知，接近目标抓捕位置时，相对速度趋于0，具体vtx=1.9E-3 m/s，vty=1.1E-3 m/s，vtz=2.0E-3 m/s，综合相对速度为‖vt‖=2.97E-3 m/s。由图9可知，FFSM系统的漂浮基座在整个抓捕过程中随着末端抓捕机构的速度降低，姿态和速度均处于可控状态。

综合仿真结果可知：抓捕时刻的关节驱动力矩为0.6615 Nm，抓捕中心误差为0.02 m，机械臂末端与目标间的相对抓捕速度小于3 mm/s；以上指标均能满足预设的抓捕条件，可有效减小抓捕碰撞力对本体星和目标运动状态的影响，使得抓捕任务安全可靠。