月面热环境对登月服影响的仿真分析
2020-02-01王海亮张万欣杨洪瑞
王海亮,张万欣,李 猛,尚 坤,杨洪瑞
(中国航天员科研训练中心人因工程重点实验室,北京 100094)
1 引言
登月服是航天员实施月面出舱活动必不可少的个体防护与作业保障的核心装备,相比于近地轨道出舱活动,月球探测中的热环境条件更为苛刻,对登月服的防护要求更高。
月面为高真空环境(大气压力为10-12~10-11Pa)[1],可忽略对流换热及月球大气对太阳辐射能的衰减作用,而且不存在大气层温室效应,太阳无法照射到的阴影区和夜间的月面红外辐射热量直接流向太空,导致月球表面昼夜温差极大,赤道地区月昼温度约为400 K,太阳无法照射到的阴影区和月夜的月面温度为90 K[2]。
此外,月面热环境受月球自转与公转影响,月球自转1周的时间恰好等于公转1周的时间,自转周期为29.53个地球日[3],昼夜时长约各15个地球日,月面处于连续长时间的高温月昼或低温月夜。
对于登月服在月面的热分析,吴清才[4]建立了航天员与月面环境之间的热交换数学模型,将登月服简化为垂直于月球表面的圆柱体,通过理论计算分析了登月服在月球表面的热平衡;寇翠翠等[5]将人体划分为15个节段,将登月服简化为包裹在人体外的同心圆环,编程计算了月面温度为90 K和400 K,人体代谢产热率为300 W和600 W情况下登月服的热调节性能;Martin[6]研究了航天服使用镀铝表面和特殊表面处理2种不同工艺时,在无冷源、中等代谢产热条件下不发生人体过热的月面活动允许暴露时长;Jones[7]通过航天服的热平衡方程,计算了在行星表面有太阳照射和无太阳照射条件下的航天服外热流及外表温度;Ochoa等[8]调研分析了月面环境热特性、人体代谢数据和航天服外热流情况,建立了随纬度和时间变化的月面温度计算模型,使用热综合分析系统(Thermal Synthesizer System,TSS)和热仿真软件(Systems Improved Numerical Data Analyzer,SINDA)分析了不同形式登月服辐射器在高温月面的散热能力;Hager等[9-10]基于MATLAB建立了月面热仿真模型TherMoS,包含陨石坑、巨石和斜坡等月面热环境,并以等外表面积的立方体模拟航天服,以一个热节点模拟人体,计算着服航天员在月球和火星上的不同负荷水平和纬度下的静态最小和最大热负荷,进一步建立了登月服模型V-Suit,分析了不同太阳高度下沿不同路径运动时登月服表面的瞬态热流。
上述文献中[4,6-7]为理论分析计算,给定月面温度,将登月服简化为立柱,缺点是使用简化的登月服模型无法分析各个部位之间的温度差异,且未考虑靴子与月面之间的热传导;文献[5,8-10]分别采用数值计算、集总参数法、MATLAB开发程序对登月服的不同热性能进行了分析,但缺乏全纬度、昼夜全周期整服热交换的系统分析及不同部位温度的差异分析。
本文为研究月面出舱活动过程中月面热环境对登月服的影响,对月面环境下登月服进行热分析,使用TMG热分析软件,建立了月面-登月服热仿真模型,月面模型可根据不同纬度、不同时刻太阳辐照差异自动计算月面温度,采用蒙特卡罗法计算登月服与月面的辐射换热。针对不同纬度与不同时刻,开展了登月服漏热量和不同部位温度分布的热仿真计算与分析,为登月服的热设计提供参考。
2 月面环境下登月服传热分析
通常情况下,月面出舱活动选择在月昼进行,此时月球表面的主要热源有太阳辐照、月面红外辐射、月面反照、地球红外辐射、地球反照[11],同时还需考虑月表与登月服靴底之间的热传导,由此得到登月服与月面环境之间的传热关系,如图1所示。

图1 登月服与环境热交换Fig.1 Heat exchange between lunar EVA suit and environment
登月服外表面热平衡方程,如式(1)所示:
QS+QIR,E+Qalbedo,E+Qalbedo,M+QIR,M+QC-QIR
=λA1(To-Ti)/δ
(1)
式中,QS为登月服吸收的太阳直接辐照热量;QIR,E为登月服吸收的地球红外辐射热量;Qalbedo,E为登月服吸收的地球反照热量;Qalbedo,M为登月服吸收的月面反照热量;QIR,M为登月服吸收的月面红外辐射热量;QC为登月服与月球接触部位的传导热量;QIR为登月服外表面辐射热量;λ为登月服壳体的导热系数,A1为登月服的外表面积,Ti、To分别为壳体的内外表面温度,δ为壳体厚度。
各部分热量分析如下:
1) 太阳辐照。登月服吸收的太阳辐照热量为式(2):
QS=α1×AS×S
(2)
式中,α1为登月服表面太阳吸收比,AS为登月服在太阳入射方向的投影面积,S为月面太阳常数。由于地月距离相对日地距离很小,近似认为日月距离等于日地距离,太阳常数[12]选取平均日地距离 (S=1367 W/m2)。
2) 地球红外辐射。月球表面离地球最近点吸收的地球热辐射最强,此处地球辐射热流密度如式(3)所示:
(3)
式中,qE是地球表面的平均辐射热流密度,RE是地球平均半径,L是地月距离。月球表面的地球辐射热流密度小于0.6 W/m2,可以忽略登月服吸收的地球红外辐射热量QIR,E[3]。
3) 地球反照。登月服吸收的地球反照热量Qalbedo,E比地球红外辐射更少[3],地月平均距离约为384 400 km,地球反照对登月服的影响可以忽略不计[2]。
4) 月面反照。月球表面太阳吸收比为0.93,反射率为0.07[13],具有高吸收低反射的特点,表面月尘发生漫反射,可忽略Qalbedo,M对登月服的影响。
5) 月面辐射。登月服吸收的月面辐射热量如式(4)所示:
(4)
式中,X1,2为登月服对月面的辐射角系数,ε1为登月服的表面发射率,ε2为月球的表面发射率,σ为斯蒂芬-波尔兹曼常数,TM为月面温度。
6) 月面热传导。登月服靴底与月面接触部位发生热传导,如图2所示。
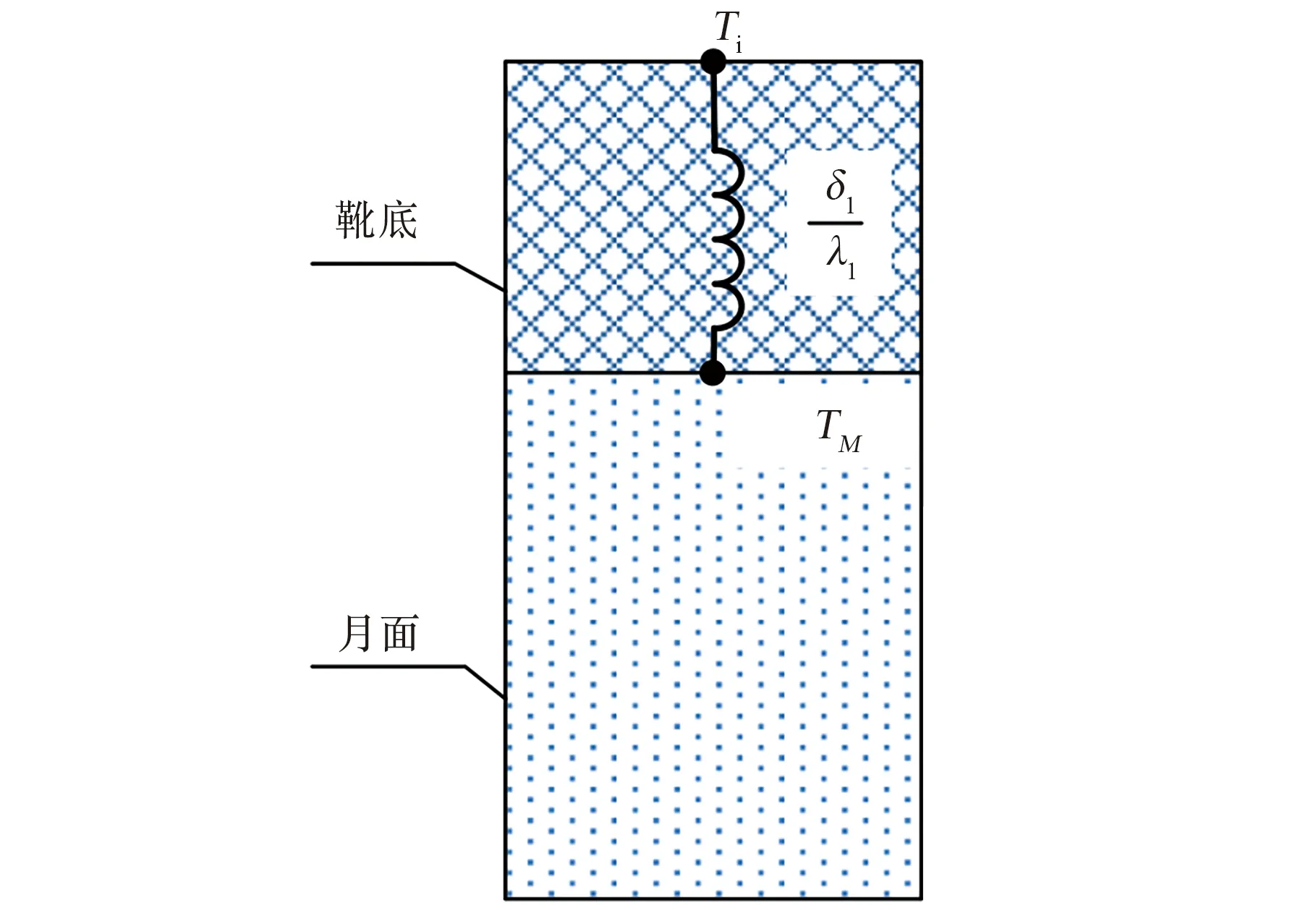
图2 登月服与月面的热传导Fig.2 Thermal conduction between lunar EVA suit and lunar surface
由于月面细小的月尘与靴底充分接触,忽略接触热阻,靴底与月面之间的传导热量如式(5)所示:
(5)
式中,TM、Ti分别为月表面、靴底内侧温度,δ1为靴底厚度,λ1为靴底导热系数,Acontact为靴底与月面接触面积。
7) 登月服表面辐射热量。登月服表面辐射热量如式(6)所示:
(6)
式中,ε1为登月服的表面发射率。
通过上述分析,地球辐射、地球反照和月面反照对登月服的影响可以忽略,登月服外表面的热平衡方程可简化为式(7):
QS+QIR,M+QC-QIR=λA1(To-Ti)/δ
(7)
在登月服内部还有人体代谢产热和设备产热,这些热量通过热控系统散热和漏热的方式排出。为研究月面热环境对登月服的影响,假设热控系统可以维持服内表面温度恒定,计算中以此为边界条件,不再对产热量和散热量进行详细分析。根据登月服外表面热平衡方程,建立登月服-月面的仿真分析模型,进而分析月面热环境对登月服的影响。
3 仿真模型建立
3.1 月面热模型
由于月壤的热扩散率很小,月壤一定深度下存在恒温层。徐向华等[3]通过数值计算得出1 m深处的温度波动不超过0.01 K,1.3 m深处温度波动幅度近似为0,可认为已经达到恒温层;Apollo-15任务报告[14]中记录,月球表面以下1 m深处温度恒定为250 K;Vasavada等[15]根据月球探测器LRO搭载的Diviner月球辐射计测量数据分析得出赤道地区0.4 m深处恒温为240 K;罗祖分等[16]计算出深度0.32 m处月壤温度为242.5 K,波动小于1 K。由于不同维度地区的太阳辐照不同,恒温层温度存在差异,徐向华等[3]、Butt等[17]、任德鹏等[18]对不同纬度的恒温层温度进行了计算,从纬度0°到90°,恒温层温度从230 K降到100 K。
根据上述分析,取月面恒温层深度为1 m,使用TMG软件建立厚度为1 m、尺寸为50 m×50 m的平板模拟平坦月面,平板顶部代表月球表面,平板底部代表月壤恒温层。表面划分三角形网格,沿厚度方向3D扫掠形成体网格,中心5 m×5 m区域进行网格加密,如图3所示。
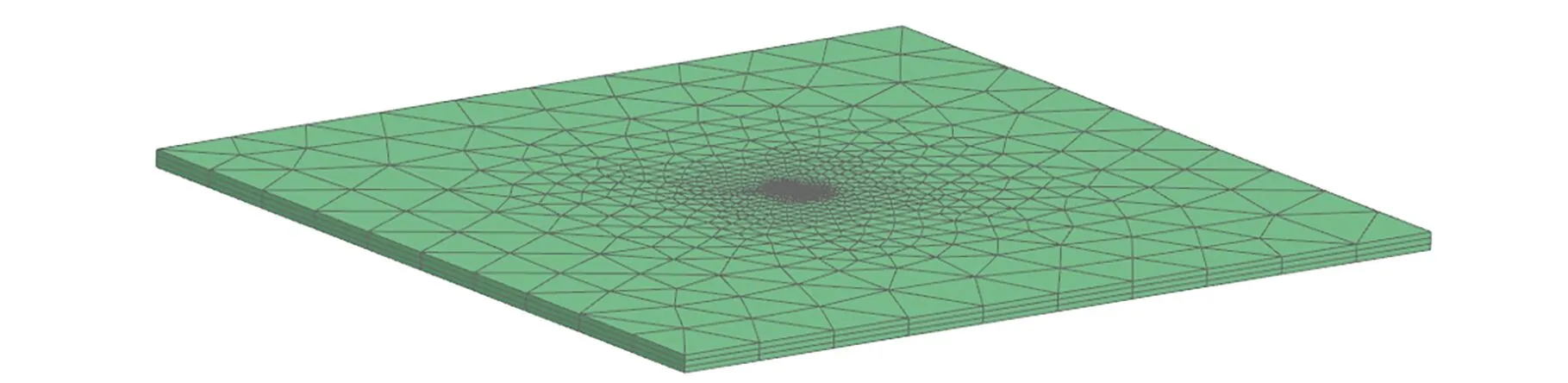
图3 月面热仿真模型Fig.3 Thermal model of lunar surface
月壤恒温层的温度按徐向华等[3]的结果计算,模型四周为绝热边界条件,太空环境温度取为4 K[19],月面热物性参数选取如表1所示,由月面模型可计算出月表面温度。

表1 月壤热物性参数[15,20-22]
3.2 月面-登月服热模型
登月服结构复杂,为了实现仿真模拟,对登月服进行如下简化假设:
1) 登月服表面各部位吸收比和发射率相同,参考典型航天服表面材料特性,发射率取ε1=0.75,吸收比取α1=0.4[22];
2) 登月服结构各部位导热系数相同,参照文献[23]中试验结果,取为λ/δ=0.25 W/(m2·K);
3) 服内表面温度均匀且恒温在299 K,不考虑其他服内产热。
登月服热模型包括头盔、躯干、生保背包、上肢、下肢、手套、靴子等,登月服站立于月面热模型中央,面向正北,如图4所示,模型使用四面体单元进行网格划分。

图4 月面-登月服热模型Fig.4 Thermal model of lunar surface-lunar EVA suit
3.3 计算工况
按前述分析选取的月面和登月服热物性参数、边界条件,计算在月面不同纬度、不同时间登月服受热情况,纬度和计算时间选择如下:
1) 纬度。为了分析登月服位于月面不同位置的受热差异,选择月球表面不同纬度地点,纬度分别为0°、20°、40°、60°、80°。
2) 计算时间。计算周期为一个月球日,即29.53个地球日。计算起始点为月面正午,计算终止点为次日月面正午。
4 热仿真计算
首先利用月面热模型,按计算工况进行计算,验证月面热模型的准确性,并分析月面温度分布特点,然后在此基础上,利用月面-登月服热模型计算登月服的温度分布与漏热量。
4.1 月面热仿真
文献[3]对月球表面热环境数值分析的结果在国内得到广泛认可,文献[15]根据高分辨率月球探测器Diviner的测量数据修正了月面温度模型。本文使用月面热模型计算得到赤道地区的月面温度,月面最低温度为101 K,最高温度为394 K。将计算结果与上述2份文献进行比对,见图5和表2。其中,本文计算的月面最高温最高,比文献[15]计算结果高11 K,月面最低温在二者之间,比文献[3]计算结果低11 K,比文献[15]结果高4 K。三者计算结果趋势一致,说明月面热仿真模型准确有效。
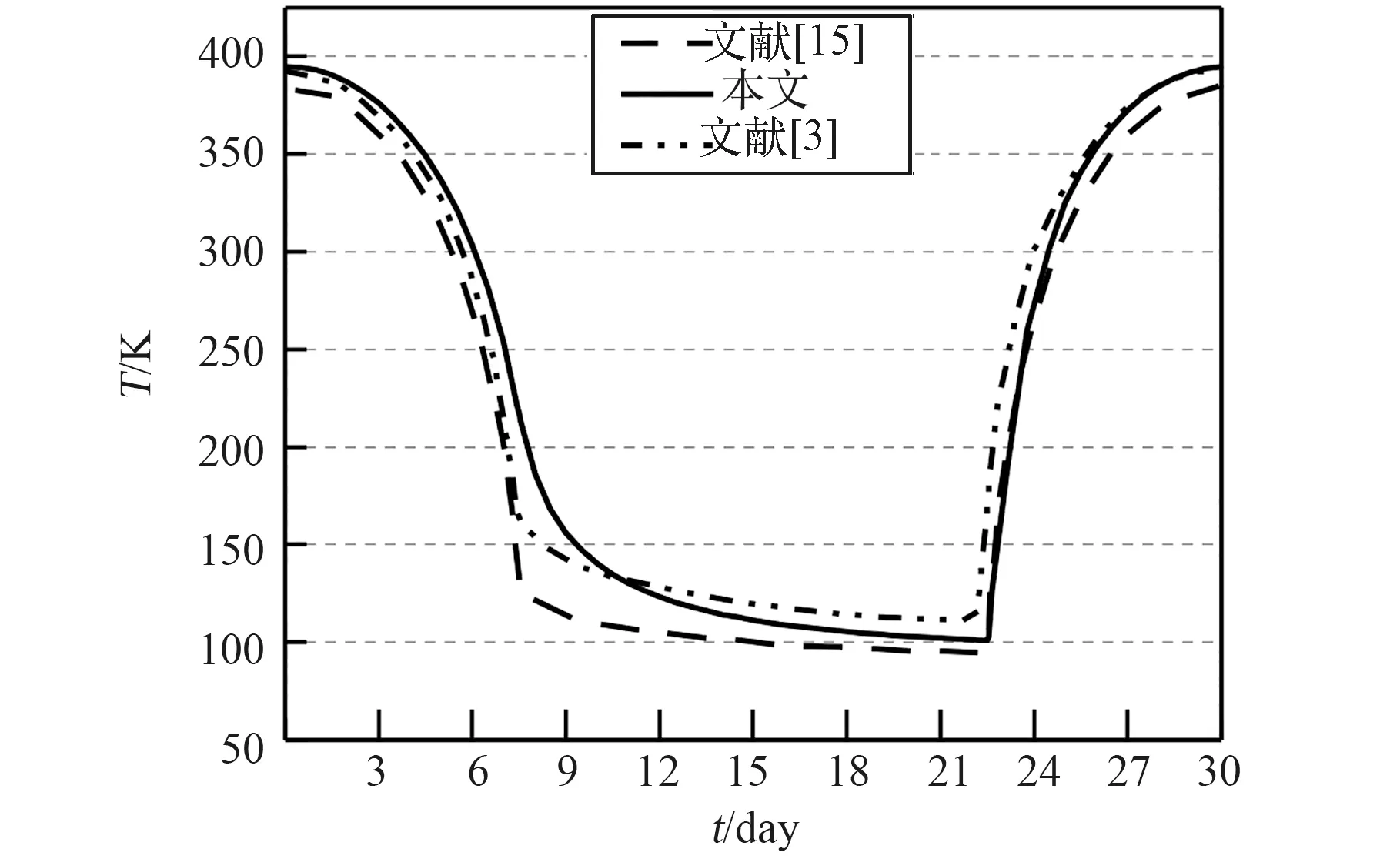
图5 赤道月面温度计算结果Fig.5 Calculated lunar equatorial surface temperatures

表2 赤道月面温度对比
按计算工况设定的纬度计算月面温度,计算结果如图6所示。
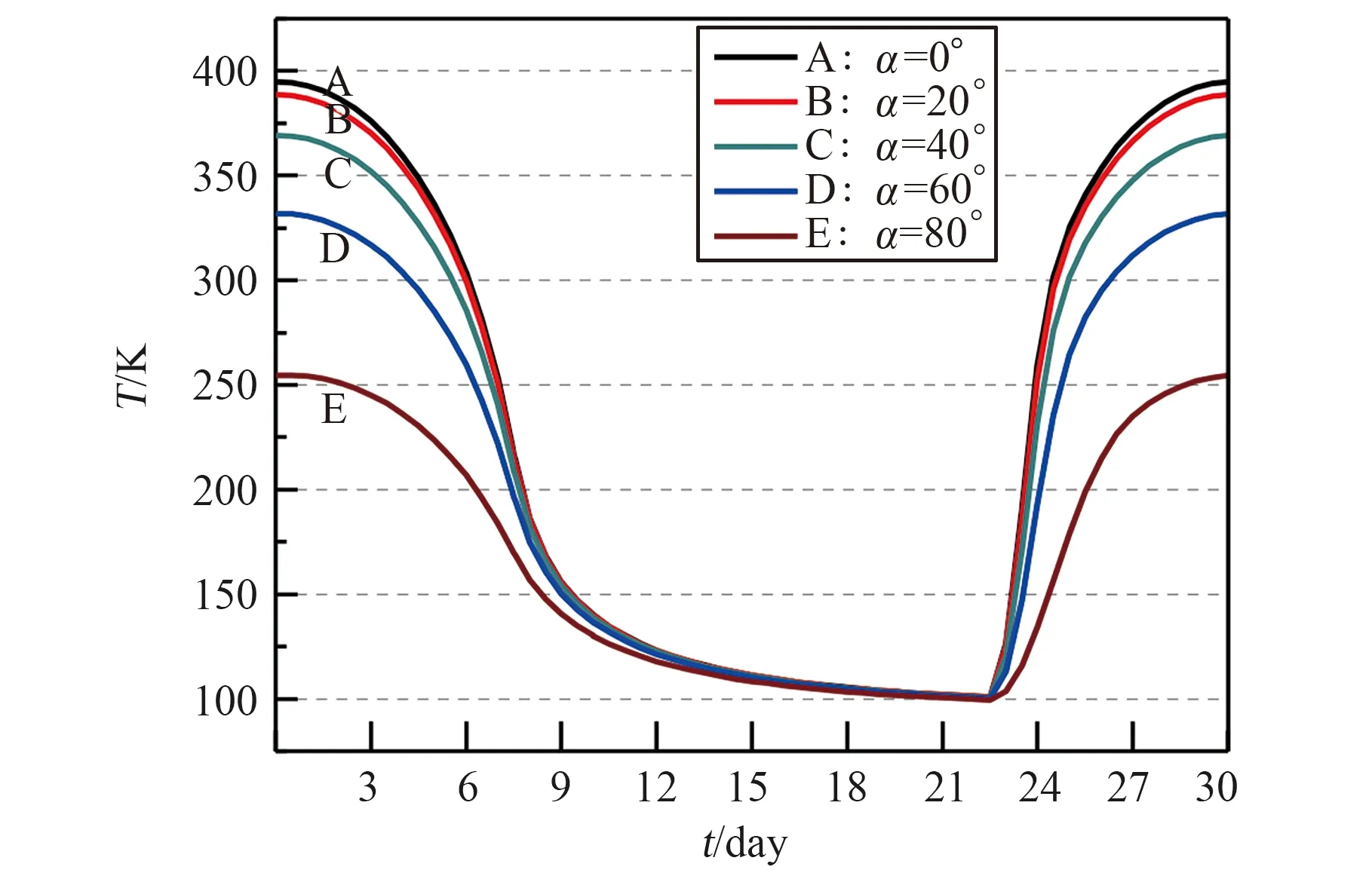
图6 月面温度仿真结果Fig.6 Simulation results of lunar surface temperature
图6可以看出月面温度分布特点如下:
1) 月球表面最高温度为394 K,位于赤道(纬度α=0°)正午,与航天器所处的月昼月面温度400 K接近[2],误差为6 K;
2) 月球表面最低温度为100 K,处于月夜或阴影区,无太阳辐照。月夜航天器所处的月面温度为90 K[2],误差为10 K;
3) 对比不同纬度地区,月午月面温度从纬度0°到纬度80°逐渐降低,且高纬度地区的温度梯度更大,月夜温差不明显,且波动较小;
4) 同一纬度,日落、日出过程温度变化率较大,且日落过程温度变化率小于日出过程温度变化率。
4.2 登月服温度分布
完成月面热模型验证后,利用月面-登月服热模型,计算登月服外表面的温度分布。不同纬度地区登月服外表面温度计算结果如图7所示,月午温度在270~327 K,月夜温度在170 K左右。

图7 登月服外表面温度Fig.7 External surface temperature of lunar EVA suit
选取纬度20°、太阳角度150°工况进行分析,此工况下太阳位于登月服右后侧,如图8所示,由于登月服遮挡太阳辐照,在月面形成阴影区,阴影区比周边月面温度低约200 K。

图8 登月服在月面的阴影 Fig.8 Shadow of lunar EVA suit on lunar surface
图9给出了上述工况下登月服前侧、后侧、左侧、右侧及背包顶部和底部的温度分布,可以看出:后侧温度高于前侧,右侧高于左侧,这与太阳位于登月服右后侧的实际情况相符;由于月面红外辐射的影响,背包底部温度明显高于背包顶部温度,该现象与文献[21]和文献[25]一致,朝向月面一侧吸收外热流最大;棱边、棱角容易出现温度极值点。

图9 各部位温度分布(纬度20°,太阳角度150°)Fig.9 Temperature distribution(latitude20°, solar angle150°)
进一步对登月服不同部位温度进行计算,包括脚部(feetl、feetr)、下肢(legl,legr)、上肢(arml,armr)、手部(hdl,hdr)、前侧(front)、后侧(back)、顶部(top)、底部(bottom)。极热工况(α=0°,noon)和极冷工况(α=0°,night)下,登月服各个部位的平均温度如图10所示。
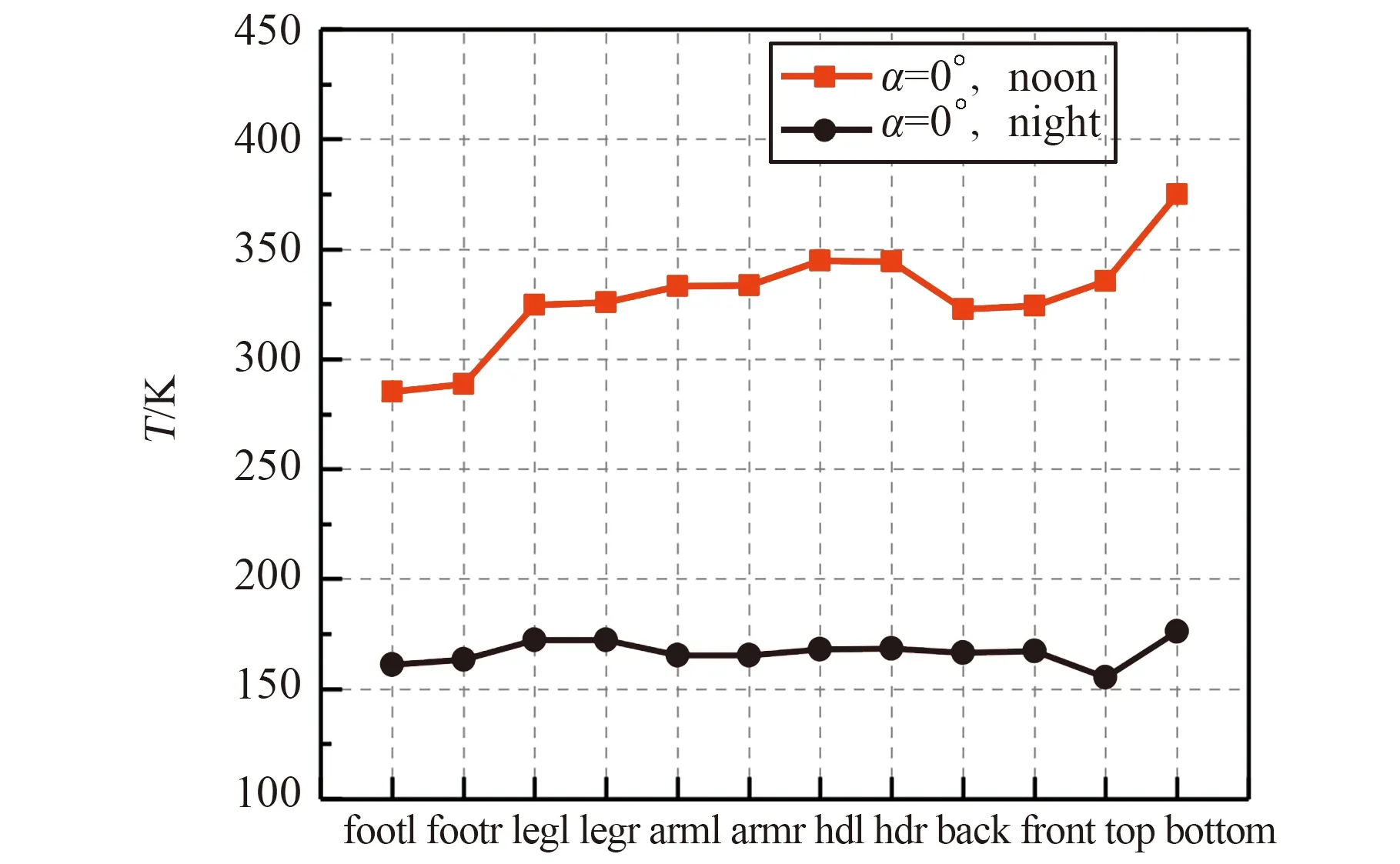
图10 登月服不同部位温度对比Fig.10 Comparison of temperature on different parts of lunar EVA suit
不同部位温度对比分析如下:
1) 极热工况下(α=0°,noon),各部位温差较大,温度范围为275~375 K;背包底部温度最高,由斯蒂芬-玻尔兹曼定律可知,该现象的原因是随着月面温度的上升,月面半球向总辐射力急剧增加,对背包底部有强烈的加热作用;背包顶部虽然受到太阳直射,但温度仍低于背包底部,表明月面高温辐射影响大于太阳辐照;包括靴子四周立面和顶部脚面的脚部温度最低,原因是脚面背对月面,且被登月服遮挡太阳辐照。
2) 极冷工况下(α=0°,night),各部位温差较小,温度范围为155~176 K;顶部温度最低,底部温度最高,主要由于顶部面向太空热沉,底部面对月面,月面温度高于太空热沉。极冷工况下各部位温差明显小于极热工况,主要是由于月夜月面温度为100 K、太空热沉为4 K,由斯蒂芬-玻尔兹曼定律可知,两者的半球向总辐射力相对登月服都很小,登月服与月面和太空环境面的热势差差异小,因此登月服各部位温度差异小。
4.3 登月服漏热量
登月服在不同纬度、不同时刻的漏热量计算结果如图11所示。

图11 登月服漏热Fig.11 Heat leakage of lunar EVA suit
从图11中可以看出:
1) 赤道正午,对应月面最高温度工况,漏入登月服热流量最大,漏入热量为39 W。
2) 月夜或阴影区,对应月面最低温度工况,漏出登月服热流最大,漏出热量为-105 W。
3) 出舱活动中,航天员处于走动状态,靴底月面的温度可假设为恒温,温度按图6 计算,由靴内侧温度和月表面温度根据式(5)计算靴底导热量。典型航天服靴底由2层4 mm厚的皮革夹衬真空绝热隔热层组成[22],皮革导热系数取0.03 W/(m·K)[26],真空屏蔽隔热层厚度和导热系数分别取为3 mm、0.005 W/(m·K)[24],则靴底的当量导热系数为0.012 W/(m·K),图12给出了赤道和纬度80°不同地点不同时刻的靴底导热量。赤道月午漏入热量最大为7 W,月夜漏出热量最大为-15.5 W。考虑靴底导热后,登月服最大漏入热量为46 W,最大漏出热量约为-121 W。
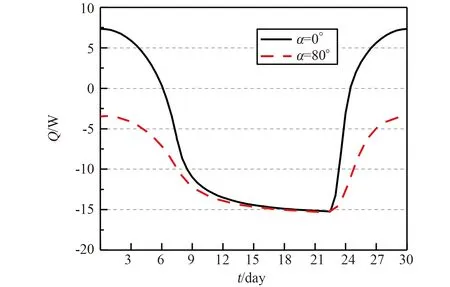
图12 靴底导热量Fig.12 Heat conduction through boot soles
4.4 登月服热设计建议
根据上述计算结果与分析,为登月服热设计提出以下建议:
1) 为降低月昼的热控系统负荷,可进一步提高结构的隔热性能、降低外表面的吸收发射比,以减少热量漏入;
2) 由于月昼月面温度较高,月面红外辐射对背包底部等对月面有强烈的加热作用,应提高这些部位的热防护;
3) 登月服在月面形成的阴影区,温度比周边低约200 K,在登月服热防护设计中可以考虑利用该阴影效应为登月服遮阳;
4) 登月服靴子与极高低温的月面接触,需要加强靴底部位的隔热性能;
5) 由于结构的棱边、棱角处热容较小,会出现温度的极值点,结构设计时应避免棱边、棱角等。手部与手指处厚度较薄,也会出现温度极值点,应加强热防护。
5 结论
1) 月昼时,登月服对月面受到强烈的月面红外辐射加热,各部位温差较大,且靴底会与394 K的高温月面接触;
2) 相比月昼,月夜登月服表面各部位温度差异较小,但登月服靴底会与100 K的低温月面接触;
3) 登月服漏热量和外表面温度随纬度和时间变化,漏热量变化范围为-121~46 W,月午外表面温度范围为270~327 K,月夜外表面温度在170 K左右。
如上所述,月面出舱活动中登月服将处于极高低温的月面环境,受到强烈的月面红外辐射,并与极高、低温的月面接触。登月服热设计中需要针对这些问题,提高被动热防护能力,减少漏热量,并加强靴底、对月面等部位的局部热防护。
