让复习课不再流于形式

杨利容

[摘要]复习课应尽可能地有针对性，集中处理学生易混淆的知识点，帮助学生攻克学习的重难点，构筑知识框架，实现切实有效的复习。

[关键词]复习;学情;混淆点;易混点;知识面

[中图分类号]G623.5

[文献标识码]A

[文章编号]1007-9068（2020）32-0066-02

及时复习是提升教学质量的必要手段，同时也是学生巩固深化认知结构、提高学习能力的重要途径。目前教材编排的复习课过于求全，教师往往采用做题的方式来引导学生复习巩固，这种炒旧饭的做法让学生兴味索然。复习课要起作用，拿捏住复习精要是关键。对此，笔者归结出以下几点经验。

一、结合学情，辨析对比，集中处理混淆点

复习课一般以单元为节点，有时也可以打破成规，根据学情自行安排。复习课不妨迎难而上，专挑险隘进攻，集中处理知识的混淆点。

[案例1]三年级“长方形、正方形周长与面积”的复习。

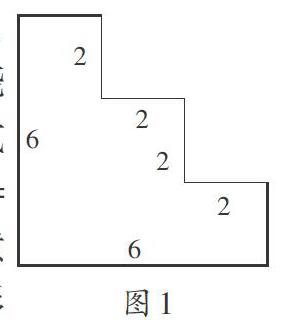
周长与面积的几何概念分属三年级上下两学期。学完面积后，很多学生会将周长与面积混为一谈，张冠李戴。笔者认为“长方形、正方形的周长与面积的复习课”可将教学重心放在整理上，深化二者的意义分辨。例如，围绕“6×4=24”“4×4+2×2=20”这两个算式进行复习，可先出示算式一“6×4=24”，再让学生根据算式画几何示意图，利用平移思想求出不规则图形周长，并比较变形前后的周长与面积。教师出示图1，并提问：“它的周长也能用6×4=24（厘米）计算吗？求它的周长与面积。”再出示算式二“4×4+2×2=20”，从周长、面积两个方面去理解并画图。

笔者以乘法算式“6×4=24”为思维辐射源，让学生展开想象去尽情表示不同图形的周长或面积，并在方格纸上作图。学生有的画出长6厘米、宽4厘米的长方形，有的画出边长为6厘米的正方形，有的则心思缜密，将所有可能的矩形全部画出，甚至个别特优生还运用平移思想，画出了不规则几何图形。接着，教师设问：“这个算式，何时表示周长，何时表示面积？”示意学生关注量词的运用，严格区分长度与面积的度量单位，突破知识难点，也借此机会辨别长度和面积概念;再以此算式为核心，推广到将不规则图形平移求周长上，进一步强化周长与面积的差异;最后让学生根据算式“4×4+2×2”作圖，加深对面积和周长的定义的理解。一个平常的算式将周长与面积的区别揭示得淋漓尽致，从算式到图形的转变增强了学生的空间观念。算式生动诠释了周长与面积的定义，无声的解说释放出巨大的导学能量。

观点简述：复习课不是录像回放，制定复习课内容时，教师可结合学情精简内容、巧妙装配，如将平均数、中位数、众数等统计概念组装起来进行复习，也可将所有倍数问题整合在一起复习。选择易混淆的知识点进行辨析对比式复习，不仅可让学生辨明真相，还可使学生搭建起逻辑清晰的认知结构，为将来的学习奠基。

二、以旧换新，变练习为钻研，攻克重难点

对于学生的易错点，一般处理模式为布置练习，通过练习试错，让学生形成免疫力，提高识别错误的能力，若一次无效则加大练习量，直到学生形成敏感的防错心理机制，但这样做往往事倍功半。其实在复习课中，这些顽固的易错点也可反转成为有利的教学资源。

[案例2]二年级“有余数除法”的复习。

笔者曾听过一节“有余数除法”的复习课，授课教师别出心裁围绕难点设置通关环节，令人印象深刻，深受启发。第一关：速算。列式计算22÷8，34÷4，28÷5，52÷7。如何检验答案的正误？先要判断余数是否大于除数，再用“商×除数+余数=被除数”来检验。第二关：灵活运用。问题1：有37条花边，每条裙子要缝上5条，可以缝制几条裙子？问题2：有37千克汽油，每个油箱能盛下5千克，需要几个油箱？学生先独自思考，再交流汇报。举例：在生活中像装汽油这样，结果需要额外加1的情形多吗？用事实说话。第三关：寻找“吉祥数”。隐去“百数表”中的部分数字，寻找“吉祥数”，成为“吉祥数”的条件：□÷9后所得的余数是8。学生先独立计算，再逐个圈点出“吉祥数”;查验找到的“吉祥数”是否有误;观看屏幕，试着找出规律。

这节复习课没有在解决普通余数问题上浪费时间，而是集中精力攻克难点，直击要害：所求的商数是否需要额外加1，余数与除数孰大孰小。教师将这些难点列为“攻关对象”，让学生通过比照、列举等形式进行深入解剖。

观点简述：学习重难点的攻破绝非易事，复习课上让“老面孔”换上“新装”，可激起学生主动探究的动机，让学生更深刻地认识问题，并以此为联络点，编织一张严密的知识网络。特别是在第一学段，复习的内容少，要求偏低，机械重复式复习只会降低学习趣味。在复习课中，摘选难点体现的不仅是模式的转变，更是思想的更新。

三、构筑框架，编制网络，铺满知识面

复习课需要引导学生构建起知识网络，以促使学生形成科学、高级的认知方式，这是复习课的重大功能，第二学段的复习尤其如此。这种做法极具挑战性，需要教师高瞻远瞩，不断凸显核心知识的学习，才能引领学生不断进步。

[案例3]四年级“图形的认识”的复习。

每一类图形的学习虽各具特色，各有侧重，但图形的认识具有共性，如果可以牢牢抓住它们之间的关联，对于学生整体把握图形特征、形成平面几何观念将起到醍醐灌顶的作用。

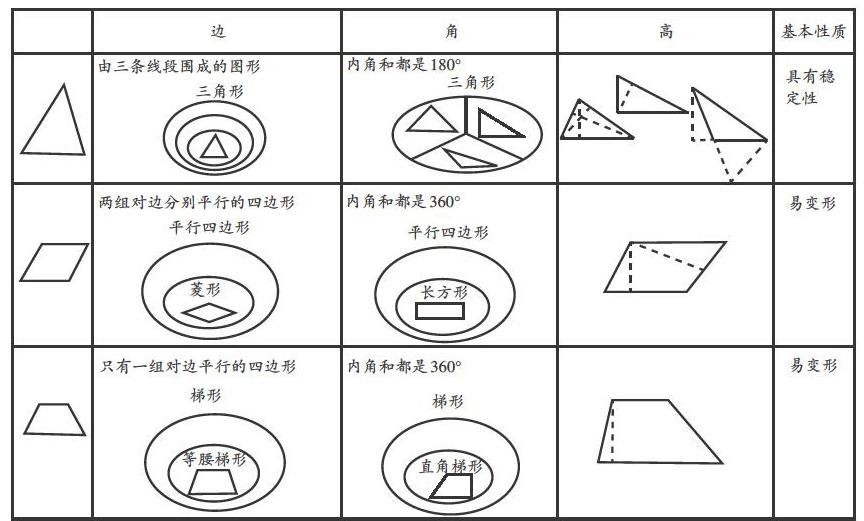
下图是“图形的认识”复习课所构建的主要认知网络：

教师以复习三角形为示范，围绕边、角、高、基本性质整理出认识三角形的基本方式，然后让学生仿照这个模板，对平行四边形和梯形进行复习。反馈时，师生共同整理，构建起认识平面图形的基本通则。这样的认识方式有利于举一反三，可应用到其他知识的学习中。

观点简述：教师不妨多开展类似的复习课，例如体的认识、数的认识、数的运算等，除了整理教学内容，还可以命制具有相同数学思想的专项训练题，以帮助学生集中掌握某一数学思想，如转化思想、数形结合思想等。

在研究大量的复习课教学后，笔者总结出了上述复习精要，符合基本的教学规律，更符合新课标的主旨。复习内容越是科学合理，复习效果就会越明显。

（责编 罗艳）