优化课堂教学 发展创新思维

王玲

[摘要]在小学数学教学中培养学生的创新意识与能力十分重要。在日常的数学教学实践中，可以通过激发学生的想象力、引导学生多角度进行思考、保护学生的好奇心等途径，为学生营造有利于发展创新思维的课堂氛围，让学生能积极主动地参与知识的发现，亲身体验数学创造的过程，从而发展和培养学生的创新思维和创造才能。

[关键词]创新思维;想象力;好奇心

[中图分类号]G623.5

[文献标识码]A

[文章编号]1007-9068（2020）32-0054-02

习近平主席曾这样说过：“创新是一个民族进步的灵魂，是一个国家兴旺发达的不竭动力，也是中华民族最深沉的民族禀赋。”一位教育专家说：“培养学生的创新能力，比教会他知识更重要。只有让孩子学会独立解决问题，才能让他们走得更远。”作为一名数学教师，应注重用科学的方法培养学生的创新思维和创新能力。

荷兰数学教育家弗赖登塔尔认为现实中存在两种数学：一种是现成的或已经完成的数学，另一种是活动或创新的数学。数学教师在把握时代脉搏的同时，还应顺应教育改革的方向，在日常的教学实践中为学生营造有利于发展创新思维的课堂氛围，让学生能积极主动地参与知识的发现，亲身体验数学创造的过程，从而发展和培养学生的创新思维和多方面的创造才能。在小学数学教学中，笔者尝试通过以下几个方面来培养学生的创新思维。

一、安排动手操作，重视学生获取知识的思维过程，发展学生的创新思维

在小学数学教学中，教师要结合教学内容，遵循学生的认知规律，积极安排学生动手操作，重视学生获取知识的思维过程，从而发展学生的创新思维。

例如，在教学“认识平均分”一课时，教师利用故事引入，并提出问题：“把6个桃子分成两堆，可以怎样分？”学生用6根小棒代表6个桃，自己动手尝试分，再说一说是怎样分的。教师根据学生的回答按每份个数相同和不同把这些分法分成了两类，借机引出“平均分”的概念：每份分得同样多叫作平均分。接着加深学生对平均分的认识，引导学生思考：这6个桃还可以怎样平均分呢？学生同桌讨论，然后用小棒摆出自己的分法，随后说一说为什么摆出不同结果（每份1个、每份2个）的分法也是平均分。至此，学生对平均分的理解水到渠成。这时，教师再次强调：把一些物体分成几份，只要每份分得同样多，就是平均分。这是学生从实际操作中真切体验到平均分可以按每几个一份地分，所得的结果是能看出分成几份，从中获得分法的直接经验。紧接着，教师再次让学生把8根小棒按“每（ ）个一份，分成了（ ）份的分法”说一说平均分是怎么分的。这里通过学生的“说”逐步把具体操作的动作过程抽象成一种分法，学生在头脑里初步形成这种分法的表象，从而获得分法特征的初步体验。

作为教师，应给学生提供广阔的空间和适宜的土壤，进而培养他们的创新意识和创新思维。

二、激发学生的想象力，发展学生的创新思维

随着教育教学改革的不断深入，教育教学理念层出不穷，而研究我们的课堂，研究我们的学生，却是永恒的话题。正如顾志能老师所说：“提升教学效果，让教师教得更有味，学生学得更有效，是我们进行教学创新最根本的出发点和立足点！”课堂教学中，激发学生的想象力，也是发展学生创新思维与能力的重要支撑。

例如，顾志能老师在教学“长方体的认识”一课时，并没有让学生依托手中的长方体实物，通过看、摸、数等活动，对长方体的面、棱、顶点依次进行研究，得出三者各自的特征。他认为“长方体的认识”是学生第一次正式学习立体图形，发展空间观念是这节课的核心内涵。就数学教学理论而言，观察、操作、想象等是发展空间观念的有效手段，但是利用想象发展学生的空间观念，将会为学生的创新思维和创造能力的发展提供有效支撑。顾老师在让学生展示所带的长方体的盒子进行交流后，直接导人新课，在学生知道长方体有六个面的基本特征后，出示一张长是3分米，宽是2分米的长方形的纸，提出问题：“要围成一个长方体，还缺几个面？你能想象出另外五个面分别是怎样的长方形吗？”给学生充分的思考时间，引导学生观察手中的纸片并想象，然后组织学生合作探究，根据学生的描述，借助课件，让学生在头脑中逐步建立起长方体六个面的清晰表象。顾老师以“给定一个面，想另五个面”为载体，引导学生想象，让学生系统经历了从一个面到六个面的组建过程，从而深刻理解了面与面之间的联系，体会了棱的形成以及棱与面之间的关系。这时学生收获的不仅仅是“长方体有六个面，六个面都是长方形，相对的面完全相同”这样简单的结论，更重要的是在顾老师深入挖掘教材下學生的空间观念得到发展，创新意识和能力的生成得到促进。

三、多角度进行思考，优化学生解题能力，发展学生创新思维

数学的发现和创造来自于不断地探索中产生的灵感。当学生从不同角度、不同方面去思考解决问题的方法，亲身经历参与解题的过程，感受到数学技能、方法是有章可循的，并非一成不变时，学生就会思维敏捷活跃，学习效率高，这就是发展学生创新思维及创新能力的最好时机。

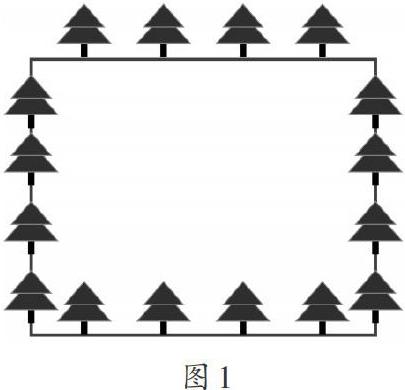
例如，二年级上册的练习中有这样一题：“把16棵树种在一个正方形地的边上，要使每条边上的棵数相等，可以怎样种植？请画出示意图。”大部分学生会根据正方形四条边长度都相等的特点，把16棵数平均分成4份，那么正方形地每条边上就可以种植4棵树。（如图1）

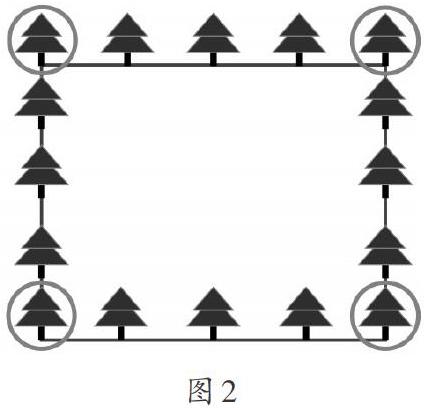
这时教师提出问题：“仔细思考一下，是否还有其他种植方法？”（给学生留有思考的空间）当问题抛出后，有几位学生的小手高高举起，教师当即让一名学生上台边讲解自己的思路，边在黑板上画出简单的示意图（如图2）。

此时，台下响起了热烈的掌声，学生也发表自己的看法：“哦，原来可以这样，我终于明白了。”“哎呀，我刚开始也是这么想的，但我没有继续深入思考。”……与众不同的意见体现了思维的独特性，说明学生把握住了事物的本质及核心。著名数学家波利亚说过：“掌握数学就意味着要善于解题，善于解题就必须设计解题思路。”善于解题，设计解题思路就是要多角度地思考，优化解题能力，从而发展学生的创新思维，提升学生的创新能力。