阻断思维定式，让迁移由“负”转“正”

张晓霞

[摘要]虽然学生的错误资源往往可以成为重构知识的契机，但是错误可以形成免疫，也可以带来偏执。因此，面对一些有可能形成思维定式的“坑洞”，必须追根溯源，从知识的来历讲起，重组知识结构，帮助学生辨明知识生成的始末，切实提升教学效率。

[关键词]近似数;十万位;万位;保留数位;取值

[中图分类号]G623.5

[文献标识码]A

[文章编号]1007-9068（2020）32-0034-02

偶然的机会，读到一篇教研论文，题目为《着急的明理，草率的回归》（以下简称文1），针对发表在同一期刊上的另一篇论文《惑于始，解于端》中提及的一道练习题发表论述，而这道题又是出自另一篇论文《是什么、为什么、怎么办》的论点，三篇高质量的论文跨时空论战，各有千秋。

对于文1中的观点和处理策略，笔者深表赞同。在实际教学中，笔者曾出示一道同类题：某整数取近似值是10万，请你推测出原数的可能范围。被调查的80名学生中，竟然有50人不约而同地填写“95000～104999”，只有5人填写“50000～149999”，余下是其他答案。

一、追查错因

这道题之所以难倒一批学生，究其原因，其一是学生受到类似“把一个整数保留到万位后取值10万”题型的误导，后面遇到的所有练习题都下意识地参照此解题过程，因而得出“95000～104999”的答案;其二是多数学生陷入经验陷阱，看到大写的“万”字，就想当然地以为这个整数是保留到“万”位，遵从“四舍五入”法，那就需要审查千位上的数字来判断究竟是该“四舍”还是“五入”;其三是有些学生认为“有一个整数，把它保留到万位后是10万……”和“有一个整数，把它保留数位后是10万……”两种表述大意相同，实则理解有误;其四是教师的教学存在缺漏，多数学生对这部分知识是“一题一得，一事一议”，生搬硬套，没有做到融会贯通、举一反三。尤其是出现这种需要反向推理的题型时，学生理解起来更加困难;其五是出题人超前出题。课程标准明确指出：会用万、亿为单位表示大数。按照课程标准的指示，并未刻意避开“单位”的近似数这一提法，人为提高准入门槛。笔者还查了本册教材制订的所有教学目标，可以确定这样一个总目标：使学生学会用“四舍五入”法省略小于一亿的数万位之后的尾数，来求近似值。

二、追根溯源

1.爭辩

笔者出示原题：

1.某整数，保留数位后取近似值是10万，这个数的原值范围上限是（ ），下限是（ ）。

2.某整数，保留到万位后取近似值是10万，这个数的原值范围上限是（ ），下限是（ ）。

师：上面两道题有区别吗？

生1：有，一个明确规定要保留到万位，一个则没有作此规定。

生2：第1题尽管没有注明要保留到万位，但10后面连缀了一个“万”字，暗示要保留到万位。

生3：我不同意生。的说法，“10万”只能代表取近似值后的数值。

2.感悟

于是，笔者将“10万”写在黑板上。

师：“10万”去掉单位万，改写成阿拉伯数字是什么？

生4：100000。

生5：删除“万”字，再添补4个0即可。

师：照这样，“某整数，保留数位后取近似值是10万”是否等价于“某整数，保留数位后取近似值是100000”？

生6：等价。

师：好，按照这种逻辑，那“某整数，保留数位后取近似值是100000”，没有了“万”字，谁来说一说，你觉得这个近似值保留到了哪一位？

生7：十万位，因为这个数的最高位是十万位。

生8：从万位开始都是0。根据“四舍五入”法可知，当万位上的数小于等于4时，则将万位上的数字舍去;当万位上的数大于等于5时，则先向前进位后再归零。无论万位上的0是什么来历，总之必须清零。于是推知，是将原数保留到了十万位。

师：保留到十万位，主要取决于哪一位上的数字？

生9：万位。

师：检索最大值时，万位上的数字可能出现哪些情况？

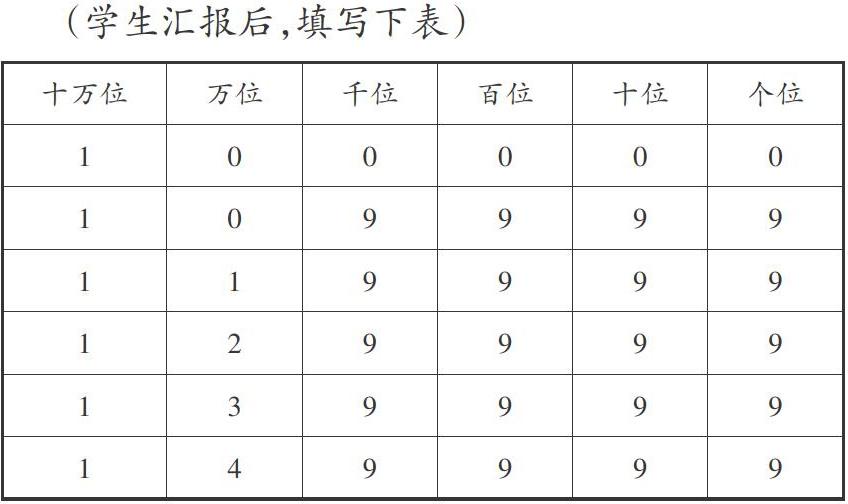
师：那么万位后面的数字怎么设置呢？可以设想哪些数？

（学生汇报后，填写下表）

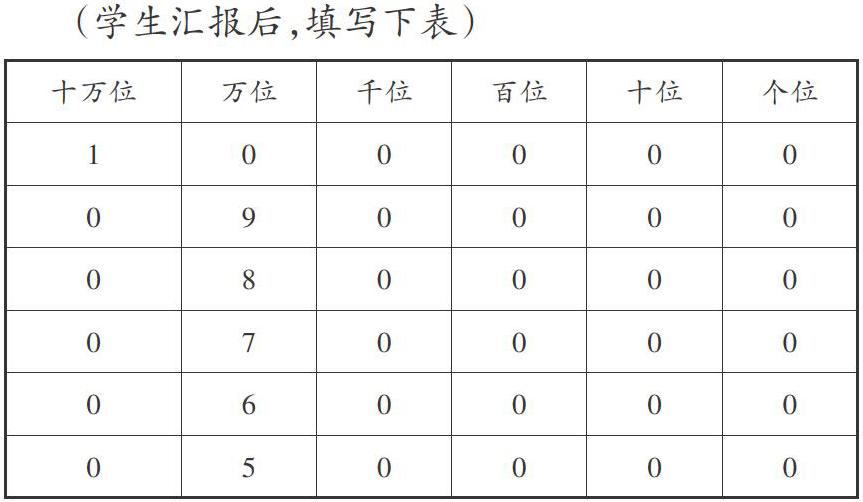
师：检索最小值时，万位上的数字存在哪些情况？这时，万位之后的各位上怎么设置数字？

（学生汇报后，填写下表）

3.明理

师：“某整数，保留数位后是10万，请你写出它的取值范围”，应该怎么设想呢？

生10：大于50000，小于149999。

生11：不对，正确答案应是大于或等于50000，小于或等于149999。

师：如果用x表示这个数，那么可以用不等式表示取值范围为50000≤x≤149999。

师：请大家细致观察以上表格，依照这种思路，谁能叙述一下操作方法？

生12：看表可知，保留到十万位后的近似数是10万，检索最大值时，实际值超过十万，用的是“四舍”法，万位上最大可取值4，其余数位最大均可取值9。

生13：看表可知，保留到十万位是10万，检索最小值时，十万位上的数字可以为0，即十万位缺位，原数小于10万，此时采用的是“五入”法，万位上的数必须大于5，由于是最小值，因此万位上最小可取值5，其余数位最小均可取值0。

生14：我发现十万位上的数字有规律，检索最大值时维持原状不变，检索最小值时则要减1。

生15：我发现表格中万位上的数字也有规律，纵向看恰好是0～9，合计10个数字。检索最大值时取4，检索最小值时取5。

生16：看题目有无明确提出保留到哪一位，具体情况具体分析。

师：好一个“具体情况具体分析”。遇到这类题目时切不可操之过急，一定要沉着冷静，关键是分清这个近似数是保留到了哪一位，这才是正确解题的法宝。其次我们可以利用表格来解题。

三、课后反思

对待每一节课，教师都要“三思”：第一思，你要把学生引向何处？第二思，你采用什么引路方式？第三思，你如何确认已经达到目的？

“把学生引向何处？”——笔者对学生的经验和学情严重误判，主观臆测成分偏多，没能统筹兼顾到全体学生，在顶层设计上无法做到在基本层面上施策，只是片面强调了“四舍五入”法的取值法则。“采用什么引路方式？”——对于给出一个近似数检索出原数的取值范围的题型，笔者没有充分考虑到需要逆向思维才能解答的题型特征，没能搭设好催化逆向思维的知识链条，导致学生自主探究和反思时欲速不达，教学手段和策略无法施行到位，大大降低了学习效果。“如何确认已经达到目的？”——笔者只是“就题论题”，没有举一反三。

平素教学时，我们只将“四舍五入”法教给学生，这种程式化的操作自带了一些基本要件，那就是必须明确告知保留到哪一位数字。如，整数297800，精确到万位，结果是300000;改写成以“万”作单位的数，结果是30万;精确到十万位，结果是300000;改写成以“十万”作单位的数，结果仍是30万，保留结果和改写结果竟然毫无区别。改写单位时，如果精确到哪一位就以哪一位作单位的话也好区分，如300000（精确到万位）就写成“30万”，300000（精确到十万位）就写成“3十万”，但是，计数单位一般只有“万”“亿”等，所以没有“3十万”这种改写法，于是在没有指明精确度的逆向推导时，就会产生歧义。因此，对于上文中的例题，还原成阿拉伯数字更便于观察，可以作两种理解，然后取最大范围，因为95000到104999这个区间包含于50000到149999这个区间，所以正确答案应该是50000到149999之间。

基于以上认识，在学生充分辩论、探析后，为了确认已经达到目的，笔者又增设了应用、提示和拓展三个层级的巩固练习。通过以上改进举措，学生对这一知识点达到纯熟的程度。

（责编 李琪琦）