算法多样化到优化的教学改进

段晓炜 伍春兰

[摘要]以“两位数乘两位数”竖式笔算第一课时为例，针对两次实践与反思，从四个方面对小学数学计算教学提出四点建议：问题情境的选择、算法多样化到优化、算法与算理相随、学生调研的价值。

[关键词]两位数乘两位数;竖式笔算;算法多样化;数感

[中图分类号]G623.5

[文献标识码]A

[文章编号]1007-9068（2020）32-0031-03

算理和算法多样化、数感等已成为小学数学计算教学关注的高频词，但在教学中，教师往往顾此失彼，比如，放手让学生算法多样化，可学生并没有在比较中掌握需要学习的算法;又如，算理占据了一堂计算教学课的绝大部分时间，以至于最后的算法教学草草收尾。算法、算理如何权衡？数感怎样渗透？下面结合“两位数乘两位数的竖式笔算”第一课时，阐述我们的实践与思考。

一、三本教材相关内容概述

“两位数乘两位数的竖式笔算”这个内容，北京出版社（以下简称京版）教材、人民教育出版社（以下简称人教版）教材及北京师范大学出版社（以下简称北师大版）教材都将其安排在三年级下册，见表1。

三个版本教材所给情境不一，但都是 先考虑不进位的两位数乘两位数的笔算，抽取的乘法算式第二个因数也都不约而同地选择了12。12是具有六个因数的较小的两位数，既满足了算法多样化的条件，也降低了计算的难度（不进位乘法）。第一个因数，京版选择的是24，相比另两个版本教材选择的14，如果在点子图中标注，24就会过于“肿胀”。三个版本教材的转化算法2是沟通脱式计算与竖式计算的桥梁。另外，北师大版教材还多了转化算法3，即将两个因数都拆分为10和一位数的五步脱式计算方法。

对于竖式笔算，京版教材更强调步骤，人教版教材更突出算理，北师大版教材更注重数形结合。

二、第一次设计及实践

本次设计分为四个环节——情境引入、尝试转化、理解竖式、“铺地锦”激趣，旨在让学生通过算法多样化体验转化思想方法，在算法与算理的联系中理解竖式笔算。

【实践片段1】

1.转化解决问题

出示情境图1，提出数学问题：参加三年级花毽表演一共有多少人？让学生想办法将这个问题转化成之前学习过的知识，并借助点子图圈一圈，以留下思维过程，同时把思考过程用算式写下来。

由于给了较充足的时间，学生经过小组交流都得到了5种算法：14×2=28，28×6=168;14×6=84，84×2=168;14×3=42，42×4=168;14×4=56，56×3=168;14×2=28，14×10=140，28+140=168。

在众多算法中，让学生选择自己喜欢的算法，对应点子图圈一圈、说一说理由。算法多样化的背后是学生对于数与式理解的不断深入，不同的算法能够调动学生更多的对于数与式的感觉。在数（算式、结果）与形（点子图）的交互中，学生经历了抽象与具体等思维活动，数感和运算能力得到了强化。

2.理解竖式笔算

设计了2个活动：

由于学生之前学习过多位数乘一位数的竖式笔算，所以活动1的竖式笔算比较顺利。但活动2的竖式笔算，多数学生没有思路，所以教师提供了竖式，讓学生在此基础上理解算理并简化。

【实践反思1】

本设计原设想通过算法多样化，不仅引出两位数乘两位数的竖式笔算问题，而且发展学生的数感和化归意识。

事实上，学生沉浸在算法多样化中，以为问题都已解决了，可发现新的学习内容才刚刚开始，而此时课堂时间已过半，学生的心理和生理就会跌入低谷。另外，将脱式计算转换成竖式计算是多数学生的学习难点，也是学习的重点内容，本应该让学生爬坡而得到的竖式计算，却以教师的直接给出替代，冲淡了教学内涵。

如果将第二个因数换成质数，比如13，相应的第一个因数由14换成12（为规避难度叠加，本节课先学习不进位的两位数乘两位数），学生加减法时所学的“凑十法”和“破十法”的经验，以及简化计算的需求，会使他们将12×13转化为12×10+12×3，或是10×13+2×13，也可能想到（12×5）×2+12×3（第一项是整十数），这些都是良好数感的表现，而前两种算法为新课的学习起到了承前启后的作用。

情境的选取首先要考虑的是能够转化为学生已学过的，其次要能自然引入将要学习的内容。

三、第二次设计及实践

【学生前测】

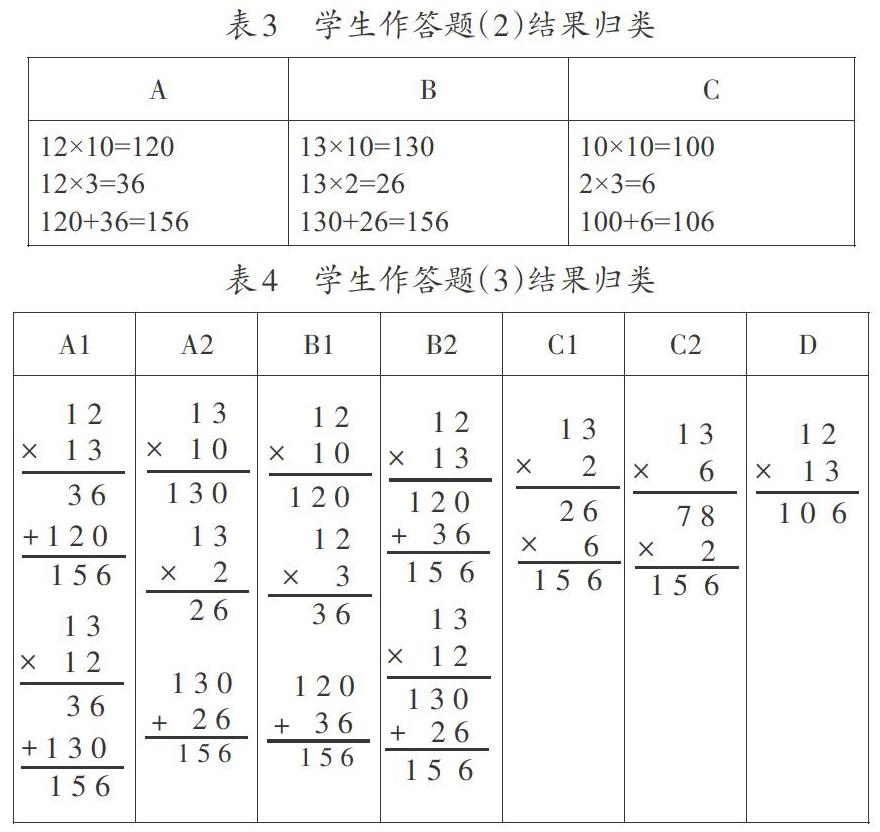
前测共3个题目：（1）每套12本书，买了13套，共买多少本，请列出算式（不计算）;（2）估算12×13，并写出估算的过程;（3）尝试写出12×13的竖式笔算。学生的作答归类，见表3及表4。

前测表明，学生能从实际问题中抽象出乘法模型，而且多数学生的转化正确，表明他们掌握了乘法的意义。多数学生能将其中一个两位数拆分为一个一位数和一个整十数，说明“凑十法”“破十法”，以及估算的经验，对此问题的转化起主导作用。但学生列竖式计算有困难，而且加减法的竖式笔算对学生两位数乘法竖式笔算有负迁移倾向。

【实践片段2】

依据前测，将12×13融入情境中（不出现文字信息），让学生经历发现提出问题、建构竖式笔算、巩固竖式笔算、了解“铺地锦”算法等活动。

1.发现和提出问题

只呈现花毽表演的点子图（每个点代表1人，如图2），让学生就情境信息提出问题并尝试回答。除了“一共多少人？”，学生提出的问题还有：每行多少人，一共多少行？每列多少人，一共多少列？

2.建构竖式笔算

师：对于问题“每行12人，共计13行，一共多少人”，列出算式是什么？

生（齐）：12×13。

师：前测让大家尝试写出12×13的竖式笔算，请看这两个竖式（表4中C1、C2类），你能读懂他们的算法吗？请用点子图圈一圈，判断他们的算法对不对。

（通过圈画，学生认同这两个竖式。不过学生L指出，如果第一个数是11，这个方法就失效了。）

师：学生L说得好，这个方法虽然挺巧的，但不具有普遍性。我们要寻找两位数乘两位数竖式笔算的通法。看看这个竖式（表4中的D类）可以吗？

生1：12×l0就得120，12×13不可能只有106，所以這个竖式不对。我看像是个位和个位相乘，十位和十位相乘，然后相加的。

生2：我就是这样算的，因为我将12拆成10和2，13拆成10和3，这样10×10=100，2×3=6，100+6=106。我觉得方法对，但得数不对，不知哪有错？

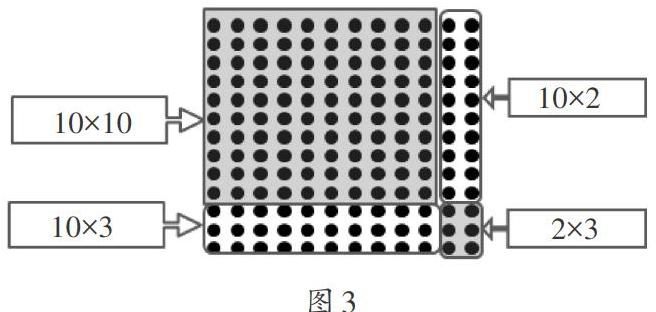
师：生，的方法听起来蛮有道理的，但是结果却不对，问题出在哪？请大家在点子图中圈一圈10×10和2×3，发现问题了吗？

生3：（如图3）缺了10×2和10×3。

师：怎么完善这个竖式（表4中的D类）？

（学生展示（略））

在对这些竖式的分类、算法和算理的共性和差异比较的思维碰撞中，学生完成了竖式笔算的建构。他们发现竖式笔算就是将第二个因数拆成易于口算的3与10，然后分别与第一个因数相乘再相加的脱式计算的简便写法，从而体会到数学突出本质求简之美。

【实践反思2】

第一次实践，算法多样化成为课堂教学的中心，挤占了学生独立尝试竖式计算，以及沟通算理和算法的时间。第二次实践，不仅将数据进行了相应调整，将算法多样化做了适当的删减，而且以学生前测中竖式计算的错误为情境，调动了学生积极探寻错因、完善竖式的欲望;在竖式的改进过程中有意驻留，让学生在比较、分析中发现合理的算法，使竖式笔算的建构真正成为教学重点，同时培养学生的数感。

四、思考建议

1.问题情境的选择

将学习内容融入问题情境中，既是培养学生数学建模的机会，也是发展他们数感的契机。为了突破难点，理解算法和算理，人教版和北师大版教材，都借助点子图帮助学生思考与验证。但据课堂观察，点子图对于三年级的学生而言还是抽象的。因此“两位数乘两位数”的内容中，“人”和“队伍”的情境更利于学生抽象成点子图，有时候适宜的情境可以达到事半功倍的效果。

2.算法多样化到优化

数据和情境是计算教学中重要的一环，好的数据可以带给学生算法多样化的可能，算法多样化可以培养学生的创新意识，同时培养学生的数感以及对于算理的理解。但在教学过程中盲目的“多”反而适得其反，因此算法多样化要适度，要让学生在“多”中选优。优化算法的过程是学生提升对于数与式的感觉的过程，亦是提升自身运算能力的过程。

3.算法与算理相随

算理是学生掌握算法的根，不少教师都在努力践行这一理念。然而，仅仅让学生明白算法的道理是不够的，还应该促进学生在建构算法的过程中理解算理。学生在此前学过加减法的竖式笔算，学过多位数乘一位数的竖式笔算，所以学生在教师的适度引导下是可以建构两位数乘两位数竖式笔算的。由于学生水平参差不齐，所以创设基于学生认知的“一波三折”的情境，让学生在思考与交流中自然地建构算法、理解算理就成为设计的关键。

4.学生调研的价值

必要的课前调研以及对于学生生成性资源的充分分析是开展有针对性课堂教学之本。课前调研可以使教师清楚学生的最近发展区在哪里;学生对于“数”的感觉，可以在调研中部分表现出来，为教师读懂学生提供基础。同时学生所呈现的错误答案是教师分析学生思维特点和思维发展水平的重要载体，可为有针对性地设计教学提供参考。

（责编 金铃）