发挥联想作用 深化数学理解

林玉芬

联想是指由一种心理过程引起与之相联的另一种心理过程的现象，也就是由一件事物想到另一件事物，由当前的事物回忆起相关的、以往的事物，或由一件事物引发想到另一件事物。巴甫洛夫认为，一切教学都是各种联想的形式。联想运用到教学中是指通过观察，分析、研究对象或问题的特点，与已有的知识和经验建立联系，找出事物的共性，探究解题思路，由此及彼。在数学课堂中恰如其分地联想，可以唤起学生对旧知识的回忆，沟通新旧知识之间的联系，促进知识的迁移和发展。联想能突破思维定势，创造性地找到解题策略;能触类旁通，有助于探究解题规律;能激发学生的学习兴趣，引发数学思考，深化数学理解，促进思维的高效发展。

一、情境联想，独创解题

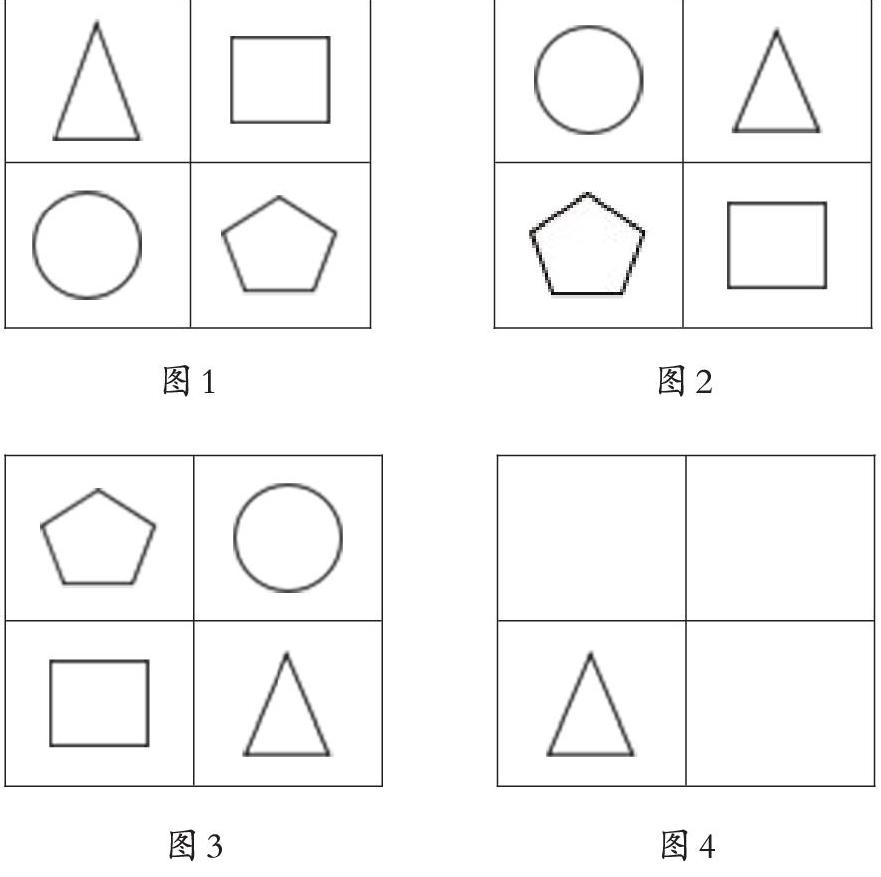
《义务教育数学课程标准（2011年版）》指出，数学学习活动要激活学生思维，培养学生独立运用数学知识思考与创造意识，促进学生创新能力的发展。课堂教学是培养学生创新能力的“主阵地”，而创新能力的习得离不开创造性思维的发展。创造性思维是一种与众不同的思考，它包括发现新事物、揭示新规律、创造新方法、解决新问题等思维过程。教师要鼓励学生从教材中走出来，打破课堂空间的狭窄性与单纯知识的空洞性瓶颈。可以启发学生运用情境联想，把生活与数学紧密联系，运用生活经验解决问题，从而形成对数学知识的理解和有效的解决问题的策略。情境联想是学生根据已有的知识和生活经验想到某个情境，使之成为解决某一问题的原型和依据。教学中，教师有意识地引导学生利用已有的知识、经验去联想，学生就能轻松地解决问题。如题：根据图1、图2和图3，把图4补充完整。

虽然大部分学生通过引导都会想到用旋轉的知识来解答，但由于有多个图形，学生在旋转过程中难免觉得有点乱。有一个学生由暑假去旅游，联想到可以让三角形、圆形、正方形和五边形也去“旅行”，把每个表格看作有四个不同的景点，每个图形都要玩这四个景点，哪个图形没到过哪个景点就补充进去。

这个学生运用情境联想，把数学问题与旅游联系，从而产生了新的解决问题的方法。这样，把数学与生活紧密联系，让枯燥的数学问题变得形象、生动、有趣，让数学变得简单好玩，还让其他学生也豁然开朗：原来数学问题可以用生活经验帮助解决。从而激发了学生学习数学的热情，调动了学生学习数学的积极性和主动性。

二、直觉联想，探索发现

直觉联想是在已有知识和经验的基础上，依据题目结构或图形的特点，观察分析，反复思考，突发灵感，联想顿起，使思路油然而生。在数学教学中，教师若能运用直觉联想去引导学生从已有的知识、经验展开联想，积极思考，进而发现规律，就能加深对新知识本质的理解。

三角形三边之间的关系，对四年级学生来说既陌生又熟悉，因为学生对三角形三边之间的关系有一定的生活体验，但又不是很明确。教学时，可以用白板先出示路线图，提问：小杨同学从家到学校有两条路可以走，请帮他选一选，走哪条路最近？

学生很快就找到了第二条路最近，但是对于原因，大部分学生是用两点之间线段最短来解释的，并没有发现与三角形的三边之间有关系;于是，我提示可以观察路线图。这时，有学生凭直觉猜想可能跟三角形的边有关系，因为这两条路恰好围成一个三角形。我顺势抽象出三角形的数学模型，再带领学生复习三角形的概念，突出围成即首尾连接，避免操作误差;然后，引发学生猜想：如果给你三根小棒当作三条线段，能否围成一个三角形呢？学生猜想后提出，可以动手操作来验证自己的猜想是否正确。

在动手操作、探究发现中可以设置三个环节：第一个环节是操作尝试，初步感知三根小棒不一定能围成一个三角形，那么“围成”与“围不成”会与什么有关呢？以问题驱动进一步探索。第二个环节是讨论交流，探究规律， 学生先分小组讨论研究如何比较三角形三边之间的关系，再全班交流，并明确研究方向为“每组都要任意两根小棒的长度之和与第三根小棒比较”;接着，学生进行小组活动，填写实验报告单;合作完成后，各小组汇报自己的发现，重点引导学生根据数据比较的结果理清“围成”与“围不成”的理由;最后，总结三角形中任意两边之和大于第三边。第三个环节是再次质疑，验证规律，是不是所有的三角形任意两边之和都大于第三边呢？有什么办法证明呢？学生经过思考，确定在练习本上随意画三角形并通过量、算进行独立研究。我引导学生对这些三角形进行分类研究，借助不完全归纳法，推出前面发现的结论具有普遍性，是正确的。这样，学生通过小组合作实践操作、观察、思考，发现规律，并亲自体验“在一个三角形中，任意两边之和大于第三边”这一结论的普遍性。

学生利用自己的直觉进行假设、猜想，再通过验证来证实自己的假设，最终总结规律，探索出解决问题的新方法，使原有知识结构得到补充、改造和逐步完善，拓宽了知识领域，培养了创造性思维。

三、类比联想，生成模型

类比联想是把类似的问题放到一起进行对比，使学生受到启发，进而产生联想，发现规律，生成模型。它往往能把复杂的问题简单化，让学生更深入地理解数学本质。

在教学“乘法分配律”时，我首先利用多元表征，引导学生初探意义。给学生提供探究单，里面有现实原型：上衣每件42元，裤子每件38元，买了5套;有几何模型：大长方形的长7米，宽2米，小长方形的长3米，宽2米;有棋子图。学生根据情境图的数学信息提出问题，并确定要解决的问题是：①买5套这样的衣服要用多少元？②他们的面积一共是多少平方米？③一共有几个棋子？学生选择其中的一个问题用不同的方法列出综合算式并解答，交流汇报每种算法的解题思路，结合课件重点理清每一步表示的意义。这样，通过引导学生感悟多元数学表征，并在讨论交流、补充质疑中，深入理解算理，就形成了对乘法分配律初步的感知。

其次，利用表征，生成模型。本环节有三个活动。第一个活动是分类整理，初次建模。我提出问题：“你会对这些算式进行分类吗？”学生通过观察思考，独立对这些算式进行分类，并说清分类理由。根据算式结构分类，一类是两个数的和乘以一个数，一类是一个乘数分别与两个数相乘，再把积相加;沟通这些算式之间的联系，把计算结果相等的两个算式用等号连接起来;启发思考：为什么左右两边算式不一样，可结果却是一样呢？引导学生运用乘法的意义解释。如，第一个问题左边是求80个5是多少，右边是用48个5加32个5也等于80个5，发现这三个等式的左右两边都是求相同的几个几所以才相等;比较左右两边算式的异同点，发现相同因数与不同因数。

这样，通过分类整理，让学生聚焦算式、观察特点，发现两类算式的不同结构特征;再通过寻找有联系的两个算式，感受等值变形的特点，初步发现规律，即一个数乘两个数的和等于这个数分别乘这两个加数所得的积的和。

第二个活动是再次建模，验证规律。我引导学生质疑：像这样的等式还有吗？针对这个问题分五步走，一是播放乘法分配律的小故事;二是进行猜想游戏，让学生根据课件出示的算式，推想出结果与之相等的不同算式;三是学生独立仿写算式，分别算出每个算式的计算结果，验证等式是否成立，再小组交流;四是收集展示学生作品，并思考这些等式有什么共同特点，发现他们都是一个数乘两个数的和等于这个数分别乘这两个加数所得的积的和，反之也成立;五是学生发挥想象，结合具体事例，通过图示（方块图、线段图、点子图等），进一步理解前面发现的规律。

第三个活动是建构模型，表述规律。我提出问题：“能用一个等式表示出所有的等式吗？”让学生可以用图形、文字或者是字母等各种符号试着来写一写、画一画;在交流中，学生创造了多样化的、富有个性的表示方法;学生通过比较个性化的符号表示，认为统一字母表示方法最简洁。

学生经历了一个由具体数值计算到符号表达的过程，通过问题情境、发现规律、举例验证、规律表达。引导学生经历提出问题、探索发现、建立模型、简化模型的建模过程，还引发了更多的学生关注到算式的变化规律，促进了自主创造。通过多种方式解释验证，以内在不变的“理”，理解外在变化的“形”，经历从具体到抽象，从个别到一般的建模过程，并渗透数形结合思想、由特殊到一般的数学思想，发展了逻辑思维能力及推理能力。

四、方法联想，扩散思维

方法联想是将数学中常用的解题方法、思路互相灵活地联想运用，扩散思维。教学中，教师坚持不懈地引导学生从已有知识、方法联想到与之相似、接近的知识、方法，把学生的求知欲与思考引向新的领域，可以使学生逐步形成由此及彼的联想能力，以激发求異意识，引导学生离开原有的思维轨道，联想到别的思维方式，实现求异思维。

有这样一道题：一个铁块体积为500立方厘米，完全浸入棱长为10厘米的正方体容器的水中，若原来水深7厘米，水会溢出吗？学生用了两种方法来求解：一是先求出水的体积和铁块的体积一共有多少立方厘米，再求出正方体的容积，最后进行比较，发现水会溢出，计算溢出了多少立方厘米;二是先求出正方体容器剩下的空间，再与铁块的体积进行比较。在用这两种方法解答后，我提问：“还有其他方法吗？”整个课堂中一片寂静。我提示：“能从高度直接比吗？”经过启发，学生跳出了原有的思维方式，用铁块的体积（上升的水的体积）÷正方体容器的底面积=上升的水的高度（5厘米），再用5+7-10=2厘米，由此判断水会溢出。当学生能从多角度思考问题，灵活、贯通地用不同的方法解决问题，并进行对比时，他们就能发现比较优化的方法，提升了思维能力。

总之，联想是一种重要的思维方式，在小学数学教学中，运用联想教学法，可以使抽象问题具体化，可以建立知识之间的内在联系，指引学生由此及彼，提高新知的发现能力和创新能力，让数学课堂充满活力，让学生思维充分发展。

（责任编辑：杨强）