二次型正定性在多元隐函数极值中的应用

王国兰，贾庆菊

二次型正定性在多元隐函数极值中的应用

王国兰，贾庆菊

（山西工商学院 计算机信息工程学院，山西 太原 030006）

利用二次型的正定性及隐函数的存在定理，给出了多元隐函数极值存在的必要条件，得到了一个快速判断多元隐函数极值的新方法。

矩阵；正定性；多元隐函数；极值

1 问题的提出

在管理科学、最优设计、系统控制等许多领域中，很多实际问题目标函数或约束条件很难用线性函数表达。解决这种问题要用到非线性规划的方法，如果非线性规划的最优解存在，自然离不开多元函数极值的讨论。一般教科书仅限于二元函数极值判定的讨论，文献[1]仅给出了多元显函数极值问题的讨论。本文利用二次型的正定性及隐函数存在定理，给出了多元隐函数极值存在的必要条件和充分条件，得到了一个快速判断多元隐函数极值的方法。

2 引理

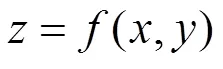
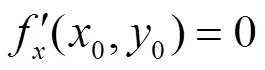
令

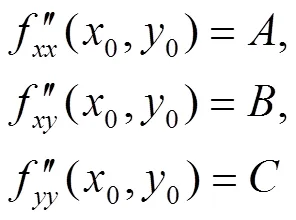
则

引进矩阵

在驻点

某邻域内连续且有一阶二阶连续偏导数。令矩阵

3 定理及其证明

定理1 设函数

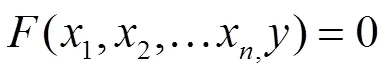
则由方程

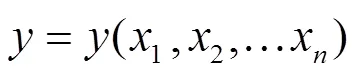
证明 由题设知

是

的驻点，即

同理，

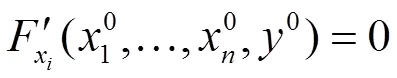
证毕。

定理2 设函数

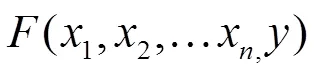
在驻点

某邻域内连续且有一阶、二阶连续偏导数。

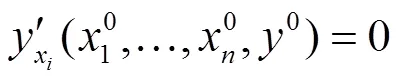
其中

(3)

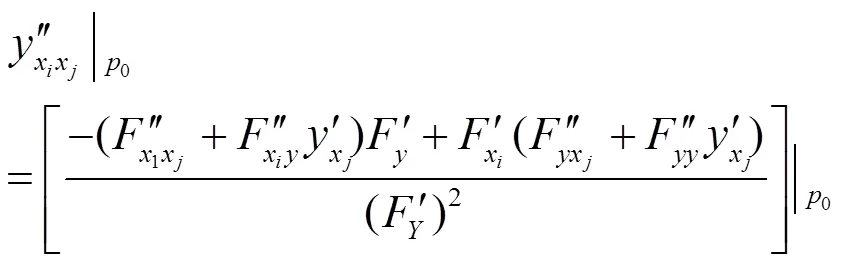
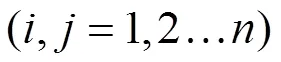
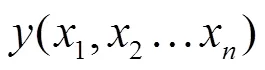
在0处取得极小值。当(0)为负定矩阵时，函数

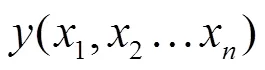
证明 由已知

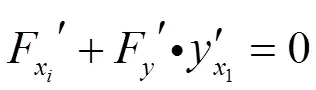
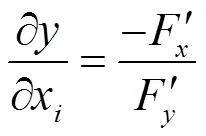
若在

处有

由引理2可知结论成立。证毕。

4 定理的应用

例 求由方程

解 令

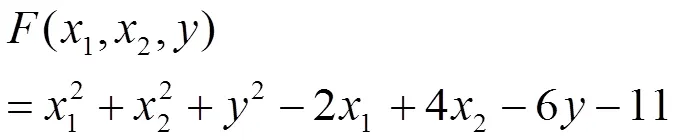
解方程组

得驻点1(1,-2,8)，2(1,-2,-2)。

在驻点处，有

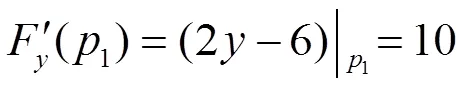
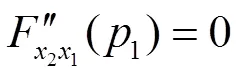
显然

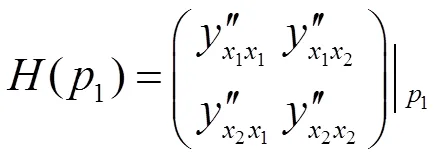
代入数值，得

同理

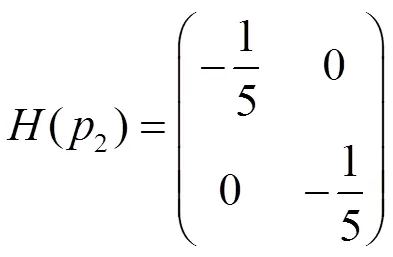
显然(1)为正定矩阵，(2)负定矩阵，由定理知

[1] 同济大学数学系.高等数学(第六版,下册)[M].北京:高等教育出版社,2006:110-111.

[2] 申玉发.矩阵的正定理论在多元函数极值问题中的应用[J].郑州航空工业管理学院学报,1996,14(3):59-62.

[3] 李忠艳,陆忠臣,陈浩.一类多元函数极值的快速判别方法及应用[J].数学的实践与认识,2003,33(7):96-101.

[4] 叶振信,张浩明,杨浩,等.基于次型正定性多元函数极值判别法[J].数学的实践与认识,2014,44(23):303-306.

The Application of Quadratic Positivity in the Extremum of Multiple Implicit Functions

WANG Guo-lan, JIA Qing-ju

(Computer and Information Engineering College,Shanxi Technology and Business University, Taiyuan 030006, China)

In this paper, by using the positive character of quadratic form and the existence theorem of implicit function, we give the necessary condition for the existence of extreme value of multiple implicit function, and get a new method to judge the extreme value of multiple implicit function quickly.

matrix; positive qualitative; multivariate implicit function; extremum

O174

A

1009-9115(2019)06-0037-03

10.3969/j.issn.1009-9115.2019.06.009

山西省教育科学“十三五”规划课题（GH-17083)

2019-05-21

2019-10-09

王国兰（1981-），女，山西太原人，硕士，副教授，研究方向为基础数学。

（责任编辑、校对：赵光峰）