自动确定类别数的RJMCMC+SA图像分割算法研究

张文坤，汪西原,2，韩佳雪

(1.宁夏大学物理与电子电气工程学院，宁夏 银川 750021；2.宁夏沙漠信息智能感知自治区重点实验室，宁夏 银川 750021)

全色遥感图像分割和分割过程中类别数的确定是重点问题。图像分割方法主要分为基于阈值、区域、边缘、聚类的分割方法等[1]，从数学角度分析，其将数学函数离散化或者将数字图像连续化，进行数学意义上的分割，在物理意义上无法解释部分算法中一阶或二阶不可导等问题[2]；从图像本质分析，基于阈值的分割方法忽略了图像的空间特征，基于区域的分割方法需要人为指定种子点来获取全局最优解，基于统计学的贝叶斯模型，其对数字图像建模，将每个像素值看作一个随机变量，求其最大后验概率分布，实现稳定可靠的图像分割。图像分割中类别数的确定多采用聚类方法，基于近邻间的关系找出不同特征族群，对数据进行划分，但易受聚类中心的个数及初始聚类中心的影响。基于遍历的径向基函数(radial basis function，RBF)网络能够实现非线性映射，其隐含层单元将非线性可分的输入空间变换到线性可分的特征空间，输出节点数代表分类数，但隐含层基函数的中心选择和宽度很难准确选择且参数的数量影响模型的复杂度，很难自动确定类别数。

综合分析RBF网络与非线性回归模型的特点，本文利用贝叶斯理论将非线性回归模型中基函数的参数视为具有某种已知先验分布的随机变量，根据参数的先验分布建立图像分割的后验概率分布模型。

为计算后验概率，一般方法是贝叶斯置信传播、图切等[3]。贝叶斯置信传播用于有向无环图模型的概率推理，也可用于无向图模型，如马尔科夫随机场(Markov random field，MRF)。贝叶斯网络中的先验知识可能属于同一集群，而极大似然估计在图像分割中没有考虑数据分组时的概率和空间约束问题，因此将MRF模型和贝叶斯置信传播相结合[4]，求解最大后验概率估计中的交互势函数，可实现分割结果区域一致性，并且通过学习局部间的联系得到全局最优解，但会夸大待求节点的边缘影响，为保证贝叶斯网络中节点的完整性，将贝叶斯网络与多尺度理论结合的多尺度贝叶斯网络模型[5]更加有效，而在模型尺度选择上无法准确固定树的层数且算法复杂度较高。

为此，本文结合GREEN[6]提出的可逆跳马尔科夫蒙特卡洛算法(reversible jump Markov Chain Monte Carlo，RJMCMC)模拟该后验概率分布，构建灵活、全面的RJMCMC混合转移核，完成后验概率估计。根据雅克比行列式思想构建适当的接受概率，实现不同参数的“维度-匹配”，使混合转移核在不同维度参数空间之间跳转，并采用模拟退火理论(simulated annealing，SA)来约束优化转移核跳出局部最优达到全局最优，进而计算出径向基函数的个数和参数，完成图像类别数的确定和分割。在图像分割前利用高斯曲率滤波(Gauss curvature filtering，GC)原理[6]对图像进行几何平滑预处理，进一步避免了模型优化过程中陷入局部最优，取得很好的分割效果。

本文运用经典的信息准则(Akaike information criterion，AIC)、贝叶斯准则(Bayesian information criterion，BIC)、最小长度描述法(minimum description length，MDL)和H-Q信息准则(Hannan Quinn criter，HQC)选出4种基于遍历的RBF分割模型和4种分割算法，分别与RJMCMC+SA算法进行对比实验，结果表明本文算法具有很好的复杂度和精确度且能够自动确定图像类别数。

1 图像预处理及模型参数估计思想

1.1 GC图像平滑处理需求

在非线性回归模型中参数的选择和优化始终存在局部极值问题，为使优化函数跳出局部最优解取得全局最优，KRIZHEVSKY等[7]提出了预训练和微调理论。本文引入GC理论，在分割之前对图像进行预处理。GC理论是一种具有边缘保护的图像平滑算法，充分利用了图像的离散特征、微分几何的连续理论，其假设图像各块曲面是分块可展的，使用已知的几何曲面来优化其对应的正则项，并利用图像的离散特性来隐式地优化曲率，即减小曲率而无需计算曲率，避免了计算复杂的几何流且滤波运算的复杂度大幅度降低，具有很高的执行效率。

图像的GC处理中，利用3×3的滑动滤波窗口，平滑图像中的像素点，如图1所示。

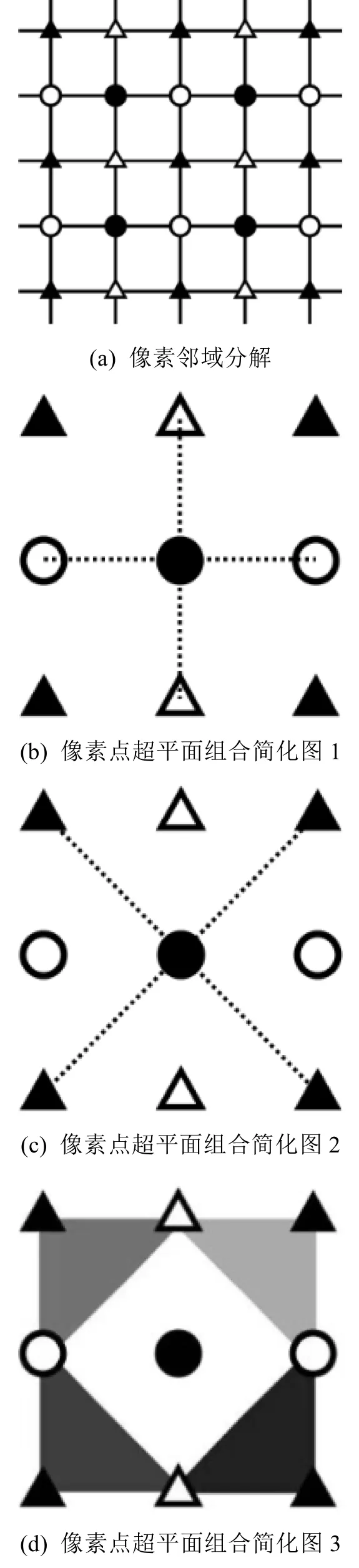
图1 高斯曲率滤波变分模型示意图

GC根据邻域像素构成的切平面中的最小距离修正调整像素值。对图像中的极大值和极小值像素进行约束，降低像素的峰值、提高鞍点与谷值，保留其整体状态，对图像进行几何优化，使分割优化过程中在学习率变化不大的情况下，尽可能避免陷入局部最优状态。

1.2 后验概率分布及其参数估计方法

一幅全色遥感图像S，设为定义在图像像素s上的标号场，其中，s为像素位置，Xs为定义于s上的随机变量，为像素s的特征标号；设为定义在s上的特征场，其中，Hs为标号为xs的像素强度，分别为X，H的实现；定义为类别。设隶属于类别k的像素标号集为如果Xk为空集，则对应类为空类；反之为实类。

多元参数映射模型采用Holmes和Mallick近似方案，构造非线性回归模型M(model)，即

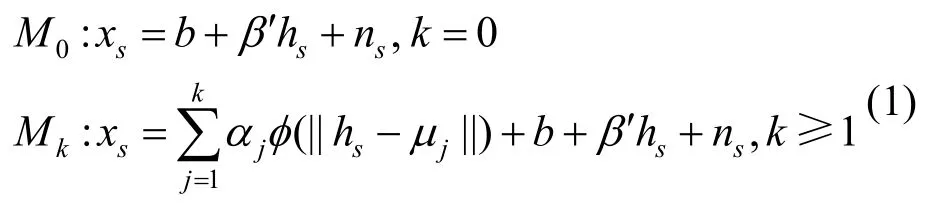
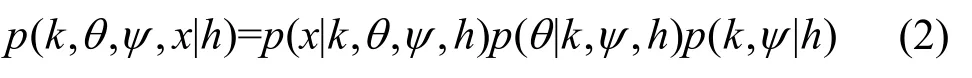
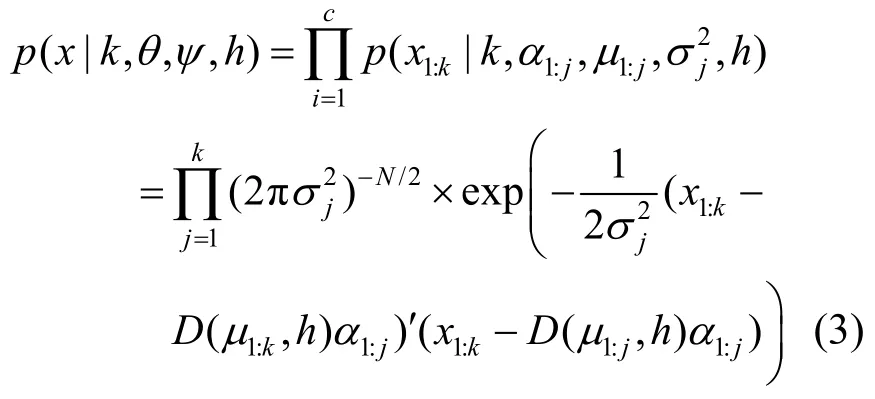
其中，D为参数矩阵化形式。尺度参数2σ服从共轭逆伽马先验分布系数α1:j服从方差为，期望为0的高斯分布；尺度参数δ2服从模糊共轭先验参数超参数Λ服从无信息共轭先验分布先验模型阶分布是一个有约束的截断泊松分布。模型先验分布为

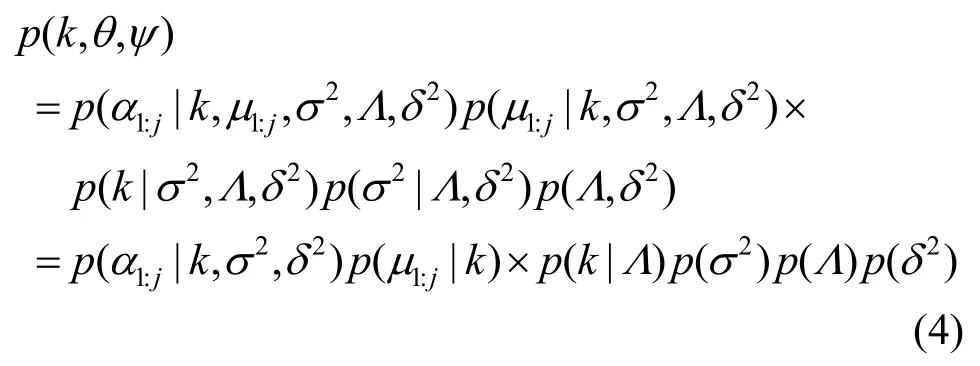
对参数进行积分，得联合后验分布归一化常数表达式为

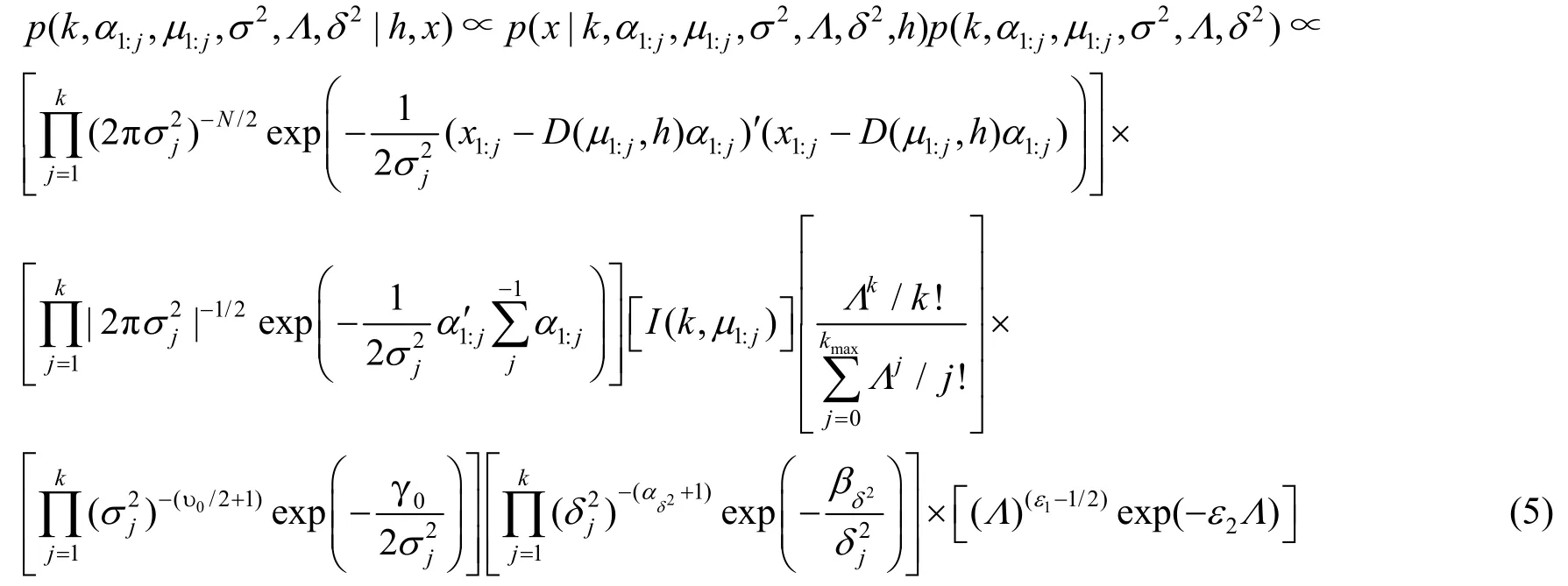
2 图像分割模型的建立过程

2.1 全色遥感图像的标号场模型

假设Xs为独立分布的，且满足 Gaussian概率分布，则X的概率密度函数为

其中，aj为常数，表征s邻域特征标号的作用强度；Ns为像素s的邻域像素集合；I为指示函数，有

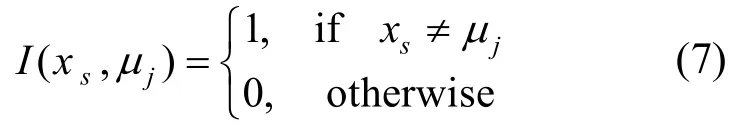
2.2 图像模型的建立

对于全色遥感图像，假设其像素强度Hs为独立分布，且Hs满足Gamma分布，则H的概率密度函数为

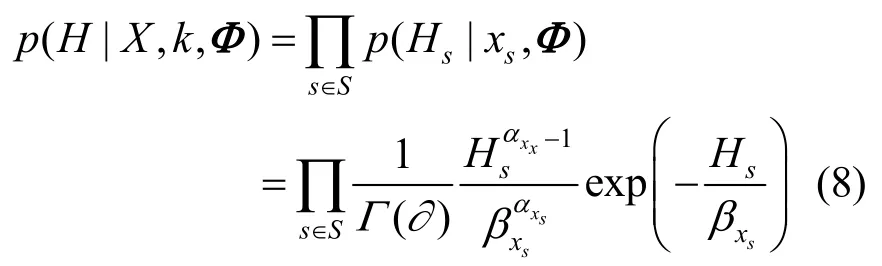
其中，()Γ·为Gamma函数；参数矢量式(8)刻画出图像中像素点的近似概率，结合式(2)，完备刻画出图像分割对象的服从概率，设整合参数向量则联合后验概率为

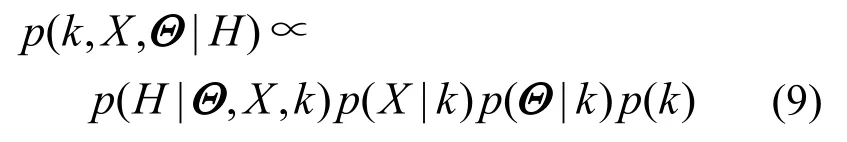
3 RJMCMC+SA算法原理及其实现

3.1 不同维度下参数空间的“维度-匹配”

联合后验概率(式(9))需对参数中非线性函数的高维积分进行评估，由于参数空间的维度不同，为解析地获得不同维度下的参数空间计算，实现不同参数的“维度-匹配”，采用建议接受率在马尔科夫蒙特卡洛算法(Markov chain Monte Carlo，MCMC)中构建一个非周期的马尔科夫转移核p(x,y)，定义一个特征分布π(x)，在细致平稳条件下采用Hastings算法[9]来解决转移核和π(x)分布问题，则其建议接受率为

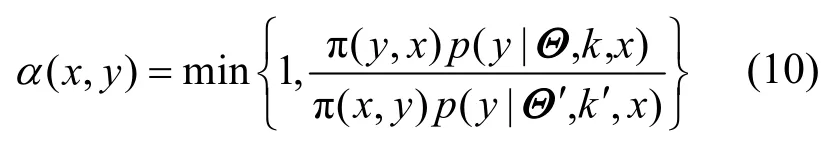
假设2个参数空间维度分别为m1和m2，在参数空间中存在一个奇异测度 π，则联合平稳建议分布为为满足细致平稳性和参数奇异自洽性，定义一个自由向量u和当前参数θ，在 2个子空间中不同子空间中式(10)改写为

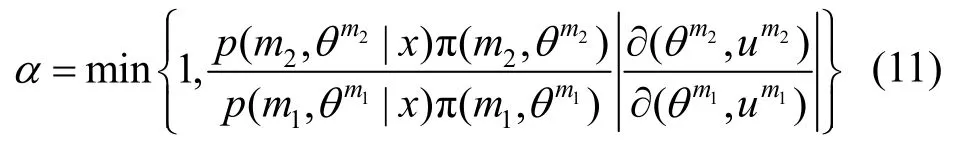
3.2 RJMCMC混合转移核

RJMCMC混合转移核由生成、删除、分裂、组合、特征标号转移组成。假设类别数k是变化不固定的，混合转移都是自由移动，其分布分别为其中0≤k≤kmax。当k=0时，；k=1时，时，生成和删除的接受率概率为

其中，p(k)为模型Mk的先验分布，c是调整尺寸移动比例的常数。

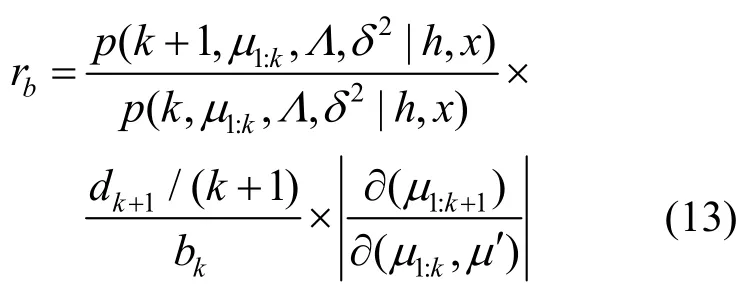
同理，删除概率移动为

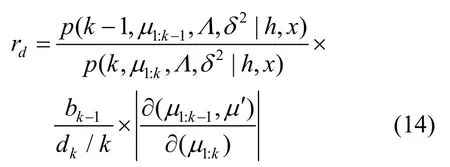
接受率为

组合操作随机选择基函数中的一个μ1和其相邻的μ2，根据Euclidean距离公式计算出2个参数的勒贝格测度保证其可逆性，分裂操作为

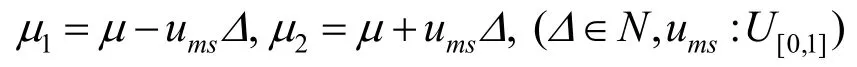
分裂概率移动为

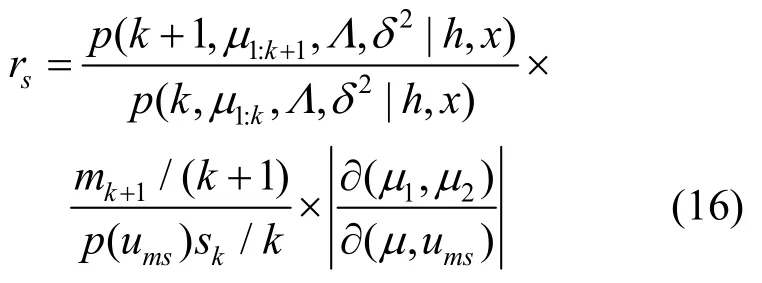
同理，组合概率移动为

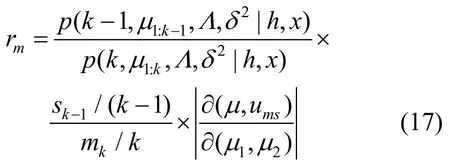
接受率为

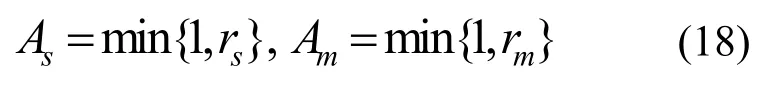
特征标号转移也就是RBF中心的更新，根据式(5)得特征场是一个基函数的全概率分布，即

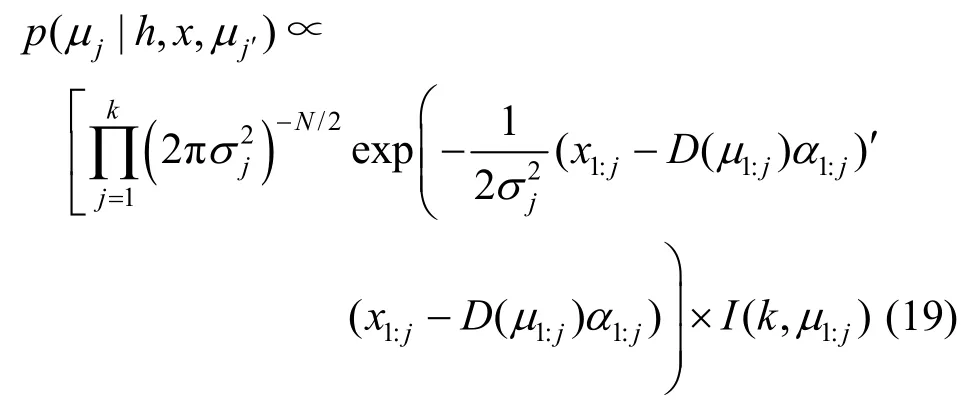
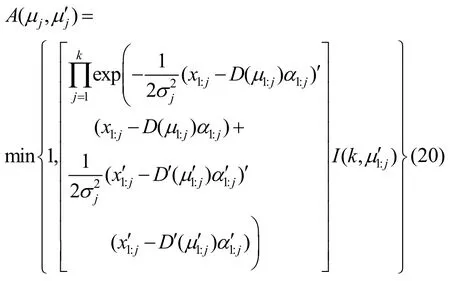
3.3 RJMCMC+SA算法的实现

RJMCMC算法[10-11]能够在参数空间中寻找到像素邻域模型解空间的最优解，SA结合概率突跳特性在解空间中随机寻找类别目标函数的全局最优解。

SA模拟非齐次马尔可夫链[12]，状态z在迭代i处的不变分布为为温度下降进程且。在弱假设正则化下，根据Metropolis-Hastings(MH)算法，马尔科夫链从状态z转移到状态z′的过程中，建议分布为

假设可逆跳跃的齐次转移核为,κ（z′ z），其状态分布满足，则RJMCMC+ SA的建议接受率为

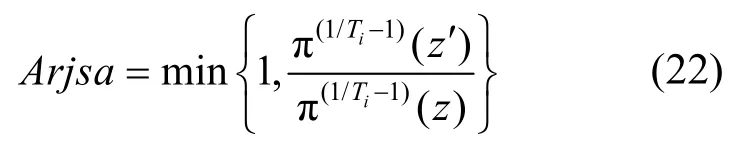
RJMCMC+SA算法的实验流程如下：

步骤1.遥感图像初始化，利用GC算法对图像进行平滑处理，设定图像Hs,xs。

步骤2.初始化混合贝叶斯概率模型中的参数迭代次数i；设定均匀分布u：U[0,1]，温度下降进程Ti。

步骤3.

则执行“生成”(式 13，15)；

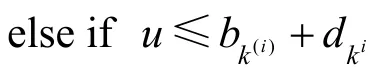
则执行“删除”(式 14，15)；

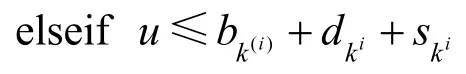
则执行“分裂”(式 16，18)；

则执行“组合”(式 17，18)；

else 更新径向基函数的中心(图像特征标号，式(20))；

end if。

步骤4.执行MH算法，SA运算(式(22))。

步骤5.迭代次数i←i+1，返回步骤3。

步骤6.计算径向基函数的系数。

步骤7.通过步骤3～6计算出分割模型中图像每个像素Hs符合类别X的径向基函数；优化径向基函数及其参数，取得X属于Xk全局最优解空间，得出K个径向基函数。

4 RJMCMC+SA算法评价

4.1 RJMCMC+SA算法的数据拟合性和复杂度

采用AIC，BIC，MDL和HQC选择的4种基于高斯核函数训练得到的 RBF图像分割模型和GC预处理下的RJMCMC算法、RJMCMC+SA算法进行质量检测对比，分析其复杂度和数据拟合能力(即似然函数)。模型评价策略依赖最大似然估计，对于一个模型Mk，其最优评价是似然估计与惩罚项的和为

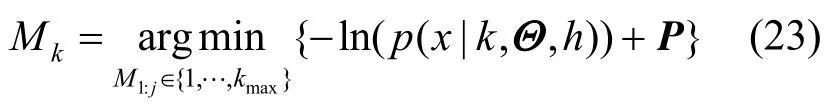
其中，Θ为模型的估计参数；P为模型的惩罚项。AIC解决模型的拟合数据优良性和复杂性之间的平衡问题；BIC的惩罚项比AIC大，避免出现维度灾难；MDL判别力求在模型精度和复杂度之间寻找平衡；HQC可避免小因素而忽略最优估计概率，其在贝叶斯方法中的渐进性比较好。定义ζ为模型的参数数量，4种模型选择方法可表示为

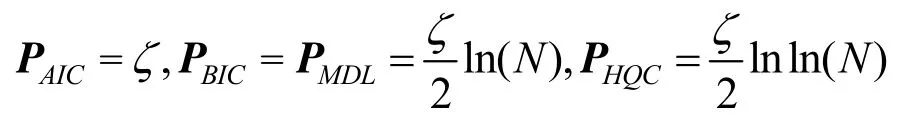
实验流程如下：

(1)初始化，即设定迭代次数5 000，kmax=50；

(2)迭代，即

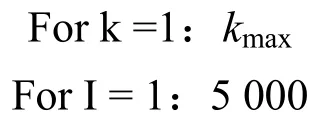
随机选择中心点μ1:k，在测试集数据上计算丢失率(Loss)，更新模型，在训练集数据上计算丢失率。

(3)根据不同的选择方法来确定模型，即

丢失率(Loss)=均方误差(mean-square error,MSE)

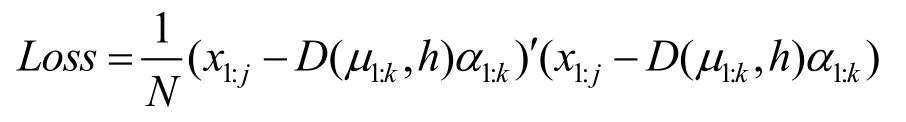
实验选取伯克利大学实验室图像分割数据集BSDS500和 GF-2号全色遥感影像(谱段范围0.45～0.90 μm、空间分辨率1 m)，不同分割方法下的实验结果见表1和表2。分析表中数据，在普通图像数据集上RJMCMC+SA算法相比AIC选出的最优RBF模型和RJMCMC算法，RBF的个数、数据损失量差别不大，且相对较低。在信息量大、细节丰富的GF-2号全色遥感图像上，RJMCMC+SA算法相比HQC选出的最优RBF模型，RBF个数减少 250个，测试数据损失下降 3.09个点，且比RJMCMC算法在测试数据Loss和收敛速度方面得到进一步提升，说明在处理全色遥感图像时RJMCMC+SA算法在数据拟合方面优于传统 RBF网络模型，同时表明SA在约束优化RJMCMC混合转移核过程中，在基函数的中心点和个数方面取得优异效果。相比AIC、BIC、MDL方法通过增加惩罚项来实现数据拟合优良与复杂性的平衡，RJMCMC+SA算法在贝叶斯推断中，其转移核不仅在高低维参数空间跳变不断调整后验概率参数，而且进行了SA优化，在拟合基函数参数和基函数的选择方面更加准确。对比分析表1和表2，在收敛速度上，RJMCMC+SA算法明显快于其他5种算法，因为应用到模型集的核函数中心产生方式不同，虽都需要遍历所有中心点，但前5种算法基函数中心的选择是在μmin:μmax之间随机产生，RJMCMC+SA算法是在μj:μj+1之间通过Euclidean距离计算得出，因此 RJMCMC+SA算法比其他算法收敛快，计算复杂度低。

表1 伯克利大学实验室数据集上的实验结果

表2 GF-2号全色遥感图像上的实验结果

4.2 RJMCMC+SA算法自动确定图像类别数

采用本文算法对伯克利大学实验室数据库的一幅图像和GF-2号全色遥感图像进行分割，在图像类别数稳定后，取算法前100次迭代数据，分析其对应的图像类别数变化情况，如图2所示。伯克利大学实验室数据库一幅图像中迭代次数在 1～30时，类别数在0～7之间跳变，从30次以后稳定为4类且与人工标记的图像类别数一致。GF-2号全色遥感图像中迭代次数在1～50时，类别数在0～8之间跳变，从50次以后稳定为5类且与目视结果相同。综合图可知，图像类别数可很快收敛到实际类别数。

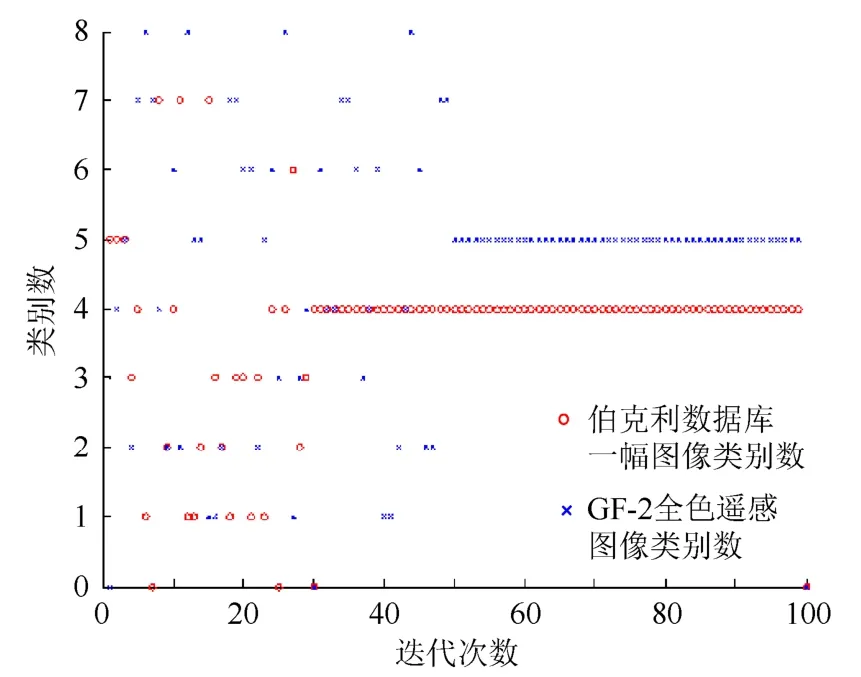
图2 不同迭代次数下图像类别数变化

图像分割完成前，在不同的迭代次数下，类别数不确定、分割区域不明确。RJMCMC+SA算法在确定类别数的同时还对分割结果进行了优化。对比图中红色实线区域分割结果，RJMCMC+SA算法分割下，伯克利大学实验数据库一幅图像(图(a1)～(b1))迭代次数分别为 10和15，全色遥感图像(图(a4)～(c4))迭代次数分别为10、15和30时，图像类别数不稳定、分割区域不明确，而分别在30次和50次迭代之后，类别数稳定且分割结果明显优于之前。因为 RJMCMC+SA算法在确定类别数的过程中，在SA温度下降进程的约束下，执行分裂和合并操作，对RBF中心点进行特征标号移动操作，合并相似幅值的基函数，不断更新RBF的中心点，加强了类别分割精确度。

4.3 RJMCMC+SA算法与阈值分割算法比较

选用迭代自组织数据分析算法(iterative selforganizing data analysis techniques algorithm，ISODATA)、GC+ISODATA算法、最大类间距算法、Color Slices算法和RJMCMC+SA算法进行比较，证明本文算法的优越性。

在图2所示的实验中，得出在迭代50次后分割结果趋于稳定，因此，在实验中5种算法均迭代50次，完成全色遥感图像分割，并对比分析，如图4所示。ISODATA算法、GC+ISODATA算法分割结果模糊，抗噪声差；最大类间距算法分割明显，但是无法确定图像类别数，不同类别的地物划分为了一类；Color Slices算法能够分割出多种不同地物，类别数过多，相似地物划分为了多个类，导致分割杂乱，出现过分割现象，分割结果不精确；RJMCMC+SA算法相对以上算法效果明显优异，地物目标分割清晰，噪声少，分割精确度高，适合全色遥感图像分割。

图3 不同迭代次数下的分割结果

图4 5种算法的分割结果

4.4 RJMCMC+SA算法定量评价

选择ISODATA算法和本文算法进行实验并求其混淆矩阵，作定量评价。ISODATA算法在径向基函数中心点的选择上：当图像中属于某个目标类别的像素点数过少时删除此类别，当属于此类别的像素点数过多且分散程度较大时则分裂这个类为两个子类别。其在基函数中心选择上与本文算法具有类似思想。

分析表3和表4所得的混淆矩阵[13]，RJMCMC+SA算法比ISODATA算法的用户精度、产品精度高，且 Kappa系数和总精度分别高 0.49和36.7%，说明RJMCMC+SA算法在分类精度方面优于 ISODATA算法。采用 GC进行图像平滑后ISODATA算法分类的Kappa系数和总精度分别提高0.18和13.9%，见表3和表5，因ISODATA算法在径向基函数中心点(聚类中心点)的选择上忽略了像素的空间特征，在类边界处像素强度变化剧烈且被动扩散性影响下，容易陷入局部极值，GC平滑了像素点且抑制被动扩散，提高了算法的精度，说明在GC平滑滤波后提高了聚类中心点的选择准确性。分析表4和表5数据，在经过GC处理后，RJMCMC+SA算法分割的 Kappa系数和总精度分别比ISODATA算法提高0.31和22.8%，表2实验数据已然表明 RJMCMC+SA算法在基函数中心点选择上相对4种模型的优越性，再次对图像全局像素点峰值和谷值进行GC平滑预处理后，产品精度和用户精度均大于85%且Kappa系数大于0.9，说明GC+RJMCMC+SA算法的分割精度更高。

表3 ISODATA算法分割的混淆矩阵

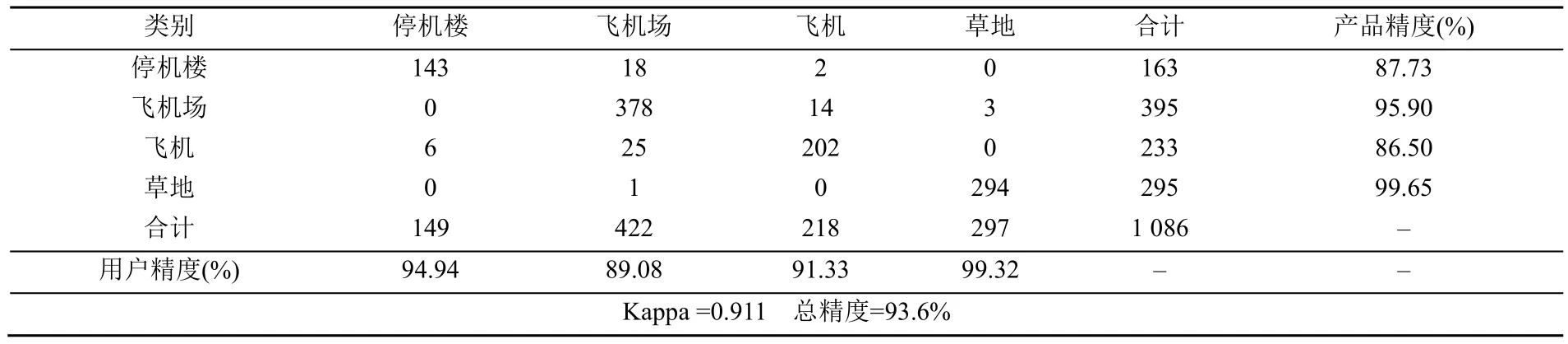
表4 GC算法预处理后RJMCMC+SA算法分割的混淆矩阵

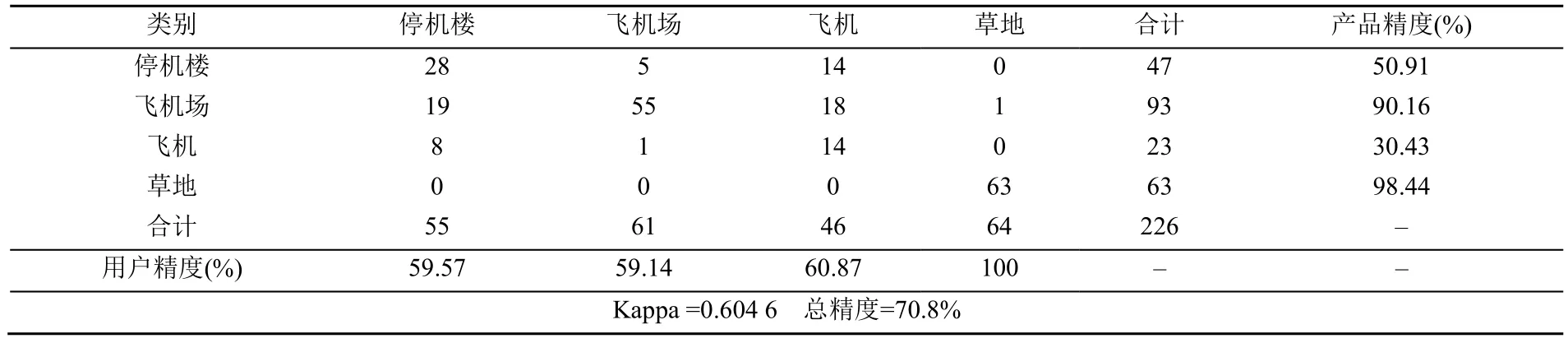
表5 GC算法预处理后ISODATA算法分割的混淆矩阵

5 RJMCMC+SA算法主观评价

AIC、BIC、MDL和HQC选择的4种模型及GC+RJMCMC+SA算法分割结果对比。

观察分析图5(a1)～(f1)，针对细节较少、图像复杂度低的伯克利大学数据图像，4种模型和RJMCMC+SA算法均能实现显著目标区域的分割，由于4种选择方法的惩罚项不同，图(b1)中AIC选择的模型的分割效果相对于其他3种分割模型最优，蓝色框中区域的噪声最少，红色框中的细节分割明显，RJMCMC+SA算法亦能达到优异分割效果。在GF-2全色遥感图像实验中，4种模型的分割结果差异明显，出现混分、错分现象，如图5(b2)～(e2)中飞机场停站楼及飞机(红色实线边框)区域，本文算法相比4种模型的分割结果具有低噪声，清晰度高的优势，更适合处理全色遥感图像。

图5 4种分割模型和RJMCMC+SA算法的图像分割结果

图(a2)～(d2)与图(a4)～(d4)为 ISODATA 算法和RJMCMC+SA算法在10～50次迭代次数下对同一全色遥感图像的分割结果，在同样的迭代次数下，ISODATA算法相比RJMCMC+SA算法出现错分和过分割现象，当迭代到 50次时本文算法分割效果明显趋于稳定，分割区域清晰、准确，能够清晰地分割出 3个油罐、厂房和道路，而 ISODATA算法的分割类别数混淆，精度差。在细节信息更为复杂的全色遥感图像下，如图(a3)～(d3)所示，ISODATA分割结果模糊无法分辨，且收敛缓慢、类别混乱不准确，细节分割错误；迭代次数同为50时，如图3(d3)与图5(f2)所示，RJMCMC+SA算法可清晰分辨出目标类别，说明本文算法分割的有效性和准确性高。

6 结束语

本文算法构建一种基于非线性回归模型的RJMCMC+SA图像分割算法。首先对图像进行GC平滑处理，在几何上避免了局部极值问题，然后利用 RJMCMC+SA算法实现贝叶斯形式化后的后验概率分布，进而确定径向基函数的参数和个数，完成全色遥感图像中地物目标类别数的自动确定和分割。解决了非线性回归模型中不同参数维度空间的跳变、模型冗余、模型可行性和复杂性不平衡、分割不稳定性、计算收敛速度慢等问题。相比传统的分割算法，本文算法综合像素强度、位置特征、参数相关性、空间特征，在处理信息量大、复杂度高的全色遥感图像方面取得更大的优势，更适合全色遥感图像的分割。