基于信息熵的风格绘画分类研究

钱文华 ，徐 丹 ，徐 瑾 ，何 磊 ，韩镇阳

(1.云南大学信息学院，云南 昆明 650504；2.云南大学研究生院，云南 昆明 650504)

不同艺术绘画风格具有不同的艺术表现力，尤其是名家艺术作品往往具有较高的艺术价值和传承价值。受到自然灾害、人为等因素的影响，艺术绘画作品也在加速破坏与消失。文化遗产数字化有利于不同种文化遗产的保护和传承，有利于艺术绘画作品的数字化保护，其中，艺术绘画作品的数字化分类和管理是文化遗产数字化保护的重要环节，将为文化遗产、文化作品的数字化存储、修复、推广和传播奠定基础，可应用于绘画作品的艺术风格识别、检测、情感识别等不同领域。因此，如何更加有效地组织并管理艺术风格作品，使用户更加简便快捷访问艺术作品成为当前文化遗产数字化领域急需解决的问题[1]。

近年来，国内外图形工作者采用卷积神经网络(convolutional neural networks，CNN)、尺度不变特征变换(scale-invariant feature transform，SIFT)等方法对不同艺术风格绘画作品进行分类研究，成为计算机图形学领域的热点问题[2]。杨冰[3]利用风格绘画的艺术风格特性进行分类处理，对艺术风格描述符和显著性特征进行检测，提出了一种不同艺术风格绘画的分类方法；祝娟[1]结合稀疏编码算法，比较高低分辨率绘画作品提取的特征，选取其中更具有绘画风格的代表性特征，同时利用信息论理论提取图像的特征，最后采用Weka软件中的分类器成功地对绘画作品的风格进行分类；万翠兰[4]基于稀疏编码算法，分析了图像的特征基函数和稀疏系数，采用四阶统计量对图像数据进行高阶统计，实现了图像风格的识别和分类；肖志鹏等[5]提出基于卷积神经网络的绘画图像和分类方法，获得分类结果，并分析了卷积核大小、网络结构宽度、训练样本数量等对分类结果的影响；赵永威等[6]针对矢量量化编码的误差严重问题，提出了一种基于深度学习特征编码模型的图像分类算法，减小了编码误差；陈小娥和陈昭炯[7]针对摄影作品、国画、水彩画、素描、油画等5种艺术风格图像进行分类，采用多类SVM分类器以及逐层分类的思想实现了对5类艺术风格绘画的分类；BARAT和DUCOTTET[8]结合图像的艺术特征，提出采用CNN的方法，并利用欧氏距离度量作品之间的相似性，实现了不同图像风格的分类；CHU和 WU[9]选取漫画人脸图像作为研究对象，基于大规模基准测试数据，采用深度神经网络提取深层关联特征并检测人脸，对不同具有漫画风格的人脸图像进行分类和评估，获得较好分类结果；WILLIAMS和LI[10]提出了一种基于小波的CNN图像分类算法，将数据转换成小波域，在小波域空间进行分类以获得更高的精度；WANG等[11]针对高光谱图像进行分类，通过迭代滤波改变样本有限情况下的数据统计分布，并通过正交匹配追踪和支持向量机(support vector machine，SVM)对目标图像进行分类，提高了分类精度和效率。

基于CNN，SIFT等风格绘画分类方法存在模型复杂、耗时较多等问题，分类精度和分类效率有待提高。此外，艺术绘画风格种类众多，当绘画风格不同时，已有的分类方法可能失效。因此，对不同艺术风格绘画作品的分类研究还存在着精度不高、提高分类算法通用性等问题，仍然是图形学研究的难点。本文选取西方漫画、素描、油画、水彩画，以及国内烙画、水墨画、壁画具有代表性的绘画风格作为研究对象，针对7种不同绘画作品进行分类，获得最终的分类识别结果，图1显示了不同绘画风格的图像。

图像的信息熵表示图像中灰度、色彩分布的聚集特征所包含的信息量，反映了图像局部结构、色彩特征等信息量，可以用来作为图像质量的重要判断依据[12]。针对艺术风格作品的分类存在的精度不高等问题，本文提出一种基于信息熵的艺术风格绘画分类算法，在灰度信息熵的基础上，提出颜色熵、分块熵、轮廓熵3种不同的信息熵计算方法，并采用SVM对图像信息熵特征进行训练和分类。

图1 风格绘画实例

本文的主要工作为：①选取西方具有代表性的漫画、素描、油画、水彩画绘画作品，以及东方具有代表性的烙画、水墨画、壁画绘画作品作为研究对象，丰富不同艺术绘画风格的分类研究成果；②提出图像的颜色熵、分块熵、轮廓熵3种不同的信息熵计算方法，作为图像信息熵的计算依据。其中，颜色熵能反映图像的颜色特征，分块熵反映了图像的空间局部分布特征，轮廓熵反映了图像的边缘和结构特征；③针对训练样本集进行分类测试，通过采用不同核函数得出的分类效果进行验证，提高了查全率和查准率。

本文对艺术绘画风格分类研究，有利于用户鉴别不同艺术绘画作品的风格种类，分析不同绘画作品的风格特征；有利于艺术作品的保护和传承，在影视作品、广告宣传、数字娱乐、遗产保护等领域具有广泛应用。

1 系统实现框图

图2显示了本文的系统实现框图，首先搜集了漫画、素描、油画、水彩画、烙画、水墨画、壁画7种绘画艺术作品，每种艺术风格260幅图像，共1 820幅艺术风格图像构建数据集，作为训练和测试数据集；其次，对数据集进行去噪、裁剪等预处理：①设置3×3掩模算子，采用高斯滤波方法对图像进行去噪处理，消除噪声；②当目标图像的背景区域较多时，对图像进行裁剪，保留主体区域；③对图像进行规范化处理，通常将训练和测试数据集图像处理为512×512大小；接着，从绘画艺术作品中选取部分图像作为训练集，对不同风格作品进行特征提取，计算图像的颜色熵、分块熵和轮廓熵特征，合并后形成信息熵矩阵，并进行特征训练；再次，利用开源的SVM的软件包LIBSVM对训练集进行学习训练，得到艺术风格绘画分类模型；最后，对测试集中数据进行特征提取，计算图像的颜色熵、分块熵和轮廓熵特征，合并熵矩阵，并通过训练好的分类模型进行测试，得到最终的艺术风格绘画分类结果。

图2 系统实现框图

2 图像信息熵

图像的信息熵通常指图像灰度值的信息熵，即图像灰度的概率分布情况[12]。色彩是不同艺术风格图像的重要特征，仅仅通过图像灰度值进行信息熵计算不能满足分类要求，此外，图像的局部结构特征以及图像的轮廓特征对图像艺术风格分类也具有重要作用。因此，本文在获得灰度图像信息熵的基础上，分别通过图像的颜色值、局部灰度值、Contourlet变换系数值求取信息熵，即计算图像的颜色熵、分块熵和轮廓熵，用于本文信息熵的计算和艺术绘画风格分类。

2.1 颜色熵

不同艺术风格作品具有不同的色调，如素描画、水墨画以黑白色调为主，烙画以褐色色调为主，油画、壁画色彩丰富较为鲜艳，因此，在艺术风格图像分类识别时，颜色特征对不同绘画风格的鉴别起到了非常重要的作用。在图像的不同色彩模式中，LAB色彩模型是由亮度L和A，B色彩通道组成，是一种与设备无关的颜色模型，且色彩与亮度之间的关联性较小[13]，与HSV，RGB等色彩空间相比，在图像的色彩熵分析中具有色彩描述特征准确的优势，因此，本文基于 LAB颜色空间，计算图像的颜色熵。

颜色信息的分布具有一定的概率统计，与图像内容分布有关，同时与图像的色彩域有关，不同颜色的图像具有不同的色彩域。LAB颜色空间中，L通道表示亮度信息，A通道和B通道反映了图像的颜色信息，基于LAB颜色空间的颜色熵计算方式如下：

首先，将图像从RGB色彩空间转到LAB色彩空间[13]，分别对A，B通道求信息熵，表示图像的颜色域分布特征[14]，即

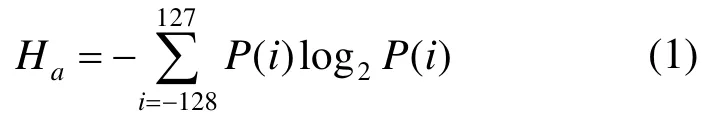
其中，P为图像A通道颜色值，式(1)可计算A通道的颜色信息熵Ha，通道B采用同样的方法计算。考虑到在不同的艺术图像中，2个颜色完全不同的图像，可能具有相同的信息熵，因此引入一个加权函数，设H为某幅图像的颜色直方图，采用冒泡排序方法将直方图H由小到大进行排序，完成排序后直方图灰度级的移动次数记为m。由于信息熵具有对称性，因此排序前后信息熵不会改变。加权函数f(x)定义为[15]

其中，m为直方图灰度级所移动的次数；z为直方图灰度级的总数。采用加权函数后，图像的颜色熵表示为

其中，Ha(x)为最终的A通道颜色熵，可以用同样的方法求取B通道颜色熵Hb(x)。

图3显示了不同艺术风格绘画的信息熵值，在实验中发现，色彩的丰富程度、色彩的明暗会影响最终的颜色熵，如水墨画以黑白色调为主，计算出的颜色熵就比较低；而颜色丰富多彩的油画、水彩画、壁画等，计算出的信息熵较大。因此，仅依靠图像的颜色熵还不能较好判断出艺术风格的分类结果。

2.2 分块熵

图像的空间分布是图像的一个重要特征，能表现出一幅图像的色彩分布和整体特性。不同的艺术风格绘画具有不同的空间分布，如一幅油画和一幅漫画相比较，其色彩、结构等空间分布有所不同。油画的立体感强，细节纹理丰富，图像中的局部区域有较丰富的纹理特征，富有立体和层次感。可以看出，细节纹理丰富的地方，像素值变化繁复，信息熵较高。此外，由于油画艺术效果色彩整体分布均匀，因此整体信息熵分布较均匀。漫画的构图中往往表现出着重点和非重点，如人物、中心物体等为画家着重表现的区域，在绘画时用较小笔刷注重细节的描述，而漫画中的背景等大面积着色相同的区域为非重点区域，画家在创作时采用较大笔刷，忽略细节信息，因此，漫画的整体信息熵分布不均匀，在细节较多的区域信息熵较高，在细节较少的地方信息熵较低。

图3 图像颜色熵用例

本文基于单元熵的思想[16]，在图像信息熵的计算过程中，提出采用分块信息熵方差来描述图像的整体空间分布特征。首先将图像分成n×n个方形小块，分别求取每一个小方块的信息熵，再求取一幅图像的所有小块信息熵的方差，方差越大则说明艺术风格图像的信息熵分布越不均匀，方差越小说明信息熵分布越均匀，信息熵方差计算为

其中，V为信息熵方差；Hi为小块信息熵；Hm为分块信息熵的均值；n为块数。

图像划分为小块后，相邻块之间存在着一定的关联，这种关联也体现了图像空间分布特征(图4)。因此，在信息熵计算过程中，为了表示小块之间的关联，提出分块联合熵的计算，对每一分块求其灰度值均值。同时，为了排除微小差异对结果造成的影响，对灰度均值以8为一个步长进行量化处理，并将相邻块灰度均值转化成离散的独立信源，其联合空间计算为[17]

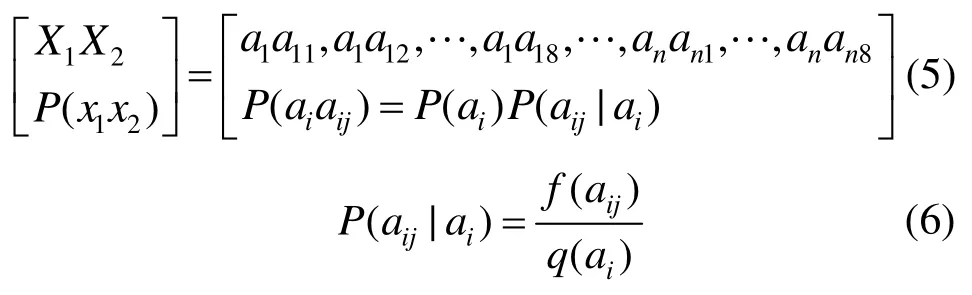
其中，X1X2为2个离散的独立信源，即2个分块；ai为分块的灰度均值；aij为与ai相邻块的灰度均值；P(x1x2)为分块之间的联合空间；f(aij)为块灰度均值为ai时，与ai相邻的块灰度均值为aij出现的频数；q(ai)为与ai相邻的块总数。分块联合熵计算为

其中，HL(X1X2)为分块联合熵；n为分块数。

图4 相邻块编号示意图

当一幅图像各块灰度均值分布越均匀、统一时，分块之间的联系越紧密，式(6)中相应的条件概率就越大，越大，随之分块联合熵H(X1X2)就越小。

为了验证图像的分块熵能够体现图像的空间分布特征，选取油画、漫画目标图像进行实验。在图像预处理过程中，通常将输入图像缩放为512×512 大小，采用 2n×2n(2≤n≤6)大小对图像进行分块，计算分块信息熵。当n=5时，图5中显示了当目标图像为油画和漫画时的信息熵结果。图5(a)显示目标图像为油画时，获得结果信息熵方差V=0.3，分块联合熵HL=0.6；图(b)显示目标图像为漫画时，获得结果V=7.1，HL=5.4。取不同n值进行实验，发现油画每个小块的信息熵都较大，分布比较均匀，并且分块信息熵方差较小，分块联合熵较小；而漫画的块信息熵大小不等，分布不均匀，且分块信息熵方差较大，分块联合熵也较大。从实验结果看出，艺术图像的分块熵可以表示一幅图像的整体和局部的信息分布情况，实验中考虑速度等经验值，n取值为5。

图5 图像分块熵计算

2.3 图像轮廓熵

艺术家在创作艺术风格绘画作品时，对图像轮廓的绘画并不相同，如漫画和烙画艺术作品，背景较为单一，然而注重勾勒对象的轮廓，因此，主体对象和背景之间对比度强烈，导致主体对象的轮廓细节比较明显；在油画艺术作品创作时，整体和局部往往呈现相同的色彩分布，不注重线条细节，忽略对主体细节边缘的勾勒；在水彩画艺术作品创作时，由于颜料的渗透性，导致边缘轮廓不明显；壁画创作时通常具有清晰明确的边缘特征，受到侵蚀、墙体脱落等原因可能造成图像轮廓的模糊；水墨画虽然不刻意的勾勒对象的轮廓，但是对象之间鲜明的墨色对比也让水墨画呈现出一定的轮廓特征；素描创作时往往通过背景以及明暗变化的阴影表现艺术特质，受到笔刷和铅笔线型的影响，其边缘轮廓较为粗糙。因此，轮廓熵对不同的艺术绘画风格具有重要作用，本文将轮廓熵作为图像信息熵的重要组成部分。

基于Contourlet变化思想[18]，本文提出图像轮廓信息熵的计算方法，描述图像的轮廓信息。Contourlet变化是Do和Vetterli等在继承小波多尺度分析思想的基础上，提出的一种非自适应方向多尺度图像轮廓捕捉方法。与二维Gabor变换、Cortex变换、二维小波变换、复数小波等其他多尺度多方向的几何图像表示方法相比，Contourlet变换能提供任意方向上的信息，具有多分辨率、局部定位、多方向性和各向异性等性质，更加灵活，有利于捕捉图像中的不同线条轮廓信息[19]。

图6显示了离散Contourlet变换的滤波器组结构图，输入的粗糙图像经过塔型方向滤波器组进行多层分解，可得到多尺度、多方向的子带图像。对于轮廓特征清晰的艺术风格图像，Contourlet系数变化大，信息分布复杂，因此获得的信息熵较高；对于轮廓特征不清晰的艺术风格图像，Contourlet系数变化平缓，信息分布较为均匀，因此信息熵较小。基于Do和Vetterli等实验结果表明，采用 3层拉普拉斯塔形分解(Laplacian pyramid，LP)、3级方向滤波器组(dirctional filter bank，DFB)的 Contourlet变换能取得较好的实验结果。本文计算图像的轮廓熵Hc时，对每一层LP的各方向系数求取信息熵均值，用3层轮廓熵来描述图像的轮廓特征[19]，即

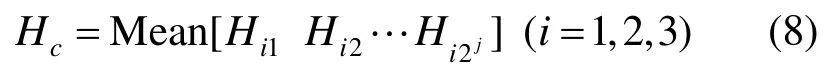
其中，Hi2j为对图像进行i层 LP分解后，DFB的Contourlet变换在第i层、第2j方向系数的信息熵。

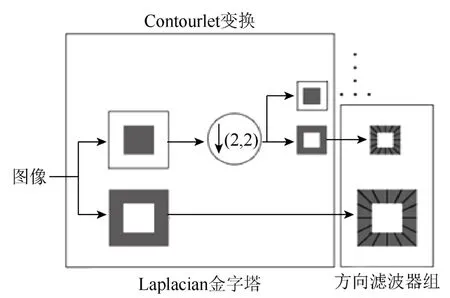
图6 Contourlet变换示意图[19]

为了验证艺术风格图像轮廓熵能描述图像的轮廓特征，选择轮廓特征不明显的油画和轮廓特征较明显的烙画进行实验分析。

图7显示了轮廓信息熵实验的用例图，将图7中的油画和烙画进行3级LP分解，每层8个方向的DFB滤波分解后，其轮廓熵结果见表1。

图7 图像轮廓熵计算用例

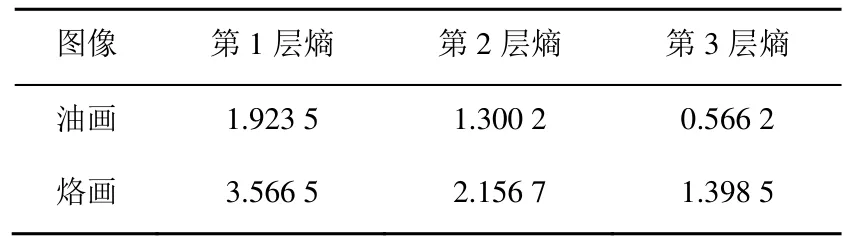
表1 图像轮廓熵

从表1实验数据可以看出，在不同层级熵值计算过程中，轮廓特征较不明显的油画轮廓熵值较小，而具有明显轮廓特征的烙画计算出的轮廓熵值较大。因此，轮廓熵能较好地描述出艺术图像的轮廓特征。基于颜色熵、分块熵、轮廓熵求取，对三者进行合并，获得最终的艺术风格图像信息熵，为最终的艺术风格图像分类奠定基础。

3 支持向量机

求取出艺术风格图像的信息熵后，需要对这些图像进行训练和分类。由于本文的不同种类风格画数据均是不超过300的小样本数据，因此本文采用在小规模数据的分类识别中有较好效果的SVM进行分类[20]。通过采用 SVM，对图像熵特征进行学习，并训练出风格画识别模型，进而对不同的艺术绘画风格进行分类。

3.1 核函数的选择

SVM 训练和测试过程中，核函数是关键组成部分，其通过把特征向量从低维空间映射到高维空间，使线性不可分问题转化成了线性可分，从而解决了多维特征空间的线性不可分问题，有效支持了数据集的分类和识别计算[20]。

在核函数的选择上，本文采用交叉验证(cross-validation)方法[21]，针对训练样本集，选取不同核函数，并对输入艺术风格图像进行分类效果验证，表2显示了核函数验证的准确率。

表2数据表明，采用Sigmoid核函数获得的准确率较低，使用RBF核函数获得的准确率较高，达到85%以上，可以取得较好的分类结果。由于RBF核函数更适用于特征维数少，非线性的情况，与本文数据量少、非线性分类一致，因此本文选取RBF核函数进行实验。

表2 Cross-Validation验证核函数准确率

3.2 参数设置

SVM模型有2个非常重要的参数c与Gamma，其中c表示对误差的宽容度，c越大表示误差概率越小，但容易出现过拟合的情况；c越小，容易出现欠拟合；c过大或过小，都会降低模型的泛化能力[22]。此外，RBF核函数中的Gamma参数决定了数据映射到新的特征空间后的分布，Gamma值越大，支持向量越少，分类速度越快，但精度可能会降低；反之，支持向量越多，分类速度较慢，精度将提高。

本文对艺术风格图像分类时，采用基于网格搜索(grid search)的SVM参数寻优方法对c和Gamma参数进行最优化选择。网格搜索是一种常用的寻找最优参数的算法，选择c和Gamma参数时，首先为参数设定一组候选值，然后从候选值中穷举所有参数组合，最后选择效果最优的那组参数作为最终参数设置值。

寻找最优参数实验对风格画样本集采用十折交叉验证的方法[22]。宽容度参数c取值cmin=–8，cmax=8，即在[2–8，28]范围进行穷举并找寻最优c值。RBF核参数Gamma用g表示，取值gmin=–8，gmax=8，即在[2–8，28]范围内进行穷举并寻找最优的g。SVM参数寻优方法参数选择结果如图8所示[23]。

图8 SVM参数选择结果图[23]

图8显示了采用不同参数实验样本分类准确率高低的情况，当取值为c=4，g=0.125时，准确率达到 82.8%，即达到最高值。因此，本文实验时，参数设置选取该组c和g值对艺术风格图像进行分类。

4 实验流程

本文实验基于LIBSVM开源数据包，通过SVM实现对不同艺术风格图像的训练和分类。实验流程如图9所示，实验步骤如下：

步骤1.从油画、素描等 7类风格画数据集中各随机选取100幅作为模型训练样本，分别求取其颜色熵、分块熵和轮廓熵特征。

步骤2.将提取的熵特征整合成一个[m×n](m表示训练样本；n表示样本特征)的数据集，并设置对应的标签集。

步骤3.将上述特征矩阵作为训练集，选择RBF核函数，利用 LIBSVM 对训练集进行学习训练，得到艺术风格图像的分类模型。

步骤4.选取油画、素描等7类风格画训练之后的图像作为测试样本，按照步骤1 和步骤2的过程提取待识别图像的特征向量，将其分别输入步骤3训练好的分类器中进行识别，得出识别结果以及识别正确率。

步骤5.对待识别的图像设置任意标签，投入风格画分类器，得出分类结果标签。

图9 实验流程图

5 实验结果及分析

5.1 查准率和查全率

本文所有实验在Windows 7，32位操作系统中进行，基于2.3 GHz AMD Turion II CPU，4 G内存，采用Matlab2016编程实现。本文针对漫画、素描、油画、水彩画、烙画、水墨画、壁画7种不同的艺术风格绘画进行实验，主要采用准确率和查全率对所提方法进行验证。实验训练集从数据集中选取每类风格画100幅，测试集从剩余数据集中随机选取每类艺术风格画进行测试。

表3显示了本文实验的分类准确率，从实验结果可以看出，油画、壁画和水彩画的分类准确率相对较高，漫画和水墨画的分类准确率相对较低，选取的350幅测试图像中，分类正确的一共有309幅，平均分类准确率为88.28%。烙画和油画风格特色明显且较其他风格画容易区别，因此识别正确率较高；而漫画的绘画风格较多，不同作者、不同内容，会使漫画作品的风格变化多样，有的漫画颜色丰富、内容多变，有的漫画颜色又比较单一、内容简单，因此漫画识别正确率较低，漫画风格也是风格绘画分类和识别的一个难点。

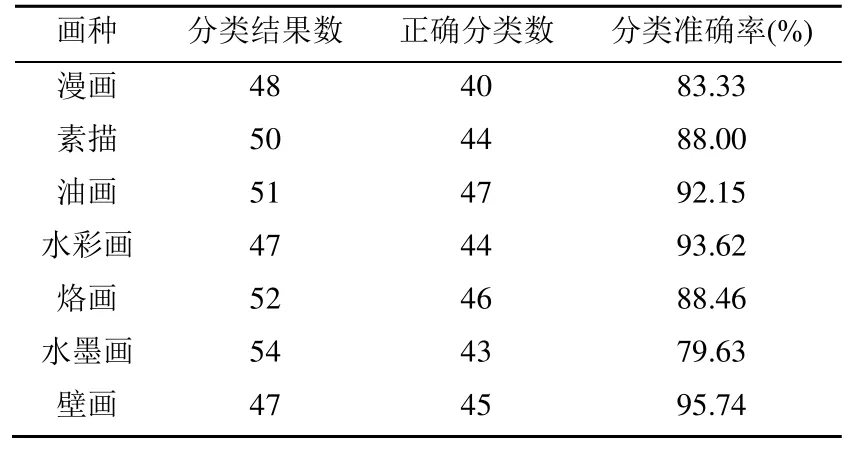
表3 分类查准率

表4显示了实验中不同风格绘画的查全率，烙画和油画的查全率相对较高，达到90%以上，这是因为烙画和油画识别准确率较高，不容易被错误识别为其他画种，因此查全率较高。漫画的查全率相对较低，只有80%，这是由于漫画识别准确率较低，容易被错误分类为其他画种，因此查全率偏低。查全率受分类准确率影响，准确率的提高有利于提升查全率。

表4 分类查全率

5.2 对比分析

文献[7]设计出一种针对摄影作品、国画、水彩画、素描、油画等5种艺术风格图像进行分类的系统。该系统通过设置多类SVM分类器，逐层分类，最终实现对 5类不同艺术风格画的分类，每一类SVM 分类器分别采用指定的图像特征实现各自的分类功能。

图0显示了文献[7]中多类二叉树分类系统，该分类系统采用3层4类SVM分类器，逐步实现对5类艺术风格画的分类，每种分类器利用不同的特征对指定的风格画从上至下逐层实现分类，其整体分类准确率为85.56%。本文算法对艺术绘画风格的分类准确率为88.28%，准确率有所提高。此外，文献[7]与本文都采用SVM分类器进行分类，包括训练和分类 2个过程，在最坏情况下，SVM 的算法时间复杂度为O(n3)[24]，其中n为样本数量，时间复杂度随着样本数量的扩大而增加。文献[7]通过分层方法对样本进行至少3次SVM计算，耗时较多；本文求取信息联合熵时，时间复杂度为O(n2)，并采用SVM对数据集进行1次训练和分类，减少了运算时间，当样本数量较大时，加速计算过程，提高了分类计算效率。

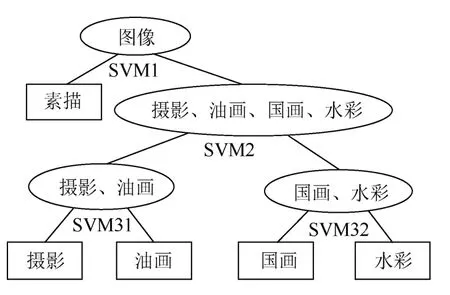
图10 不同艺术风格分类的SVM多类二叉树分类[7]

5.3 尺度不变性

图像熵是具有统计特性的图像特征，描述的是像素的空间分布特性，无论图像缩小还是放大，都不会影响图像像素点的分布特性。

本文对不同尺度的同一幅艺术风格图像进行测试，选取了烙画、油画、素描等艺术风格图像进行测试，图1显示了图像尺度分别为 512×512，256×256，128×128的图像实例，算法通过计算颜色熵、分块熵、轮廓熵对图像进行训练和测试。选取RBF核函数，实验参数选取c=4，g=0.125，经过对输入3幅不同尺度的图像进行实验，获得的实验结果为Ha=4.1，Hb=5.3，V=6.8，HL=5.9，三层轮廓熵分别为2.4，1.7，2.1，可以看出，图像尺度大小不会对信息熵造成影响，因此，测试结果显示不同尺度的图像具有相同分类，说明本文算法具有尺度不变性，为不同尺度艺术图像的分类识别提供了一种通用的计算方法，扩展了应用领域。

图11 不同尺度的图像

6 结束语

本文针对艺术风格图像分类算法进行研究，提出了一种基于信息熵的艺术风格绘画分类算法，算法将漫画、素描、油画、水彩画、烙画、水墨画、壁画7种具有代表性的艺术风格图像作为对象，求取颜色熵、分块熵、轮廓熵，合并为艺术风格图像的信息熵，采用SVM对不同艺术风格图像进行训练、测试和分类。在实验过程中，本文采用准确率和查全率对实验结果进行验证，实验结果表明本文算法能有效对艺术风格图像进行分类，与已有的方法相比，算法具有运算速度快、尺度不变性等优点，算法实验结果可应用于艺术作品分类识别、虚拟现实以及文化遗产保护等方面。在今后的工作中，将扩大数据集和艺术风格种类，同时加入对比度、饱和度、纹理等不同特征提高算法分类的准确性。