“三体对话”:协同学习观照下数学对话的新路径
2020-01-18蒋虹

【摘要】协同学习是一种通过对话实现同伴互助、教师辅导的教学策略。有效的数学对话是实现协同学习的必要条件。“三体对话”为数学对话研究提供了一条新路径,它立足于课堂教学,关注学生与现实世界的对话、与他人同伴的对话、与自我内心的对话,以期让深度协同学习真正发生。
【关键词】协同学习;数学对话;三体对话;现实世界;他人同伴;自我内心
【中图分类号】G623.2 【文献标志码】A 【文章编号】1005-6009(2020)81-0031-04
【作者简介】蒋虹,江苏省常州市武进区刘海粟小学(江苏常州,213161)教师,高级教师。
协同学习是一种通过对话实现同伴互助、教师辅导的教学策略。日本教育学家佐藤学认为它主要由三个要素组成:组织符合学科本质的学习、建立相互倾听的对话关系、提出有挑战性的问题并展开高层次的思考和探究。那么,如何使这三个要素有机融合呢?笔者认为,深入数学对话是一条重要的路径。教师在教学中可以设法构建一个立体空间,引导学生进行一种精神相遇的深入对话活动。
一、三体对话的内涵
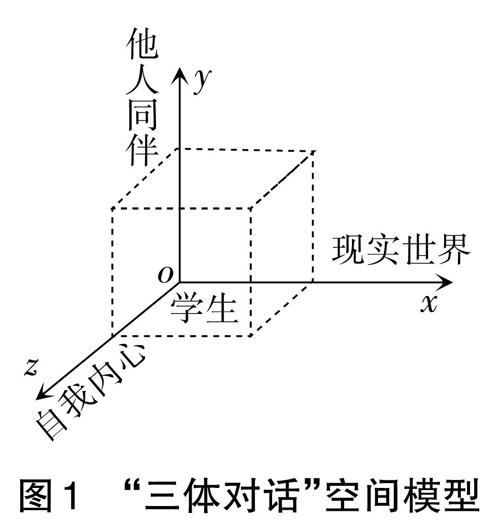
三维世界观认为:万物都在一定的空间存在。x、y、z是关键性的三个向度,决定着这个空间的大小与走向。学习对话同样如此,存在着特定的对话空间。三体对话是指教师引导学生分别与现实世界对话、与他人同伴对话、与自我内心对话。在这样三位一体的对话活动中,引导学生辩证地理解知识,系统地自主构建,从而使每个学生深度卷入学习之中。与现实世界对话、与他人同伴对话、与自我内心对话相当于x、y、z三个向度,稳定地构成立体的对话空间(如图1)。它具有三向性,向思维的宽度、广度和深度延展;它还具有均衡性,延展要平衡、融合、共生。三个向度发展得越和谐,对话空间就越宽广,认知活动就越深入。三体对话具有平等性、积极性、序列性、立体性,它的空间建构决定着学生学习的深度和品质。
二、三体对话在数学协同学习中的价值
(一)提升深度理解力
数学学习注重客观事实,数学知识的建构需要去情境、去形式、去个体,也就是在对话中要达到共性的理解。三体对话提供多种路径,让学生在讨论、交流、争辩和优化的过程中完成对知识的个性化处理和转换,从而达成意义建构。这个过程既能让学生对知识本质达到融会贯通,又能锻造他们的深度理解力。
(二)提升高阶思维力
数学思维力是一种数学化的思维方式。在三体对话中,有需要做出逻辑判断的问题情境,有能引发独立思考的学习过程,更有能形成思维矛盾冲突的交流机会,学生充分运用数学化思维去发现问题、提出问题、分析问题和解决问题。这个过程,在让学生的思维有机融入学习的同时,更能培养学生思维的深刻性、严谨性和批判性,使其向高阶思维转化。
(三)提升综合学习力
史宁中教授提出:数学核心素养是指具有数学基本特征的、适应个人终身发展和社会发展需要的人的思维品质与关键能力,也就是让学生会用数学的眼光观察世界,会用数学的思维思考世界,会用数学的语言表达世界。在三体对话中,学生积累了丰富的数学学习活动经验,感受智慧,实践智慧,从而生成智慧,培养综合学习力。
三、三体对话让协同学习真正发生
(一)x维:与现实世界对话——宽度决定量的积累
1.结构对话导引,让思維有轨可行。
数学思维是动态的过程。在对话伊始,要给学生提供结构化的对话导引,可以是显性的学习卡、学习任务、核心问题,也可以是隐性的、不同层级的探究活动。如此,才能让学生的数学思维有轨可行,能聚焦,能迁移。比如,教学苏教版五下《和与积的奇偶性》一课,笔者为学生提供了三个探究活动对话单:1号对话单让学生“研究两个非0自然数的和的奇偶性”;2号对话单让学生“模仿研究多个非0自然数的和的奇偶性”;3号对话单让学生“独立研究若干个非0自然数的积的奇偶性”。从研究目标和研究方式可以看出,这是三个不同层级的自主探究对话单。三个活动中举例的设计与结论的表达,从设定格式到半开放再到完全开放,让学生经历了探究方法类比迁移的过程,充分体现了“用结构学结构”的理念,学生从“他组织”走向“自组织”,其书面表达更是化无形为有形,真实刻画出了他们的思维轨迹。
2.个性对话表征,让思维有迹可循。
思维是人类特有的高级认知活动,具有内隐性、抽象性等特征,小学生的数学思维基本处于具体形象阶段或初级抽象阶段,发展水平极不均衡,类型、特点也有差异。因此,他们在与现实世界对话的过程中形成了丰富的、个性化的意义表征。教师适时鼓励学生把这些思维痕迹真实地呈现出来,将会为其接下来与他人同伴对话提供差异性的宝贵资源。比如,教学苏教版五上“解决问题的策略:列举”单元例2:南山中心小学举行小学生足球赛,有4支球队参加,分别是红队、黄队、绿队和蓝队。如果每两支球队比赛一场,一共要比赛多少场?学生利用文字、符号、图(图形、图画、图表等)、算式等不同的方式进行了思维的可视化表征,但他们的思维水平有一定的差异。大部分学生的思维需要借助较为具体形象的方式来演示,少部分学生的逻辑推理能力较强,能将生活中的实际情境转化为抽象的数学模型。这些不同的表征方式让学生与客观现实的对话思维跃然纸上,形成了充盈的再生资源。
(二)y维:与他人同伴对话——广度决定质的变化
1.逐层式路径推进。
语言是思维的外壳。在初级认知资源板块化呈现时,学生就要在教师的引领下,通过序列化的言语对话阐述自己的观点,倾听他人与同伴的想法,在对比中分享,在分享中质疑,在思辨中纠偏,在互补中完善,促使思维逐层深入。比如,教学苏教版三下《小数的初步认识》,学生在教师引导下,通过两个层次的对话建构小数“0.5”的本质意义。
第一层次:具象表示“你的0.5米”
师:怎样表示0.5米?
生1:画一条直线表示1米,将这条直线分
成2份,其中很小的一部分就是0.5米。
生2:我觉得这样不准确,很小的一部分可以是0.5米,也可以是0.4米。应该将整个线段平均分成10份,其中的5份才是0.5米。
生3:我也觉得应该平均分,不过我不是画线段,而是画一个长方形表示1米......
第二层次:抽象出0.5米的含义
师:虽然大家用不同的方式表示1米,但都能准确表示0.5米。这些方法有什么相同点?生4:虽然用不同的方式表示1米,但都是将它平均分成10份,都是取其中的5份,因而都可以用0.5米来表示。
透过学生、教师以及同伴之间的对话,不难发现,不同的学生呈现出了不同的思维表征水平,教师引导学生把自己的思考表达出来,并不断在分享、对话、沟通中求同存異,从而逐步走向抽象。可以说,与他人同伴深入对话,可以让学生的思维从零散走向结构、从肤浅走向深刻。
2.模式化思维融合。
从本质上来说,数学是在抽象、概括、模式化的过程中逐渐发展和丰富的,只有深入到“模型“”建模”的意义上,数学学习才是真正发生了。在三体对话中,正确理解概念或解决问题只是达成了一种短程目标。教师注重挖掘概念或问题的核心内涵,拓展其与外部世界的联系,建立包容性强的问题模型,将能真正促进学生的数学理解。比如,教学苏教版五下“列方程解决行程类问题”,学生很容易就能在对话中明晰:当货车的速度未知,而总路程已知时,可以利用“客车的路程+货车的路程=总路程“”速度和×时间=总路程”这些等量关系来列方程解决相遇问题。但这样的理解是浅层次的,数学对话不能就此停止。教师还可以给学生提供一组生活中的实际问题(挖隧道问题、购物问题、面积问题等),引导他们继续研究和对话。最后通过比较、抽象发现:只要已知两个部分的总和,求其中一个部分的量,就可以用“一部分量+另一部分量=总数”这个等量关系来列方程解决,而乘法的等量关系具有一定的特殊性。如此,就水到渠成地建构出了方程中加法等量关系的模型。
(三)z维:与自我内心对话——深度决定体的形成
1.与前我对话,完善现我。
与现实世界对话,基于“我”的视域掌握的信息可能是片面的、存在谬误的。与他人同伴对话,基于“我们”的视域掌握的信息可能是被动的、零碎的。因此,与自我内心对话的首要目标是内化统整,形成“现我”的系统知识网络。比如,苏教版四下“三角形、平行四边形和梯形”单元集中认识三种平面图形的特征,输出的信息量巨大,大部分学生概念模糊,甚至混乱不清。因此,在单元练习前,笔者让学生绘制思维导图。画思维导图是促进学生与自我内心对话的一种重要方式,能让其思维从混沌走向明朗,从中心朝着各个方向自由发散、自由表达。
2.与现我对话,指向未我。
苏联结构主义符号学的代表人物之一巴赫金说,对话是一个无限进行的过程,永远没有终点。在与自我内心对话的过程中形成“现我”的系统知识网络,具有开放性和衍生性。在它逐渐成熟的过程中,又会产生新的学习欲望,从而引发与现实世界对话的新需求。然后,又会引起第二次三体对话活动,这样立体循环的对话活动会触发学习向更深处进发。比如,教学苏教版五上《三角形的面积》一课,探究三角形的面积公式时,学生在教师引导下理解并构建出“把两个完全一样的三角形拼成一个平行四边形,根据平行四边形的面积公式推导出三角形的面积公式”这一观念。其实教师往往都容易忽略这一点,受到前一课“平行四边形转化成长方形”活动经验的直接影响,学生更倾向于“直接把三角形剪移,拼成一个长方形或平行四边形”这种操作性思维。所以,学生往往会产生这样的疑问:还可以通过什么方法把三角形转化成我们学过的图形?这就促使他们继续与客观世界对话,深入探索,从而发现更多方法(如图2)。这样的学习才是发生了真正的深度覆盖,培养了学生的立体思维。
佐藤学说,协同学习就像演奏一首交响乐,每一个人就像不同的乐器,发出不同的声音。当各种声音和谐地汇聚在一起,就奏出了一首动听的乐曲。三体对话就创造了这样一个对话空间,从此,深度协同学习就在这儿发生了。
