Modelling tree mortality across diameter classes using mixedeffects zero-inflated models

Yang Li·Xingang Kang·Qing Zhang·Weiwei Guo

Abstract The mortality of trees across diameter class model is a useful tool for predicting changes in stand structure.Mortality data commonly contain a large fraction of zeros and general discrete models thus show more errors.Based on the traditional Poisson model and the negative binomial model,different forms of zero-inflated and hurdle models were applied to spruce-fir mixed forests data to simulate the number of dead trees.By comparing the residuals and Vuong test statistics,the zero-inflated negative binomial model performed best.A random effect was added to improve the model accuracy;however,the mixed-effects zero-inflated model did not show increased advantages.According to the model principle,the zeroinflated negative binomial model was the most suitable,indicating that the‘‘0''events in this study,mainly from the sample‘‘0'',i.e.,the zero mortality data,are largely due to the limitations of the experimental design and sample selection.These results also show that the number of dead trees in the diameter class is positively correlated with the number of trees in that class and the mean stand diameter,and inversely related to class size,and slope and aspect of the site.

Keywords Tree mortality·Mixed forest·Zero-inflated model·Hurdle model·Mixed-effects

Introduction

Diameter distribution is one of the most important factors depicting stand properties(Bailey and Dell 1973),and directly affects the growth of trees and forest dynamics(Meng 2006),while the dynamics of the stand diameter structure are determined by the growth and mortality of the diameter classes.Mortality occurrences are classified as either regular or irregular(Lee 1971).Irregular mortalities are mainly due to human disturbances and to natural disasters which are difficult to predict;regular mortalities are caused by competition(Peet and Christensen 1987).Consistent with other research in this area,this study focused on regular mortality.

Forest mortality has a certain inherent randomness and a great deal of‘‘0''data exists which relates to mortality that has not yet occurred(Zhang et al.2014).In these circumstances, ordinary least-squares regression methods used to fit discrete data are not appropriate(Affleck 2006).Some studies have proposed a two-stage method to solve the‘‘0''data problem(Eid and Øyen 2003;Gonzalez et al.2004).The first step utilizes a logistical model to obtain the probability of the mortality occurrence to determine whether mortality has actually occurred,and the second step fits the mortality to the number of trees.However,the first step requires a probability threshold to determine whether stand mortality,for which there is currently not an accepted method(Zhang et al.2012).

Many research areas have begun using zero-inflated models and the hurdle models to address the excessive zero data problem and have achieved some success(Yin 2002;Carrivick et al.2003;Rose et al.2006;Rodrigues-Motta et al.2010).Random effects have been recently introduced to further improve the adaptability of the model(Hall 2000;Yau and Lee 2001;Tooze et al.2002).Relatively few of these studies are used in forestry applications and are mainly focused on forest regeneration(Flores et al.2006;Rathbun and Fei 2006;Li et al.2011;Crotteau et al.2014).In addition,stand mortality(Zhang et al.2014),cone production(Calama et al.2011),and plant cover classes(Herpigny and Gosselin 2015)are also involved.The zeroinflated and hurdle models showed significant advantages in dealing with excess‘‘0''data.

In this study,different counting models,including the Poisson,negative binomial,hurdle and zero-inflated models,were used to fit the data from spruce-fir mixed stands on permanent plots in Jilin Province to simulate the number of dead trees.The aim was to select an optimum model by comparing the results,and then adding random effects to improve model accuracy.Through this process,we hoped to provide a feasible method for studying mortality models.

Materials and methods

Study area

The Wangqing Jingouling Forest,located in the northeast of Jilin Province(130°10′,43°22′,)at altitudes of 300-1200 m,was the area for this study.It has a hilly topography with slopes of 5°-25°.The annual average temperature is 3.9°C with an accumulated temperature of 2144°C,an annual 600-700 mm rainfall and a growing season of 120 days.The soil is brown coniferous soil with a granular structure and moist,loose roots with an average thickness of 40 cm.The site is mainly overcut natural conifers and broadleaved species.The main species are Korean spruce(Picea koraiensis Nakai),Manchurian fir(Abies holophylla Maxim.),Korean pine(Pinus koraiensis Sieb.et Zucc.),Korean birch(Betula costata(Trautv.)Regel.),and Amur linden(Tilia amurensis Rupr.).Other species present include painted maple(Acer mono Maxim),Manchurian ash (Fraxinus mandschurica Rupr.), Manchurian walnut(Juglans mandshurica Maxim.),Amur cork(Phellodendron amurense Rupr.), white birch (Betula platyphylla Suk.), Manchurian striped maple (Acer tegmentosum Maxim.),and Ukurundu maple(Acer ukurunduense Trautv.et Mey.).

Data

Four spruce-fir permanent sample plots were used and data collected between 1978 and 2008.This region is dominated by a spruce-fir forest community,a virgin forest stand after selective cutting at a volume intensity two to three times above normal(30-50%)followed by 10 or 20 years of recovery.The stand volume is 100-200 m3ha-1(virgin forest is 350-400 m3ha-1),and the distribution is centered upon small-diameter wood(Gong et al.2010).The plots,established in 1978,are 0.5 ha(100 m×50 m).Slope and other site factors,as well as the individual tree measurements and locations of the trees with 2-or 3-year remeasurement intervals were recorded.Forty-nine sample groups at 2-year intervals were selected and the number of dead trees in each diameter class(trees/plot)were used as the dependent variable.

A summary of the stand variable statistics at establishment is in Table 1.The number of dead trees in each diameter class is in Fig.1.In Fig.2,‘‘0''data comprises a large proportion of the samples(approximately 80%).

Variable selection

Stand mortality depends mainly on density and site quality.In this study,twelve alternative variables are shown in Table 2.Variance inflation factors(VIF)＞5 indicate that the variables have high collinearity and should be rejected.Therefore,this study screened variables with VIF ＜5,and those that were significant as explanatory variables were included in the final model.

Poisson model

The simplest distribution for modeling counting data is the Poisson distribution(Affleck 2006)with a probability mass function(PMF)defined as:

where y represents the random variable of mortality counts,y=0,1,2…;X is a vector of independent variables;and β is a vector of the regression coefficient.Depending on the nature of the Poisson distribution, its expectation and variance are equal,and both are equal to λ,defined as:

Negative binomial model

The negative binomial model is the Poisson model with a discrete parameter introduced to describe the heterogeneity of overly discrete data with a PMF defined as:

Table 1 Summary statistics of stand variables by plots

Fig.1 Summary of mortality counts by diameter classes.Dot size represents the frequency

where Γ is the gamma function and θ represents introduced discrete parameters. In the negative binomial variance Var[Y|X ]=λ+θλ2，when θ →0,the negative binomial distribution converges to the Poisson distribution.

Hurdle Model

Fig.2 Frequency of diameter class mortality counts

To solve the problem of excessive‘‘0''data in real life,Mullahy(1986)proposed the hurdle model,for which the main premise is the division of the model into two parts.The first part simulates the zero probability of the data using logit,probit and other dichotomous models,and the second part utilizes positive counting models,such as the Poisson, negative binomial, and typical zero-truncated standard discrete distribution models.Its PMF is defined as:

Table 2 Modeling alternative variables

where p is the probability of an event taking‘‘0''and 0 ≤p ≤1.

Using the hurdle model in this study,part 1 selected common logit model,namely

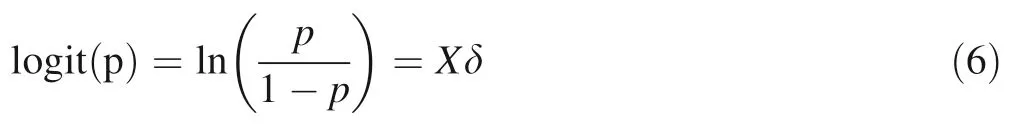
where δ is the parameter vector to be estimated.

In part 2,we selected the Poisson and negative binomial models for a comparative study,hereby referred to as the hurdle-Poisson(HP)and hurdle-NB(HNB)models.

Hurdle-Poisson model

Embedding the zero-truncated Poisson distribution expression into the hurdle model,we obtained the hurdle-Poisson(HP)model:

Hurdle-NB model

Similarly,embedding the zero-truncated negative binomial model into the hurdle model yielded the hurdle-NB(HNB)model:

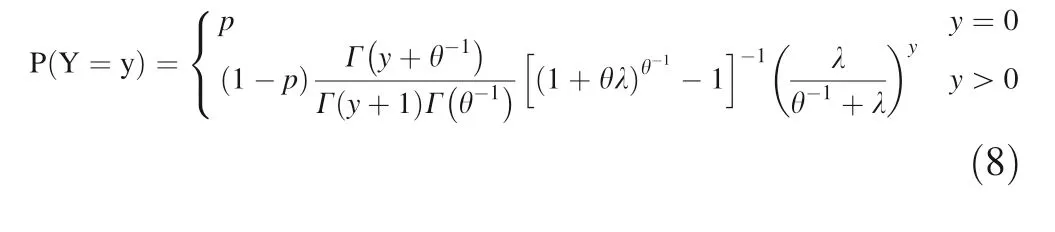
Zero-inflated model

Like the hurdle model, the zero-inflated model also evolved to fit discrete data but unlike the former model,the second part of the zero-inflated model is the complete discrete model,including the part that takes the value 0.In other words,in zero-inflated models,‘‘0''data occur from two main sources;first,the zero part of the logistical model that the event may never occur,and the second part,that it does not occur in discrete Poisson or negative binomial distribution theories.Its PMF is as follows:

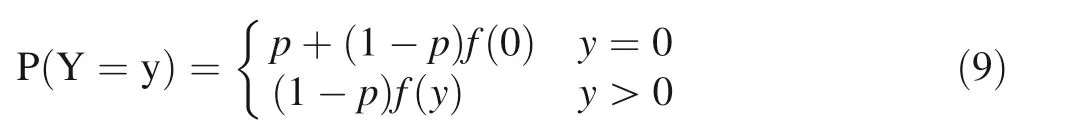
Similarly,the logit model was used in this study to combine the Poisson and negative binomial models into the zero-inflated model separately for comparison.

The zero-inflated Poisson (ZIP) PMF model is as follows:

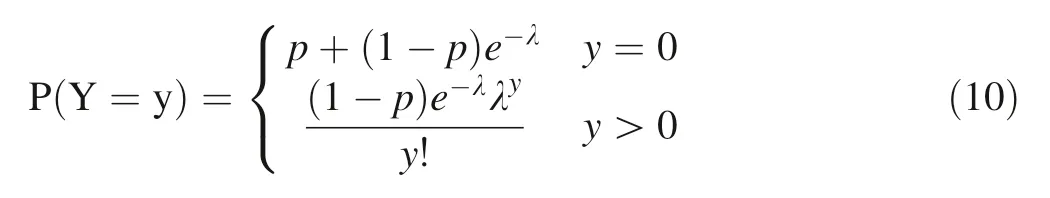
Introducing discrete parameters into the ZIP to become the zero-inflated negative binomial(ZINB)model yields a PMF as follows:

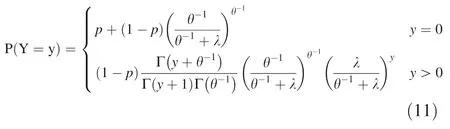
Random effects in this study,a plot-level random effects parameter was added to the optimal versions of the models described previously.The random effect parameter was defined as u ～N(0,v),where v is the variance.The unstructured covariance structure was used to describe the variance-covariance structure.

Model fitting

Parameters of the models were estimated via optimization of the likelihood function,i.e.,the maximum likelihood method.The likelihood function is defined as the probability of observing the responses of the dataset given the parameters,but it is regarded as a function of the parameters.These calculations were completed using the SAS NLMIXED procedure(Liu and Cela 2008).

Evaluation model

The Akaike information criterion (AIC) was used to compare model performances,and smaller AIC values indicated a better fit.

where logL is the log-likelihood,and k is the number of model parameters.

To determine whether differences between two models are significant, the likelihood ratio (LR) is usually employed for further testing and can also determine whether a discrete parameter is necessary.In this study,the standard negative binomial model was regarded as a nested model of the standard Poisson model with added discrete parameters(Zeng 2009).Similarly,the ZIP and ZINB,HP and HNB models also used the likelihood ratio test.

where logL1and logL2represent the log-likelihood of the two models,respectively.L1is the null model,i.e.,P,HP or ZIP,L2is their corresponding alternative model,i.e.,NB,HNB or ZINB.LR obeys Chi square distribution,LR ～χ2（1）.

Vuong metrics(Vuong 1989),a revised form of the likelihood ratio,were used for non-nested model tests and calculated as follows:

where Pj（Yi|Xi） is the prediction probability of the observed count for the ith case in the j-th model,¯m represents the average of mi

In counting data,the Vuong test aims to test whether systematic differences in the zero ratio exist between models one and two.If there is no difference between the two models,the estimation of the prediction probability should be close or the difference will be substantial.Vuong(1989)proved that V statistics obey the standard normal distribution limit and noted that statistics are bidirectional,i.e.,if V ＞1.96,model one is better than model two and vice versa if V ＜-1.96;if|V|＜1.96,it is not enough to prove that the two models are different.

Residual plots can be more intuitive when comparing the results of different model types.For counting models,because the residuals are heterogeneous, the Pearson residual(pr)value is often used:

To assess the adequacy of the models,an approximate χ2goodness-of-fit test was calculated using observed and predicted counts:

where#denotes the frequency of observations yiin count class k across the data set,and P r（yi=k）is the predicted probability that an observation belongs to count class k

Results

The statistical results show that most tree deaths occurred in diameter classes 6 and 8,and mortality varied from 0 to 13 in each plot during the survey period,with zero mortality was the most common. The mortality in the remaining classes decreased with diameter increase.After class 18,mortality was rare(Fig.2).

After evaluating the model parameters and excluding non-significant variables,the final fitting results for each model were tabulated(Tables 3 and 4).The parameter estimation results of the count part of the model,the mortality of the diameter class primarily associated with its diameter class size(dc),the number of trees in the diameter class(n),and the mean stand diameter(Dg),slope and aspect(SLC)are shown.In the count parts of these models,mortality was positively correlated with the number of trees in the diameter class and the mean stand diameter,indicating that higher numbers of trees and larger average diameters are correlated with higher mortality,i.e.,higher stand densities are correlated with higher mortalities.The mortality of the diameter class is inversely proportional to diameter class size;thus,as trees grow in diameter,less mortality occurs.In addition,the number of dead trees is also related to slope and aspect.In the zero parts of the hurdle and zero-inflated models,the zero event occurrence probability is negative in relation to the number of trees.Furthermore,higher numbers of trees are less prone to zero mortality,i.e.,more trees lead to stronger competition,and death is more likely to occur.Simultaneously,the zero event occurrence probability is also negative in relation to slope and aspect. This means that when the slope is southward,SLC is negative,and the greater the slope,the greater the mortality.When the slope is northward,SLC is positive,and the greater the slope,the less mortality.It is speculated that when the slope is facing south,the surface has abundant sunlight,and when the slope is large,soil erosion is large,which is not conducive to plant growth.While the shady slope lacks sunlight,the larger slope can give the plants more light.Therefore,the probability of tree mortality is reduced.

When the AIC values of each model were compared,the values of the negative binomial distribution model series(NB,HNB,ZINB)were smaller than that of the corresponding Poisson model series(P,HP,ZIP),i.e.,regardingcount models,the former is significantly better than the latter.The likelihood ratio test also produced the same result;the three pairs of the model likelihood ratios were 98.8,48.0,and 57.4(p ＜0.001),respectively,(Table 5).

Table 3 Parameter estimation and evaluation statistics of the standard Poisson model and negative binomial distribution model

Table 4 Parameter estimation and evaluation statistics of the Hurdle model and zero-inflated model

Comparing the Vuong test values for zero event predictions,the ZINB model was significantly superior to the HNB model(V=3.497,p=0.0002)and slightly better than the NB model(V=1.388,p=0.083).However,a comparison with the ordinary NB and HNB models did not demonstrate superiority (V=2.921, p=0.002). The Poisson series also yielded the same results.The ZIP model was superior to the HP model(V=2.867,p=0.002)and the general P model(V=2.353,p=0.009),and a comparison of the HP and P model showed no advantage(V=0.217,p=0.414).

As shown in Fig.3,transverse comparison shows the range of residuals in the negative binomial distribution series to be smaller than in the Poisson distribution series.By vertical contrast,residuals of the hurdle model converge and have the smallest range;however,on the whole,its predictive value is high.

In the model accuracy test,the HNB had the smallest χ2goodness-of-fit statistic,with a value of 12.66 compared with values of 12.96 and 15.02 for the NB and ZINB models,respectively.However,the χ2of the Poisson,ZIP and HP models are all more than 70,indicating that the difference is significant.Because the Poisson distribution is harsh,it is not suitable for the data structure with the simulated variance greater than the expectation,so the simulation result is poor.

In summary,of the six models ZINB performed better in fitting both the count and zero parts.The hurdle model residuals were in the minimum range was due to the modelmechanism in which zero part statistics are limited to only the structural‘‘0''and do not include the sample‘‘0''in the discrete model(Qin et al.2014).Therefore,in tree mortality studies,the probability statistics for zero events in the hurdle model are inferior to those in ordinary discrete models.As the zero-inflated models include the probability statistics of the above mentioned two zero data,the fitting effect was optimal.

Fig.3 Pearson residuals for fitting data

Table 5 Results of model evaluation statistics

Mortality across diameter classes research results suggest that‘‘0''data are mainly derived from the‘‘0''sample(He et al.2014),i.e.,the zero mortality data phenomenon is largely due to experimental design and sample selection.As mortality is an inevitable trend in the growth of forests,zero mortality is due to the limitation of objective experimental conditions and the occurrence of the mortality not being observed.

The optimal fixed effects model, the ZINB model,integrated the mixed effects.Random parameters were added to the count part intercept,the zero part intercept and the site condition variable SLC of ZINB to obtain ZINBmix1,ZINBmix2,and ZINBmix3,respectively.

The PMF of ZINB mixed-effect models are as follow:

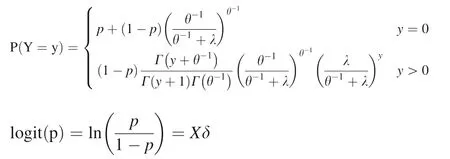
λ=eXβ

for ZINBmix1:

lnλ=β0+β1×dc+β2×n+β3×Dg+β4×SLC+u1logit（p）=δ1×n+δ2×SLC

for ZINBmix2:

lnλ=β0+β1×dc+β2×n+β3×Dg+β4×SLC logit（p）=δ1×n+δ2×SLC+u2

for ZINBmix3:

lnλ=β0+β1×dc+β2×n+β3×Dg+（β4+u3）×SLC logit（p）=δ1×n+δ2×SLC

where u1,u2,u3represent random effect parameters of the three models;u1,u2,u3～N(0,v),v is the variance.

Notably, ZINBmix2optimization could not be completed.The results of the other two mixed models are shown in Table 6.Both random effect parameters u1and u2were insignificant and did not show superiority compared with the ZINB model with V values of -0.626(P=0.532)and-0.802(P=0.423).Therefore,the final model selected was the fixed-effect ZINB model without random effects.

The final model is:

Table 6 Parameter estimation and evaluation statistics of the mixed models

Discussion and conclusion

The mortality of trees across diameter classes model has important forestry management significance.In this study,spruce-fir mixed stands were used to construct a diameter class mortality model using intervals of 2 years.Mortality was related to forest density,tree size and site.Specifically,the number of dead trees by diameter class was correlated with the number of trees in the diameter class and the mean stand diameter,i.e.,high numbers of trees and large mean diameters were correlated with higher incidences of mortality. This result is consistent with general forestry knowledge,as both mean stand diameter and number of trees represent stand density,wherein higher stand densities create more intense competition that mortality is higher.Mortality within the diameter class is inversely proportional to its size wherein larger trees are less prone to mortality. Generally, after competition during early growth,fewer large diameter trees exist and surviving trees enjoy a dominant position,which reduces mortality.In addition,the number of dead trees and slope factors were also correlated.

The Poisson distribution model was the simplest counting model,but its data requirements were too strict with little applicability.Therefore,a discrete parameter was added to yield the negative binomial model to explain,to some extent,the heterogeneity of the data.The hurdle model is based on the standard Poisson model wherein the negative binomial model is used to determine the probability of‘‘0''incidents and to provide a zero-truncated discrete model description data counting section. The hurdle model,therefore,is also known as a two-part model.

The zero-inflated model was also used to handle the practical problem of excessive‘‘0''data.This model differed from the hurdle model in that its discrete model section was not zero-truncated.However,the zero part of the discrete model also joined the zero probability judgment events.Therefore,the zero-inflated model‘‘0''has two sources,the structural‘‘0'',a dependent variable with direct access to the value zero,and the sample‘‘0'',a dependent variable due to its independent variable value of zero which includes stand density and other conditions that insignificantly result in the occurrence of tree mortality.In this study,the ZINB model performed the best of the six models,which suggested that‘‘0''events,mainly from the sample‘‘0'',were due to the experimental design and sample selection when‘‘0''mortality occurred.

The random effects of plots in the selected zero-inflated model were tested but the model did not improve significantly,which may have been due to insignificant differences in random factors between the plots.

Our study shows that the zero-inflated model,rather than the traditional counting model,fit excess‘‘0''data with some improvements.However,due to the strong randomness of forest mortality,the final model prediction was still somewhat unsatisfactory. Further studies considering additional factors and random effects are required.

In previous studies,the zero-inflated model was used mostly for plantations and performed well.This study attempts to apply this type of model to natural mixed forests.It also improves the precision of the model compared to the traditional Poisson model or the negative binomial model.In addition,this research takes mortality across diameter classes as the research object,so that the development of stand structure can be more accurately understood.At the same time,it also facilitates the study of the whole forest in combination with other growth models.

Due to limited data conditions,this study used 2-year intervals as survey samples,whereas practical applications may require additional studies at more intervals which require more extensive sample support.This study presents a feasible method for conducting this research and specific applications of these data require further investigation.