A basal area increment model for individual trees in mixed continuous cover forests in Iranian Caspian forests

Nishtman Hatami·Peter Lohmander·Mohammad Hadi Moayeri·Soleiman Mohammadi Limaei

Abstract The aim of this study was to develop and test a new basal area growth model in mixed species continuous cover forests in northern Iran.We analyzed 421 core samples from 6 main species in the forest area to develop our growth model.In each plot,we measured variables such as total tree height(m),diameter at breast height(DBH)(cm)and basal area of larger trees as cumulative basal areas of trees(GCUM)of DBH ＞5 cm.The empirical data were analyzed using regression analysis.There was a statistically significant nonlinear function between the annual basal area increment,as the dependent variable,and the basal area of the individual trees and competition as explanatory variables.Reference area from the largest trees,was circular plot with area of 0.1 ha.GCUM was estimated for trees of DBH ＞5 cm.Furthermore,we investigated the dependencies of diameter growth of different species on stand density at different levels of competition,and diameter development of individual trees through time.The results indicate that competition caused by larger neighborhood trees has a negative effect on growth.In addition,the maximum diameter increment is affected by competition level.Therefore,the maximum diameter increment of species occurs when the trees are about 35-40 cm in dense-forest(40 to 0 m2 per ha)and when the trees are about 60 to 70 cm in very dense forest(60 to 0 m2 per ha)which is more likely to Caspian natural forests with high level density due to uneven-aged composition of stands.

Keywords Individual-tree model·Iranian Caspian forests·Continuous cover forestry·Mixed stands·Uneven-aged management

Introduction

Iranian Caspian forests are mainly located on the northern slopes of the Alborz mountains.They are considered as high quality and commercial forests in the temperate broadleaf and mixed forests biome.The biodiversity is high in fauna and flora.There is mounting evidence of interest in uneven-aged and uneven-sized forests, due to their higher diversity, regarding multiple purposes (Pukkala et al.2009),and reducing the regeneration costs(Øyen et al.2011).Consequently,it is essential to develop forest growth for optimal forest management.Moreover,in order to gain more economical benefits and guaranteeing optimal sustainable management,forest management should be implemented based on empirical relevant growth models.Investigating and studying vegetative state, can help executive managers in planning and executing of projects(Delfan Abazari and Saghebtalebi 2007).Growth models reflect facts of forests in which expressed accurately the relationship between factors affecting growth and their interaction effects(Namiranian 2010).The adaptive growth models are used to forecast products and help in investigating different approaches to manage forests ahead.There are not uneven-aged growth models as prevalent as evenaged ones(Peng 2000)due to limited studies focusing on management of uneven-aged forests(Heshmatol Vaezin et al.2008)or rare relevant data(Shugart and Smith 1996).

Methods of growth modeling which are used for uneven-aged forests have been developed in many ways for both stand-level and individual tree methods(Burkhart 1990; Peng 2000). Notwithstanding that, stand-growth models are simple and robust to simulate the stand growth but they are not able to give details as much as individual tree growth models(Vanclay1994;Peng 2000;Heshmatol Vaezin et al.2008).Individual tree growth models,are more practical for uneven-aged forest by considering many factors and predictor variables.They are categorized into distance-dependent(Ek and Monserud 1974;Schu¨tz 2006;Kuehne et al.2013)where there are spatial locations and independent models (Botkin 1993;Pokharel and Dech 2012)which are not based on spatial locations.

Furthermore, individual tree growth models can be developed as basal area increment or diameter increment models (Vanclay 1994). There are a large number of studies about basal area growth models instead of the diameter growth models(Pienaar and Shiver 1984;Pienaar et al.1985),because,the basal area is directly associated with volume growth.

Although uneven-sized stands exist in Iran,a few growth models,based on the dynamic factors such as competition,have been presented so far.Bayat et al.(2013)developed an individual tree diameter increment model for major species in Gorazbon forest using 258 circular fixed plots.

Heshmatol Vaezin et al.(2008)estimated increment model for some species in the Caspian forests of Iran.Lohmander et al.(2017)estimated a new basal area increment and volume function for beech in Iranian Caspian forests.Mohammadi et al.(2017)developed a basal area growth model for individual trees in uneven-aged forests in northern part of Iran.In this paper,the purpose was to develop and test a new basal area growth function using prevailing biotic variables such as competition and tree size.

Competition index can be considered by summing up the Basal Area of Larger trees proportionate to the subject tree and it is called(BAL),(CI),(GCUM)in various references(Wykoffet al.1982;Schu¨tz 2006;Mohammed and Heinz 2011;Lohmander 2017).GCUM can be determined for a distance-independent,distance-dependent and individual tree data set(Schu¨tz 2006).Zhang et al.(2014)indicated that competition was more effective factor compared to climate change in forest dynamic factors like mortality,growth,and recruitment.

There are some differences in all previous studies in Iran compared to the present study.For instance,the differences could be such as ignoring the competition factor for larger neighbor trees(Heshmatol Vaezin et al.2008),difference in studied area and development of models(Bayat et al.2013;Mohammadi et al.2017).

The aim of this study was to develop a basal area increment model for individual trees using empirical data from the species including beech(Fagus orientalis Lipsky),hornbeam(Carpinus betulus L.),ironwood(Parrotia persica(DC)C.A.M.),maple(Acer velutinum Boiss),oak(Quercus castanifoli C.A.M.)and alder(Alnus subcordata C.A.M.)in Iranian Caspian forests.

Materials and methods

Study area

We collected data from Shast-Kalateh forest in district number one with an area of 1713 hectares,which is located in Golestan province,watershed of number 85 in northern Iran.The latitude ranges from 36°43′27′′to 36°48′06′′N and 54°21′26′′to 54°24′57′′E(Fig.1).The bedrock of this forest is lime and sand stone with altitude ranging from 100 to 1000 m.The forest is mixed-deciduous which has been established on brown forest soil with sandstone bedrock.It is mostly containing clay loam silty texture,and worn stones are spread around the region.The forest volume ranges between 150 and 300 m3ha-1. Tree industrial species in the study area include hornbeam,beech,oak,alder,ironwood and maple.The main species in this forest are hornbeam,ironwood and beech.Hornbeam and ironwood are located at altitudes lower than 700 ms and beech with other species located above the altitudes of 700 m.In this forest,there are two small communities of oak and Caucasian elm trees,which are located in the northeast and northwest of the forest area,respectively.The wych elm and alder species are only found in the Fagetum,and the linden is also seen in the lower part of this community rarely.The flora in this region is similar to the Southern Caucasus,the east of the Black Sea(Turkish territory)and central Europe's flora.The mean of tree density per hectare is equal to 211 and the canopy cover is about 75-85%.The climate of the region is Mediterranean warm and humid,with mean annual precipitation of about 562 mm.The lowest amount is in July and August(Parsakhoo et al.2017).

Growth model

To determine the diameter growth of the 6 main species of the forest area,we chose 140 circular plots according to theprevious(rectangular grid of 150×200-m)random-systematic inventory network.The plots were from an area of 0.1 hectare as an alternate among all network plots(rectangular grid of 300×400-m).

Fig.1 Map of study area

We used increment borer,to take 3-5 core samples,based on the diameter classes of each species. These samples were taken from witness trees in each of specified plot,which were the closest tree to the plot center and the largest tree in the plot.Then,we measured the last 10-year period diameter growth in according to Mayer's method.We extracted all samples from DBH of trees at the same direction to detract from likely errors and eliminate unwanted factors,such as the effect of the geographical aspects.We measured the total height(m)and DBH of the witness trees as well.

Afterwards,we analyzed 421 core samples from the plots and used them for modeling of basal area increment.The core samples were including 95 beech(Fagus orientalis Lipsky),106 hornbeam(Carpinus betulus L.),68 ironwood(Parrotia persica(DC)C.A.M.),67 maple(Acer velutinum Bioss.),51 oak(Quercus castanifolia C.A.M.)and 36 alder (Alnus subcordata C.A.M.). Descriptive statistics of trees across the plots is shown in(Table 1).

We developed a new basal area increment function for several hardwood species and competition situation in northern Iran.The model is based on theoretical principles of forest growth.The production theoretical motivation,details and mathematical principles of this function are developed by Lohmander(2017).The following functional form selected which is builds upon a mathematical background of a general dynamic function for the basal area of individual trees derived from a production theoretically motivated autonomous differential equation.

The differential equation is in Eq.(1):

The parameters can be estimated via this linear reformulation in Eq.(2):

The parameters were determined via regression analysis.There are three parameters:a ＞0，b＜0，g＜0 in Eq.(3):

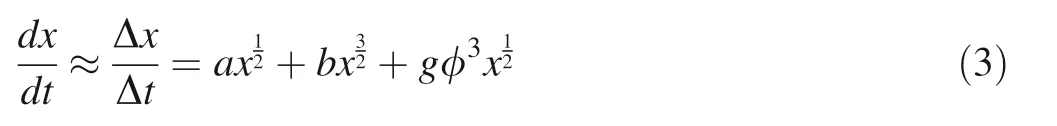
The parameters are all strongly significant and the graphs show that the developments of diameter and basal area are understandable and reasonable.In the regression analysis, Δt was 10 years and the values of x were approximations of the average x-values during the ten years.a is different for different species and affected bycompetition,x is the basal area cm2of a particular tree(P).Δt is a time interval and Δx is the change of x during Δt.φ is the total basal area(m2per ha)of trees larger than P.φ=φ（x）·≤0.φ is estimated from the 0.1 ha plot where P is located.The value of parameter a is a function of the species which P belongs to.

Table 1 Characteristics of the data set used for basal area increment modeling

The input variables used in growth modeling defined the affection of tree diameter,kind of species and competition.We used a joint function for total of the species,using dummy variables to consider each species influences.Furthermore,we used the variable of GCUM as an incremental competition factor,because it enables competition value for each diameter class.In this study,a reference area from the largest trees,was circular plot of 0.1 ha and GCUM specified at diameter class of 5 cm.In the later stages,we investigated dependency of diameter growth of different species on time and stand density at different levels of competition(in a less dense forest,dense forest and very dense forest),and also diameter development of individual trees through time.

Results

Growth model

The basal area increment function and the statistical estimation

The diameter varied from 5 to 160 cm for all species.The 10-year diameter growth was 0.6-10 cm for the most of trees.The following basal area increment function was estimated in Eq.(4).(Below the coefficients,the t-values are given.)

KF，KC，KQ，KPare the dummy variables,Ki∈ {0 ，1}∀i,representing different species.

If（KF=0，KC=0，KQ=0，KP=0）,then the function holds for maple and alder.The estimated coefficients were almost the same.There was no statistically significant difference between the coefficients between maple and alder.

If（KF=1，KC=0，KQ=0，KP=0）,then the function holds for beech.

If（KF=0，KC=1，KQ=0，KP=0）,then the function holds for hornbeam.

If（KF=0，KC=0，KQ=1，KP=0）,then the function holds for oak.

If（KF=0，KC=0，KQ=0，KP=1）,then the function holds for ironwood.

All estimated parameter values were significantly different from zero at the confidence level of 95%.Many of the parameters were determined with very high precision,which are shown by the t-values.The regression analysis also gave the following information as the analysis of residual diagrams shows that the suggested functional form fits the empirical data very well:R=0.975,R2=0.951,=0.950, F=1144. The standard deviation of the estimation is 112.055(with ten years'prediction)and the number of observations is 421.

Investigation of diameter increment models taken from basal area models and diameter development over time

We calculated the corresponding development of tree diameters,from the basal area development model,as the dynamic development of basal area calculated.Figure 2 shows that the diameter increment increases at the beginning during about 30 years. Then, the increment starts to decrease.Maximum diameter increment occurs very early when there is no competition.Alder and maple,grow in the same way.Alder,maple with oak grow faster and ironwood has the lowest diameter increment of the analyzed species.

Figure 3 shows that how the diameter develops in standing trees over time with assumption of no competition during 200 years.With competition,is obvious that growth would be lower.In this case,oak will be about 140 cm after 200 years.Maple,alder and beech will be about 120 cm.Hornbeam will be about 100 cm and ironwood will be about 40 cm.

Fig.2 Diameter increment as a function of time for different species without competition

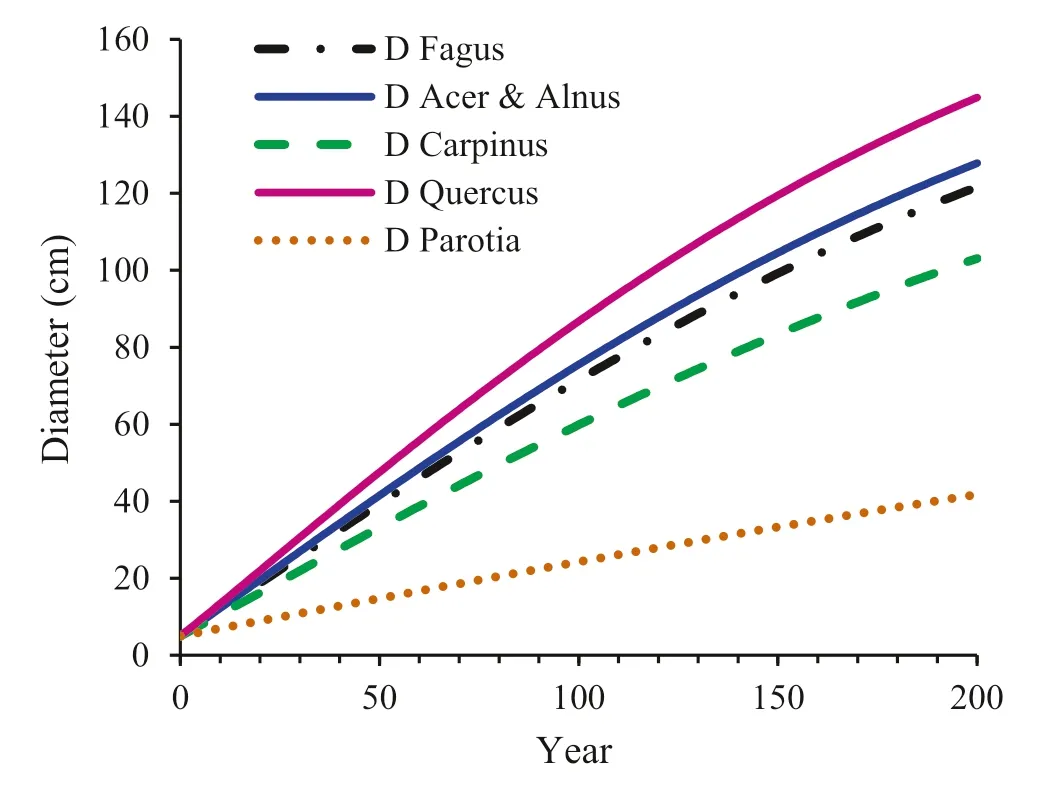
Fig.3 Diameter development as a function of time for different species without competition

Developing diameter growth models considering competition in three levels

We considered all of the species with three levels of competitions,to represent that how they will develop under such conditions.The competition,described as the sum of basal area of larger trees,φ,which is a decreasing function of the diameter of the particular tree,d.One example of such a competition function is found here:

Φ0denotes the total basal area,in case d is zero,φ=φ0.Φdis the derivative of φ with respect to d,in case φ ＞0.

Three examples of competition functions are found here:

In the first example,the total basal area is 20 square meters per hectare and the diameter of the largest tree is 120 cm:

In the second example,the total basal area is 40 square meters per hectare and the diameter of the largest tree is 120 cm:

And finally,in the third level of competition,the total basal area is 60 square meters per hectare and the diameter of the largest tree is 120 cm:

In the less-dense case,competition(φ)is assumed to be 20 m2per ha for small trees and 0 for big trees when diameter increases from 5 to 140 cm.Figure 4 show that how the diameter increment develops as a function of diameter in less-dense forest.In this competition level,the increment development is almost the same as without competition.

In the dense-forest case with much more competition,which is assumed from 40 to 0 m2per ha,growth is much lower for small trees.Figure 5 show that how the diameter increment develops as a function of diameter in dense forest.In this situation,the maximum diameter increment of different species occurs when the trees are about 35-40 cm.Ironwood has a very little growth during time and its growth is affected by competition in a high levels of competition.Regarding the growth model,in the dense level of competition,there was no growth for that and its growth went to zero.

In the third competition case,competition goes from 60 to 0 m2per ha.Figure 6 show that how the diameter increment develops as a function of diameter in very dense forest.In this case,small trees grow much less,because there is so much competition.It takes long time for small trees to grow big in this level of competition.Ironwood and hornbeam have not shown any growth in this case.In this competition level,diameter increment increases until about 60-70 cm of the trees,then begins to decrease.

Discussion

The Iranian uneven-aged forests have multipurpose benefits and services.Therefore,growth models need to be developed based on their specifications and characteristic.In this study,we predicted the basal area and diameter increment models for 6 different hardwood species.It can be practical for making decisions in different management subjects.

The basal area growth model is simulated using autonomous differential equation.All parameters obtained the expected signs and t-values indicated high precision.The differential equation has been found to work well with empirical data from Iran(Lohmander 2017).

Individual tree growth models may represent the whole stand,because each diameter class is demonstrated by one tree(Pukkala et al.2009).They can be used to simulate forest development in other similar forest regions.

In the particular growth model,competition was considered as the most important variable affecting on growth.This study investigated how the amount of growth was affected by competition.The result showed that competition is a negative factor for growth especially in a high level.Growth would be much less compared to when there is no competition especially for small trees,which are exposed to more competition.Total growth of all species appeared at a higher level when there was no competition(Fig.2).On the other hand,low competition seems to be essential for regeneration.The basal area increment model was adapted to assess relationship between various levels of density and increment measures(Figs.4,5,6).The models demonstrated that, alder (Alnus subcordata C.A.M.),maple(Acer velutinum Boiss.)and oak(Quercus castanifolia C.A.M.) can have faster diameter growth rather than the other species across the study conditions.It seems that finding optimal diameter is very important in order to make decisions regarding forest management and optimize desired goals.The goals could be timber production or ecological benefits.

Fig.4 Individual trees from six species in less dense forest.a Beech(Fagus orientalis Lipsky),b maple(Acer velutinum Boiss)and alder(Alnus subcordata C.A.M.),c hornbeam(Carpinus betulus L.),d oak(Quercus castanifoli C.A.M.),e ironwood(Parrotia persica(DC)C.A.M.)

Fig.5 Individual trees from five species in dense forest.a Beech(Fagus orientalis Lipsky),b maple(Acer velutinum Boiss)and alder(Alnus subcordata C.A.M.),c hornbeam(Carpinus betulus L.),d oak(Quercus castanifoli C.A.M.)

Fig.6 Individual trees from four species in very dense forest.a Beech(Fagus orientalis Lipsky),b maple(Acer velutinum Boiss)and alder(Alnus subcordata C.A.M.),c oak(Quercus castanifoli C.A.M.)

Cannell et al.(1984)indicated that competition among trees is one-sided or two-sided.In one-sided competition,larger trees are at a competitive advantage over small trees,but smaller neighbors have not any effect on the growth of larger trees.The basal area of larger trees has been found to be a helpful variable and is used to obtain one-sided competition in modeling tree growth generally(Wykoff1990).

It is quite possible that density is high in the beginning,but in the longtime,it is optimal to have lower density.Eventually,it is decided how much optimal density would be taken into account in uneven-aged forest management based on analytical numeric models.

The new model led to stable solutions,which is not always the case with other types of increment functions(Schu¨tz 2006).The estimated function in this analysis has similarities to the ones were determined by Bayat et al.(2013)and by Schu¨tz(2006)including competition,so that it makes sure the basal area increment is strongly positive only between zero and the maximum level.The differences are in numerical results and developing model using different species.The study showed that how competition in each level could influence on DBH or diameter increment.DBH increases over growing space of species(Kuehne et al.2013).The maximum diameter increment in each competition level varies from each other.It occurs when the trees are about 35-40 cm in dense-forest which is close to Schu¨tz's findings(2006)and about 60-70 cm in verydense level which is close to Bayat's findings(2013)in uneven-aged Caspian forests as it is expected to happen in natural forest with high level competition.The results were different between even-aged and clear-cut utilization in which the trees grow very fast in the beginning due to lacking competition for small trees (Lhotka 2017). It should be noted that,unlike Bayat et al.(2013),it is not easy to make the predicted relationship graphs between tree diameter(cm)and diameter increment(cm)for all the selected species in the same graph,because diameter was different for any studied species.Furthermore,it is easier to interpret the content of the graphs if they will be presented in separate figures.Unlike Mohammadi et al.(2017),the empirical model in this forest was considered only competition from larger trees and has led to different results.In Mohammadi et al.(2017)competitions were considered from all smaller and larger trees at distances ten meters or closer.The results showed a positive influence of competition on growth. The estimated results which were obtained in this study explained that,due to the plots with higher volume per hectare,and more competition,most likely they also had higher site index or better site productivity.

Conclusions

In the study,we developed a basal area growth model based on empirical data support.Now,it is possible to predict basal area of 6 different hardwood species under various levels of competition in mixed forest in Iran.The model can be very beneficial tool to optimize eligible targets in the forest management.The relevant targets could be determination of optimal stock level or limit diameter to assess the optimal present value from wood or non-wood and environmental benefits.There are a few growth models including all main species and such details.Since multiple agents affect growth models,it is suggested to consider various factors like climatic and physiographic factors.Developing growth models using more spatially details can lead to more in-depth results.

AcknowledgementsThe authors are grateful to Ministry of Science,Research and Technology of Iran for the scholarship to Nishtman Hatami to take a short time study in Sweden,which made it possible to perform this joint research in Umea,Sweden.

Conflict of interestThe authors declare that they have no conflict of interest.