基于深度学习方法的精神分裂症听觉稳态诱发电位分析
2020-01-18许飞飞应俊张立宁宋亚男谢惠敏陈广飞
许飞飞,应俊,张立宁,宋亚男,谢惠敏,陈广飞
解放军总医院 a. 生物医学工程研究室;b. 医疗大数据中心;c. 康复科,北京 100853
引言
精神分裂症是一种严重的精神疾患,其特点是思维、观点、情绪、语言、自我意识和行为出现扭曲,常见的症状包括幻听和妄想。世界人口中约0.3%~0.7%(约2100万人)患有精神分裂症,男女发病比例无明显差异[1]。精神分裂症患者平均预期寿命比平均值少10~25年,其背后的原因是患者较差的身体状态和较高的自杀率(约5%)[2-3]。临床上主要依靠于精神疾病诊断与统计手册(DSM-5)或国际疾病分类手册(ICD-10)中的标准并结合患者的实际症状做出相应诊断,但此时患者一般已经患病较长时间。精神分裂症病程多迁延并呈进行性发展,如果能够在患病早期准确诊断,并给予合理治疗,多数患者的病情是可以得到控制的,然而该疾病并没有任何客观的测试供作诊断[4]。
听觉稳态响应(Auditory Steady State Responses,ASSR)是由周期性刺激声音诱发,与刺激频率具有锁相性的脑电反应[5]。Kwon等[6]是最早研究精神分裂症患者40 Hz听觉稳态反应的,发现与正常对照者相比,精神分裂症患者在γ(30~200 Hz)频段内频谱能量显著减少,同时在刺激频率处的相位存在延迟和同步性减弱。Kirihara等[7]对188名正常人和234名精神分裂症患者的40 Hz听觉稳态反应分析,发现与正常人相比,精神分裂症患者在θ(4~8 Hz)频段内能量有所增加,在γ频段内能量较少。Thunel等[8]的一项关于精神分裂症患者40 Hz听觉稳态反应的meta分析指出40 Hz的听觉稳态反应可以作为精神分裂症的一个潜在生物标记物。
以往在精神分裂症方面的研究,主要采用传统的浅层机器学习算法进行研究。如李钢等[9]提取精神分裂症患者和健康对照者静息态脑电信号16导联上的6个频段的能量作为特征,采用多项式和径向核函数两种核函数的支持向量机对其进行分类。Santos-Mayo等[10]使用支持向量机和多层感知机对提取到的17个导联上20个特征(16个时域特征,4个频域特征)进行识别和分析。上述介绍的研究都是采用浅层机器学习算法,很难在有限的样本和计算单元来实现对复杂函数的逼近,泛化能力受到限制。
深度学习作为机器学习中一个崭新的分支,相比于传统浅层机器学习的方法,其优点在于它是基于多层特征学习的结构,可以从数据中自动学习输入数据从底层到高层的不同表示,对复杂分类问题具有较好的泛化能力。除了在图像和语音领域取得的显著成果,近年来,深度学习也被成功应用于生理信号的分析中,比如肌电、脑电和心电[11]。An等[12]针对基于运动想象的脑电数据分类,在所有被试的数据上,深度信念网络(Deep Belief Network,DBN)的分类准确率均要优于支持向量机(Support Vector Machines,SVM),表明深度信念网络是研究脑机接口的一个强有力的工具。尹虹毅[13]使用栈式自编码网络分析静息态下精神分裂症患者与正常对照者的脑电数据,提取五个不同频段的频谱能量作为特征,其模型最优分类准确率为74.57%。
综上所述,本文对精神分裂症患者与正常对照者40 Hz听觉稳态诱发数据采用DBN的算法建立分类模型,并且与传统的机器学习算法SVM的分类结果进行比较。在预测样本中利用准确率、灵敏度、特异度、ROC曲线评价模型的性能。
1 材料和方法
1.1 数据来源
本文所用数据均为医院采集的真实数据,共29名受试者,14名精神分裂症患者和15名正常对照者。14名精神分裂症患者包括7名男性和7名女性,均为右利手,年龄在21~40岁之间,平均年龄30.2岁。15名正常对照者包括11名男性和4名女性,均为右利手,年龄在22~36岁之间,平均年龄28.6岁,认知功能正常,听力正常,无已知神经学疾病。实验在隔声屏蔽室中完成,背景噪声强度小于15 dB(A),受试者被要求坐在舒适的椅子上,同时保持直立姿势,双耳给予声压强度为60 dB的40 Hz chrip刺激音。实验数据均采用清华神经工程实验室研发的Mipower脑电采集系统记录,采样频率为1000 Hz。以鼻尖为参考,所采集的样本数据都包括9个导联(F3、FZ、F4、C3、CZ、C4、P3、PZ、P4)上4~5 min的时域数据,导联位置按照国际惯例10~20系统。
1.2 脑电特征提取
1.2.1 能量与相位
对信号采用快速傅里叶变换获取其幅度谱和相位谱,根据幅度谱提取其在α波段(8~13 Hz)、β波段(14~30 Hz)和γ波段(31~50 Hz)3个频带的能量,根据相位谱提取其在刺激频率处(40 Hz)的相位,最终得到9个导联上27个能量特征和9个相位特征。
1.2.2 信噪比
SNR计算是通过检测信噪比计算相应频率处的信号功率谱Ps与周边频率处的平均功率谱Pn获得,见公式(1)。
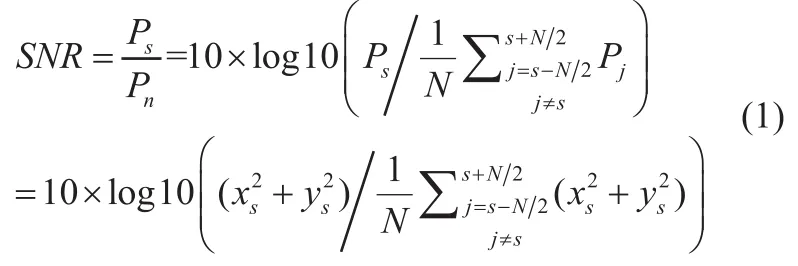
其中,xs表示时域信号FFT后,在响应频率处频谱的实部,ys表示频谱的虚部,xj表示在响应频率处周边的N点频谱的实部,yj表示在响应频率周边N点频谱的虚部,最终得到9个导联上9个SNR特征。
1.2.3 微分熵(Differential Entropy,DE)
DE扩展了香浓熵的概念并用于测量连续随机变量的复杂性。已经证明,对于一个固定长度的EEG信号,DE值等于某个频段内能量谱的对数值[14]。因为EEG数据低频能量高于高频能量,DE值具有在低频和高频能量之间鉴别脑电图模式的平衡能力,最终得到9个导联上27个DE特征。
由于深度学习网络模型训练需要大量样本,因此将每个受试者时域数据截取成多个时间样本,每个时域样本截取成长度为2 s的多个片段样本,处理后最终得到1025个精神分裂症患者的时间片段和1750个健康对照者的时间片段,最终每个片段共提取到72个特征(27+9+9+27=72)作为模型的输入模型的。
1.3 DBNs方法
DBNs是由多个受限玻尔兹曼机组成的[15]。一个受限玻尔兹曼机由一个可训练权值的马尔可夫随机场建立,其中所有节点被分为可见层和隐藏层。在玻尔兹曼机中,可见层表示模型的输入,而隐藏层表示从输入中提取得到的特征。
在受限玻尔兹曼机中,p(v,h;θ)是可见节点v与隐藏节点间h的联合分布。给定模型参数θ,p(v,h;θ)根据能量函数 E(v,h;θ)的定义如式 (2):
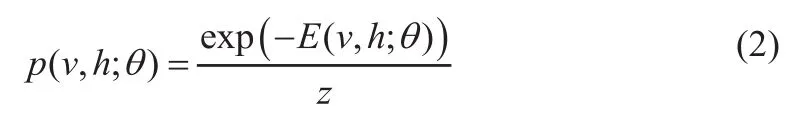
对于一个标准二值类型的玻尔兹曼机(伯努利-伯努利),能量函数定义如式(3):
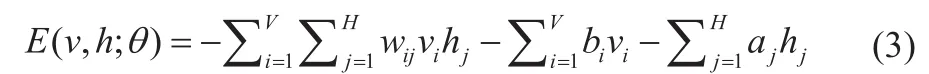
Z定义为归一化因子,计算公式为式(4):
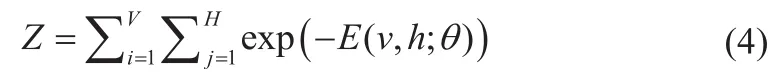
wij是可见单元vi与隐藏单元hj间的权重,V和H是对应可见单元与隐藏单元的数量,bi和aj均为偏倚权重。根据对数似然函数logp(v,h;θ)的梯度,训练迭代的权重wij更新公式如式(5):
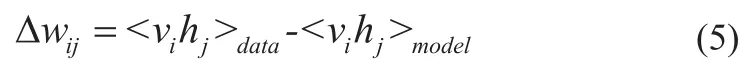

k表示分类的类别数,l=k表示输入向量的分类结果为k类,wik表示的是最后一层隐藏单元hi与第k类标签之间的权值。DBNs采用对比散度算法(Contrastive Divergence,CD)逐层训练每层RBM权值,CD算法核心思想是使用估计的概率分布与真实的概率分布之间的相对熵(Relative Entropy)的差异作为度量准则,在近似的概率分布差异度量函数上求解最小化作为训练参数的标准[16]。
本研究构建了一个包含两层隐藏单元的三层DBNs,见图1。其中,w0、w1、w2表示各层权值,先训练好第一个RBM1,然后将训练好的节点作为第二个RBM2的输入,训练第二个RBM2在两层RBM层训练完成之后,再使用反向传播算法对网络进行微调。
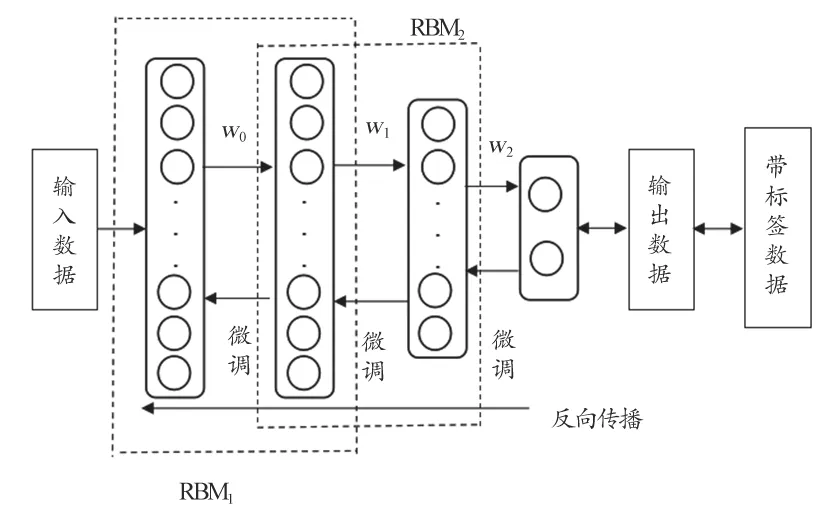
图1 DBNs训练流程图
1.4 支持向量机
支持向量机是根据统计学理论提出的一种机器学习方法,它集成了最大间隔超平面、Mercer核、凸二次规划和松弛变量等多项技术[17-19]。支持向量机是解决非线性分类、函数估计和密度估计等问题的一种有效方法,广泛应用于图像解释、数据挖掘、生物认证、生物技术调查和临床诊断等领域。关于支持向量机理论的具体解释,可以参考文献[18]。本研究使用支持向量机中最常用的三种核,分别是线性(linear)核、径向基函数(Radial Basis Function,RBF)核和sigmoid核。
2 结果
2.1 DBNs模型参数优化结果
本研究设计了一个含有两个隐藏层的三层深度信念网络模型,隐藏层的节点数量决定了深度信念网络模型的结构,因此隐藏层结构的选择对模型性能至关重要。本文研究了三种隐藏层结构在不同迭代次数下模型分类的准确率(图2)。从图2中可以观察到,无论哪种结构的隐藏层,其分类准确率总体都是随着迭代次数的增加而提高,当迭代次数过了200之后,准确率提高变得缓慢,当迭代次数到了300左右时,三种隐藏层结构模型的准确率基本不再提高了。比较三种隐藏层结构,可以明显看出隐藏层节点数为64-64时,无论迭代次数是多少,这个结构的深度信念网络模型的准确率都是最高的。迭代次数越大,深度信念网络模型的训练就越耗时,因此综合考虑时间成本,本研究最终选择了迭代次数为300,隐藏层节点数为64-64的深度信念网络模型。

图2 不同迭代次数和隐藏层节点下的精神分裂症和正常对照DBNs模型分类准确率
2.2 支持向量机模型参数优化结果
支持向量机有两个十分关键的参数C和γ。C为惩罚系数,表示的是模型对误差的宽容度,C越大表示模型越不能容忍出现误差,容易出现过拟合现象,相反C越小模型容易出现欠拟合。因此惩罚系数C过大或者过小会导致模型的泛化能力变差。γ是选择RBF作为核函数后自带的一个参数,γ的取值会影响RBF核函数里α的取值,α和γ的悬系如式(7)所示:

若γ取值过大,σ会很小,使得高斯分布又高又瘦,这样只会作用在支持向量附近,对于未知样本分类效果很差。对于SVM如何选择最优参数的问题,国际上并没有公认的统一的最好的方法,本研究选择最常用的网格搜索法(Grid Search)来确定模型的参数。
线性核函数、径向核函数和Sigmoid核函数建立的支持向量机模型的最优参数如表1所示,C取值为(2-5, 2-4, 2-3…24, 25),γ取值为(2-5, 2-4, 2-3… 24, 25)。

表1 SVM核函数的最优参数
2.3 模型识别结果与分析
本研究建立了SVM-linear、SVM-RBF、SVM-sigmoid和DBNs模型对精神分裂症患者和正常对照进行识别和分类,采用十折交叉验证的方式划分训练集与测试集,根据分类准确率、灵敏度、特异度和ROC这些指标对上述四个模型的分类结果进行评价和讨论。
表2给出了三种支持向量机算法和深度信念网络模型四项评价指标的结果,从表中看出DBNs模型在准确率、灵敏度和AUC三个指标上都高于三种支持向量机模型,而径向核函数支持向量机模型和线性核支持向量机模型灵敏度很高,但是它们的特异度均低于60%,说明模型存在过拟合,泛化能力不足。四种模型的ROC曲线如图3所示。不同于三种支持向量机模型,深度信念网络的灵敏度和特异度比较均衡,这证明DBNs更能学习到数据的本质特征,因此模型的泛化能力要远好于支持向量机。
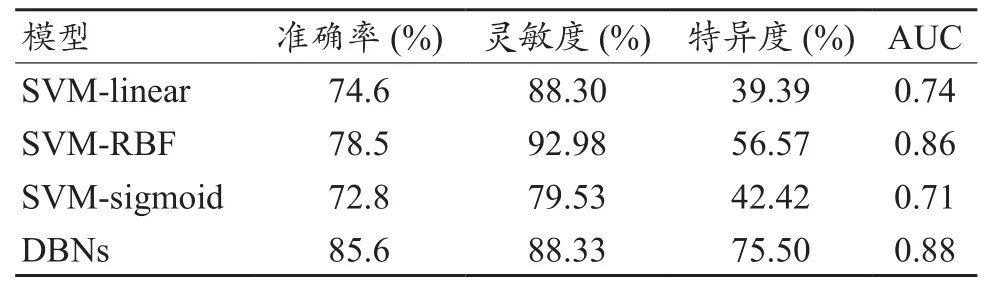
表2 SVM和DBNs模型的分类准确率、灵敏度、特异度和AUC值

图3 SVM-linear、SVM-RBF、SVM-sigmoid和DBNs模型的ROC曲线
SVM-linear、SVM-RBF、SVM-sigmoid三种支持向量机模型的分类准确率均未超过80%,且远低于深度信念网络模型的分类准确率,说明对于这个数据集,支持向量机算法建立的三种模型特征学习能力不如深度信念网络算法。三种支持向量机模型的灵敏度均较高,SVM-RBF甚至超过了深度信念网络模型,但是从模型特异度来看,SVM-linear、SVM-RBF、SVM-sigmoid三种模型的特度均未超过60%,这说明模型假阳性率较高,即很多正常对照者被误诊断为患有精神分裂症。反观深度信念网络,其特异度为75.50%,远高于三种支持向量机模型,这说明所建立的深度信念网络模型具有较强的泛化能力,具备一定的鉴别诊断能力。
3 讨论与结论
本研究基于机器学习算法基于脑电数据建立了精神分裂症患者与正常人的诊断模型。精神分裂症是一种十分严重的精神疾患,目前临床上是通过相应诊断量表以及医生的经验对其进行诊断,主要也是根据疾病的进展来对其进行诊断。本研究通过使用客观的脑电数据,使用深度学习算法建立数学模型对该疾病进行鉴别诊断,取得了较好的结果,可以为临床诊断提供一个参考,提高临床医生对精神分裂症的诊断能力以达到及时发现病情,给予及时的治疗。
本研究建立的四种精神分裂症模型均取得了不错的效果,但是还是存在一定的问题。三种支持向量机模型准确率均为70%多,也具备较高的灵敏度,但是其特异度均未超过60%,SVM-linear甚至只有30%多的特异度,这说明模型的假阳性率过高,容易把正常人误诊为精神分裂症患者,这样会消耗不必要的医疗资源,增加人们的医疗负担。相比于这三种支持向量机模型,DBNs模型的各项评价指标均很优秀,说明完全具备能力来对精神分裂症进行鉴别诊断。同时也说明DBNs这种深度学习算法能够学习到数据中蕴含的最本质的特征,证明DBNs比支持向量机具有更好的二分类能力。
虽然本文使用机器学习领域的算法对精神分裂症患者与正常人的脑电数据进行建模分析,从结果上来看确实取得了不错的成绩。然而机器学习是一种数据驱动的算法,样本量越大,所建立的模型才能更加接近真实世界。下一步工作可以尽可能多的采集数据,这样建立的模型才能有更好的泛化能力,来有效协助临床医生进行疾病的诊断。
