基于神经网络的马尾松人工林密度指数模型
2020-01-18刘光武王柯力
刘光武, 陈 晨, 王柯力
(1. 河南林业职业学院, 河南 洛阳471002; 2. 河南省南召县林业局, 河南 南召474650)
林分密度是评定林分内林木间拥挤程度的指标, 林分密度不仅影响木材的产量和质量[1], 还会影响林分稳定性[2]。 在影响林分生长的几个因素中, 林分密度是营林工作中能够有效控制的因子。 同时, 在建立林分生长收获模型时, 林分密度也是主要的考虑因素之一。 评定林分密度的常用指标中, Reineke的林分密度指数、 Beekhuis 的相对植距, 因为测定容易、 与年龄或立地条件关系不密切、 有实际经营意义等, 近年来被越来越多的人所采用[3-6]。 但是, Reineke 的林分密度指数、 Beekhuis 的相对植距存在过度依赖现存数学模型, 且对林分要求苛刻。 目前, 人工神经网络(ANN)在森林生长模型建模方面已有少量应用。 谢鹏芳等[7]对马尾松Pinus massoniana直径分布模型进行了研究, 认为神经网络建模具有较强的适应性。 廖世涛[8]对杉木Cunninghamia lanceolata人工林密度效应进行研究, 认为采用人工神经网络建立的密度效应模型科学合理, 预测精度优于以往传统模型。 马翔宇等[9]以白桦Betula platyphlla人工林为研究对象, 建立了单木生长神经网络模型。 金星姬等[10]以大兴安岭落叶松Larix gemelinii为研究对象建立了神经网络全林分生长模型。 陈晨等[11]对伏牛山栓皮栎Quercus variabilis天然次生林地位指数进行了研究, 认为神经网络建模技术具有过度拟合数据的缺点, 使用时必须定性定量相结合。 由于人工神经网络具有无限逼近非线性系统的能力, 且拟合速度快, 不依赖于现存的函数[12-13], 是目前解决复杂对象建模的最佳手段。 林分的生长过程是一个复杂的非线性过程, 适合采用人工神经网络来建模。 本研究以薄山林场马尾松人工林为研究对象, 采用人工神经网络建模技术建立密度指数ANN 模型, 并与Reineke的林分密度指数进行比较, 建立密度指数模型, 旨在为提高木材产量和质量, 实现马尾松人工林科学抚育经营提供参考。
1 研究地概况
研究区为河南省驻马店薄山林场, 薄山林场为伏牛山东段余脉浅山丘陵区, 地理坐标为32°36′~32°44′N, 113°50′~113°58′E。 山势平缓, 坡度为15°~30°, 海拔为150~250 m, 最高的山峰狠头寨高为430.5 m。 土壤为黄棕壤, 厚度为30~70 cm, pH 5~6, 为弱酸性土壤。 该林场位于中国南北气候过渡带, 水资源充足, 土壤肥沃湿润, 物种资源丰富。 该地区在气候地理区划中属亚热带向暖温带过渡区,年极端最高气温36.7°, 年极端最低气温-11.3°, 年均气温为15.5°, 年降水多分布在6-8 月, 年降水量为808~1 206 mm, 雨季明显。 林场土地总面积为6 017 hm2, 林业用地面积5 212 hm2, 马尾松人工林和栎类Quercus为该林场的主要树种。
2 研究方法
2.1 材料收集
于2015 年6-8 月进行外业调查, 并在2016 年6-8 月做了补充调查。 马尾松立地类型有下坡阴坡、下坡阳坡、 中坡阴坡、 中坡阳坡、 上坡阴坡、 上坡阳坡等6 个。 依据立地类型设置不同的标准地。 共设147 块标准地, 标准地面积为20 m × 30 m。 标准地主要林分调查因子特征: 年龄4~40 a, 平均胸径4.2~26.4 cm, 平均高3.4~22.7 m。 由年龄范围可知, 标准地林分年龄组涵盖了幼龄林、 中龄林、 近熟林、 成熟林等。 由立地类型、 龄组划分、 平均高分布等情况可知, 所选标准地具有代表性, 可以用来建立模型。 标准地数据见表1。
2.2 数据可行性分析
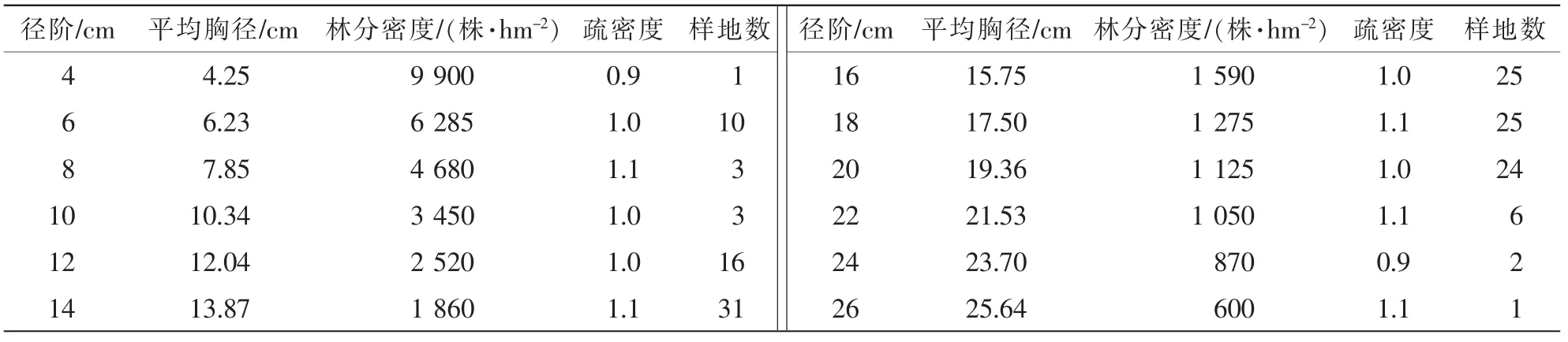
表1 林分密度统计结果Table 1 Statistical results of stand density
Reineke 的林分密度指数的建立是假设在完满立木度(疏密度为1.0 的林分), 未经间伐的同龄林中,林分单位面积株数与林分平均胸径遵从幂函数关系。 本研究所用标准地的马尾松为未经间伐的人工同龄纯林, 林分的郁闭度采用样点法测定, 依据郁闭度与疏密度的关系确定疏密度。 由表1 可以看出: 各组的平均疏密度近似为1.0, 因此可认为所用数据符合林分密度指数的完满立木度概念。
2.3 研究方法
2.3.1 林分密度指数法 林分密度指数(ISDI)是Reineke 在1933 年提出的, 指林分在标准平均胸径处应具有的单位面积株数。 Reineke 所采用标准平均胸径为25.4 cm, 中国林业生产中, 平均胸径通常取20 cm。 本研究采用拐点法确定标准平均胸径D0[13]。N=ISDI(Dg/D0)b;ISDI=N(D0/Dg)b。 其中:N为单位面积株数, 即林分密度(株·hm-2);Dg为林分平均胸径(cm);D0为标准平均胸径(cm);b为模型参数。
2.3.2 人工神经网络法 在Matlab 软件中, 应用nntool 工具箱, 以平均胸径Dg为输入变量, 以单位面积株数N 为输出变量, 建立林分密度指数的ANN 模型, 中间层为隐层,隐层神经元个数为待定的s个。 神经元个数的确定采用由少到多逐步训练的方式确定。 图1 中,w1s1(s=1, 2, 3…)为输入层节点Dg至隐层神经元的权值,b1s(s=1, 2, 3…)为隐层神经元的阈值, ①为输入值为1 的输入节点,w21s(s=1, 2,3…)为隐层至输出层节点N的权值,b2为输出层阈值,“S” 形符号表示神经元的传递函数为对数sigmoid 函数, 即Matlab 软件中的的logsig 函数。 “/” 符号表示神经元的传递函数为线性函数, 即Matlab 软件中的purelin 函数。
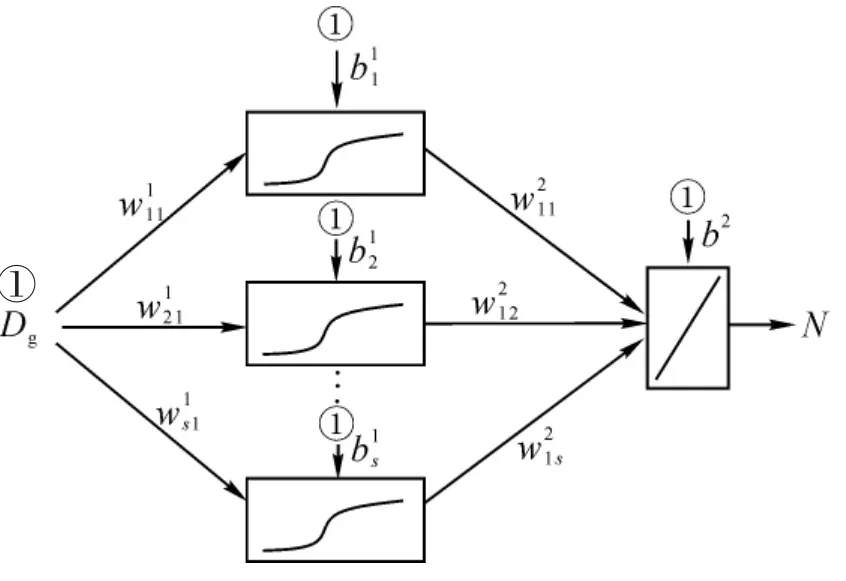
图1 林分密度指数ANN 模型Figure 1 ANN model of stand density index
3 结果与分析
3.1 林分密度指数参数求解
依据表1 数据, 经回归分析可得幂函数模型参数,N=677 9Dg-1.5163。 最大密度线斜率b=-1.516 3,与Reineke 研究的斜率-1.605 很接近。 图2 可知: 在林分发育初期, 林分密度随着林分平均胸径的增大而减小, 到后期, 随着平均胸径的增大, 林分密度逐渐趋于平缓或略微下降。 平均胸径14 cm 处为拐点, 因此马尾松人工林标准平均胸径D0为14 cm。 除第1 个点外, 实测值与拟合值拟合效果很好, 拟合精度为92.11%。t检验的P常数项为3.78 × 10-14, 线性项为7.87 × 10-10, 均小于0.05, 说明在回归方程中常数项与线性项均是显著的。 将b=-1.516 3,D0=14 cm 代入林分密度指数计算式:ISDI=N(14/Dg)-1.5163。
3.2 林分密度指数ANN 拟合结果
以平均胸径为输入变量, 以单位面积株数为输出变量, 依表1 数据为训练样本, 对图1 所建ANN模型, 在Matlab 系统里, 经反复训练, 同时结合林分密度随林分平均直径的变化规律, 即随着林分平均直径的增大, 林分密度曲线呈反“S” 型, 并逐渐趋于平稳, 最终确定薄山林场马尾松人工林密度指数模型为1∶2∶1 的ANN 模型, 模型拟合精度为92.57%, 均方误差为0.001 469 7, 所得ANN 模型共3层, 包括输入层1 个节点Dg, 隐层有2 个神经元, 输出层有1 个节点N。 将该模型命名为network2,network2 里面包含了所有的模型参数。 模型结构为:
式(1)~(3)中:Dg1、Dg2分别为隐层2 个神经元的输出值。 也可将模型简单写为:
拟合效果如图3, 林分密度随平均胸径的增大逐渐减小, 达14 cm 之后, 林分密度逐渐稳定, 这与Reineke 的林分密度指数曲线变化趋势是一致的。 在平均胸径达6 cm 之后, ANN 能很好地拟合林分密度随林分平均胸径的变化趋势, 但在林分发育初期, 却未能更好地拟合林分的生长发育过程, 这可能与数据的处理有关。 若能增加幼龄林组的数据, 可能会进一步提升拟合的精度。 在式(4)中, 当Dg为林分标准平均胸径D0时, 公式可写为:

由式(4)、 式(5)可得林分密度指数表达式:

将D0=14 cm 代入式(6)和式(7)可得:
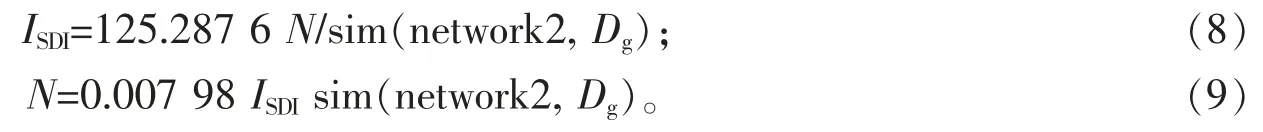
依据式(9)可绘制林分密度指数曲线簇(图4)。 当林分平均胸径相同时, 随着林分密度指数的增加,林分密度也在增加。 当林分密度相同时, 随着林分密度指数的增加, 林分的平均胸径在增大。
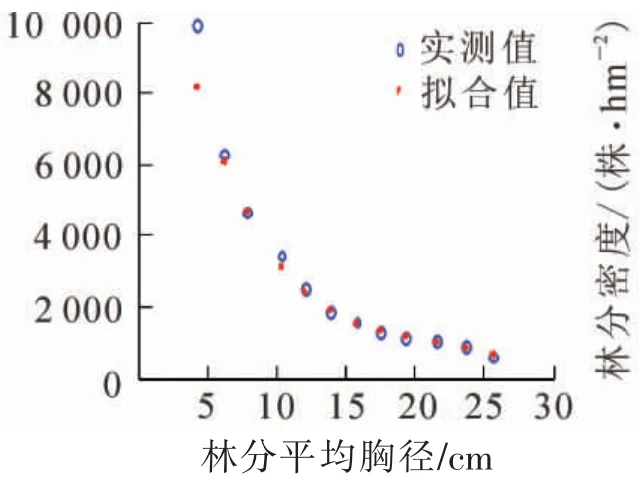
图3 林分密度ANN 拟合曲线Figure 3 ANN fitting curve of stand density
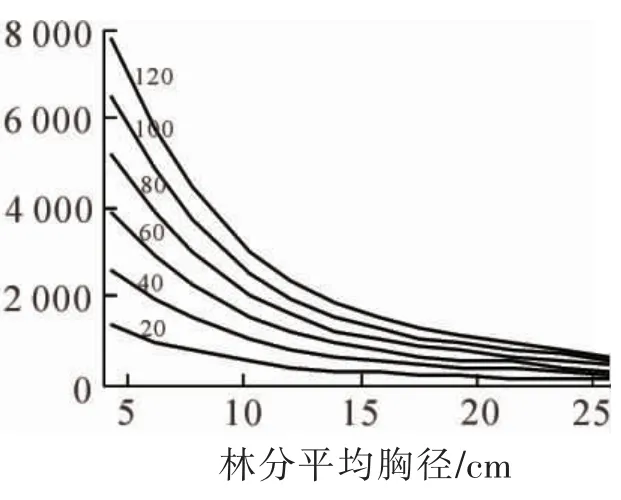
图4 林分密度指数曲线簇Figure 4 Stand density index cluster
4 结论与讨论
本研究数据来自不同立地类型、 不同龄级、 未经间伐的同龄林标准地, 经数据可行性分析, 所用标准地具有代表性, 运用标准地数据建立的Reineke 林分密度指数模型和人工神经网络密度指数模型能够准确反映林分密度的变化情况。 采用147 块标准地的林分密度—平均胸径数据, 以Reineke 的林分密度指数曲线为数学模型, 拟合林分株数密度与平均胸径的关系曲线。 经过回归分析, 求得最大密度线斜率b为-1.516 3, 模型精度为92.11%,t检验结果显著。 用拐点法求得马尾松标准平均胸径为14 cm, 林分密度与平均胸径的关系为N=6 779Dg-1.5163。 采用147 块标准地的林分密度—平均胸径数据, 以林分平均胸径为输入向量, 以林分密度为输出向量, 构建了人工神经网络密度指数模型, 结构为1∶2∶1。 人工神经网络密度指数模型简写为N=sim(network2,Dg), 模型拟合精度为92.57%, 均方误差为0.001 469 7。 模型精度及均方误差检验结果表明: 采用标准地数据所建立的人工神经网络林分密度指数模型精度高, 能够客观反映该地区林分密度变化情况。
人工神经网络建模技术与Reineke 的林分密度指数模型拟合精度均达92%以上, 都有较好的拟合效果。 与Reineke 的林分密度指数曲线相比, 人工神经网络密度指数模型具有不依赖于现存数学函数, 建模简单、 拟合精度高等优势, 在幼龄林组数据较少的情况下, 人工神经网络具有更好的拟合效果。Reineke 林分密度指数模型要求林分为未经间伐的同龄林且平均疏密度近似为1.0, 相对于Reineke 的林分密度指数, 人工神经网络对林分要求不高, 适用范围更宽。 2 种方法在拟合株数密度随林分平均胸径的变化趋势时, 幼龄林组拟合效果都不理想, 这与幼龄林组数据数量有关, 后期研究需增加幼龄林的数量, 进一步提高林分密度指数精度。
