倾斜岩面桩桩端竖向承载力计算方法
2020-01-18孙义舟童建富齐添孙宏磊蔡袁强
孙义舟,童建富,齐添,孙宏磊,蔡袁强
(1.浙江大学滨海和城市岩土工程研究中心,浙江杭州,310058;2.浙江金瑞建筑设计院有限公司,浙江杭州,310003;3.广州环保投资集团有限公司,广东广州,510330)
随着我国基础设施建设的全面开展,许多公路需要在山区修建。山区岩体状况复杂,许多桩基需要修建在倾斜的基岩岩面上,按照水平岩层分布进行设计比较危险,而增大嵌入比则会增大工程造价,同时给施工带来困难。对于嵌岩桩而言,桩端承载是其主要承载形式,因此,对倾斜岩面桩竖向桩端承载能力的评价与破坏机理的分析对工程建设有着重要意义。针对倾斜岩面嵌岩桩承载特性,国内外许多学者从不同方面展开了试验研究和理论分析。陈帝江[1]从理论分析角度对比研究了平坡桩基与斜坡桩基竖向承载机理的异同,并利用有限元软件进行了数值模拟。葛嘉诚等[2]利用克里格插值法对贵州某峡谷区斜坡基岩嵌岩桩进行空间分析,认为斜坡嵌岩桩的承载性能受嵌入度和基岩倾角影响。上述研究成果对倾斜岩面嵌岩桩的承载机理进行了定性分析,但具体理论和数值定量求解还尚未完善,因此,一些学者通过数学推导建立理论框架,对斜坡桩基承载机理进行深入分析。杨明辉等[3]采用幂级数解得到了斜坡桩的内力与位移分析方法。张洪波[4]研究了陡坡桥梁桩基的承载机理及荷载竖向传递机理。程刘勇等[5]总结了斜坡桩基竖向极限承载力的变化规律及其影响因素。MUTHUKKUMARAN等[6]通过室内模型试验研究了斜坡地基中单桩水平受荷的承载机理。赵明华等[7-8]揭示了考虑陡坡效应和嵌固深度效应的高陡坡桩柱式桥墩的承载机理并提出适用于工程的简化计算方法,在此基础上,杨超炜等[9]推导了具有“P-Δ”效应的陡坡双桩结构分析方法。为更清晰表述破坏的开展和应力应变关系,应用滑移线场理论求解斜坡嵌岩桩竖向承载力和承载机理是一种十分重要的手段。SERRANO等[10]引入瞬时内摩擦角,提出了基于滑移线场Riemann常量和Hoek-Brown非线性破坏准则[11]的嵌岩桩荷载系数。SERRANO等[12]将该方法与FLAC软件数值分析结果进行了对比。倾斜岩面桩基竖向承载机理和承载力计算的研究多针对数值模拟和试验研究方面,而利用滑移线场理论求解是一种概念清晰且直观的方式,有必要对此开展研究。本文作者根据水平岩面桩基滑移线求解理论[10],基于Hoek-Brown强度准则[11]和Meyerhof塑性理论[13],建立倾斜岩面桩桩端竖向承载模型,研究岩面倾角、桩嵌入比等因素对桩端承载力的影响,总结了倾斜岩面桩基桩端竖向承载力计算方法,以期为相关工程设计和理论研究提供参考。
1 计算模型与假设
由于岩面倾斜导致的桩侧岩体非对称分布,缺失岩体部分的桩前区域首先发生破坏,从而使得倾斜岩面桩极限承载力由单侧破坏标准来确定,破坏模型如图1所示,其中,η为岩面倾斜角度;α为滑动破坏面与水平面夹角,转角取逆时针为正;σv为上覆压力;HS为桩在土体中长度;HR为桩端嵌入岩体的深度;B为桩径。
根据MEYERHOF[13]提出的基础破坏模型和理想塑性理论,首先建立直径为B的桩嵌入倾斜岩面的平面应变分析模型。嵌入比其中,为桩前一侧嵌入深度。采用文献[10]中方法对带星号参数进行量纲一化,用不带星号的符号表示。
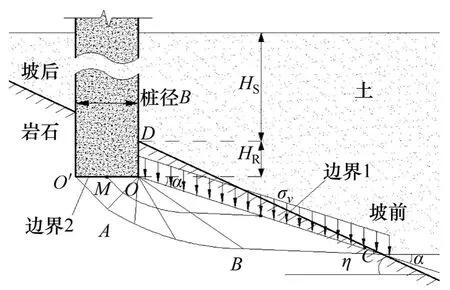
图1 破坏状态示意图Fig.1 Schematic graph of state of destruction
1.1 基本假设与破坏标准
1.1.1 基本假设
采用水平岩面桩基滑移线求解理论[10]假设:
1)计算采用平面应变假定;
2)岩体无黏聚力,均质且各向同性,视岩体为遵循Hoek-Brown准则的C-φ材料;当应力达到Hoek-Brown的强度标准时,判定岩体破坏,达到极限承载力,并假定岩体的变形不经历应变硬化过程;
3)破坏区域假设,根据MEYERHOF[13]提出的滑移线场确定桩端破坏区域;
4)滑移线场假设,应力和应变的滑移线场相同。
1.1.2 Hoek-Brown强度准则
Hoek-Brown强度准则[11]是一种用于研究岩体力学特性十分有效的经验准则,其表达式如下:
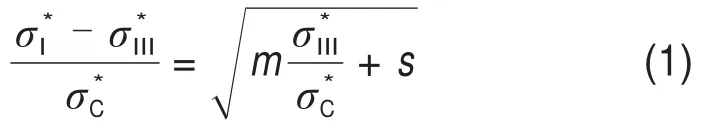
式中:为大主应力;为小主应力;σC为完整岩体的无侧限抗压强度;m和s为Hoek-Brown理论的岩石特性参数,分别代表岩体的软硬程度和破碎程度,可通过岩石类型m0和地质力学指数R或Hoek-Brown理论(1997版)的GSI指数[14]得到:
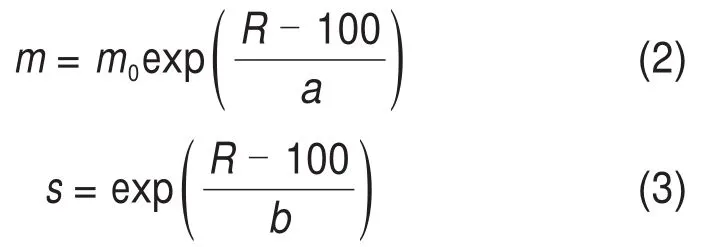
根据Hoek-Brown理论[14],当天然岩体未扰动时,a=28,b=9。
1.2 应力参数与瞬时内摩擦角
根据SERRANO等[15]提出的简化过程,采用平均应力p*和应力圆半径q*替代和可得
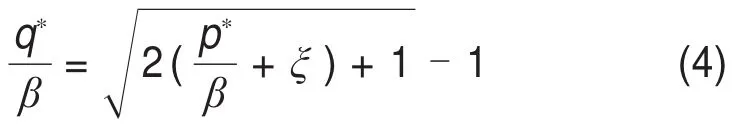
式中:β为强度模量,ξ为岩石的抗拉强度,。
为简化表达Hoek-Brown准则,对p*和q*进行量纲一化,式(4)可以写成
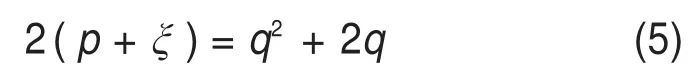
根据SERRANO等[15]定义岩石瞬时内摩擦角ρ为
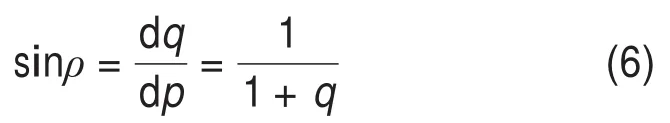
量纲一化参数q和p可采用瞬时内摩擦角表示:
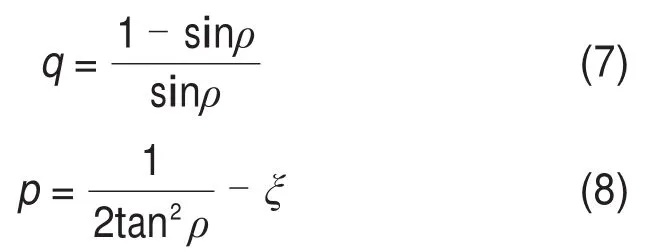
在应力坐标系中,量纲一的Mohr应力圆坐标可表示为瞬时内摩擦角ρ的函数:
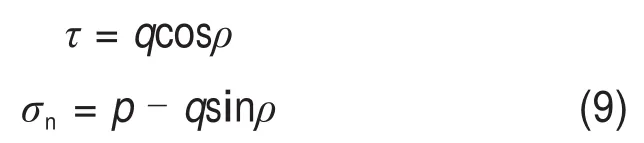
根据上述Mohr应力圆坐标表示形式,瞬时内摩擦角可表示为

1.3 计算方法
1.3.1 计算模型
在平面应变假设下,极限承载力σh垂直于作用桩底面(边界2),滑动面(边界1)与水平面夹角定义为角度α,桩端应力关系如图2所示。
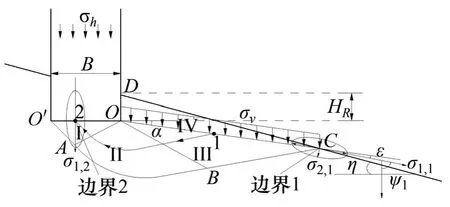
图2 滑移线场的应力关系示意图Fig.2 Schematic graph of stress relation of slip line field
1.3.2 假定滑动面
为方便分析,假定滑动面倾角α为已知,以覆盖层压力hm为计算的切入点,首先计算OCD三角形区域的质量W*:
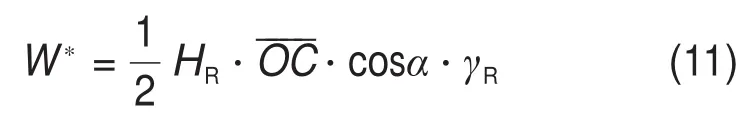
式中:α为滑动面倾角;γR为岩体重度。
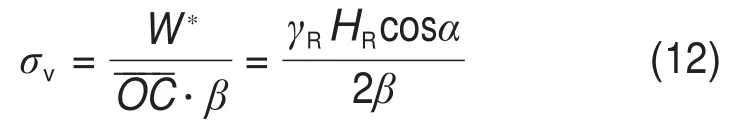
岩石自重部分的平均上覆压力hmR为

考虑土体自重:
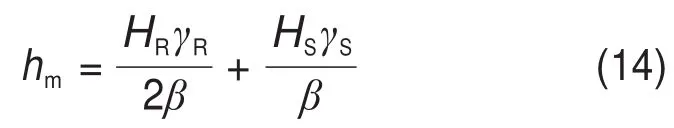
式中:γS为土体重度。
对于与边界1平行的应力分量t1及垂直的应力分量s1,有:
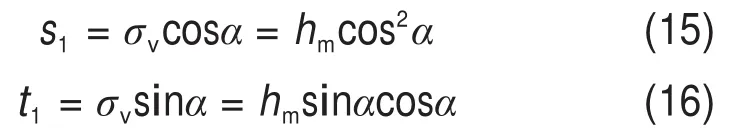
应力圆示意图如图3所示,其中,G圆代表大主应力圆,S圆代表小主应力圆,P为边界1上的点。由图3可知:可能存在2种类型的上覆压力,即被动压应力和主动压应力;当hm小于岩石无侧限抗压强度σcm时,边界1上的应力条件可能出现在应力圆上的任何位置;当hm大于σcm时,边界1的应力条件仅可能出现在应力圆的部分区域,其中,位于TL1和之间的应力因超过破坏标准故不存在,位于和0之间的潜在应力条件在实际中也不会出现。
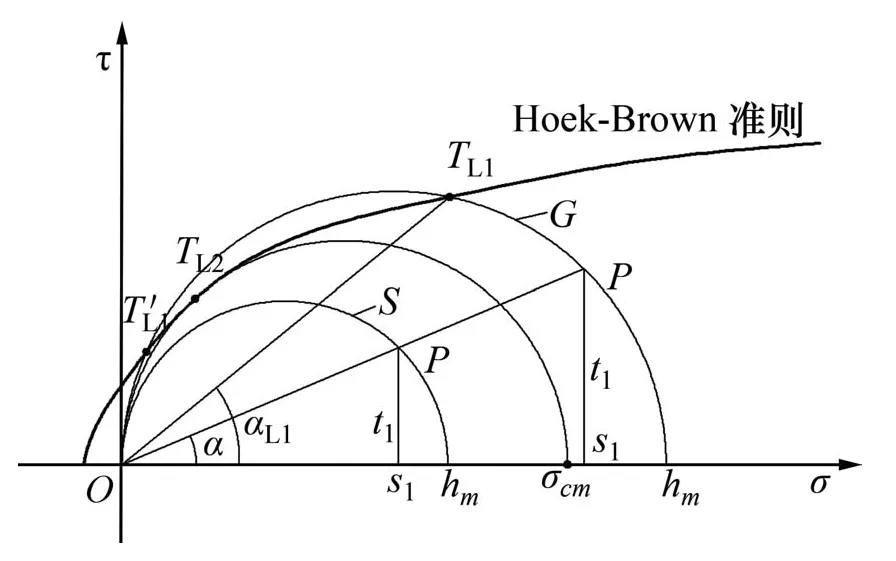
图3 应力圆示意图Fig.3 Schematic graph of stress circle
在实际中,小主应力圆的状态较为常见,最具有研究意义,故本文仅对的情况进行分析。
对于岩面倾斜的情况,倾角α可能为负(逆时针转角为正),应力条件仍可在应力坐标系中表示出来,相应的应力方向和强度准则的判定则随倾角α的正、负而直接改变,Hoek-Brown强度准则包线以应力坐标系横轴σ为对称轴进行翻转。
1.3.3 边界1应力圆分析
施加在假定滑动面OC的上覆压力σv和破坏面所承受的应力f与极限承载力σh相平衡(如图4所示),若这种平衡被打破,即发生破坏。
岩面倾角对于承载力的影响体现在滑动面倾角α,通过对α的分析可得到ρ1的求解方法。结合图3的几何关系,可得
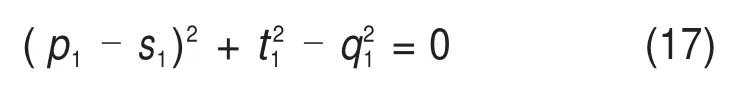
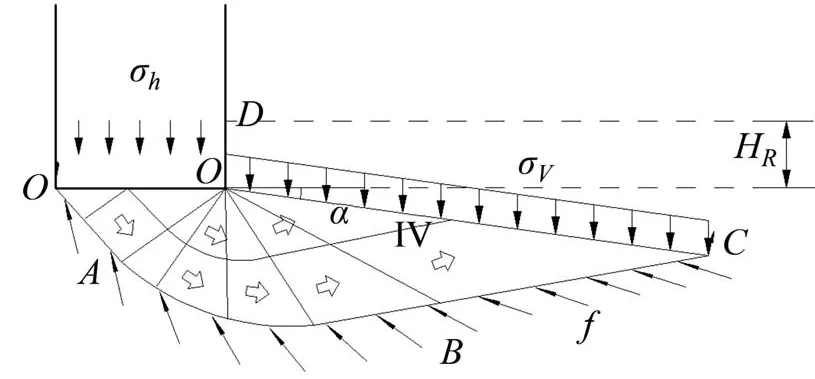
图4 破坏区域应力关系Fig.4 Stress relation of failure zone
式中:p1和q1为取决于瞬时摩擦角ρ的应力参数。
由式(17)可得,假定滑动面边界1的倾角α的表达式为
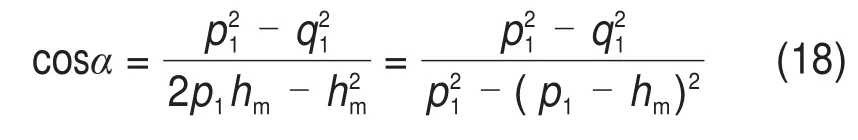
对于给定的hm,若α已知,则可确定ρ1,反之亦然。
当α>0时边界1的Mohr圆如图5所示。由图5可知:边界1相对于竖轴的大主应力倾角为
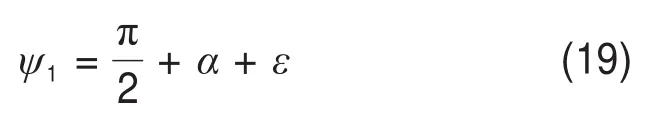
此关系式为边界1确定了大主应力σ1I的方向。从图5中的几何关系还可以推导出角度ε:

其中,边界1和边界2的大主应力σ1I与应力场的特征线方向形成的角度μ1和μ2分别为:
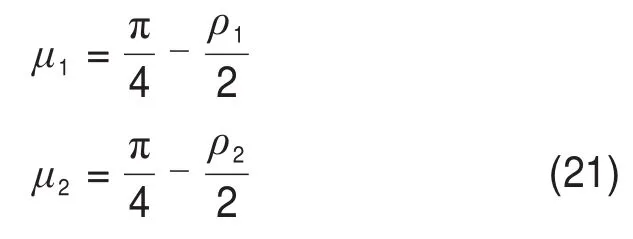
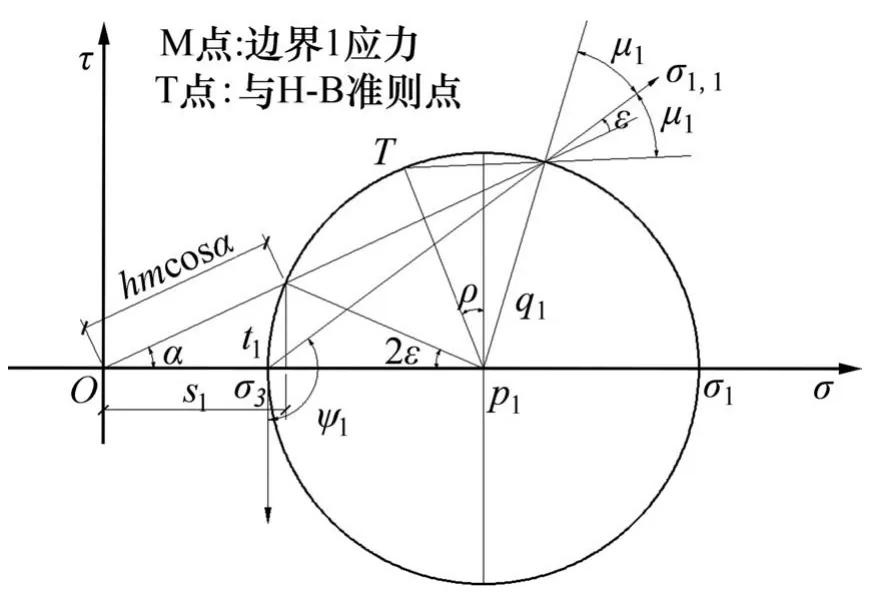
图5 α>0时边界1的Mohr圆Fig.5 Mohr circle of boundary 1 whenα>0
1.3.4 Riemann常量的传递与转化
根据滑移线的性质[16],沿一条滑移线上的Riemann积分常数相同,即可由已知边界的应力条件求得待求边界上的应力,并由此得出桩端的极限承载力。
对于边界1和边界2,有[10]:
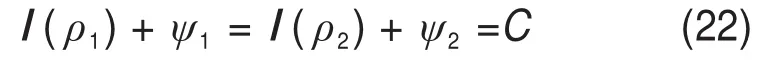
其中:C为固定常数;

鉴于实际情况下倾斜岩面桩荷载为垂直荷载,边界2主应力倾角为0°,即

1.3.5 嵌入比n
由图1所示几何关系,嵌入比n可表示为
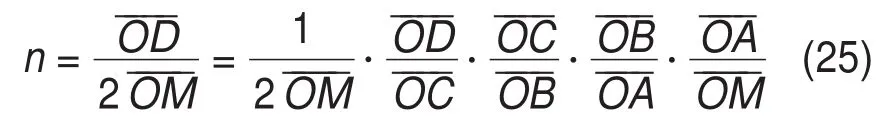
根据SERRANO等[15]的滑移线场结论,OABC区域有特定比例关系:
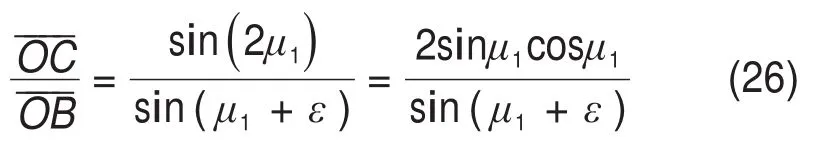
在塑性区中,下式成立:
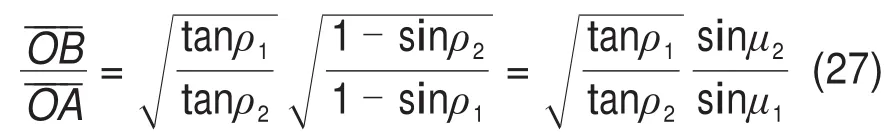
在桩底三角形O'OM的塑性区域,有

由三角函数关系可得DOC区域的关系,有
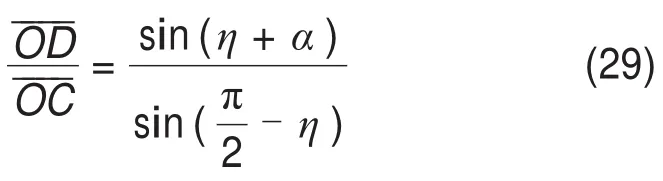
嵌入比n和其他量的关系式为

1.3.6 极限承载力
综上所述,在已知上覆荷载hm、嵌入比n、岩面倾角η和岩石强度参数ξ的情况下,通过联立式(8),(18),(20),(24)和(30),可得到6 个方程,求解6个未知量(α,q,p,ρ1,ρ2,ε),方程可解。
由于本非线性复杂方程组人工推导求解困难,故基于MATLAB软件编程求得数值解。
现已知边界1和边界2对应的瞬时内摩擦角ρ1和ρ2,可得到边界2的应力参数:

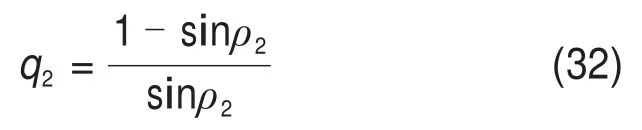
施加在边界2上的应力σ2为垂直应力,主应力如下:

桩底垂直应力即桩端极限承载力表达式为
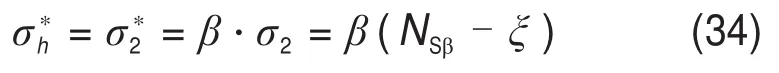
式中:NSβ为平面应变假设下的倾斜岩面嵌岩桩桩端荷载系数,
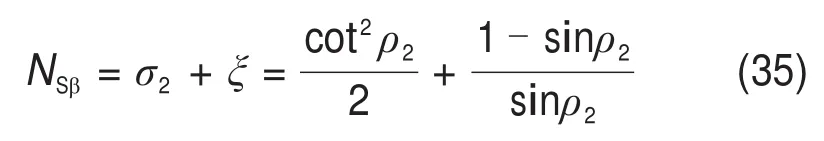
上述桩端承载力基于平面应变假设获得,但实际情况中必须考虑到桩的空间效应。为此,根据BEER[17]提出的关于桩的空间效应影响理论,引入倾斜岩面嵌岩桩形状系数sβ:

平均内摩擦角ρm与Hoek-Brown准则的斜率角度θ有以下关系:
因此,平均内摩擦角可由下式确定:
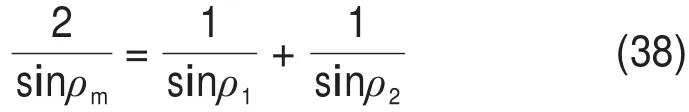
考虑空间效应后的荷载系数NSβP,有
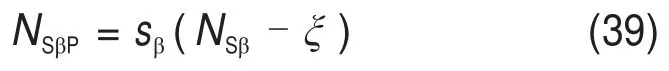
乘以系数β得到极限承载力:

2 算例
选取中等强度岩体材料[18]进行算例分析,参数如表1所示。
当岩面倾角0°时,模型转化为水平岩面嵌岩桩桩端承载力的计算,按照水平岩面嵌岩桩滑移线理论[10]进行计算,可得桩端竖向极限承载力为55.04 MPa,与采用本文提出的计算方法求解的桩端承载力结果一致。

表1 材料参数Table 1 Material parameters
3 参数研究
3.1 不同岩面倾角下嵌入比对承载力的影响
在上覆荷载hm=0.1和桩径为1 m的条件下,研究在不同岩面倾角下斜坡嵌岩桩的桩端承载力与嵌入比的关系,其中承载力以荷载系数NSβP体现。
图6所示为不同岩面倾角下桩嵌入比与荷载系数的关系曲线。从图6可知,随嵌入比增大,倾斜岩面嵌岩桩荷载系数NSβP呈增大趋势,桩端承载力逐渐增大;当嵌入比较小时,岩面倾角越大荷载系数越小;当嵌入比增大至一定值后,不同岩面倾角的倾斜岩面桩的承载力逐渐接近,达到某一定值时荷载系数不再增大,各岩面倾角状态下的桩端承载力一致,定义此状态嵌入比为极限嵌入比。
由图6还可知:当岩面倾角较小时,荷载系数增长率随嵌入比增大而减小;而当倾角较大时,增长速率呈先增大后减小趋势,说明岩面倾角越大,对桩端承载力的影响越显著;当达到极限嵌入比时,岩面倾角对桩端承载力无影响。
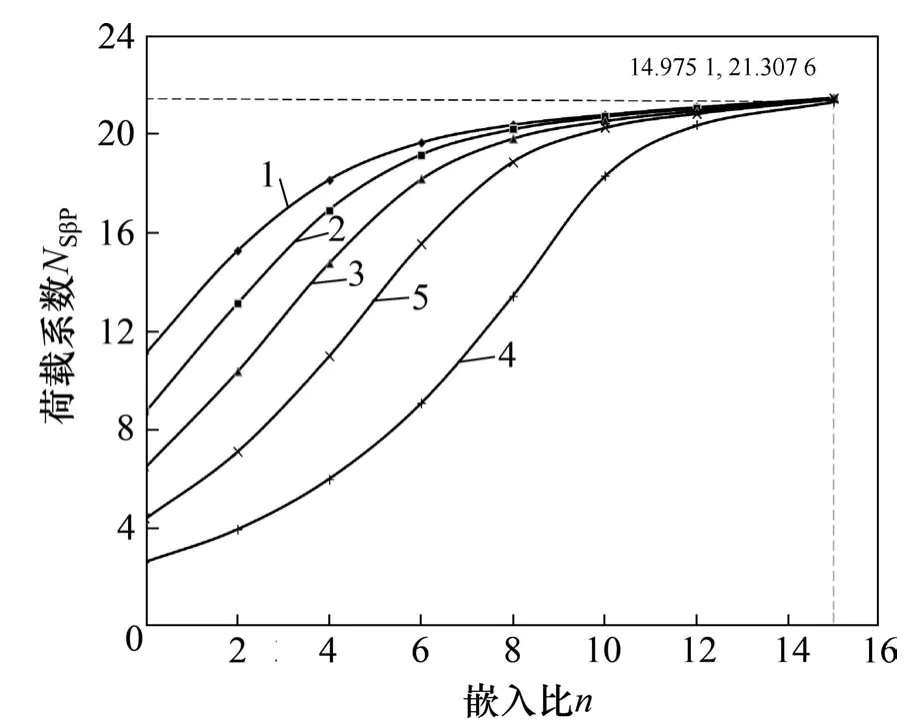
图6 ξ=0.005时嵌入比与荷载系数关系曲线Fig.6 Relationship between embedding ratio and load coefficient whenξ=0.005
3.2 不同岩面倾角下嵌入比对滑动面倾角的影响
在上覆荷载hm=0.1和桩径为1 m的条件下,研究不同岩面倾角下嵌入比与滑动面倾角的关系。图7所示为不同岩面倾角下桩嵌入比与滑动面倾角α的关系曲线。
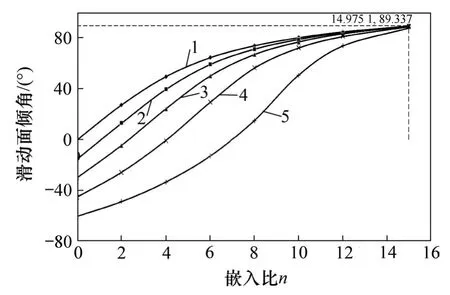
图7 ξ=0.005时嵌入比n与滑动面倾角关系曲线Fig.7 Relationship between embedding rationand dip angle of sliding surface whenξ=0.005
从图7可知,嵌入比n=0时所对应的α即为岩面倾角,随嵌入比增大,滑动面倾角α逐渐增大,或由负转正呈增大趋势;与图7所示关系类似;当嵌入比较小时,岩面倾角越大α越小,即可能为负值;当嵌入比增大至一定值后,不同岩面倾角情况的α逐渐接近90°,达到极限嵌入比时α趋近90°,并基本保持不变。
由图7还可知:当岩面倾角较小时,倾角α增长率随嵌入比增大而减小,而当倾角较大时,α的变化率呈先大后小趋势,这说明岩面倾角越大,对滑动面倾角的影响越显著;当达到极限嵌入比时,岩面倾角对滑动面倾角无影响,α均趋近90°。
3.3 岩石抗拉强度ξ的影响
由图8可知:ξ与极限嵌入比大致呈反比例关系,ξ愈大则该岩体的嵌岩桩极限嵌入比愈小。桩端岩体为小主应力破坏情况,即时,根据图8的曲线可确定不同岩石抗拉强度ξ所对应的极限嵌入比,该情况工程实际中也较为常见。例如,当岩体ξ=0.005时,仅在hm<0.2时可利用图8查得桩极限嵌入比。

图8 岩石抗拉强度ξ与极限嵌入比关系曲线Fig.8 Relationship between tensile strength ξ of rock and ultimate embedment ratio

图9 岩石抗拉强度ξ与最大荷载系数NSβP关系曲线Fig.9 Relationship between tensile strength ξ of rock and ultimate load coefficientNSβP
图9中ξ所对应的NSβP是在极限嵌入比状态下得到的,即为最大荷载系数,表示该岩体所能达到的最大桩端承载力。由图9可知:ξ愈大,则岩体的最大桩端承载力愈大,最大荷载系数的增长率减小,说明ξ对最大承载力的提升效果逐渐减弱。
4 结论
1)在不同岩面倾角下,嵌入比愈大,桩端承载力愈大,且岩面倾角越大,对于桩端承载力的影响越显著。当达极限嵌入比时,同种岩体的不同岩面倾角下的桩端承载力均达到最大。
2)在不同岩面倾角下,嵌入比愈大,滑动面倾角愈大,且岩面倾角越大,对于滑动面倾角的影响越显著。当达极限嵌入比时,同种岩体的不同岩面倾角下的滑动面倾角均趋近90°。
3)岩石抗拉强度与极限嵌入比大致呈反比例关系,提出在桩端岩体为小主应力破坏情况下的岩石抗拉强度-极限嵌入比关系曲线。岩石抗拉强度愈大,最大荷载系数愈大且增长率逐渐减小。
