利用历史信息和限制算子求解MOFJSP

吉训生，蔡益青

1.江南大学 物联网工程学院，江苏 无锡214122

2.物联网技术应用教育部工程研究中心，江苏 无锡214122

1 引言

当下，智能制造日益成为制造业发展的重要趋势和核心内容。从机器层面上来讲，智能制造要求机器具有柔性的生产制造能力，以实现“高效化”“绿色化”的生产目标[1]。柔性作业车间调度问题（Flexible Job-shop Scheduling Problem，FJSP）假设工序可在多台机器上加工，突破机器唯一性限制，是典型的柔性生产制造问题[2]。相比传统的作业车间调度问题（Job-shop Scheduling Problem，JSP），FJSP 是复杂度更高的NP-hard 难题，也是智能制造及组合优化领域的研究热点之一[3]。

为了实现绿色、高效生产，建设绿色工厂，必须要求合理调度柔性作业车间内的生产过程。通常，认为以满足消费者要求，降低生产成本、减小污染气体的排放等多个目标的FJSP是一个多目标柔性作业车间调度问题（Multi-Objective Flexible Job-shop Scheduling Problem，

MOFJSP）。MOFJSP需要优化多个性能指标（最小化最大完工时间、最小化生产、最小碳排放量等），而多个性能指标之间往往存在冲突。对于一个解来说，无法使所有性能指标都为最优值。因此，求解MOFJSP的目的是为了得到各性能指标的均衡解，称为Pareto 最优解[4]。多目标进化算法（Multi-Objective Evolutionary Algorithm，MOEA）因其在求解MOFJSP 时可获得一致性的Pareto最优解的特点，已成为求解此类问题常用的方法[5]。DEB 等[6]利用解之间Pareto 支配关系和拥挤距离，提出一种经典的MOEA——带精英策略的非支配排序遗传算法（Non-dominated Sorted Genetic Algorithm-II，NSGA-II）；张超勇等[7]将NSGA-II 作为求解MOFJSP 的策略，验证了NSGA-II在解决MOFJSP有良好的性能。Zhang等[8]提出一种基于问题分解的多目标进化算法（Multi-Objective Evolutionary Algorithm based on Decomposition，MOEA/D），此算法的求解速度都远高于NSGA-II；随后，Li等[9]将稳定配对思想引入MOEA/D，提出了基于稳定配对选择策略和分解相结合的多目标进化算法（Multi-Objective Evolutionary Algorithm based on Decomposition and Stable Matching，MOEA/D-STM），成功解决了MOEA/D“丢失解”的缺点；Wang 等[10]在多目标遗传算法（Multi-Objective Genetic Algorithm，MOGA）的基础上引入了免疫原则和熵，以保证种群的分布性，从而解决了早熟问题，提高收敛速度。

参考文献[10]的做法，本文在MOEA/D-STM 基础上提出一种基于历史信息和限制算子多目标进化算法（Multi-Objective Evolutionary Algorithm based on Decomposition with Historical information and Limited operators，MOEA/D-HL），并利用MOEA/D-HL 求解MOFJSP。此算法在保证收敛性的同时，提高了种群的多样性，增大进化强度，增强全局搜索能力，避免早熟。实验结果表明，本文算法在求解MOFJSP问题上比较可行且有效。

2 MOFJSP模型

MOFJSP 可用集合( M,J,O,T )来描述，其中M 代表机器，J 代表工件，O 代表工序，T 代表加工时间。通常设定有m 台机器( Mk,k ∈{1 ,2,…,m} )和n 个工件(J={ J1,J2,…,Jn} )，每个工件有多道工序，且工序的先后顺序是确定的，每道工序Oij(i=1,2,…,n,j=1,2,…,ni，ni表示工件i 所含的工序数）可由多台机器加工，所用时间tijk由机器能力唯一确定[11]。一个包括3 个工件、4 台机器的MOFJSP问题描述如表1所示。

表1 3×4 MOFJSP问题加工时间表

本文将最小化最大完工时间、最小化生产成本和最小化能耗作为优化目标，构建一个MOFJSP 模型[12-13]。求解MOFJSP 即在满足电力资源约束和工序先后约束的前提下，根据目标最优要求，把工序分配到各机器上并确定工序的加工序列和开始时间[14]，达到高效、绿色生产的目的。

MOFJSP优化目标如下：

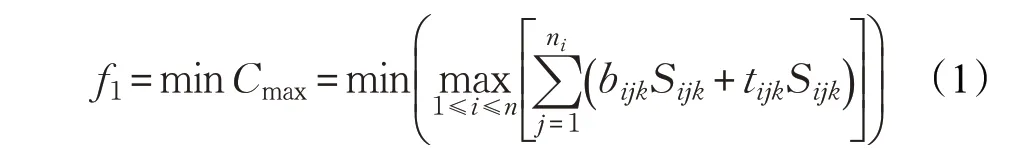
式中，bijk为工件i 的第j 道工序在机器k 上的开始加工时刻；tijk为工件i 的第j 道工序在机器k 上加工所用时间；Sijk为决策变量，若工序Oij在机器k 上加工则Sijk=1，否则，Sijk=0。

式中，γi为材料费；νijk为人工费，为工件的加工费用，表示使用第v 种供电方式在单位时间内为正常运行（额定负载）状态下的机器k 供电所需的成本，其中，v=1,2,3 分别表示使用主电网、分布式能源和燃机三种供电方式为机器提供能源；为机器空载运行费用，tk为机器k 在整个加工过程中的空载运行时间表示使用第v 种供电方式在单位时间内为空载状态下的机器k 供电所需的成本。

求解MOFJSP满足如下约束条件：

（1）在同一时段内，一台机器只能加工一个工件，即在某时刻h( )h ＞0 ，若1 则在i ≠p 或j ≠q 条件下，Spqk≠1 恒成立。

（2）同一个工件，只有在前工序完成后，才可加工下道工序，即：

其中，Cij表示工序Oij的完成时刻。

（3）任何一道工序一旦开始加工，就不可打断，即：

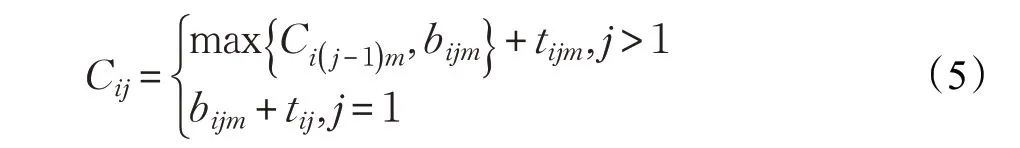
除了满足上述约束条件，还应做如下假设：

（1）某工件当前工序加工完成后，应立即运送至加工下一道工序所用机器前的缓冲器，若机器空闲应立即开始加工，否则在缓冲器中等待加工。

（2）工件在机器间的传送时间、在机器上的加工时间、装卸时间、调整时间统一视为加工时间。

（3）在加工开始前，所有机器处于正常待命运行状态，且所有工件同优先级。

3 求解MOFJSP的MOEA/D-HL

利用MOEA/D-STM 求解MOFJSP 时，在迭代过程中使用了无限制稳定配对选择策略，通过该策略选择的种群收敛性优于多样性，这将降低最终种群的性能[15]。另外，在交叉操作时只使用了父代信息，这会降低收敛速度。由于以上原因，本文选择有限制稳定配对策略作为选择策略，以平衡迭代过程中被选种群的收敛性与多样性；另外设置一个外部存储器用来存储每个个体的历史信息。历史信息表示个体上一次迭代时的状态。如图1所示分别表示第g+2 次进化操作时，x2、x4表示当前状态，则分别表示x2、x4的历史信息；同理，分别表示x2、x4在g+1 次进化操作时的历史信息。在交叉操作时，借助个体的历史信息以达到加速收敛的目的。利用MOEA/D-HL 求解MOFJSP的过程如图2所示。

图1 个体历史信息示意图

3.1 染色体编码与解码

图2 MOEA/D-HL算法流程图

编码是算法与MOFJSP 之间的桥梁[16]。本文选择基于工件工序和机器的双层整数编码，第一层为工序编码，第二层为机器编码。若有m 个待加工工件，每个工件有ni道工序，则染色体的每层编码长度为。具体步骤为：（1）在[0，1]之间，随机初始化长度为∑ni的实数数组；（2）根据每个位置上实数值的排名，确定其代表的工序；（3）通过工序编码的具体数值，确定所用的机器，并得到机器编码。

如图3所示，染色体表示3个待加工工件，每个工件有2～3 道工序，有3 台机器可用。随机初始化一组实数数组，通过比较每个基因位上的值确定排名，排名前3位的代表工件1 的三道工序，排名4、5 的基因位代表工件2 的两道工序，排名6、7 的基因位代表工件3 的两道工序，因此工序编码为[1 3 2 1 2 3 1]，表示工序[O11,O31,O21,O12,O22,O32,O13]。在确定工序编码后，从每道工序可用的加工库中，选择机器，并确定机器编码[2 1 3 2 2 2 1]，表示加工每道工序所用的机器分别为[M2,M1,M3,M2,M2,M2,M1]。

图3 染色体编码

解码的具体步骤为：首先根据工序编码确定工件及工序，然后从机器编码中找出对应的加工机器，并从时间矩阵中找到机器加工相应工序所需时间。通过上述操作，一条合法的染色体可通过解码操作得到一个可行、完整的调度方案。

3.2 进化操作

进化操作包括交叉和变异操作。交叉操作决定算法的全局搜索能力，是算法的关键[17]。如图1所述，本文交叉操作使用的种群历史信息存放在外部存储器中。算法开始时，初始化父代种群，同时将父代种群个体存放在外部存储器中，以初始化个体的历史信息。随后进行交叉操作，步骤如下：首先，从父代种群中选择三个染色体e1、e2、e3，并从外部存储器中选择染色体e1的历史信息h1；其次，选择从左向右依次在工序编码的基因位处随机产生r ∈(0,1]，若r ＜pc（pc为交叉概率），在父代染色体上选择此基因位为交叉点；最后，将两交叉点之间的基因进行交叉操作，并根据工序编码调整机器编码。如图4所示，选择a、b 为交叉点，对a、b 之间的基因位进行交叉操作：yr=e1+0.5×( e2-e3)+0.5( e1-h1)，生成子代染色体y 后，通过排序操作确定工序编码，并根据父代和子代信息确定机器编码。经上述交叉操作得到的子代染色体满足约束条件，是可行解。

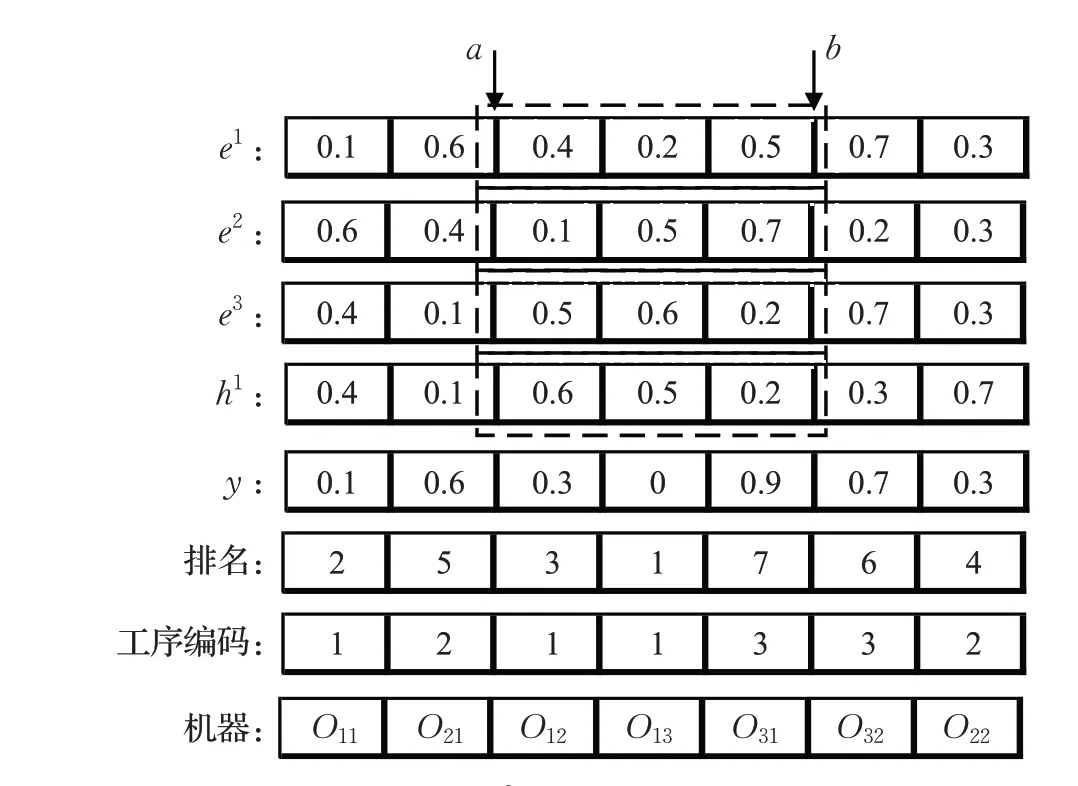
图4 交叉操作示意图

变异操作有利提高算法的局部优化能力和种群多样性，防止算法陷入局部收敛。本文选用变异操作过程如图5所示：在工序编码里随机选择基因a、基因b 进行交换，此交换将改变工序编码中每个基因所代表的工序，改变工序编码中每个基因所代表的工序，如c 位置的基因1 在原染色体表示工序O13，在新染色体变为表示O12，d 位置的基因3在原染色体表示工序O31，在新染色体变为表示O32，同时机器编码也随之变化。经此变异操作得到的新染色体能够满足约束条件。

图5 变异操作示意图

当一次进化操作结束后，将父代种群个体按顺序送入外部存储器，更新外部存储器所含历史信息，为下一次交叉操作提供历史信息。

3.3 选择操作

MOEA/D-STM 因其在构造偏好矩阵时，只用了解与子问题之间的欧氏距离和切比雪夫距离这两类信息，造成选择到的解多样性较差。如图6（a）所示，解拥挤在p1、p2之间，在下一次交叉和变异操作时，由于多样性的不足，使得生成的新染色体改变较小，一方面使收敛速度降低，另一方面容易使寻优过程陷入局部最优。为了提高父代种群的多样性，加速收敛，本文将解的位置信息引入到子问题对解的偏好矩阵的构造过程中，以增加那些离Pareto Front 远但分布均匀的解的被选择概率。主要操作有：（1）处理目标空间与生成待选解集；（2）获取解的位置信息，将位置信息代入自适应转移函数中，以得到限制信息；（3）构造带限制信息的子问题对解的偏好矩阵，以及解对子问题的偏好矩阵，并根据两偏好矩阵的信息选择父代种群。

（1）处理目标空间与生成待选解集

设目标空间为F(s)=[f1(s),f2(s),…,fd(s)]∈Rd,d 为目标空间的维数。使用一组均匀的权向量w={w1,w2,…,，将目标空间划分为N 个子空间，其中wt=(wt,1,…,wt,j,…,wt,d)∈Rd,wt,j≥0，且1，同时得到对应的子问题P={ p1,…,pl,…,pN}。将待选种群S={s1,…,sN,…,s2N}中的所有染色体通过目标函数值的计算，映射到目标空间中，得到待选解集X={x1,…,xN,…,x2N}，其中，x=[ f1( s),f2( s),…,fd( s )]∈Rd。

（2）获取限制信息

本文选用解相对于子问题的角度作为位置信息。将d 维目标空间F( s )=[ f1( s),f2( s),…,fd( s )]∈Rd转化为个二维空间，其中，表示从d 个变量中选出2个所有的组合方法。对于二维空间Fc( s )=[ fu( s),fv( s )],c=1,2,…,,u,v ∈[1 ,2,…,d ]，解x 在此空间中的目标值分别为fu( s),fv( s )，子问题ph对应的权向量wh在此二维空间的分量为wh,uv=( wh,u,wh,v)，则夹角分量为：arctan(| fu( s )-ωh,u|| fv( s )-ωh,v|),θuv∈[0 ,π/2]。角度θ 定义为：子问题ph与解x 在个二维平面上的夹角分量之和。

构造一个自适应转移函数，并引入位置信息θ，即：

（3）选择操作

将上述限制信息引入到子问题pr,r=1,2,…,N 对候选解x,x ∈X 的偏好值计算式中，如式（7）。利用式（7）可计算出子问题对所有候选解的偏好值，按升序排列则构成子问题对解的偏好矩阵ψp(N×2N)维 中的一行。

候选解x,x ∈X 对子问题pr,r=1,2,…,N 的偏好值计算式如式（8）。利用式（8）可计算出解对所有子问题的偏好值，按升序排列则构成解对子问题的偏好矩阵ψX( 2N×N维 )中的一行。

其中，‖ · ‖为欧氏距离，F( si)是将F( xi)归一化处理后的目标函数值，其第l 个目标函数值)/l=1,2,…,d ，其中，为最差点，可通过,l=1,2,…,d 计算。

利用两个偏好矩阵的信息和延迟接受程序[18]，得到最终配对结果如图6（c）所 示：} 。很明显，此种方法选择的解比不加限制信息的配对策略选择的解多样性更好。

4 实验设计与结果分析

NSGA-II 因其快速排序、快速估算拥挤距离以及容易比较拥挤距离的三个特点，成为CIMS 领域最常用的多目标算法之一。因此，本文将与NSGA-II 比较。NSGA-II和MOEA/D-STM需要设置的参数参照文献[19]。MOEA/D-HL 参数设置：种群染色体数目N=40，迭代次数K=400。为验证交叉概率pc，变异概率pm，限制算子控制参数L，邻域大小T 对生成调度方案的影响，本文进行了各相关参数的灵敏度分析。

4.1 灵敏度分析

采集某制桶公司实际生产车间的原始数据，取整处理后的数据如表2、3。车间设备名称与编号列于表2，6种桶，每种桶加工所需的20工序、可用的加工机械及所用加工时间列于表3。

以制桶车间实际订单为例，设置不同的实验参数，以三个目标值为参考，所得实验结果如表4所示。

从表5 可知，三种算法对pc、pm的值不敏感。另一方面，MOEA/D-HL中限制算子的控制参数对实验结果有较大的影响。因此，为了得到最佳实验结果，本文设置交叉概率pc=0.8，变异概率pm=0.6，限制算子控制参数L=1，邻域大小T=10。

4.2 实例仿真及结果分析

用3种算法求解该调度问题，不考虑工件在机器间转移的时间，实验参数不变。收敛性能见表5，MOEA/D-HL 所需最大完工时间、生产成本和C 排放量最优解分别为4 105 s、4 223.6元和39.5 g。从加工实时性上考虑，MOEA/D-HL性能优于NSGA-II、MOEA/D-STM，分别提高了0.8%，1.4%；在生产成本控制上，MOEA/D-HL较NSGA-II、MOEA/D-STM 提高了0.8%和1.8%；碳排放量是衡量绿色生产车间的一个重要指标，通过MOEA/D-HL 得到的调度方案对环境更加友好，较NSGA-II、MOEA/D-STM减少了2.5%和4.8%的碳排放量。另外，如图7 所示，MOEA/D-HL 收敛速度在整个进化过程中优于另外两种算法，也即MOEA/D-HL能更快地得到调度方案。

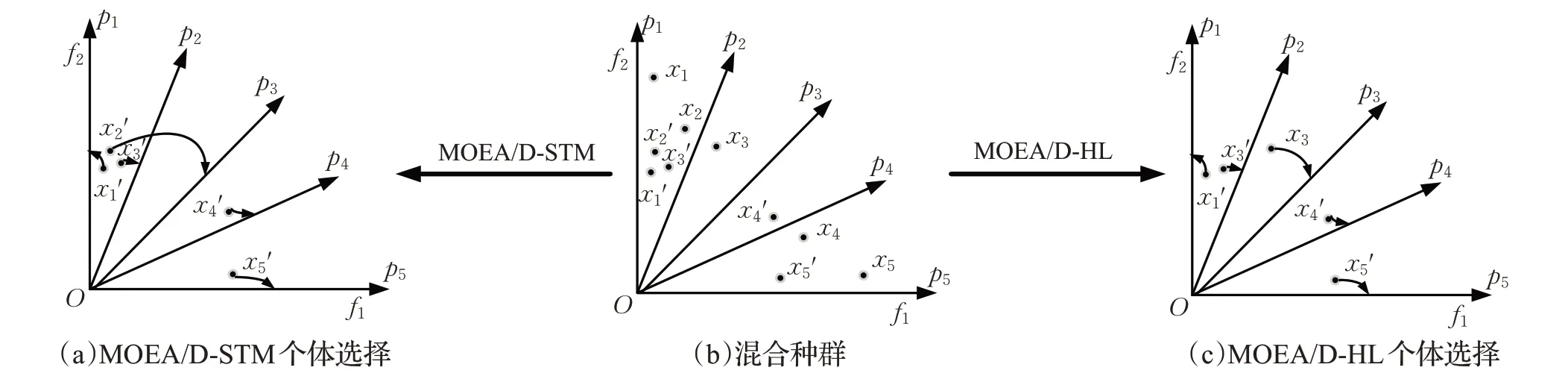
图6 MOEA/D-STM和MOEA/D-HL两者对比

表2 设备及编号

表3 工序与加工设备

表4 参数灵敏度分析

表5 实例仿真结果

图7 最大完工时间平均收敛曲线

5 结论

本文利用历史信息和带限制算子的选择策略，在保证良好收敛性的同时，加快了收敛速度。在生成子代的过程中，利用个体的历史信息，生成较大的进化量，在选择过程中，本文利用解在目标空间中的位置信息得到自适应限制信息，并将其加入到偏好矩阵的构造过程中，以获得分布性能好的父代种群，从而加快收敛速度。以某企业生产订单为例，验证MOEA/D-HL在解决实际生产车间调度问题时，收敛性和收敛速度优于MOEA/DSTM和NSGA-II，能够快速地获得收敛性能好的调度方案指导实际生产。