可容忍预测误差及其在汇率组合预测中的应用

陶志富，赵 勤，朱家明，刘金培

1.安徽大学 经济学院，合肥230601

2.安徽大学 数学科学学院，合肥230601

3.安徽大学 商学院，合肥230601

1 引言

1969年，Bates和Granger提出组合预测的概念[1]，通过统计的方法对单项预测的结果进行赋权并集成从而提高预测精度。自这一概念被提出以来，在理论上和应用上均成为近年来的研究热点[2-10]。

一般地，随着组合预测技术的广泛和深入开展，按照研究的内容不同，组合预测可以划分为信息的组合、方法的组合和结果的组合三种类型。其中，信息的组合以最有效和最直接的方式对预测的信息进行整合，例如某些行业数据综合指数的编制等；方法的组合则是将某些专业信息挖掘技术与预测技术相结合，以提高预测精度，例如智能算法与经典预测方法的结合等[7]；而结果的组合则是对若干单项预测的结果进行加权集成作为最终的预测结果[1，3-4]。本文遵循Bates 和Granger[1]给出的结果的预测这一组合预测概念，重点关注组合预测过程中单项预测结果权系数的确定。

传统的最优化组合预测模型以预测误差平方和达到最小、误差全距达到最小或误差绝对值达到最小为准则的目标函数，进一步确定各单项预测结果的权重系数。上述方法存在一定的缺陷，其原因在于，预测误差平方和、误差全距和误差绝对值易受极端值的影响，这导致在极端值点出现误差放大效应[11-14]，影响组合预测的预测精度。此外，在组合预测中，就同一种单项预测方法而言，在不同时点的预测精度可能不相同，即在某个时点预测精度较高，在另一时点预测精度较低[15]；而从多个单项预测结果看，在同一时点，不同单项预测方法给出的预测结果其精度也往往是参差不齐的。然而，在已有的组合预测理论探究中，鲜有文献对上述差异进行考量。

注意到在铸件加工过程中，为了保证加工质量，均规定了允许的误差范围，一方面其可以作为日常的生产标准，另一方面也可以作为铸件生产质量的保证。除此之外，在审计中提出了抽样结果可以达到审计目标所愿意接受总体最大误差的可容忍误差的概念[16]。可见，当给定一个可容忍的误差范围时，在实际的生产和管理实践中，均可以有效地控制考察对象的质量，提高实际运营过程的效果。

基于此，为了更进一步提高组合预测的预测精度，在上述概念和原理的基础上，本文提出一类预测可容忍误差的概念，并结合预测精度的相关概念，给出新的预测精度定义，并构建一个新的最优化组合预测赋权模型。另外，为从更多角度反映预测效果的好坏，本文除了运用普通的预测评价指标[15，17-20]对预测效果进行测度之外，还尝试运用统计学中均值、方差、峰度和偏度的概念[21-22]反映预测的效果。最后，以实例说明本文所构建的最优化组合预测模型的可行性与有效性。

2 基于可容忍误差的最优组合预测模型

预测误差反映了预测结果与实际观测序列值之间的离差，其数值的大小反映了预测结果的精确程度，两者之间呈反比关系，也即预测误差越小，表明预测效果越好，因而预测精度也就越高。考虑到同一时点不同单项预测结果精度上的差异，变权组合预测方法得以被提出并广泛应用到实践中[23-25]。为计算和控制抽样误差，抽样调查中考虑容许误差的范围及其确定[26]。审计问题中也有类似的可容忍误差的概念[15]。因而，对于预测方法，考虑引入可容忍误差的概念，从而能够反映预测结果在不同方法和不同时点上存在的差异及其效果。

2.1 可容忍误差以及相应预测精度的计算

设某社会经济现象的指标观察值序列为{yt,t=1,2,…,T},{t=1,2,…,T} 为某预测方法给出的预测值（或称拟合值）序列。

定义1 令：

为了应用上的方便，给出如下可容忍相对误差的概念。

定义2 令：

式（2）实质上也确定了预测值可容忍的区间范围，其依据实际观测值和δ 联合给出，也即

由定义1 和定义2 可知，可容忍误差只能观察某一时点的预测效果，为从整体上对预测结果的效果进行测度，在可容忍误差定义的基础上，给出如下精度的定义：

定义3 令，则对预测值序列，定义其可容忍精度为：

依据定义3，可容忍精度反映了预测值中位于可容忍误差内的预测值所占的比例。容易知道，其数值越大，表明预测的效果越好。

应用式（3），一个直接的反映预测可容忍绝对误差的测度可以计算如下：

2.2 基于可容忍误差组合预测模型建立

针对实际观测值序列{ yt,t=1,2,…,N }，设现有m种单项预测方法，其预测值序列分别记为,…,}2,…,N 。考虑到各单项预测结果之间存在的差异性，为充分利用这种差异性，设各单项预测方法的权重向量为ω=( ω1,ω2,…,ωm)T，组合预测结果可以表示为这里ωi≥0,i=1,2,…,m 且传统的组合预测考虑以组合预测误差平方和达到最小为准则，也即在上述权重应满足：

其中，eit=yt-yit,i=1,2,…,m；t=1,2,…,T 表示第i 种单项预测方法在第t 时刻的预测误差。

为消除可能存在的极端值的影响，在上述可容忍误差概念的基础上，考虑新的组合预测赋权模型。

注意到，可容忍绝对误差ε 值的水平越大，预测的可容忍精度也越大，但是预测值可能偏离实际值的程度也越大。换言之，可容忍预测精度与ε 值正相关但是实质上总是希望ε 的值尽可能小而可容忍精度的值尽可能大，这是两个矛盾的目标。

为此，构造如下的多目标规划问题：

其中，πi,i=1,2,…,m 为第i 种单项预测方法的可容忍预测精度，y^it为第i 种单项预测方法在第t 时刻的预测值。

模型（5）的第一个约束表明在考虑可容忍误差的条件下，组合预测的可容忍精度应大于单项预测中的最大者，其可以通过MATLAB或者Lingo软件进行求解。

综上，基于可容忍绝对误差的组合预测赋权模型是普通最优化模型的推广，其组合预测步骤如下：

步骤1 由式（5）计算各单项预测方法的权重向量

步骤2 依据公式对各单项预测结果进行集成，得到组合预测预测值序列t=1,2,…,T 。

步骤3 对组合预测的结果进行效果评价和对比分析。

步骤4 就样本外时点进行预测。

这里，在对预测结果的效果评价时，除了常规的几个误差指标外，本文还考虑对不同预测结果的残差从均值、方差、偏度和峰度等基本的描述性统计指标进行对比和分析。应用这些指标对不同预测结果的残差进行效果分析的优点在于可以从宏观上对预测结果的状态进行掌握，进而提高分析的全面性。

3 实证分析

为了验证本文所构建的最优化模型的有效性，本文运用2016 年1 月4 日至2018 年6 月12 日的日元兑美元日汇率收盘价的数据进行了实证研究，并将样本分为两个部分，其中将2016 年1 月4 日至2018 年5 月31 日的625 个数据作为训练样本，用于建模；2018 年5 月31 日至2018 年6 月12 日的10 个数据作为检验样本，并用于验证模型的有效性。

针对625个样本，构建如下的单项预测方法：

（1）BP神经网络（BPNN）预测

BP神经网络模型的一类典型互联模式为一个多层感知器结构，即包含输入层、输出层和若干隐含层（有时可加该层）并组成前向连接模型，其中同一层级神经元互不连接而相邻层级之间的神经元通过权值连接。图1给出一类典型的三层BP神经网络结构模型。

图1 典型的三层神经网络结构模型

通过模拟生物神经元的非线性特性，BP 神经网络选用如下的S型输出函数：

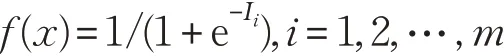
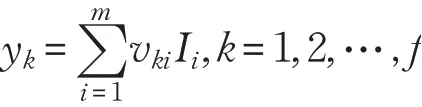
这里，vki为输出层神经元k 与隐含层神经元i 的连接权值。

神经网络模型的基本原理是将观测值序列作为输入，而将预测值作为输出，利用自购的样本训练这个网路，使得不同的输入向量得到不同的输出值。这样，神经网络所具有的连接权值便是经自适应学习所得到的内部表示，因而训练好的网络便可作为定性和定量相结合的有效工具对不同的预测对象进行预测[27]。

本文选取前70%的数据作为训练样本，中间15%数据作为测试数据，最后15%作为验证数据。

运用MATLAB运行结果如图2所示。

（2）非线性自回归神经网络（NARnet）

图2 BP神经网络预测效果图

非线性自回归神经网络[28]是一类记忆功能的网络，其结构包含输入层、隐含层和输出层以及输入和输出的延时，网络的输出取决于当前的输出和过去的输出，其方程为：

其中，y(t)表示输出，d 为延时阶数，f 表示应用神经网络实现的非线性函数。

本文选取80%为训练样本，10%为检验样本和10%测试样本。运用MATLAB 分析，应用MATLAB 得到的拟合结果如图3所示。

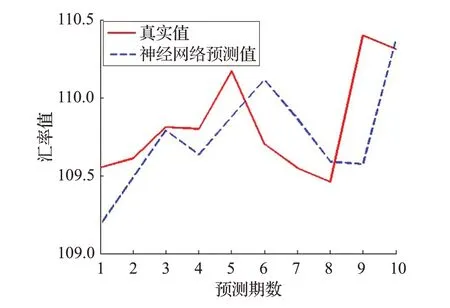
图3 NARnet预测效果图

（3）自适应神经模糊推理预测方法

自适应神经模糊推理（Adaptive Neuro-Fuzzy Inference System，ANFIS）能够直接通过模糊推理实现输入层与输出层之间的非线性映射，与神经网络的信息存储能力和学习相近[29]。

典型的ANFIS模型结构具有5层，即计算输入的模糊隶属度、每条规则的适用度、适用度的归一化、每条规则的输出和模糊系统的输出。

图4给出具有两个输入单个输出的ANFIS结构[30-31]。

图4 具有两输入一输出一阶ANFIS结构

模糊推理的输出采用如下形式的加权平均法：

这里，wi为变量xi的权重。

类似地，选取前70%观测值为训练数据，中间15%为测试数据，最后15%为验证数据。通过MATLAB 分析可以得到如图5。

图5 ANFIS预测效果图

通过训练样本的625个数据建立模型，预测样本外的10个数据，最终的单项预测结果如表1所示。

首先，通过本文所构造的多目标最优化模型（5），利用Lingo软件运行得到一组权重（全局最优解）如下：

结果表明，由于各单项预测结果精度均相对较高，因而在进行组合时经过对误差的可容忍限制，最优化模型给出了较为一致的权重分配。这也从另一个侧面反映出普通等权重赋权结构在实际应用中的合理性[32]。通过对各单项预测结果集成，计算出组合预测值，如表1所示。

作为对比，考虑传统的以组合预测误差平方和达到最小为准则构造权重的方法，利用Lingo软件运行得到如下的一组权重：ω1=0,ω2=0.053,ω3=0.947。

表1 实际值及预测值

为了验证基于可容忍误差的最优组合预测方法权重构造的有效性，本文从如下两个方面对所提出的模型的有效性进行验证：

（1）对本文的单项预测结果及组合预测结果的残差进行描述性统计分析，分析结果如表2所示。

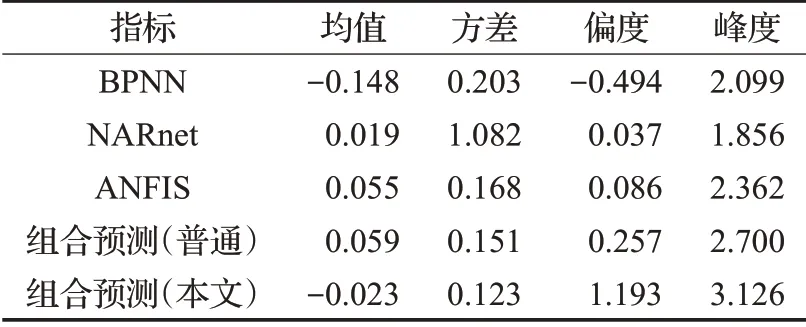
表2 模型的偏度及峰度

均值是反映数据的平均水平，表2的数据反映的是残差的均值，残差的均值的绝对值越接近于0，表明预测结果越好，仅仅从均值的角度可以得出，NARnet模型的预测效果比较好。

从方差的角度分析，方差是反映数据的离散程度，方差越接近0，表明数据的离散程度越小，从表2中可以看到，本文所提出的组合预测模型的预测效果比较好。综合残差的均值和方差两方面看，组合预测的预测效果要优于各单项预测方法；本文所提出的组合预测方法优于普通的组合预测方法。

偏度是反映数据分布对称性的测度，偏态系数为0，则说明该组数据的分布是对称的。本文考虑的是残差的偏度，从表2中可以看到，NARnet模型的偏度更接近于0，表明此模型的残差序列分布近似于对称分布，预测效果更好。

从峰度的角度考虑，不论是组合预测模型还是单项预测模型，其峰度都是大于0 的，表明各个模型的残差分布是比较集中的，其中本文所提出的组合预测方法的峰度更接近于3，更趋向于正态分布，其残差分布更集中；其次是普通的组合预测方法的峰度更接近于3。因此，可以得出，组合预测方法优于各单项预测方法，本文所提出的基于可容忍度的组合预测模型优于普通的组合预测模型。

此外，可以绘制各单项预测方法及组合预测方法的残差绝对值图，如图6所示。

图6 预测结果和效果对比

由图6（a）可见，单项预测结果的预测效果较差，两种组合预测的结果都优于单项预测方法，并且随着时点的推移，本文所提出的组合预测方法与实际值越接近。

由图6（b）可见，单项预测方法在各时点的残差波动比较大，基于可容忍误差的最优化组合预测模型的残差波动相对较稳定；另外，本文所提出的组合预测模型的残差略小于传统的组合预测模型。

为了更好地对预测结果进行分析，不能仅仅局限于对预测结果的残差序列进行描述性统计分析，于是，本文从如下几个普通的评价指标考虑，对其预测结果的好坏进行分析。

（2）运用常用的几种误差评价指标对单项预测结果及组合预测结果进行分析，结果如表3所示。

由表3，本文可以得出以下结论：

（1）相对于三种单项预测方法而言，从四种评价指标来看，不论是相对指标还是绝对指标，组合预测模型的预测结果均优于单项预测方法。

表3 模型拟合效果比较

（2）相对于以预测误差平方和达到最小为准则的普通加权组合预测方法，本文所提出的方法由于考虑到了可容忍误差，提高了组合预测的精度。

（3）由于单项预测方法均采用了精度较高的智能预测方法，在组合结果改善了预测效果的同时，结果改善的幅度相对偏小。但是，仍可以观测出通过简单的附加可容忍误差的条件，预测效果整体而言仍是占优的，表明了所提概念和方法的有效性。

4 结语

本文基于可容忍误差的概念，并结合预测精度的相关概念，给出新的预测精度的定义，并构建了一个新的最优化组合预测赋权模型。另外，为从多角度反映预测精度的好坏，本文除了运用普通的预测评价指标对预测效果进行测度之外，还尝试运用统计学中均值、方差、峰度和偏度的概念反映预测的效果。并以实例说明本文所构建的多目标最优化组合预测模型的可行性和有效性。

可容忍预测误差作为传统预测误差的推广，本文仅将其应用到组合预测赋权问题中。未来，这一误差测度可以进一步推广到各单项预测方法中，例如，通过设定可容忍绝对误差水平，考虑多元线性回归模型中的参数确定。同时，也可以将可容忍预测误差拓展到基于误差的预测方法构建和评估问题中。