基于可协调经验小波变换的多聚焦图像融合

宫 睿，王小春

北京林业大学 理学院，北京100083

1 引言

由于光学透镜的局限性，大部分相机的景深是有限的，使得只有在景深范围之内的物体是聚焦的，可以清晰成像，而景深范围之外的场景是散焦的，其成像会存在或多或少的视觉模糊。由此可知，通过拍摄直接得到一幅全聚焦图像是十分困难的。然而，为了准确分析和理解，人们往往希望获得场景中所有目标对象都清晰的图像，多聚焦图像融合是实现此目标的有效方法之一。多聚焦图像融合就是从多个部分聚焦图像中提取聚焦区域，并按一定的融合算法生成所有对象都聚焦的合成图像的过程。多聚焦图像融合是图像融合的一个重要分支[1-2]。

小波变换[3]因其良好的时频局部性和多分辨性，已成为非平稳信号分析的常用工具，被广泛应用于包括图像融合[4-5]在内的图像处理之中。基于小波变换的多聚焦图像融合算法主要由三步组成：首先，在选定小波基和确定分解层数N 的前提下，对待融合的两幅图像分别进行小波变换；然后，采用合适的融合规则对高低频小波系数分别进行融合，得到融合小波系数；最后，基于融合小波系数，用小波逆变换进行重构，得到最终融合图像。但是传统的小波变换依赖于规定的尺度细分方案和固定的小波函数和尺度函数，不是完全自适应的信号分析工具。在小波对图像的分解过程中，滤波器组是事先选定的，与图像的特性无关。显然，固定不变的滤波器组不可能对任何图像都达到最优表示。

Huang 等人[6]1998 年提出的经验模态分解（EMD）算法是一种自适应的信号分析方法，其核心思想是在一定的迭代和筛选过程中，检测出代表信号的主要“模式”。由于EMD能适应性地分离出信号的高低频分量，近十多年来受到了学者们的广泛关注，成为非线性和非平稳信号分析的有效工具。然而，EMD 算法仍然存在一些明显的缺陷，其一，分解结果中容易出现虚假模态和产生混频现象；其二，EMD 是一种算法式的方法，缺乏严格的数学理论基础，且难以用数学模型进行描述，导致人们很难真正理解EMD分解提供的内容。

为了改进EMD方法，Gilles结合小波分析的理论框架和时频平面重新划分的思想，于2013 年提出了一种称为经验小波变换（Empirical Wavelet Transform，EWT）的自适应信号分析工具[7]。该方法首先根据信号的傅里叶谱的支撑，对傅里叶谱进行自适应划分；然后根据Meyer小波的构造方式，在频域定义经验尺度函数和经验小波函数；最后利用相应的滤波器对信号进行滤波，实现不同调幅-调频成分AM-FM的提取。EWT与传统小波变换有着本质的不同，传统小波变换的分解频段是固定的，引入的尺度因子与信号的频率没有直接联系。而EWT 对时频平面的划分是自适应的，其中的尺度因子是根据研究信号的信息经验检测而得到的。利用EWT 可以实现信号在任意频段的分析。至今，EWT 已被用于机械故障诊断[8]、信号去噪[9]等方面。EWT 作为一种新型的信号处理方法，其作用和意义仍在不断探索之中。

针对多聚焦图像融合问题，本文首次将经验小波变换引入其中，为了保证多幅源图像具有相同的分解层数，以及对应子带具有相匹配的特性，以满足图像融合对图像多尺度分解的要求，本文在EWT的基础上，提出了一种自适应可协调经验小波变换，并根据多聚焦图像在该变换下的低高频子带特性构造合适的融合规则，实现多聚焦图像融合。

2 经验小波变换

EWT 是一种具有严格理论支撑，且包含经验信息的自适应小波分析工具。它不依赖于预先指定的基函数，而是根据信号本身的特性自适应地生成一组在频域内具有紧支撑的正交小波基函数。

经验小波变换的主要思想是：首先根据信号的傅里叶谱的特性，进行频谱分割；然后在被分割的频谱上生成带通滤波器，形成滤波器组。最后使用滤波器组对信号进行滤波，得到表征信号内在模式的各成分分量。一维经验小波变换的算法[7]（简称为算法A）步骤具体如下：

（1）获取信号的时域离散表示f(n)，其中，n 为自变量，其取值为正整数；设置谱带数量N ，即模态分量个数。

（2）将频率范围归一化至区间[0,π]，对信号f(n)进行快速傅里叶变换（FFT），得到信号频谱F(ω)，其中ω为频率，取值区间为[0,π]。

（3）寻找信号频谱F(ω)的N 个局部极大值点，确定N 个区分模态分量的显著值，并将其从大到小排列。

（4）计算相邻两个局部极大值点之间的中间频率点ωm(m=1,2,…,N-1)，并将其作为频谱分界点。

（5）用N+1 个边界点ωm（其中ω0=0,ωN=π）将[0,π]划分成N 个区间Λn=[ωn-1,ωn]，根据Meyer 小波的构造方式，定义经验尺度函数和经验小波函数，得到滤波器组

（6）对信号f(n)使用滤波器组中的滤波器进行滤波，得到信号的N+1 个时域表示。

步骤（5）中的经验尺度函数和经验小波函数分别由以下公式（1）和（2）构造，其中参数γ 的取值范围和函数β(x)分别由公式（3）和（4）给出：

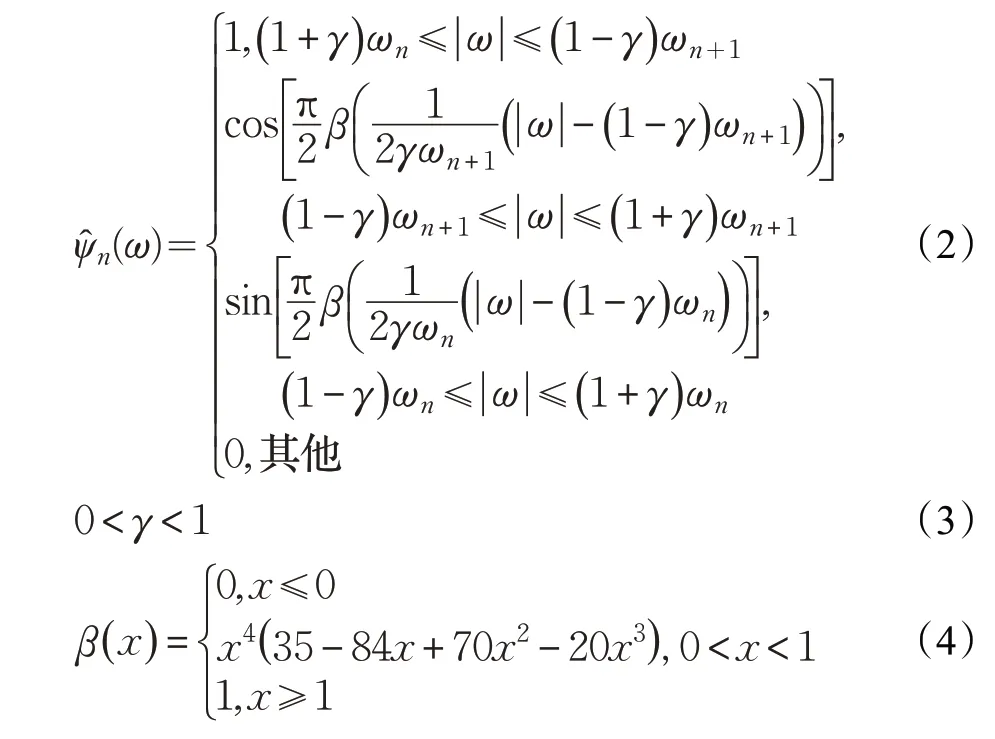
一维经验小波变换可以依据张量积的方式扩展应用到二维图像信号上，具体步骤如下：

（2）对图像f 的每一列进行FFT，得到频谱f(ω,j )，其中，Ncol为图像的列数，j 为列标。并求得所有列的傅里叶频谱均值

（5）使用行滤波器组中的滤波器对图像按行进行滤波，得到NR+1 个中间结果。

（6）使用列滤波器组中的滤波器对NR+1 个中间结果分别按列进行滤波，得到最终( NR+1) ×( NC+1)个子带图像。

3 基于C-EWT的图像融合算法

3.1 可协调经验小波变换

EWT 所用滤波组是根据信号自适应生成的，一般来说，不同图像的EWT 分解结果具有不同的子带图像个数。即使子带图像个数相同，其频谱区间的划分也未必完全一致。然而，图像融合需要对匹配的子带图像逐一进行处理，若直接利用EWT进行分解，会因不同频率模式的混合导致融合结果中出现频谱混叠或频带缺失的现象。

为了解决上述问题，本文提出了一种适合于图像融合算法的可协调经验小波变换（Coordinative EWT，CEWT）。C-EWT 同时利用两个及以上源图像生成滤波器，以保证待融合图像具有相同的谱带数量和频谱划分区间。下面以两幅待融合图像为例给出C-EWT算法的具体步骤如下：

（1）对两幅图像的每一行i 进行快速傅里叶变换，得到频谱，计算两幅图像所有行傅里叶频谱的均值，其中Nrow为单幅图像的行数。

（2）对Frow执行一维经验小波生成算法，即算法A 中的步骤（3）～（5），得到一个行滤波器组,，其中NR是行滤波器组中经验小波函数的个数。

（3）对两幅图像的各列执行上面（1）、（2）步骤中类似的操作，得到所有列傅里叶频谱的均值，并由此得到一个列滤波器组，其中Ncol为单幅图像的列数，NC是列滤波器组中经验小波函数的个数。

图1 不同聚焦的“Clock”图像及其C-EWT分解结果

为了验证C-EWT 分解的有效性，对将要参加融合实验的两幅多聚焦图像（如图1（a）、（b）所示）进行了CEWT 分解。图1（c）和（d）分别表示图1（a）和（b）的CEWT分解结果，其中，各图像的行、列谱带数均设置为3。为了方便查看，图1（c）和（d）中的每一子图的尺寸均被缩小，其真实尺寸与源图像1（a）、（b）一致。比较图1（c）和（d）可以发现，最下面一行右边的两个对应子图差别较大，很明显，聚焦部分的细节更加丰富，说明C-EWT能很好地识别图像的聚焦部分。其他对应子图像差别很小，体现了两幅源图像整体轮廓信息的相似性。实验结果表明C-EWT能很好地描述多聚焦图像的特性。

3.2 本文融合算法

基于C-EWT 分解方法，本文提出了一种新的图像融合算法——基于C-EWT 的多聚焦图像融合算法，该算法的框架如图2 所示。算法涉及的待融合图像均已完全配准。具体步骤如下：

步骤1 对两幅源图像A,B 分别进行C-EWT分解，得到低频子带图像AL,BL,和多个高频子带图像AHi,BHi，即：

其中，n 为高频子带个数。

步骤2 使用高频融合规则分别对第i(i=1,2,…,n)个高频子带AHi和BHi进行融合，使用低频融合规则对低频子带AL和BL进行融合。

步骤3 对步骤2 得到的各分量的融合结果进行CEWT逆变换，即可得到最终的融合图像。

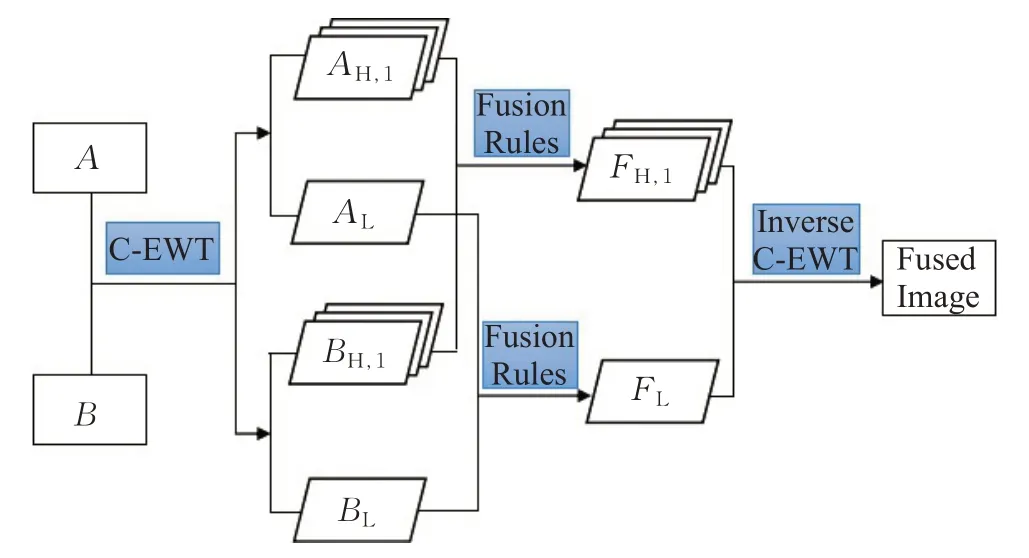
图2 基于C-EWT的图像融合框架

3.3 融合规则

在图像融合算法中，融合规则的选取也是另一个至关重要的步骤。一般情况下，图像多尺度分解下的高频分量和低频分量具有不同的图像特征。根据C-EWT分解的特点，本文对C-EWT 分解下的低频分量和高频分量分别设计融合规则。

3.3.1 低频分量融合规则

C-EWT 的低频分量，反映了源图像的概貌特征及总体灰度值分布情况。为了能够较好地保存源图像的概貌特征和总体灰度信息，本文对低频分量AL,BL采用基于改进Laplacian 能量和（SML）[10]的阈值匹配选择与加权的融合规则。

图像f 中任意一点(x,y)处的改进Laplacian 能量和定义为：

其中，M×N 代表局部邻域窗口的大小，M 和N 一般为奇数（本文取M=N=3）；MLf(x,y)代表图像f 在点(x,y)处的改进Laplacian能量，定义为：

低频分量的融合规则计算如下：

（1）根据式（5），分别计算AL和BL在中心像素(x,y)处的SML：

（2）由式（7）、（8）定义AL和BL在中心像素(x,y)处的SML匹配度(x,y)，计算如下：

其中：

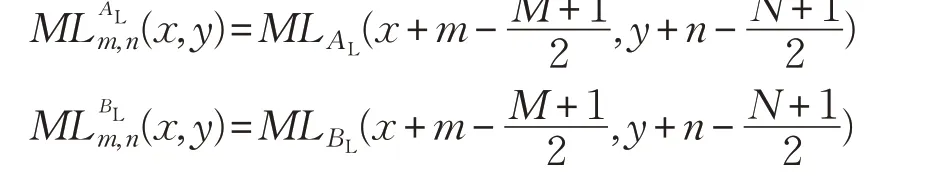
（3）确定融合图像F 的低频分量FL。定义一个匹配度阈值T1（一般取值范围为0.5～1，本文取0.7），如果＜T1，则选用SML 最大的系数作为融合系数，即：

否则，执行加权规则：

3.3.2 高频分量融合规则

C-EWT 的高频分量包含了源图像的细节信息，如边缘、纹理、线条等，因此合理选择高频融合规则对保持源图像的细节特征极其重要。目前多数高频分量融合都采用绝对值取大的融合规则，此方法的不足之处在于没有考虑像素之间的相关性，容易导致细节信息损失和图像扭曲。为了改进融合效果，本文采用局部Log-Gabor能量取大的融合规则对高频分量进行融合，这种方法符合人眼视觉对像素局部区域内的整体突变特征较为敏感的特性[11]。

Gabor滤波器[12]是借鉴生理学研究中方向可选神经元的计算机制提出的一种有效的纹理特征提取算子。它以Gabor 函数作为小波基，既具有尺度不变性，又能有效地提取图像特征。Log-Gabor 滤波器[13]是在Gabor滤波器的基础上提出的，该滤波器的尺度可以随意变化，弥补了Gabor 滤波器对高频分量表达不足的缺陷，同时能够大幅减少信息冗余。

图像f 中任一点(x,y)处的局部Log-Gabor 能量[14]定义为：

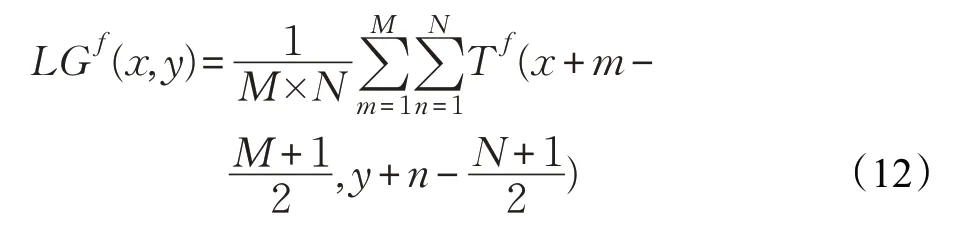
其中，M×N 代表局部邻域窗口的大小，M 和N 一般为奇数（本文取M=N=3）；Tf(x,y)表示图像f 在(x,y)处的Log-Gabor能量值。

由于Log-Gabor 能量能够反映图像的局部纹理特征，而多聚焦图像的高频分量在聚焦区域拥有比散焦区域更多的细节信息，因此，对高频分量采用表示纹理特征的Log-Gabor 能量取大融合规则能有效地提取图像的聚焦区域。

高频分量AHi和BHi(i=1,2,…,n)的融合规则按照以下步骤实现：

（1）根据式（12），分别计算AHi和BHi在像素(x,y)处的Log-Gabor能量：

（2）确定融合图像F 的高频分量FHi。采用Log-Gabor能量最大的系数作为融合系数，即：

4 融合结果及分析

4.1 实验设置

为了验证本文算法的有效性，设计了大量的比较实验，将其与基于小波变换的方法（DWT）、基于Contourlet变换的方法（CT）、文献[15]中的基于人眼感知特性的NSCT域方法（简记为文献[15]）、文献[16]中的基于自相似性和深度信息的空域方法（简记为文献[16]）、文献[17]中的基于PCNN的NSCT域方法（简记为文献[17]）以及文献[18]中的基于多尺度变换和稀疏表示的方法（简记为文献[18]）等进行比较。其中，DWT 的基函数为Haar小波，分解层数为3层；CT的分解层数及各层方向数为[1，4，8，16]，LP 和DFB 均采用pkva 滤波器；DWT 算法和CT 算法中采用经典的低频加权平均、高频取大的融合规则；其余四种对比算法的参数设置与融合规则均与原文献一致。

选用4组已配准的多聚焦图像进行仿真对比实验，如图3 所示。其中，前三组为常用标准测试图像，最后一组（wheel）为通过人工在不同区域内进行Gaussian局部区域模糊得到的图像。图3（a）中右侧大钟表为聚焦区域，左侧小钟表处于离焦状态，而图3（b）正好相反，聚焦区域为左侧小钟表。图3（c）中，远处部分为聚焦区域，包括人、电脑等，而图3（d）的聚焦区域则为近处的钟表，其余部分都较模糊。图3（e）～（h）中各自的聚焦区域已在图中说明。

图3 四组待融合多聚焦图像

实验所用计算机为：64位Win7操作系统，内存8 GB，Intel®CoreTMi5-4590 CPU @3.30 GHz。所用编程环境为Matlab R2016a。

4.2 实验结果分析

图4 不同方法对多聚焦“clock”（图3（a）（b））的融合结果（Group1）

图5 不同方法对多聚焦“lab”（图3（c）（d））的融合结果（Group2）

图6 不同方法对多聚焦“pepsi”（图3（e）（f））的融合结果（Group3）

图7 不同方法对多聚焦“wheel”（图3（g）（h））的融合结果（Group4）

图4～7分别给出了图3中四组多聚焦图像的融合结果。为了方便，记图4、图5、图6、图7所示融合结果分别为Group1、Group2、Group3、Group4。可以看出，七种方法均能有效利用待融合图像之间的互补信息，融合图像一定程度上包含了各聚焦区域的细节信息。但各方法的融合结果具有一定的视觉差异。相比于其他六种方法，本文算法有更好的视觉效果。对比图4（a）～（h）可以看出，基于DWT、CT及文献[18]的方法所得融合结果中有虚影模糊现象（如左侧钟表的边缘处）；文献[15]方法的结果在左上角有条纹状噪声；而本文算法所得融合结果既无条纹状噪声也无虚影模糊现象。对比图5（a）～（h）同样可以看出，基于DWT、CT及文献[15]的方法所得融合结果中也存在虚影现象（如人物头部周围），文献[17]方法的结果中人物头部存在白色噪声，文献[18]方法的结果中人物周围存在光晕现象。对比图6（a）～（h）可以看出，基于DWT、CT及文献[15]的方法所得融合结果在左侧大写字母P 的边缘较为模糊，且存在虚影。对比图7（a）～（h）可以看出，基于DWT、CT的方法所得融合结果在白色背景区域存在模糊噪声点现象，文献[18]结果的中上部分靠近车把附近有白色亮斑出现。而本文算法所得融合结果并未出现上述虚影和噪声现象，并有效地保留了源图像中的聚焦部分和细节信息，整体视觉效果最佳。

为了进一步说明本文算法的有效性，选取六种常用的客观图像质量评价指标对各算法的融合结果进行定量分析，它们分别是信息熵（Information Entropy，IE）、空间频率（Spatial Frequency，SF）、标准差（Standard Deviation，SD）、平均梯度（Average Gradient，AG）、互信息[19]（Mutual Information，MI）和边缘保持度[20]（edge preserving degree，QAB/F）。

信息熵IE反映了图像包含信息的多少，其定义为：

其中，L 为灰度级数，pi表示灰度为i 的像素数占图像总像素数的比值。

标准差SD体现了图像灰度相对于整体平均灰度的离散分布情况，其定义为：

其中，F(i,j)为融合图像，大小为M×N ，μ 为图像像素的均值。

平均梯度AG刻画了图像边缘细节的保持程度，定义为：

其中，ΔFx,ΔFy分别表示图像在x,y 方向上的差分。

空间频率SF是一个只对像素灰度值阶跃敏感的图像评价指标，其大小反映了图像灰度的变化快慢，其定义为：

其中，RF,CF 分别表示图像的行频率和列频率，计算如下：

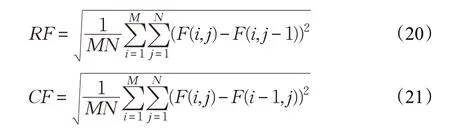
互信息MI的大小衡量了融合图像与两幅源图像的相关程度，其定义为：

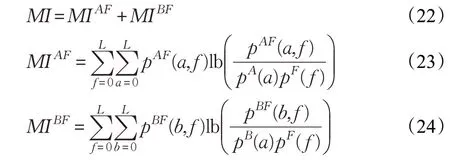
其中，pX(x)表示图像X 的概率密度函数，pXF(x,f)表示源图像X 与融合图像F 的联合密度函数。

边缘保持度QAB/F用于衡量由源图像转移至融合图像中的边缘细节信息的多少，定义为：

其中，ωX(i,j)表示图像X 的边缘强度，(i,j)和(i,j)分别表示融合图像F 相对于源图像X 的边缘强度和方向保留度。上述指标对各算法的评价结果如表1～4所示。

从表1～4 可以看出，在四组实验结果中，本文算法的六个客观指标值均处于中间位置。同时，没有一种算法在所有指标上均取得最大值，甚至连标准图像也只在极少几个指标上取得最优。另外，除了标准图像的空间频率在四组实验中都取得最大以外，其他各指标在四个实验中的最大值都不是由同一个算法取得。以上分析表明单一的客观评价指标很难直接区分融合算法的优劣。通过进一步分析，发现评价指标的优劣并不能完全反映融合图像视觉效果的好坏。例如，在Group1中，文献[15]方法虽然在信息熵和平均梯度上取得了最大值，但其融合结果（如图4（d）所示）在左上角有条纹状噪声；文献[18]方法的标准差虽然取得了最大值，但其融合结果（如图4（g）所示）在左侧钟表的边缘处有明显的虚影模糊现象。在Group2中，CT方法虽然在平均梯度上取得了最大值，但其融合结果（如图5（c）所示）在人物头部周围存在光晕现象；文献[18]方法的信息熵虽然取得最大值，但其融合结果在人物头部周围存在明显虚影（如图5（g）所示）。同样的结果也出现在Group3、Group4中。

表1 Group1客观评价指标

表2 Group2客观评价指标

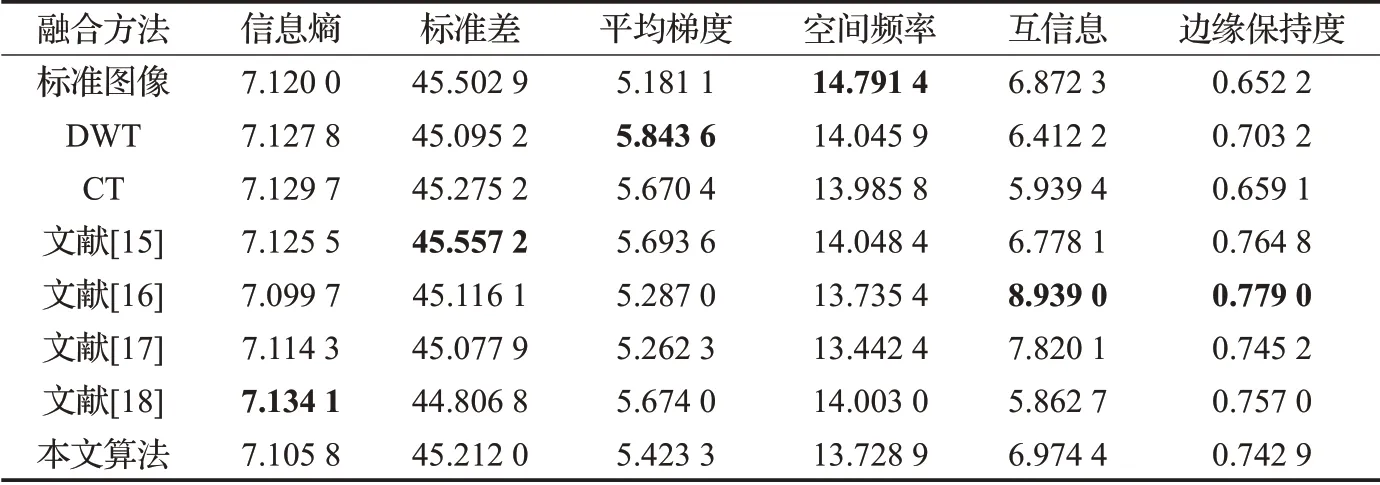
表3 Group3客观评价指标

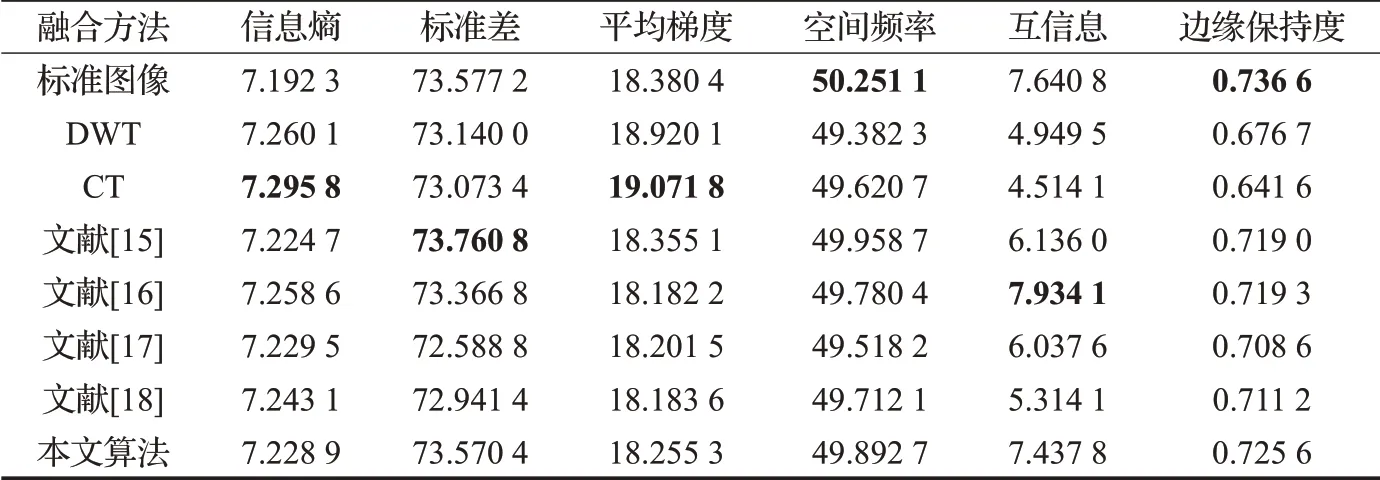
表4 Group4客观评价指标

由上面的分析可知，这些评价指标虽然常被用来对融合结果的质量进行定量分析，但是其数值的大小并不能十分准确地反映融合结果的优劣。其原因在于，第一，图像融合领域目前并没有公认的客观评价指标，想要定义一个符合人眼视觉特征的无参客观评价指标依旧是一件很困难的事情[21]；第二，客观评价指标在很多情况下会与主观评价相违背，无参评价指标所评估的结果有时会与人眼视觉感知不符[22]，比如：一些视觉感知上有明显模糊、虚影、颜色失真的图像，其客观评价指标反而较高[19-20]。

为了充分利用以上6种客观评价指标，减少单一评价指标的误判，本文以标准图像为参照定义了一种新的融合图像评价指标，称为融合效果偏差（Fusion Effect Deviation，FED）。相对于本文所选6 种评价指标，第i种算法的融合效果偏差，记为FEDi，定义如下：

其中，i=1,2,…,7 分别表示对比实验中的7 种融合算法，表2中第一列从”DWT”到”本文算法”依次为第1种至第7种算法。 j=1,2,…,6 分别代表6种客观评价指标，表2 中第二行从”信息熵”到”边缘保持度”依次为第1个至第6个评价指标；FEDi,j表示第i 种算法相对于第j 种指标的融合效果偏差；st 代表标准融合图像；ei,j表示第i 种算法所得融合结果的第j 个评价指标值，est,j表示标准图像的第j 个评价指标值。显然，FED 值越小，其融合图像与标准图像越接近，融合效果越好。

为了更直观地区分算法优劣，对于两组图像基于多种算法融合结果的客观评价指标分别计算FEDi,j，并以堆积条形图的方式展示，如图8所示。

由图8可以看出，本文算法具有最小的融合效果偏差FED。这说明本文算法在融合聚焦区域、保留边缘和细节信息、保持与源图像相关程度的同时，能够更准确地完成融合任务，是一种有效的多聚焦图像融合算法。

图8 融合效果偏差的堆积条形图

表5 列出了不同融合算法的平均耗时。对比发现本文所提算法的效率处于中等，比文献[15]、文献[16]和文献[17]算法的时间开销小，但比DWT、CT以及文献[18]算法的运行时间长，其原因可能是融合规则太复杂。然而，虽然本文算法比DWT、CT以及文献[18]算法的复杂度高，但有更好的融合效果和客观评价指标。

5 结语

本文针对多聚焦图像融合问题，提出了一种自适应可协调经验小波变换，使其适用于图像间相匹配的多层次分解表示。并将其作用于多聚焦图像，通过对C-EWT分解所得的高频分量和低频分量分别设计合适的融合规则，得到了一种新的多聚焦图像融合算法。实验结果表明，本文所提算法无论是主观视觉效果还是客观指标评判，都取得了好的结果，是一种简单有效的融合方法。本文还利用多种客观评价指标构造了一种新的评价指标——融合效果偏差FED，该指标能较好地对图像融合效果进行评价，本文方法在四组实验中均取得了最优的FED 值。将EWT 方法应用于多聚焦图像融合中，不仅增加了图像融合的手段，而且也扩展了EWT 的应用领域，对EWT 自身的发展也将具有一定的促进作用。如何对信号的Fourier谱自适应地进行分割是EWT的关键之一，下一步工作将根据信号的特点探索更优的Fourier谱自适应分割方法，得到改进的EWT分解，同时考虑将本文算法拓展至彩色图像融合领域。

表5 不同融合算法的耗时比较