基于形态学及区域合并的分水岭图像分割算法

李云红，张秋铭，周小计，贾凯莉

西安工程大学 电子信息学院，西安710048

1 引言

图像分割是图像分析、图像识别和图像理解的基础，图像分割质量的好坏直接关系到后续图像处理的效果，故图像分割在图像处理过程中占据着十分主要的地位。图像分割是利用图像的灰度、颜色、纹理、形状等信息按照标准将图像中具有特殊含义的不同区域分开。保证被分开的每个区域内部满足一致性，区域与区域间满足一定差异性。图像分割可以从复杂场景中提取出人们感兴趣的目标，然后进行下一步处理。

目前主流的图像分割方法包括阈值分割、基于区域增长的分割、分水岭分割[1-2]、聚类分割和神经网络分割等。分水岭算法是建立在数学形态学理论基础上的基于区域的图像分割方法。分水岭算法起源于Digabel等对简单二值图像的分析，20 世纪70 年代末，Beucher 和Lantuejoul为增加模型的适用范围提出应用分水岭算法进行图像分割，1991年Vincent等[3]提出了基于浸沉技术的分水岭分割算法，为后续的分水岭分割研究提供了基础，但早期方法负担重、耗时过长的问题尤为显著。近几年，对分水岭算法的研究和改进也在进一步深入中。王栋等[4]提出一种基于分水岭和FLICM 模糊聚类的图像分割方法，能够有效地解决过分割问题，但对于一般图像噪声的效果不明显，易造成失真现象。陈洁等[5]通过提取标记点进行分水岭图像分割，但只能在一定程度下抑制过分割。林振荣等[6]使用形态学滤波对图像平滑降噪，再对分割后图像区域合并，有效保留了图像的重要轮廓信息，但缺乏对复杂图像的适用性。形态学分水岭[7-11]由于其对区域边缘定位和封闭轮廓提取具有较好的效果被广泛应用在图像分割中，但普遍存在过分割问题。基于标记的分水岭分割算法[12-13]具有一定先验性，分割结果依赖于标记选取，选取不同的标记与图像分割的结果密切相关。

针对以上图像分割算法存在的诸如对图像细节噪声敏感、分割过程出现过分割等问题，提出基于形态学标记及区域合并的分水岭改进算法。该算法能够有效抑制分水岭的过分割，同时也能弥补传统形态学标记的漏标记区域问题。

2 传统分水岭算法

传统分水岭原理图如图1所示，分水岭算法（watershed）的基本思想是将图像看作为地理学的拓扑地貌，将图像想象成一个立体的地形表面。图像中的每一个像素的灰度值作为该点的海拔高度，每一个局部极小值及它影响的区域被称为集水盆，则集水盆的边界就形成了分水岭。分水岭的概念和形成能够通过模拟浸入的过程来说明，假设在每个区域极小值的位置刺穿一个小孔，从孔中向该区域不断注水，则地势较低的区域会首先被淹没，在浸入加深的过程中，每一个局部极小值的影响域都处在慢慢扩展过程中，当水淹没到一定高度时两个集水盆会相连合并为同一个区域，此时应在两个集水盆汇合处构筑“大坝”来阻止区域合并，最终形成分水岭，这些“大坝”的边界对应于分水岭的分割线，同时也是由分水岭算法提取出的连续边界轮廓。

图1 传统分水岭原理图

2.1 分水岭算法步骤

根据传统分水岭的原理，用M1,M2,…,MR表示分割图像g(x,y)的最小值点的坐标集合，G(Mi)为一个点的坐标集合，这些点位于与Mi相关系的集水盆内。图像g(x,y)的最小值和最大值分别用min 和max 来表示。

式中，T[n]表示坐标g(s,t)中点(s,t)的集合，这些点都位于平面g(x,y)=n 的下方。水位增加过程中，观察xy平面会产生一幅二值图像Cn(Mi)，可表示为：

算法初始选取C[min+1]=T[min+1]，随后算法进行递归调用，假设C[n-1]已经建立，根据C[n-1]求出C[n],Q 代表T[n]中连通分量的集合，对每一个q ⊆Q(n),有以下几种可能性：

（1）q ∩C[n-1]为空；

（2）q ∩C[n-1]包含C[n-1]中一个连通分量；

（3）q ∩C[n-1]包含C[n-1]中至少一个连通分量。

当获得一个最小值符合条件（1），此时将q 并入C[n-1]构成C[n]；q 位于最小值构成的集水盆中时，满足条件（2），重复（1）中操作；满足（3）条件C[n-1]时，q含有一些组成的元素，此时需在q 内建立一座水坝，防止单独集水盆内溢流溢出。

2.2 分水岭分割效果

按照传统分水岭图像分割算法步骤对医学CT图像进行分割处理，CT 图像如图2 所示，处理结果如图3 所示。发现传统分水岭算法虽对微弱的边缘具有良好的响应，但对图像中噪声、物体表面细微的灰度变化比较敏感，噪声会恶化图像梯度进而造成分割结果轮廓偏移，通常的分割结果会出现严重的“过分割”现象。为得到更好的图像分割效果，必须对分水岭算法进行改进。

图2 CT图像原图

图3 传统分水岭分割

3 形态学区域合并的分水岭算法

3.1 算法步骤

（1）形态学混合开闭重建运算

数学形态学是以结构元素为基础对图像进行数学分析的工具。在数学分析过程中利用具有一定形态结构的结构元素度量和提取图像中的对应形状，进一步达到对图像识别和分析的目的，在图像的处理过程中，有四种数学形态学的基本运算：膨胀，腐蚀，开运算和闭运算。

图像腐蚀能够使小于结构元素的物体，小的凸起或毛刺被去除，通过选取不同尺寸大小的结构元素，能够在图像中去掉不同大小的物体。膨胀操作能够将图像变大，填充物体内部的孔洞。

在形态学中，结构元素是最基本的概念。结构元素在形态变换中所起到的作用相当于信号处理中的“滤波窗口”。用B(x)代表结构元素，对于工作空间E 中的每一个点x，腐蚀和膨胀操作定义如式（3）、（4）所示：

对于图像，腐蚀膨胀操作定义如式（5）、（6）所示。

其中，f(x,y)为输入图像，b(x,y)为结构元素。先腐蚀后膨胀的过程为开运算，用来平滑较大物体的边界同时不改变物体面积。先膨胀后腐蚀的过程为闭运算，能够填充物体内部孔洞连接邻近物体，平滑边界的同时不改变其面积。由于噪声和细节可能位于目标信号的上方或下方，使用单一的腐蚀或膨胀操作，只能消除目标信号上方或下方的噪声和细节，且平滑后的图像总是位于原图的上方或下方，因此会造成目标信息的位置偏移。构建形态学开闭混合运算，能够在保持目标信息完整性和位置不变的前提下，达到消除图像中细节噪声的目的。此步骤能够在后续处理之前，消除梯度图像中由于非规则灰度扰动和噪声引起的局部极值，保留目标物轮廓和信息。

（2）图像增强，拉普拉斯锐化处理

进一步强调图像的边缘和细节，对图像进行锐化，提高对比度。拉普拉斯锐化图像与某个像素的周围像素到此像素的突变程度相关，依据是像素的变化程度。根据二级微分能够找到像素的过渡程度。当邻域中心像素灰度低于它所在的邻域的平均灰度值时，此中心像素的灰度也应随之降低；当中心像素灰度值高于它所在邻域平均灰度值，中心像素的灰度值应该升高。以这种方式来实现图像的锐化。

二阶微分和像素的关系如式（7）所示：

拉普拉斯重心掩模系数为：

可得到四邻域矩阵模板（9）：

同理八邻域的锐化过程如式（10）所示，矩阵模板：

将得到的值替换原(x,y)像素处的值，能够得到类似边界的地方，由式（12）得到锐化图像：

（3）标记背景和目标物

在寻找标记时，目标物体相对较亮而背景对应暗区。若此时背景区域较暗，可以利用图像二值化，找到背景的对应区域确保外部标记符能够包含于背景中，由于目标物一般位于图像其他物体的突出位置，故目标物可能为局部区域像素值的最大区域，可以通过寻找局部区域极大值作为目标物体的标记符。寻找内外标记符过程如图4所示。

图4 寻找内外标记符

首先对图像进行基于重建的连续开闭操作产生图片区域极大极小值，对极大值点作为目标物进行标记。再对图像二值化对像素进行距离变换将像素点位置信息转换为图像的灰度信息。然后取出图像相邻区域的分界线构成背景标记，最后对图像的梯度幅值图像进行修正。

（4）基于最大相似度的区域合并（MSRM）

在上一步的标记结束后，仍存在部分遗漏的未标记区域。此方法能够合并遗留的区域到目标区域或背景区域中。MSRM分为两个阶段，第一阶段为采样迭代方式，未标记区域集合中与背景集合相似度较大区域与背景集合合并。直到在背景集合中不再有新区域与未标记集合的某个区域合并为止。在每个迭代步骤中，背景集合和未标记集合不断更新，背景集合扩张未标记区域集合收缩。第二阶段专注在处理第一阶段完成后剩余的区域，未标记区域集合中根据区域最大相似度先进行集合内区域合并，合并后区域属于目标物或者背景交由下一轮完成。两个阶段不断相继执行，直到没有新的区域合并为止。

①A 是B 的相邻区域，用SA=表示A的邻近区域，且B ∈

3.2 算法流程图

综上，算法流程图如图5所示。首先将获取的彩色图像转换为灰度图像，对灰度图像进行形态学开闭操作去除图像细小噪声，再用拉普拉斯强化轮廓。然后以图像区域的亮暗程度为前提标记图像目标物和背景区域，并对修正后的梯度幅值图像分水岭分割。最后利用MSRM对分割图像区域合并，将漏标记区域合并到目标物或背景区域中，直到没有新的区域合并成功算法结束。

图5 算法流程图

4 实验结果

为进一步测试改进分水岭算法的分割效果，实验在Intel 酷睿i7-7500U CPU，8 GB RAM 计算机完成。实验所用工具为MATLAB2016。对图6中Cameraman、Lena、Coin 经典图像和医学图像采用聚类图像分割算法，Hminima标记的分水岭算法[10]，Otsu类间最大距离分割算法和本文改进后的分水岭算法进行分割结果比较，图7为在Lableme中标记的GT图像，比较结果如图8～11所示。

图6 原始图像

图7 GT图像

图8 Cameraman图像分割结果比较

图9 Lena图像分割结果比较

图10 Coin图像分割结果比较

图11 医学图像分割结果比较

为进一步评价算法的分割效果，采用分割交并比（Intersection-over-Union，IoU）、精确度precision、召回率recall进行评价，分割交并比原理如图12所示，计算方法如式（13）所示。精确度，召回率计算方法如式（14）所示。

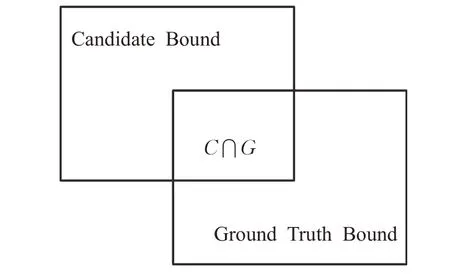
图12 IoU计算示意图

从图8～11 可以看出，本文算法对比聚类算法、Hminima标记的分水岭算法和Otsu类间距最大距离分割方法在图像细节的分割效果上具有一定优势。采用算法平均分割时间和分割交并比，精确度和召回率对几种算法进行量化比较，结果如表1～3所示。本文算法平均分割时间为2.63 ms，对比基于H-minima 标记的分水岭[14]、k 均值聚类[15]、Otsu 分割方法分别提升3.86 ms，2.88 ms，5.64 ms。如表2 所示分割交并比IoU 平均为96.42%，比其他算法平均值高出12.65%，2.77%和3.07%。算法平均精确度和平均召回率为0.921和0.922，对比其他算法针对4种图像的分割精确度平均值高出0.081，召回率高出0.088。

表1 算法平均分割时间对比 ms

表2 分割交并比IoU对比表 %

表3 精确度、召回率对比表

为了验证算法在复杂背景图片中的分割效果，又选取了几幅具有复杂背景的图像进行测试，原始图片13（a）、（b）、（c）来源Berkeley Segmentation Dataset[16]，图14 为在Lableme中标记的GT图像。分割结果与基于H-minima标记的分水岭算法、聚类分割和Otsu类间最大距离分割算法进行比较，比较结果如图15～17所示。经验证得出本文分割算法不仅适用于简单背景的常规图片，对具有复杂背景图像也具有较好的分割效果。通过观察轮廓提取结果，分割效果对比形态学标记分水岭分割有明显提升。

5 结论

图13 原始图像

图14 GT图像

图15 BSDS376001图像分割结果对比

图16 BSDS300091图像分割结果对比

图17 BSDS101087图像分割结果对比

基于形态学的连续开闭操作能够消除图像的细节噪声，再利用拉普拉斯锐化强化图像边界，使图像边界更加清晰。然后在此基础上标记图像目标物与背景并修正梯度幅值图像，对得到的梯度幅值图像进行分水岭分割。最后将初步分割结果进行MSRM 区域合并，使遗漏的标记区域合并到目标物或背景区域中。实验结果表明，改进后的算法对比聚类分割、Otsu 类间最大距离分割方法和增强细节的分水岭三种算法在分割精确度和平均算法分割时间上具有明显优势，且对于复杂背景图片的分割具有一定适用性，是一种有效的图像分割算法。