语言比例二元组Bonferroni平均算子的群决策方法

赵惠妍，李伯权，张 慧，李永义

1.安徽师范大学 数学与统计学院，安徽 芜湖241003

2.南京工业大学 交通学院，南京210009

1 引言

决策信息以语言变量形式给出的决策问题广泛应用于现实生活之中，如人事考核[1]、信息检索[2-3]、医疗诊断[4-5]等。在决策过程中，由于人类思维的模糊性、不确定性以及决策问题本身的复杂性，往往会直接给出定性的评估信息，因此，对该类问题的研究引起了学者的高度关注，目前，许多学者提出了不同的语言信息的集成方式，如基于扩展原理的近似计算模型[6-7]：该模型首先将语言信息转化为模糊数，再利用模糊数运算法则进行近似计算、基于符号的语言集成算子[8]、二元组语言模型[9-11]等等。其中，扩展原理和符号的两类语言信息集成会不同程度地造成决策信息的丢失，而二元组语言模型不易丢失决策信息，但计算颇为繁琐。如何使决策结果既精确又好算呢？

基于上述问题及研究基础，同时考虑到三角模糊数是将模糊的不确定语言转化为确定数值的一种方法，并且在信息集成过程中可以简化计算，通过借鉴扩展原理和二元组语言信息集成的决策方法，本文首先给出了三角模糊数的中心有序加权平均算子的概念，其次，在文献[12]的语言术语的数值表示（NR）的基础下，提出了将三角模糊数的中心有序加权算子替代语言术语的数值表示（NR）的方法，它比文献[12]中语言术语的NR更加精确，同时使语言决策计算过程更加好算，然后，考虑到语言比例二元组在集成过程中信息不易丢失，而Bonferroni平均算子能够很好地捕获输入变量之间的相互关联情况，可以将多个输入变量集结为一个输入变量，提出了语言比例二元组的Bonferroni平均算子的群决策方法，最后，通过球员择优的问题说明该方法的可行性。

2 预备知识

定义1[13]基本单位区间单调（BUM）函数g：[0,1]→[0,1]满足以下条件：

（1）g(0)=0；

（2）g(1)=1；

（3）若x ＞y，则有g(x)≥g(y)。

定义2 设A=(a,b,c)是三角模糊数[14]，由模糊集A的α -截集[15]定义可知，Aα可以写成Aα=[a+(ba)α,c-(c-b)α]，那么Aα的中心G(α)可表示为：G(α)=

3 三角模糊数的中心有序加权平均算子

定义3 对任意的三角模糊数(a,b,c)，且x ∈[0,1]，有Ax的中心，设g(x)是任意的BUM 函数，f(x)是g(x)的导数，即f(x)=g′(x)，则三角模糊数的中心有序加权平均（TFNCOWA）算子定义为：

注1 下面来解释一下上述定义中三角模糊数的中心有序加权平均（TFNCOWA）算子的合理性。

（1）离散情形，假设d1,d2,…,dn为区间按大小顺序任取的一列点，即b ≤dn≤…≤d1≤则令权重ωi由BUM 函数g 来表示，即ωi=，由BUM函数的定义，显然有)，且[0,1]，故ωi∈[0,1]，ωi=ω1+…+ωn=-g(0)]+…+[g(1)-g=g(1)-g(0)=1-0=0。

此时利用有序加权平均OWAg算子来集成n 个数据d1,d2,…,dn得：

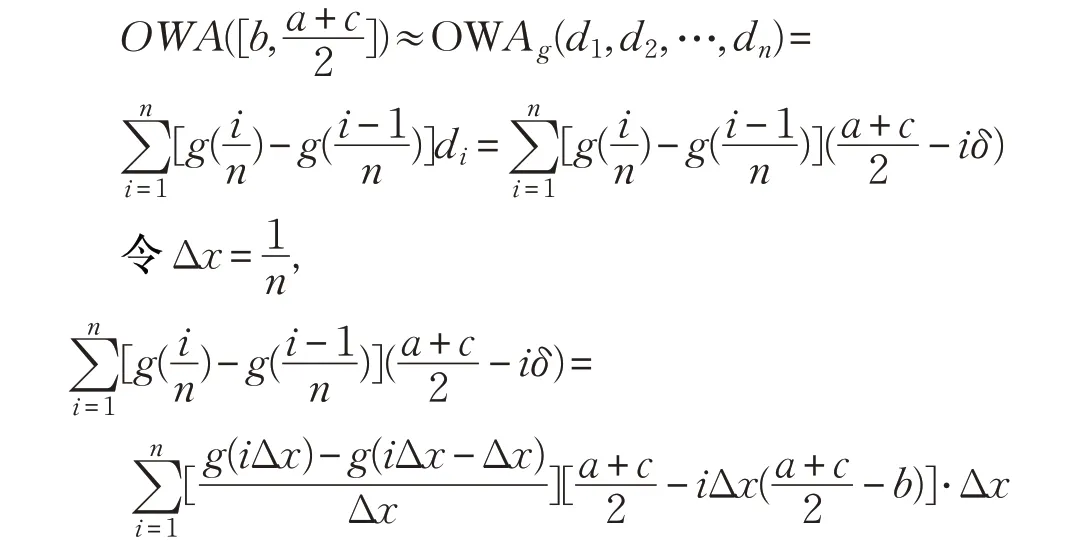
令n →∞,x=iΔx,i=0,1,…,n,x ∈[0,1]，对上式取极限，即得：

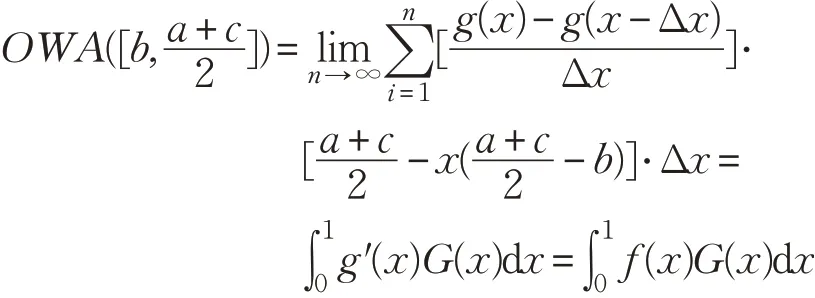
定理1 当取g(x)=xk(k ＞0)时，三角模糊数(a,b,c)的中心有序加权平均算子为：

证明对任意的x ∈[0,1],有Ax=[a+x(b-a),c-x(c-，取g(x)=xk(k ＞0)，得：

注2 当g(x)=-x2+2x 时，满足BUM 函数的三个条件，可以得到三角模糊数(a,b,c)的中心有序加权平均算子为：

注3 当g(x)=时，满足BUM 函数的三个条件，可以得到三角模糊数(a,b,c)的中心有序加权平均算子为：

4 基于三角模糊数的中心有序加权平均算子的语言术语的数值表示（NR）

在这一部分提出用三角模糊数的中心有序加权平均算子代替语言术语的数值表示（NR）的方法。

本文用区间[0,1]上的三角隶属函数来定义语言术语的语义。

语言术语集S={s0,s1,…,sg} 可以是等距的，也可以是不等距的。如图1和图2分别展示了等距语言术语集和不等距语言术语集的例子，当语言术语集是等距的时候，可以用三角隶属函数的核bi来表示一个语言术语si，如果语言术语集不是等距的，特别是语言术语集是不平衡的，在这种情况下，语言术语集的语言术语si主要是由核bi决定的，但是左宽li和右宽ri也会有一些影响，要解决这个问题，引入了文献[12]中的语言术语的数值表示（NR）。

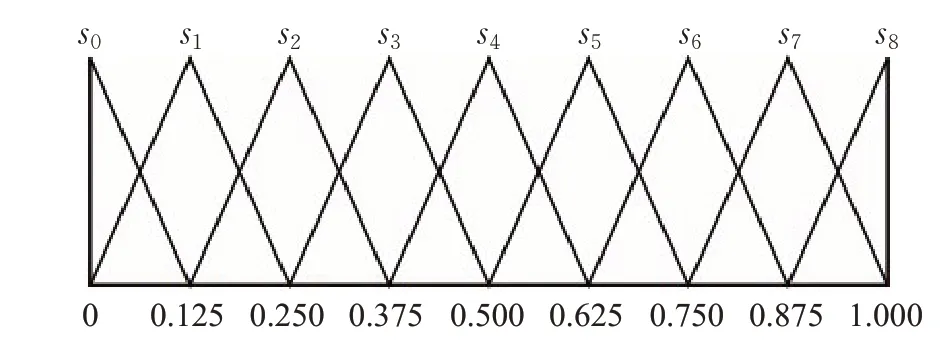
图1 等距语言术语集S={ }s0,s1,…,s8

图2 不等距语言术语集S={ }s0,s1,…,s4

定义4[12]设三角模糊数为Ai=(ai,bi,ci)，语言术语si∈S={s0,s1,…,sg} ，其中i=0,1,…,g,Ai是si的语义，li=bi-ai和ri=ci-bi分别称Ai或si的左宽度和右宽度，k1=-(θ-η)≤0，k2=η ≥0，其中θ-η 和η 分别表示li和ri的重要性，0 ≤η ≤θ ≤1，那么语言术语的数值表示（NR）定义为，NR：S →[0,1]，NR(si)=bi+k1li+k2ri。

由上可知，在等距语言术语集的情况下NR(si)=bi，在不等距语言术语集的情况下，特别是语言术语集是不平衡的情况下，NR(si)=bi+k1li+k2ri。

考虑到语言术语的数值表示与三角模糊数有关，并且三角模糊数的中心有序加权算子的几何意义和语言术语的数值表示的几何意义非常接近，那么语言术语的数值表示能否用三角模糊数的中心有序加权算子来计算呢?下面考虑几种情况：

（1）若g(x)=xk,则TFNCOWA((a,b,c))=·a+，假若可以得到

（2）若g(x)=-x2+2x,则：

通过这几种情况可以知道语言术语NR是可以通过三角模糊数的中心有序加权算子代替的。

为了方便计算，此处仅讨论g(x)=xk(k ≥0)的情形，可以发现利用三角模糊数的中心有序加权平均算子比文献[12]中求语言术语的NR更加接近语言术语的NR。

例1 设S={s0,s1,s2,s3,s4} 是语言术语集，如图2，语言术语集中的语言术语利用三角模糊数表示为：

s0=(0,0,0.5)，s1=(0,0.5,0.75)

s2=(0.5,0.75,0.875)，s3=(0.75,0.875,1)

s4=(0.875,1,1)

方法1 利用文献[12]中的模型(M-1)求解，得到θ*=1,η*=0.185，因此，语言术语的NR是：

NR(s0)=0.093 8，NR(s1)=0.058 2，NR(s2)=0.570 3

NR(s3)=0.796 9，NR(s4)=0.898 4

方法2 若s=(a,b,c)，则可以利用本文所得到的语言术语的数值表示（NR）的计算公式：

利用方法1得到NR(s1)=0.058 2，方法2得到NR(s1)=0.458 和NR(s1)=0.498，图2 中可以看出s1的数值表示是0.5，显然方法2中的结果更接近0.5，并且由图3可以发现，利用方法2（k 越大）算出的语言术语的数值表示更贴近例中的语言术语的数值表示。在此可以得到方法2比方法1好。

图3 语言术语的数值表示的比较

5 语言比例二元组Bonferroni平均算子的群决策方法

近年来，许多学者对语言比例二元组信息集成方式进行了研究，提出了不同的语言比例二元组信息集成算子，如比例二元组加权平均算子、比例二元组几何算子、比例二元组混合几何平均算子等等，这些算子在聚合过程中都是通过下标进行计算的，而语言项的语义（隶属函数）没有考虑，从文献[16]的结果中可知，上述集成方式适合等距的语言术语的聚合，如果语言术语是不等距的，特别是语言术语是不平衡的，这些算子的应用可能会导致不合理的结果，为了克服语言信息以LT2T 给出的形式的局限性，提出了语言比例二元组Bonferroni 平均算子。

定义5[17]设ai是非负实数，假设p,q ≥0，则Bonferroni平均算子被定义为：

定义6[16]设是语言术语集，对α ∈[0,1]，si,si+1∈S，称(αsi,(1-α)si+1)为语言比例二元组，记作LP2T，所有语言比例二元组构成的集合记为，即：

定义7 设S={s0,s1,…,sg} 是语言术语集，是所有语言比例二元组的集合，语言比例二元组的数值表示NR(αsi,(1-α)si+1)定义为，NR:Sˉ→[0,1]，NR(αsi,(1-α)si+1)=αNR(si)+(1-α)NR(si+1)。

因为NR(si),NR(si+1)∈[0,1]，可知：

NR(αsi,(1-α)si+1)∈[0,1]

定义8 NR的逆定义为，NR-1:[0,1]→Sˉ，NR-1(x)=(αsi,(1-α)si+1)，其中i 是由条件x ∈[NR(si),NR(si+1)]确定

定理2 LP2T的NR是单调的。

证明用LP2T 的比较规则[16]可证LP2T 的NR 是单调的。

定义9 设S={s0,s1,…,sg} 是语言术语集，Sˉ是所有语言比例二元组的集合，y1,y2,…,yn∈，语言比例二元组Bonferroni平均（LP2TBM）算子定义为：

LP2TBM(y1,y2,…,

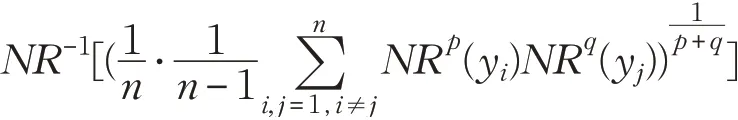
它具有下列优良性质：

（1）（幂等性）设yi∈Sˉ是语言比例二元组，若yi=y，i=1,2,…,n，则有：

LP2TBM(y1,y2,…,=y

（2）（单调性）设xi，yi(i,=1,2,…,n)是语言比例二元组，若对任意的i，xi≥yi，则有：

LP2TBM(x1,x2,…,xn)p,q≥LP2TBM(y1,y2,…,yn)p,q

（3）（有界性）设xi(i=1,2,…,n)是语言比例二元组，若x-=min{xi}，x+=max{xi}，则：

下面介绍一种语言比例二元组Bonferroni平均算子的群决策方法，具体步骤如下：

步骤1 对于某一语言多属性决策问题，假设A 和U 分别为方案集和属性集，决策者给出方案集是A={A1,A2,…,Am}，属性集是U={u1,u2,…,un}，专家集D={d1,d2,…,dt}，语言术语集S={s0,s1,…,sg}，是第k 位专家对方案ai∈A 在属性uj∈U 下的语言比例二元组，是决策矩阵，其中i=1,2,…,m ，j=1,2,…,n,k=1,2,…,t,计算方案ai∈A 在属性uj∈U下的语言比例二元组的NR。

步骤2 利用语言比例二元组Bonferroni 算子算出第k 位专家对方案评估的综合属性值其中i=

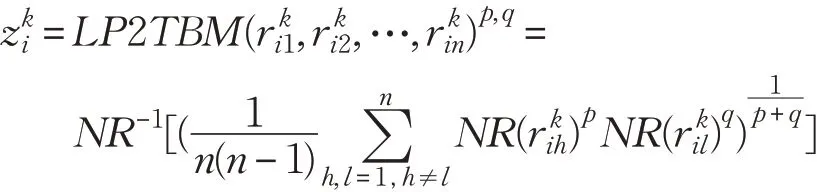
步骤3 再次利用LP2TBM 算子计算出t 位专家对方案Ai的综合评估值zi(i=1,2,…,m)：

步骤4 计算NR(zi)，并对NR(zi)进行排序，根据排序结果对方案进行择优。

6 案例分析

设某足球队有4 名后备球员，由于主力球员受伤，现在想从4 名球员中选择1 名球员参加比赛，用A={A1,A2,A3,A4}来表示4名球员，在对4名球员进行评估时，所要考虑的属性有u1（技术），u2（经验），u3（心理），用U={u1,u2,u3}表示，现请3位专家D={d1,d2,d3}对4位球员进行评估表示第k 位专家对方案Ai在属性uj∈U 下的语言比例二元2组，专家对球员的评价用下面的决策矩阵Rk=表示，设语言术语集S={s0,s1,…,s8}如图4所示。

图4 语言术语集S={ }s0,s1,…,s8

语言术语s=(a,b,c)，语言术语的NR的计算选用公式

计算出3个决策矩阵中语言比例二元组的NR：

利用LP2TBM 算子算出三位专家对4 名球员的综合属性值zki(i=1,2,3,4,k=1,2,3)，结果如表1所示。

表1 三位专家对4名球员的综合属性值

表1 三位专家对4名球员的综合属性值

再次利用LP2TBM 算子计算出各方案的综合评估值zi(i=1,2,3,4)：

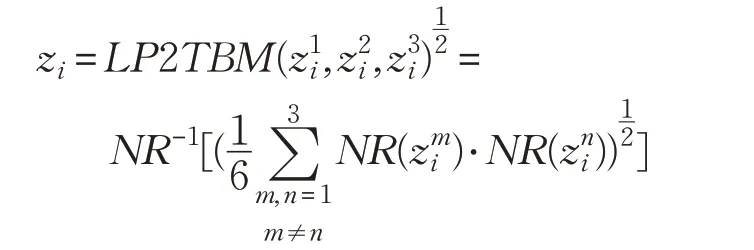
因此，z1=NR-1(0.425),z2=NR-1(0.415),z3=NR-1(0.458),z2=NR-1(0.426)。

因为NR(z1)=0.425,NR(z2)=0.415,NR(z3)=0.458,NR(z4)=0.426，可以得到：

NR(z3)＞NR(z4)＞NR(z1)＞NR(z2)

从而，相对于其他三名球员，第三位球员综合素质相对较好，应该选第三位球员A3参加比赛。

因为LP2T可以转化为L2T，而二元组OWA算子也是语言信息集成的一种算子，所以下面用二元组OWA算术平均算子的群决策方法来解决上面的案例问题。

步骤1 利用转换函数[12]：

将LP2T 决策矩阵R1,R2,R3转化为L2T 决策矩阵

步骤2 二元组OWA算术平均算子[9]：

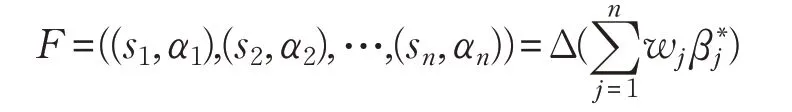
其中β*j是βi中第j 大的，βi=Δ-1(si,α)=i+α，通过二元组OWA算术平均算子算出三位专家对4名球员的综合属性值zki(i=1,2,3,4,k=1,2,3)，结果如表2所示，设属性权重w=(0.6,0.2,0.2)。

表2 三位专家对4名球员的综合属性值

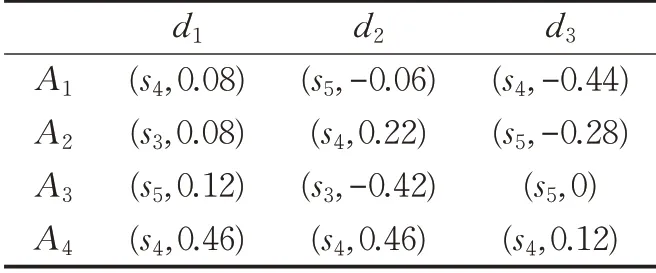
表2 三位专家对4名球员的综合属性值

步骤3 设专家的权重ω=(0.6,0.3,0.1)，再次利用二元组OWA 算术平均算子算出各方案的综合评估值Fi(i=1,2,3,4)：

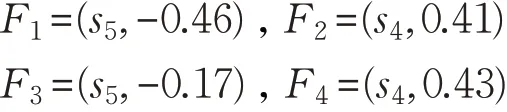
由二元组的比较规则[9]可知，F2＜F4＜F1＜F3，应该选第三位球员A3参加比赛。

由上可知最优方案是一样的，但排名不同，这是因为二元组OWA算术平均算子利用了L2T的下标进行运算，它没有考虑语言术语的语义。因此，它适用于等距的语言术语集，如果语言项不是等距的，特别是不平衡的，使用二元组OWA 算术平均算子会造成信息丢失。LP2TBM 算子利用了语言术语的NR，由于语言术语的NR 既适用于平衡的语言术语，也适用于不平衡的语言术语集，因此LP2TBM 算子既适用于平衡的语言术语，也适用于不平衡的语言术语集，另外，Bonferroni平均算子具有使聚合值之间相互增强的作用。故LP2TBM 算子将二元组的应用推广到更一般的语言术语集上。

7 结束语

在决策问题中，关于信息的集成问题，有时需要使用聚合算子来聚合信息，即聚合值在聚合过程中相互影响。本文将类似的思想应用到语言比例二元组环境中，首先定义了三角模糊数的中心有序加权平均算子。其次，利用三角模糊数的中心有序加权平均算子，对文献[12]中的语言术语的NR 进行了改进，并且用实例说明基于三角模糊数的中心有序加权平均算子得到的语言术语的NR更贴近语言术语的核的图像，验证了所提方法的可行性和合理性。为了克服语言信息以LT2T给出的形式的局限性，提出了语言比例二元组Bonferroni平均算子，并探讨了它的一些优良性质，进而提出了语言比例二元组Bonferroni 平均算子的群决策方法，最后通过实例验证了该方法的有效性和可行性。