基于脑网络和TSK模糊系统的癫痫脑电识别

杜 轻，辛守庭，雷新宇，于海涛

1.濮阳职业技术学院，河南 濮阳457000

2.安阳学院 航空工程学院，河南 安阳455000

3.天津大学 电气自动化与信息工程学院，天津300072

1 引言

癫痫是一种常见的脑部疾病，其特征是癫痫发作时脑区之间的异常电活动突然激增[1]，主要表现为脑电波（8～42 Hz）中棘波和尖波等特征波的出现，并且伴随有脑区之间过耦合现象的发生。癫痫发病率高，发作形式复杂多样，严重影响人们健康。目前癫痫的诊断主要依靠临床病史和对脑电图（Electroencephalograph，EEG）的直接观察。尤其对于临床诊断困难的非典型癫痫发作、各种异型癫痫和隐匿型癫痫来说，脑电图检测对该病的诊断起着至关重要的意义[2]。

癫痫脑电分析主要是对异常活动的检测，最重要的是识别脑电信号中是否出现棘波和尖波。国内学者采用多种方法检测癫痫特征，包括非线性滤波、模板匹配、拟态法等传统方法和小波变换、神经网络等新方法[3-7]。Arakawa 等设计了由预测滤波器和简单非线性函数组成的非线性滤波器，采用非线性滤波方法分离癫痫棘波[3]。朱勇等提出一种基于经验模态分解的癫痫特征波检测方法，该方法首先经过分解得到若干个固有模态函数，然后对其中第一个模态函数应用非线性能量算子进行特征波提取，从而达到癫痫棘波检测的目的[5]。此外，鉴于视觉检测存在费时、效率低等不利因素，建立了自动癫痫特征检测系统，通过长期动态脑电信号监视，检测出包含棘波的EEG段，进而减少误检率，该系统既可以用于在线检测，即检查脑电的同时，对棘波或尖波进行检测，也可用于检查后的离线数据分析[4]。此外，将人工神经网络等机器学习算法与癫痫检测相结合，利用其自适应和自学习能力，进一步提高特征提取和识别的准确率。初孟等提出一种将时-频域分析与Jensen函数相结合的方法进行棘波检测，提取出棘波的波形特征，并通过人工神经网络进行进一步的判决，从而降低棘波检测的误检率[7]。

癫痫脑电信号的发作模式往往存在着非线性、多样性和不确定性。为此，国内外学者提出采用现代信息处理方法来分析和提取癫痫发作时的脑电特征，包括关联维数、最大李亚普诺夫指数、LZ 复杂度、相关密度法和递归图分析方法等[8-14]。如李红利等采用排序互信息对癫痫脑电进行了同步性的分析，结果表明癫痫患者左脑区域内、右脑区域内及左右脑区之间的信息交流明显增强[9]。Guo 使用小波变换的近似熵特征，并结合人工神经网络对癫痫发作的EEG 信号进行分类[10]。李艳艳等结合Hilbert 变化提出了一种基于频率的Hjorth 参数移动性与复杂度，并将改进的Hjorth参数特征与二阶差分样本熵相结合作为癫痫脑电的融合特征[13]。采用上述方法识别癫痫信号的准确率较高，用于检测癫痫发作情况。

大脑是由不同脑区构成的复杂网络，其功能的发挥需要多个脑区相互作用、相互协调，同样癫痫可以网络的方式在不同脑区之间传播[15]。因此，从脑功能网络的角度来研究癫痫发作是极为必要的。近年来，随着复杂网络理论的快速发展，对网络的研究有着丰富的理论基础，把脑电时间序列映射到脑网络逐渐成为研究热点[16-20]。王若凡等通过有限穿越可视图构建癫痫发作前、中、后三种状态的脑网络，发现三种状态下构建的复杂网络具有不同形态的拓扑结构，发作中时更接近于规则网络，与发作前、后相比，在高频带下发作中网络的平均最短路径减小，而在低频带显著增大，且网络的复杂度明显降低[16]。柳真艳通过研究颞叶癫痫患者脑网络功能及结构的变化对致痫灶的定位提供更正确的依据[17]。研究表明，虽然患者的脑功能网络是变化且具有一定差异，但是其整体表现出共同的特征，它能够描述癫痫状态下不同脑区之间信息传递机制，是识别癫痫脑电信号的一种更高效的方法。

癫痫发作分为部分性/局灶性发作、全面性发作以及不能分类的发作等，由于在癫痫检测中缺乏对各类发作均有效的生物标志物（即标记系统结构和功能变化的生化指标），国内外学者提出采用机器学习方法用于异常脑电信号识别[21-30]。相比于人工标记脑电信号，机器学习方法能更快速有效地实现对癫痫脑电信号的识别[31]。目前，多种机器学习方法被应用于癫痫脑电信号的识别中，如支持向量机、长短期记忆网络、朴素贝叶斯法、线性判别分析法及模糊系统建模方法。柳长源等通过提取癫痫脑电的波动系数和近似熵等特征，提出了一种基于粒子群算法优化支持向量机参数的脑电信号分类检测技术[21]。Guler等以脑电信号的小波变换系数和Lyapunov 指数为特征，用于训练多类支持向量机，发现其将特征映射到更高维度的空间，在应用于癫痫识别时，表现出较好的性能[22]。单绍杰等基于脑电图数据，利用长短期记忆网络的神经网络模型和提取的单导联脑电小波能量特征对癫痫发作进行分类，取得了98.5%的分类精度和零误警的结果，在精度上和泛化能力上都要优于传统的支持向量机等方法[23]。但是，上述研究主要是利用特定频段获得的单导联脑电信号，分析局部脑功能状态，无法反应整个大脑的活动情况。因此，本文提出利用多导联脑电信号的相关性，构建具有全局特性的脑功能网络，用于分析大脑的整体活动特征，并将其与机器学习算法相结合，识别癫痫脑电信号。

在目前主要的智能识别方法中，模糊系统不仅具有较好的可解释性，还能以任意精度逼近任意函数，较之其他方法具有独特的优势[31]。模糊系统是在模糊规则中引入模糊集合和模糊逻辑，将语言形式的模糊表达转化成数学形式的不确定表达式。经典模糊系统包括Mamdani-Larsen（ML）模糊系统，广义模糊模型（GFM）模型和由Takagi等人提出的Takagi-Sugeno-Kang（TSK）模糊系统[32-39]。其中，TSK 模糊系统由于其良好的可解释性和强大的学习能力，广泛应用于识别与预测领域。如Shams 等提出了基于减法聚类的TSK 模糊建模方法来区分类自闭症谱系障碍和估计预后的程度，识别准确度在80%～100%[38]。Zhang等通过TSK模糊规则构造了非线性自适应模糊逼近器，使计算复杂度和非线性建模能力得到良好的平衡，并且用于预测非平稳脑电时间序列和单导诱发电位[39]。本文将脑功能网络和模糊系统相结合，构建癫痫患者的脑功能网络，以脑网络参数为输入，建立TSK模糊系统模型，并通过监督式学习训练分类器，准确识别癫痫发作期的脑电信号。

2 方法

本文结合脑功能网络和TSK模糊系统的方法，实现癫痫脑电信号的识别。系统框架如图1所示，通过相位同步指数（Phase Synchronization Index，PSI）估计导联之间的功能连接，构建癫痫病人的脑功能连接网络，并且提取脑功能网络的常用拓扑特征参数。采用TSK 模糊系统，以脑网络参数为TSK模糊系统的输入特征，通过监督式学习训练识别癫痫脑电信号。

图1 癫痫发作期EEG信号识别框架

2.1 脑功能网络

功能连接网络构建包括网络节点设置和节点间连接强度计算两个部分，把每一个电极定义为网络节点，通过PSI衡量任意两导联之间的功能连接。PSI可通过如下公式求得：

根据PSI邻接矩阵，通过设置阈值方法构建脑功能网络。建立具有一组节点（表示脑的信息处理中心）和连边（表示脑区之间的信息传递）的几何模型以表示脑功能网络。本文研究无权网络的拓扑结构特性，节点之间的关系是二值的，即有连边时值为1，无连边时值为0。脑功能网络的拓扑性质可以通过一些拓扑结构参数来表征，本文讨论采用的统计量为全局效率、局部效率、聚类系数、节点介数和边介数。

对于一个包含N 个节点的网络G，节点i 和节点j之间的连接为aij（有连接时aij=1，无连接时aij=0），最短路径长度表示网络中从一个节点到另一个节点最短路径的边数，它反映了网络内整体信息传输的效率。节点i 的平均最短路径定义为：

其中最短路径长度lij为：

网络G 的平均全局效率为：

局部效率和聚类系数是衡量由节点i 的相邻节点构成的子网络的紧凑程度，体现网络的局部信息传输能力。节点i 的局部效率定义为：

其中Gi表示由节点i 的相邻节点构成的子网络，NGi是子网络Gi所包含的节点数。网络G 的平均局部效率为：

节点i 的聚类系数定义为：

其中，Ki是节点i 的度，ti是节点i 与其相邻节点之间形成的三角形连接的数量，分别计算如下：

网络G 的聚类系数为：

介数是指以经过某个节点或连接的最短路径的数目来刻画其重要性的指标，从信息流的角度出发定义节点的中心程度。节点或连接的介数衡量了网络中节点之间沿着最短路径传输信息的控制能力。它的定义如下：

其中，pij(k)是节点i 和节点j 之间经由节点或连接k的最短路径数目，pij表示节点i 和节点j 之间最短路径的数目。

2.2 TSK模糊系统

TSK型模糊系统包括一组if-then模糊推理规则、模糊化器、推理算法和去模糊化器。在模糊系统中，模糊集合表示语言值，同时模糊逻辑规则也是用模糊集合来描述。对一个包含K 条规则，每条规则有d 个前件的TSK模糊系统，第k 条的模糊推理规则可进行如下表达：

其中，x1,x2,…,xd是前件输入变量，同时也是后件中的变量，A(i,k)(i=1,2,…,d)为第k 条规则高斯前件模糊集合。 yk表示第k 条规则的输出变量，是对输入变量的线性函数，β(i,k)(i=0,1,…,d)是线性参数。

其中隶属度函数表示为：

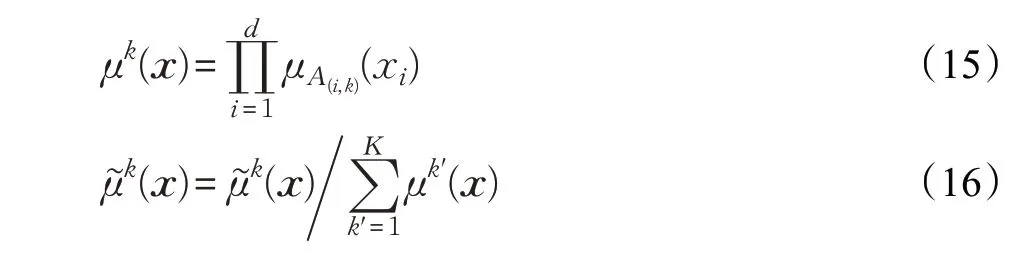
将高斯函数作为隶属度函数，则μk(x)可具体表示为：

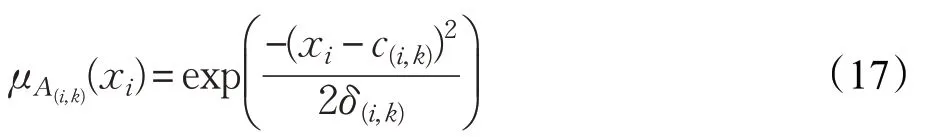
其中，参数c(i,k)及δ(i,k)通过经典的聚类算法或其他模糊空间划分方法来获取。本文采用模糊c-均值聚类算法（Fuzzy c-Means，FCM）进行前件的规则筛选与参数确定，c(i,k)及δ(i,k)可通过如下表达式求得：

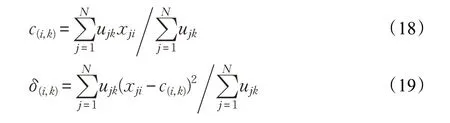
其中ujk表示输入向量隶属于第k 类的隶属度。因此，根据：

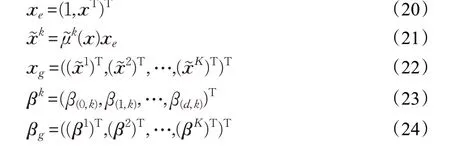
最终，TSK模糊系统的实值输出表示为：

2.3 TSK模糊系统

本文采用岭回归来确定后件参数，岭回归法又称吉洪诺夫正则化法，是由美国学者Hoerl 提出的一种改进的最小二乘估计法[40]。基于岭回归的后件参数优化过程如下：对于指定回归任务，首先构造训练数据集，其中xi是第i 个样本的d 维输入向量，yi是第i 个样本的C 维标签向量（当样本i 属于第j 类时yij=1，否则yij=0），NS是训练集样本总数，C 是数据分类的类别数量，本文实验只区分发作期和发作间歇期的EEG 信号，故C=2。构造模型的优化目标函数如下：

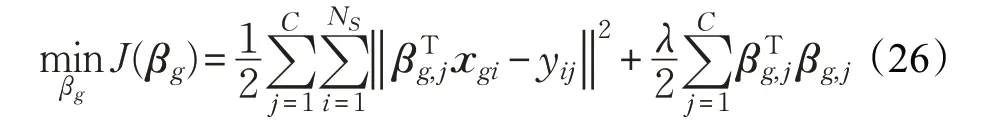
其中，xgi表示第i 个样本通过式（22）转化而来的向量，λ 为岭参数。通过求解，可得到βg,j的最优值为：

3 实验

3.1 数据采集

在本次实验中，共有25例确诊的被试癫痫患者（其中男性11例，女性14例，年龄为21～36岁），所有参与者均为右利手，并且没有其他精神或神经系统疾病以及任何其他严重疾病。本实验研究已通过当地伦理委员会批准。所有受试者均由其本人均在签署知情同意书的情况下，自愿参加了本实验。

对于每个被试，在几天内采集15～25 次的EEG 信号，每次采集时间为一小时。总共记录数据次数437次，其中包含109 次癫痫发作。在采集期间，要求被试者坐在半昏暗安静的房间里，闭眼并保持清醒，避免如抬手、眨眼等肢体动作。本实验使用Phoenix 数字脑电系统来记录脑电信。极帽电极放置位置遵循国际标准的10-20系统，数据记录为19个顶部电极（Fp1，Fp2，F7，F3，Fz，F4，F8，T3，C3，Cz，C4，T4，T5，P3，Pz，P4，T6，O1，O2）处的信号。脑电采集放大器放大倍数为4 096，采样频率为256 Hz，分辨率为0.5 μV，脑电仪的带通滤波器的滤波范围为0.05～70 Hz。

3.2 数据预处理

在脑电图采集过程中，人体的生理活动会对脑电信号产生干扰，如眼电和肌电等，此外癫痫患者发病时的悸动也会造成干扰，导致获取的脑电信号含有多种频率的噪声和伪迹。因此，本文利用Daubechies（db）小波系列中的db4 小波进行8 层分解与重构，可以对脑电信号中存在的直流成分、缓慢基线漂移、高频噪声和伪迹等进行滤除，以获得符合算法要求的脑电数据。根据25例被试患者的EEG 信号的采集时间和癫痫发作次数，本文从每个患者采集的数据中随机抽取3 组癫痫发作期测得的EEG信号和3组发作间歇期测得的EEG信号，构成本次实验的数据集。实验中数据集分两组：（A）75例癫痫发作间歇期EEG信号；（B）75例癫痫发作期EEG信号。图2（a）和（b）分别为从A和B中随机选取的一组19导EEG信号。

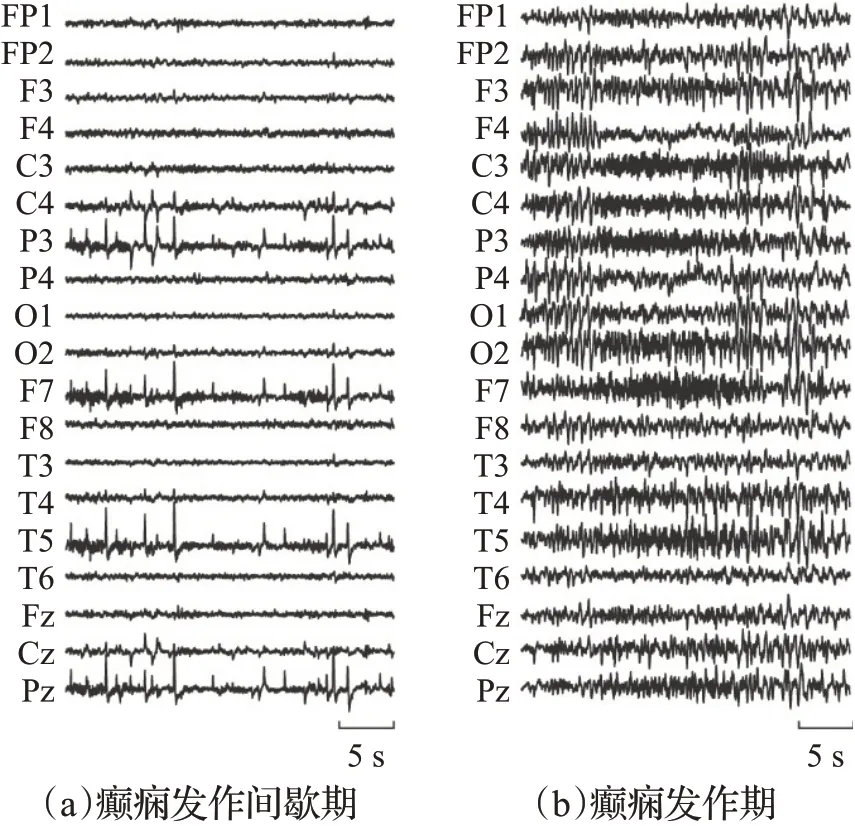
图2 EEG信号

3.3 实验结果与分析

本文在建立功能连接网络时以19个电极对应的大脑皮层位置作为网络节点，节点之间的连接强度通过计算PSI 估计，由此得到19×19 全连接的邻接矩阵。癫痫发作间歇期邻接矩阵的平均值（0.250 1）小于癫痫发作期（0.349 8），并且存在统计学差异。实验结果说明癫痫发作时脑区之间的功能连接强度更强，信息处理及交流效率也会大幅提升。选取合适阈值后，令邻接矩阵中大于阈值的连接为1，小于阈值的连接为0，从而构建无权脑功能网络，如图3所示。对A组和B组中每个对象构建功能连接网络，并且计算全局效率Eglobal、局部效率Elocal、聚类系数C、节点介数Bnodal和边介数Bedge等网络参数。实验结果表明，相比发作间歇期，癫痫发作期时的脑功能网络有更低的全局效率、局部效率和聚类系数，和更强的节点介数、边介数。因此，上述网络特征可以进一步用来识别癫痫发作。

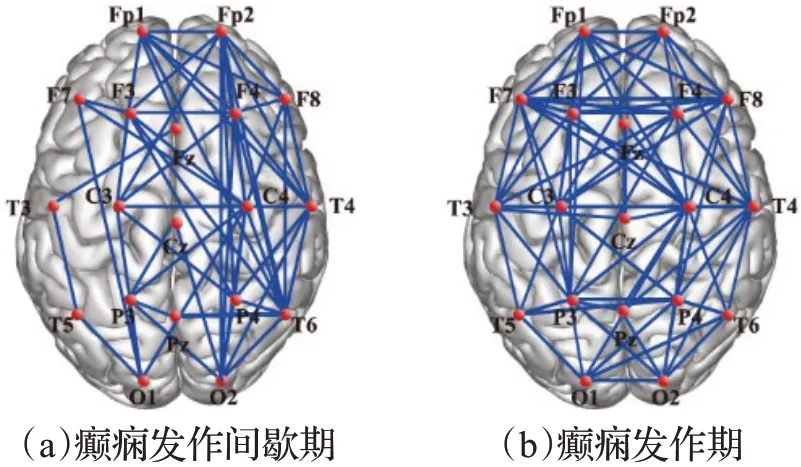
图3 脑功能网络

模型解释：在A组和B组选取一定数量的样本构成训练集，将提取的网络拓扑特征Eglobal、Elocal、C 、Bnodal和Bedge作为TSK模糊模型的输入，A组癫痫发作间歇期的EEG信号标记为[0 1]T，B组发作期的EEG信号标记为[1 0]T。根据公式（20）～（22），构建新形式的训练集。以使用5条模糊规则的TSK模糊模型为例，模糊语言描述分为5 个等级，分别为非常低、低、中、高和非常高，图4为五条规则中各前件的隶属度函数以及其对应的模糊集合（聚类中心c，平方差δ）。具体地，对全局效率Eglobal，规则1～5 的模糊聚类中心分别为：0.61，0.77，0.91，0.86，0.64。将其比较大小排序后可得各规则的模糊描述：规则1中Eglobal为非常低；规则2中Eglobal为中；规则3中Eglobal为非常高；规则4中Eglobal为高；规则5 中Eglobal为低。同理可得到规则中其他特征的模糊语言描述，并且由公式（23）～（26）优化得到规则后件参数。表1列出了所有5条模糊逻辑规则。

图5表示TSK模糊系统的识别结构，其输入的列向量癫痫发作期的脑功能网络特征（其组成分别为Eglobal、Elocal、C 、Bnodal和Bedge）构成，根据表1 的模糊规则和公式（25）可得，五条规则的分量输出之和yo=[0.98 0.03]T。将yo中最大的元素置为1，其余为0，从而得到最终决策输出是y=[1 0]T，表示系统正确识别出癫痫发作期的EEG 信号。此外，如图5 中所示，模糊规则1 的分量输出=[0.97 0.02]T相比其他的模糊规则更接近于[1 0]T，这说明模糊规则1 在识别过程中占主导地位，最终决策输出主要由模糊规则1决定。

为了验证分类器的有效性，本文通过多组实验来研究TSK 模糊系统被用于癫痫发作识别的性能表现。每组实验的训练数据集包含120个随机选择的样本（癫痫发作间歇期和发作期各60个），测试数据集由余下30个样本构成（癫痫发作间歇期和发作期各15个）。为研究分类性能，将利用准确度、敏感度、特异度来体现分类器的分类性能。实验结果如表2所示，当采用全部网络特征作为TSK模糊系统的输入时，TSK模糊系统性能为最佳：98.36%准确度、99.48%敏感度和97.24%特异度，表明使用的网络结构参数越多，分类器的识别能力就越强。此外，TSK模糊系统可以用来研究癫痫发作识别的最有效网络特征。同时采用全局效率Eglobal和聚类系数C 作为输入时的分类器表现优异：94.70%准确度、96.86%敏感度和92.54%特异度，其识别癫痫发作期EEG信号效果明显优于其他网络参数组合。因此，通过图示全局效率和聚类系数的联合分布来说明其有效性，如图6 所示，其中每个点代表一个样本。显然，癫痫发作期与发作间歇期存在显著的分布差异。

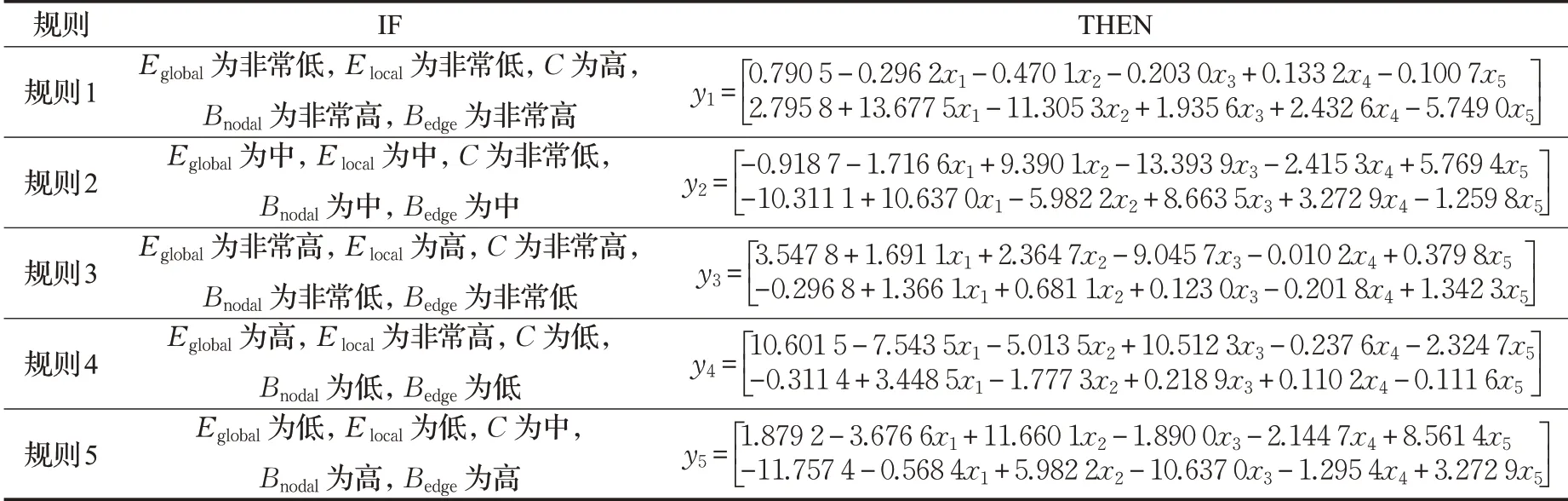
表1 模糊规则

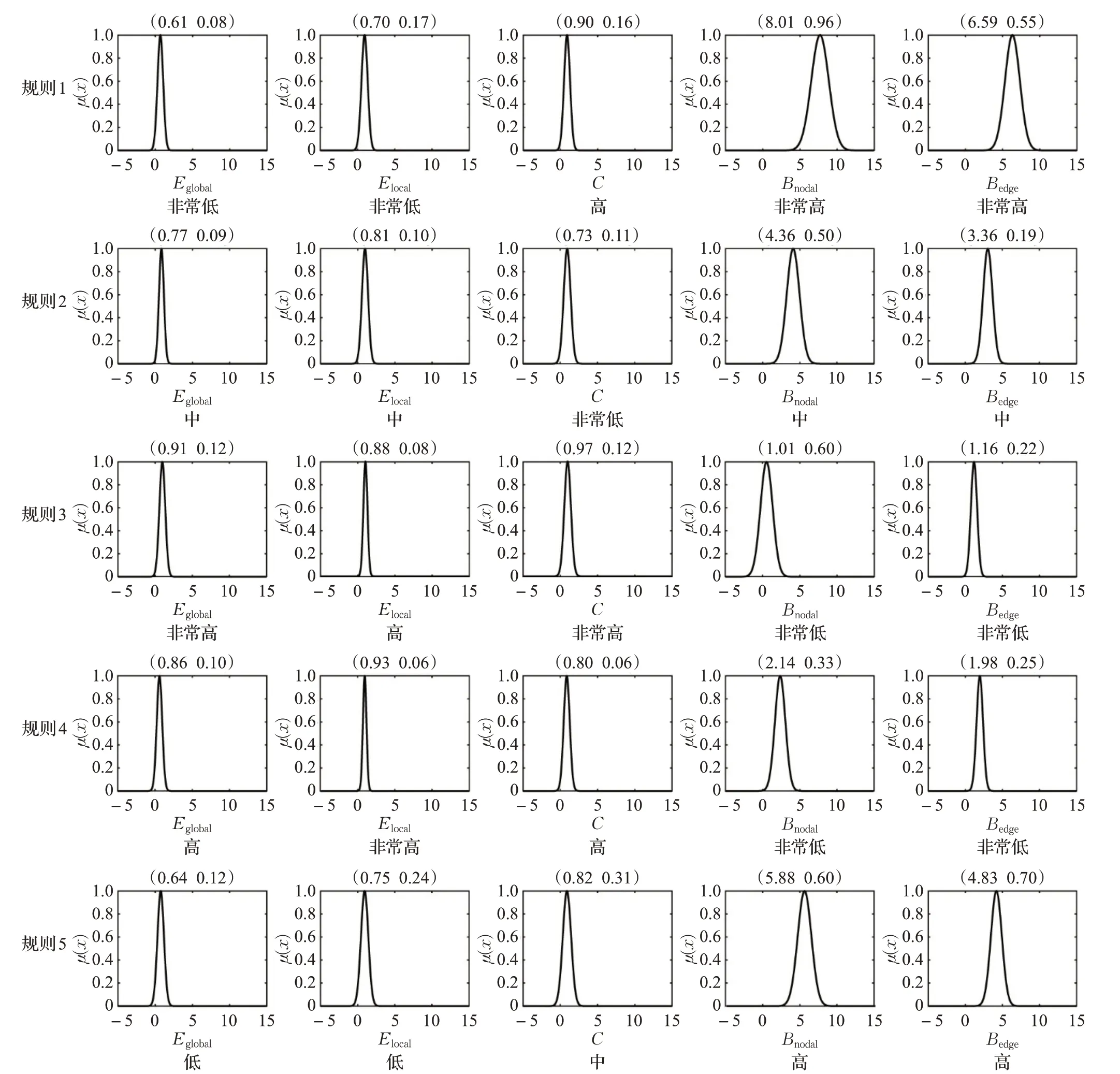
图4 规则前件中各变量模糊集合A(i,k)（聚类中心c，平方差δ）以及对应的隶属度函数和模糊语言描述

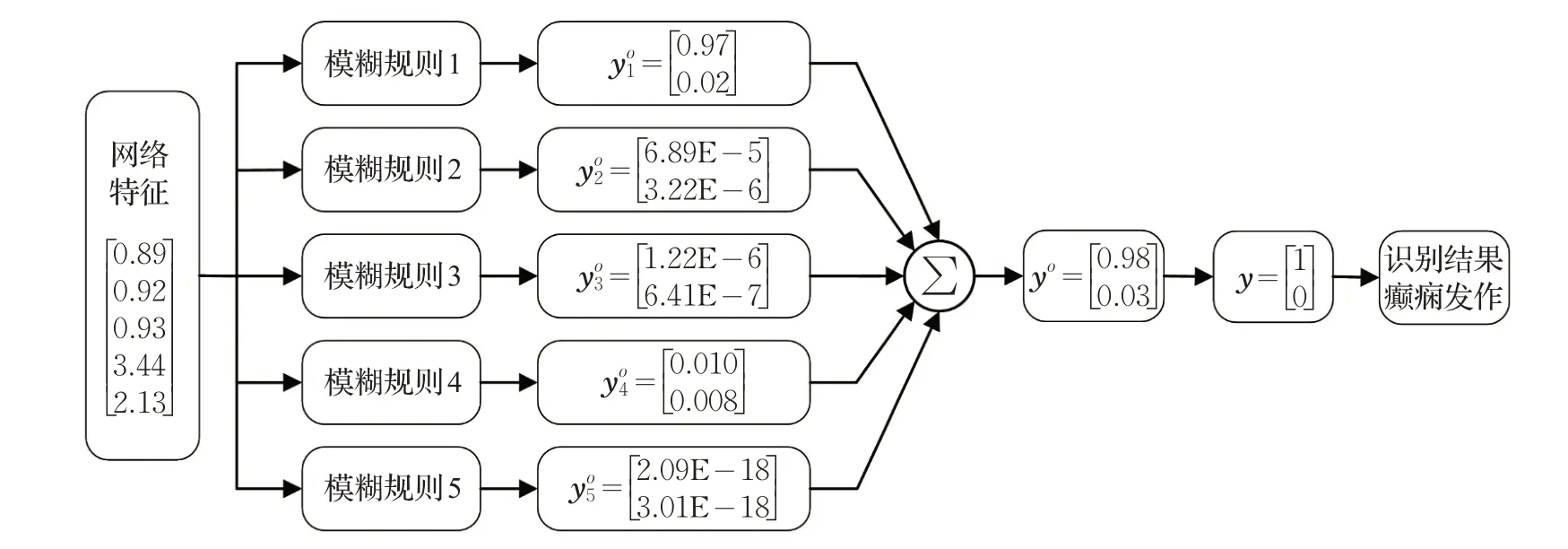
图5 TSK模糊系统的识别结构

表2 基于复杂网络的TSK模糊分类器的性能参数

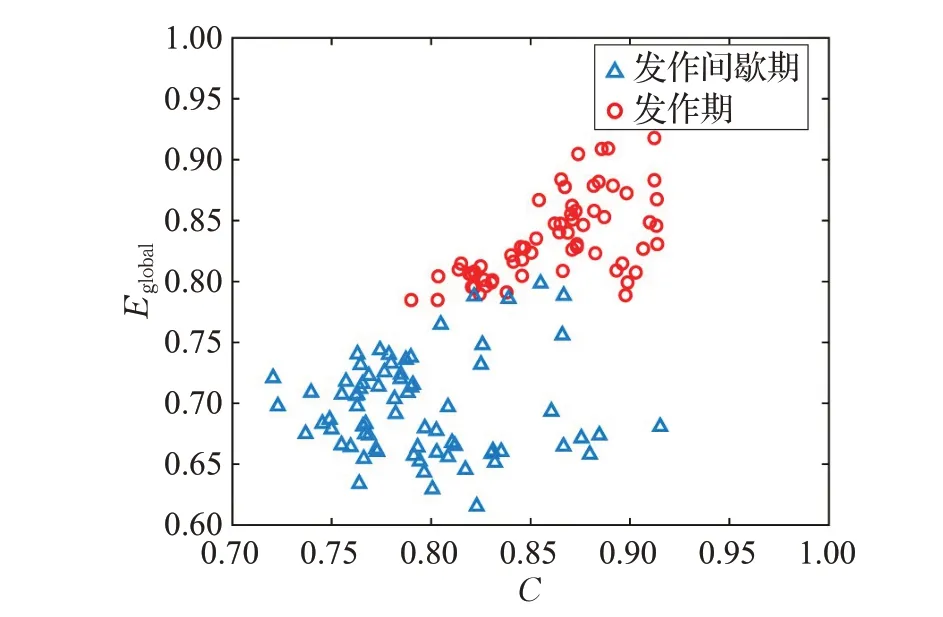
图6 全局效率Eglobal 与聚类系数C

进一步验证脑功能网络与TSK 模糊系统相结合方法，在癫痫脑电识别任务中的优势。采用已有方法提取癫痫脑电特征，包括小波包分解提取的各频带相对能量特征、核主分量分析提取的降维特征以及脑功能网络特征，并与支持向量机相结合识别癫痫发作脑电信号。分析结果如表3 所示，小波包分解的准确度为92.81%，核主分量分析的准确度为92.55%，基于脑功能网络特征的分类效果更佳，准确度可达到96.77%，表明脑功能网络特征更能体现癫痫发作脑电信号的特性。此外，基于脑功能网络的TSK模糊分类器有着最佳的分类性能，说明模糊分类器在识别癫痫发作脑电信号时更具优势。

表3 基于复杂网络的TSK模糊分类器的性能参数

4 结束语

本文提出脑功能网络结合TSK模糊系统的方法，用于识别癫痫发作期的脑电信号。通过构建脑功能网络，从全局角度刻画癫痫发作期间各脑区之间功能连接的异常变化，并提取多种特征参数刻画网络的拓扑结构特性。建立以脑网络参数为输入的TSK模糊系统，通过监督式学习训练分类器，完成识别任务。实验结果表明，本文所提出的模糊分类方法可以实现对癫痫发作期EEG信号的精准识别，TSK模糊分类器的准确度达到了98.36%、敏感度为99.48%和特异度为97.24%，而且网络结构参数越多，分类器的识别能力就越强。此外，全局效率和聚类系数对癫痫发作期EEG信号的识别效果优于其他网络参数。结果为通过EEG检测识别癫痫疾病提供了新方法。