基于深度确定性策略梯度的智能车汇流模型

吴思凡,杜 煜,徐世杰,杨 硕,杜 晨

(北京联合大学 a.智慧城市学院; b.机器人学院; c.北京市信息服务工程重点实验室，北京 100101)

0 概述

车流汇入是实际行驶中的常见情况,也是目前智能车研究中的热点问题。由于智能车的决策系统不能较好地应对车流汇入的情况,因此多数解决方案是等待主路行驶车辆通过后再执行下一步动作,如何在适当的时机汇入始终是研究者关注的重点。

随着机器学习在智能车领域的不断发展,一些机器学习算法也逐渐被应用于解决车流汇入问题。文献[1]建立了基于分类回归树的无人车汇流决策模型,但该模型需要数据标注,并且只能根据瞬时数据进行决策,不具备有效预测周围环境的能力。文献[2]建立了基于贝叶斯网络的汇入行为预测模型,该模型属于规则化模型,当环境中出现特殊情况时,汇入成功率较低。文献[3]采用非参数支持向量机(Support Vector Machine,SVM)方法预测各种汇入行为,虽然此方法相比于其他机器学习模型汇入成功率更高,但仍然是监督学习,其学习过程是静态过程,不能实现与环境的交互。

为弥补机器学习在智能车领域应用中存在的不足,研究者提出强化学习的概念。目前该技术已被成功应用于人工智能[4-5]、棋牌游戏[6]和分析预测[7]等方面,其中最为典型的代表为TD[8]、Q-learning[9]和SARSA[10],但这些算法都是针对离散状态和行为空间的马氏决策过程,即状态的值函数或者行为的值函数采用表格的形式存储和迭代计算[11]。如果状态值太多,会出现占用内存增大的情况,导致效率降低。为此,研究者进一步提出解决方案。文献[12-13]将卷积神经网络与Q学习[14]算法相结合,建立了深度Q网络(Deep Q-Network,DQN)模型[15]。文献[16]以DQN算法为框架搭建智能车汇入模型,获得了较高的汇入成功率,但该算法仍然采用离散动作空间,不能直接应用于连续空间,无法应对智能车实际速度控制变化。文献[17]提出一种用于解决连续动作预测的深度强化学习算法DDPG,该算法可以在连续动作空间中运行,解决动作离散化会丢失动作域结构信息的问题。

本文采用深度确定性策略梯度(Deep Deterministic Policy Gradient,DDPG)算法建模,将智能车汇流问题转化为序列决策问题进行求解,并通过仿真实验与文献[16]模型进行对比,验证该模型在实际应用中的可行性和高效性。

1 基于DDPG算法的汇流模型

DDPG算法是研究者在Actor-Critic(AC)[18]算法框架的基础上,使用DQN的经验回放[19]方法和构造双网络结构的方法对确定性策略梯度(DPG)算法改进的一种深度强化学习算法,其用于解决连续动作空间下的马氏序列决策问题。

在DDPG算法中,确定性策略被描述为在状态st下采取的确定动作值at,动作值函数被描述为在状态st中采取at之后的预期回报,分别使用参数为θμ和θQ的深度神经网络来表示确定性策略a=π(s|θμ)和动作值函数Q(s,a|θQ)。

对Critic网络而言,eval估值网络通过θQ数化的函数逼近,使用最小化损失来更新参数,如式(1)所示。

L(θQ)=Est～ρβ,at～β,rt～E[(Q(st,at|θQ)-yt)2]

(1)

其中:

yt=r(st,at)+γQ(st+1,π(st+1,θμ))|θQ′)

(2)

eval估值网络采用TD-error(梯度下降)进行更新:

(3)

对Actor网络而言,eval估值网络通过动作值函数将状态映射到指定动作来更新当前策略,状态回报定义为未来折扣奖励总回报:

(4)

本文通过Silver策略梯度的方法[20]对目标函数进行端对端的优化,从而以获得最大总回报为目的更新Actor网络参数，如式(5)所示。

(5)

DDPG算法采用经验回放方法对Actor-Critic双网络结构中的目标网络参数进行更新,通过将四元组(st,at,rt,st+1)存储在记忆库中,指定时间间隔,调用记忆库中的数据对目标网络参数进行更新:

θQ′←τθ+(1-τ)θQ′

(6)

θμ′←τθ+(1-τ)θμ′

(7)

其中,τ代表更新参数。

结合本文的汇流模型,DDPG神经网络结构如图1所示。

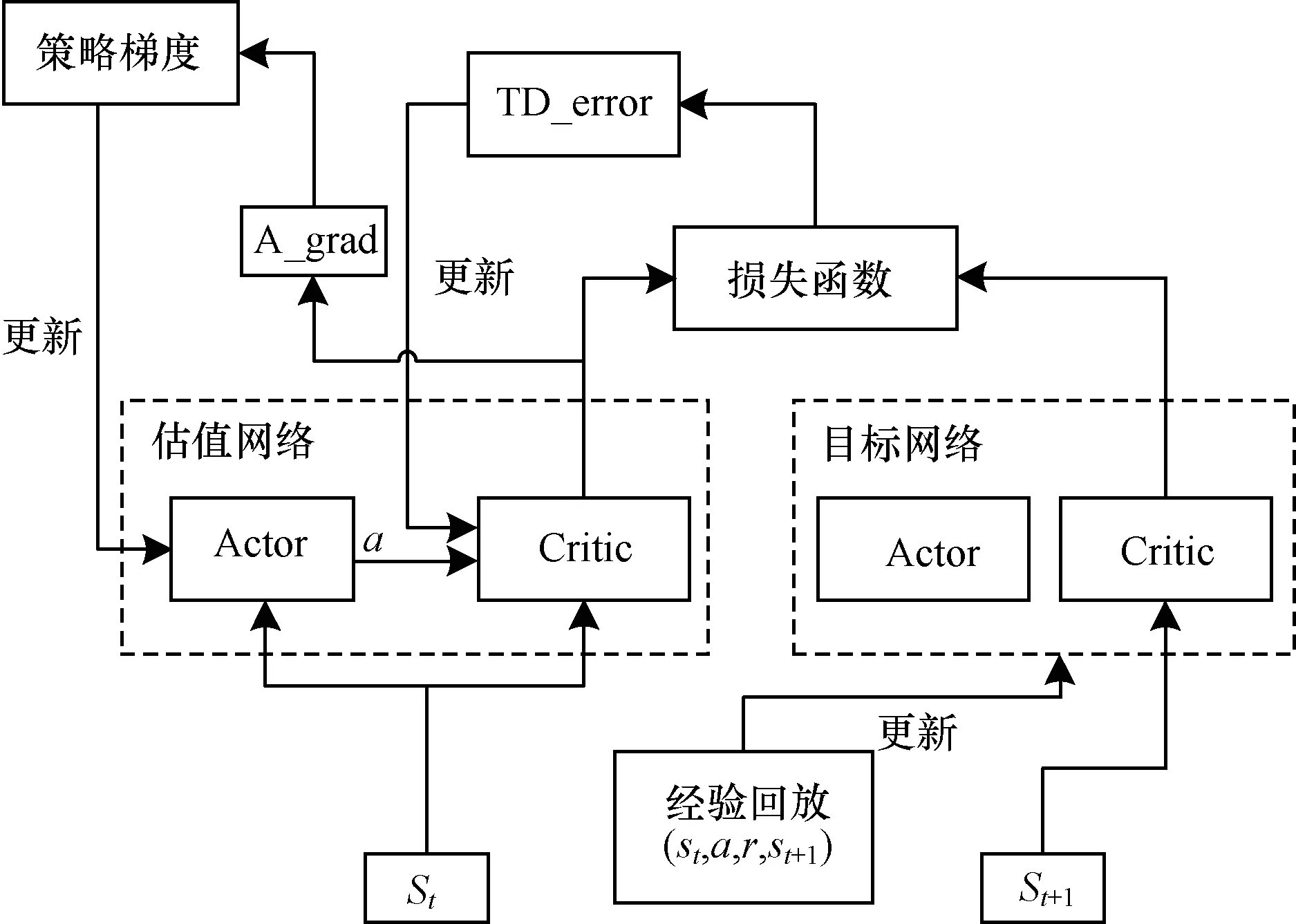
图1 DDPG网络结构

为探索汇入车流最优动作,筛选出更好的策略,本文通过在随机采样过程引入随机噪声N,从而获得at,如式(8)所示。

at=π(st|θμ)+N

(8)

其中,at的范围限制为[-5.5 m/s2,2.5 m/s2]。

网络中其他参数设置如表1所示。

表1 DDPG网络参数设置

2 汇流仿真环境

2.1 道路环境

本文以2017年“中国智能车未来挑战赛”无人驾驶智能车真实综合道路环境测试(城市道路)中一段匝道汇入口为对象,构建汇流仿真环境。该路段行车方向由南向北,其中主路分为3个车道,匝道为一个车道。主路实际长度约为700 m,每条车道实际宽度为3.75 m,主路限速为80 km/h,辅路限速为60 km/h。为简化仿真环境,消除一些无用信息,本文提取70 m主路道路作为仿真环境,如图2所示,其中汇入路口距初始位置约30 m。其他道路环境参数如表2所示。

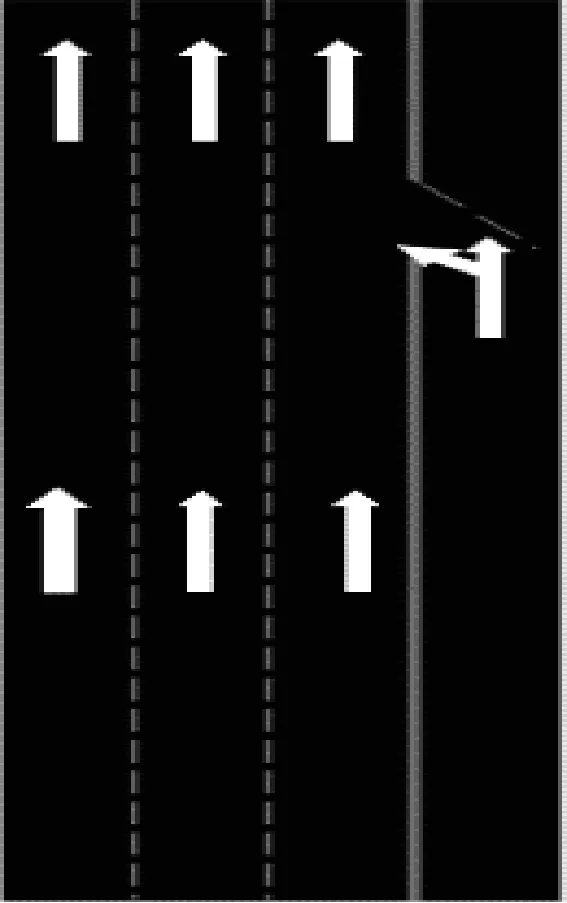
图2 道路仿真环境

表2 汇流环境参数设定

Table 2 Traffic merging environment parameter setting

环境参数参数值主路长度/m700.00主路限速/(km·h-1)80.00匝道限速/(km·h-1)60.00主路最低限速/(km·h-1)10.80车道宽度/m3.75汇入口宽度/m6.00环境刷新周期/s0.10

2.2 仿真车辆建模

本文以北京联合大学研发的“京龙六号”作为环境车(主路车)与代理车(匝道汇入车)进行建模,如图3所示。“京龙六号”自改装于北汽ex260轿车,车身长度约为4.1 m,车身宽度约为1.8 m,车顶配置32线激光雷达和GPS天线,车头安装4线激光雷达和毫米波雷达,后备箱装有车载导航系统。

图3 “京龙六号”实车

本文假设环境车辆只在车道3的主路行驶,车道1、车道2没有车辆行驶,代理车通过匝道入口时,汇入车道3,并且代理车的行驶轨迹按照制定的轨迹行驶,如图4所示。

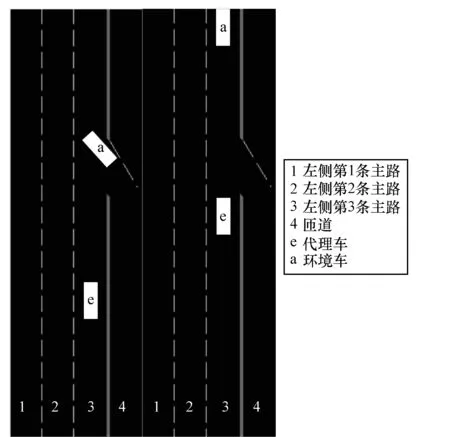
图4 匝道环境示意图

2.3 约束条件

根据对汇流情况的研究,本文将汇入状态分为加速和减速2种状态,采用与文献[14]相同的状态四元组空间进行描述:s=(车辆横向间距,车辆纵向间距,代理车车速,环境车车速),横/纵距离=环境车辆重心到代理车辆重心的距离(假设车辆的密度是均匀的),其中车辆横向距离、纵向距离由雷达数据所得,动作空间a用来描述车辆在行驶过程中瞬时加速度。加速度采用“京龙六号”实车测量数据,范围为[-5.5 m/s2,2.5 m/s2]。为使车辆在保证安全的情况下尽快汇入主路,采取单步惩罚-0.1。车辆碰撞条件为当车辆横向距离小于2.2 m,纵向距离小于安全值,安全值计算公式为:

(9)

其中,v1为环境车车速,v2为代理车车速,D为最小反应距离,D取值2.0 m。环境车车速和代理车车速由车辆传感器数据测得。

3 仿真与结果分析

本文将车辆汇入模型转换为在代理车(匝道车)与环境车(主路车)状态完全可观察下通过DDPG算法采取适当的汇入动作问题。在每步(时间间隔为0.1 s)代理车通过传感器接收观测值s(包括车辆横向间距、车辆纵向间距、代理车车速、环境车车速),采取动作a(加速汇入/减速汇入),并获取奖励r,经验池数据为(s,a,r,s_),其中s_表示下一步状态值。

模型建立后,本文根据现实过程中主路车辆行驶状态,即加速行驶、减速行驶、匀速行驶对模型进行训练。根据主路车辆行为,代理车辆采取相应的对策。实验环境采用python3.6进行环境模型建立,使用Tensorflow搭建神经网络框架进行回合训练,最大回合数为5 000回合。同时,为加快训练速度,对于强化学习算法每个回合探索的最大步骤进行限制,限制值为200步。

3.1 训练与测试结果分析

训练主要验证在车辆汇入时代理车辆是否学习到应对环境车辆车速变化所采取的汇入对策。通过每100回合记录在训练过程中汇入成功率描述该模型在应对不同环境车速时采取策略是否可行。

应对现实过程中主路车辆速度变化,本文将环境车速度变化分为匀速行驶、匀加速行驶和匀减速行驶3种主路车速度变化状态,环境车速度分为以下3种情况(车辆初始位置距汇入口30 m处)。

1)代理车辆初速度定为12 m/s(43.2 km/h)～15 m/s(54 km/h)内某个随机值,环境车初速度为12 m/s(43.2 km/h)～15 m/s(54 km/h)内某个随机值,训练结果如图5所示。

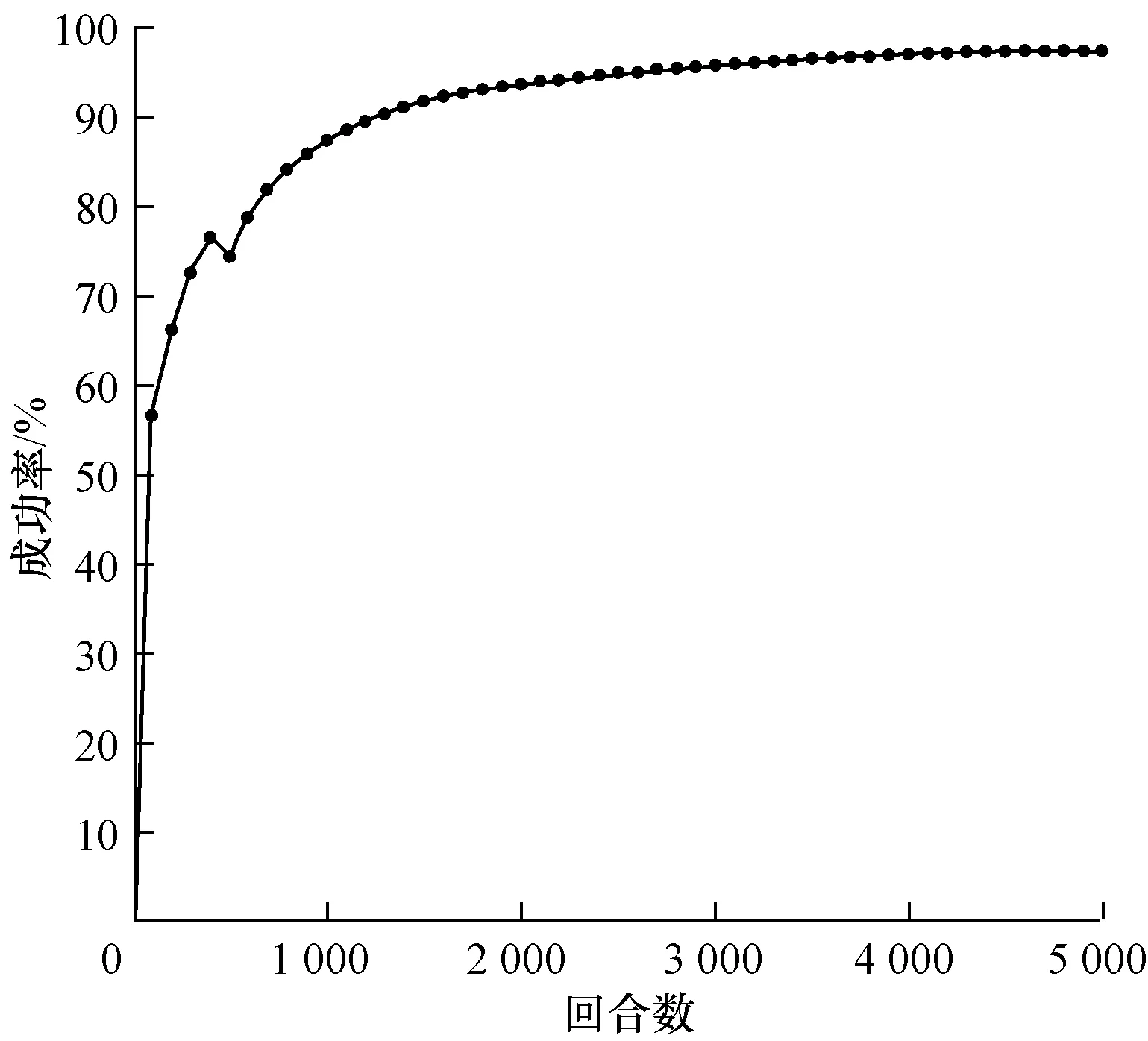
图5 环境车匀速行驶汇入成功率

Fig.5 Merging success rate of main-road vehicle at a constant speed

2)代理车辆初速度定为12 m/s(43.2 km/h)～15 m/s(54 km/h)内某个随机值,环境车初速度为12 m/s(43.2 km/h)～15 m/s(54 km/h)内某个随机值,且加速度选取(0,2.5 m/s2]内某个随机值,训练结果如图6所示。

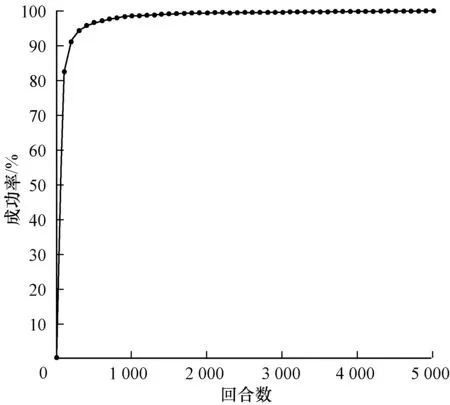
图6 环境车匀加速行驶汇入成功率

Fig.6 Merging success rate of main-road vehicle with uniform acceleration

3)代理车辆初速度定为12 m/s(43.2 km/h)～15 m/s(54 km/h)内某个随机值,环境车初速度为12 m/s(43.2 km/h)～15 m/s(54 km/h)内某个随机值,且加速度选取[-5.5 m/s2,0)内某个随机值,训练结果如图7所示。

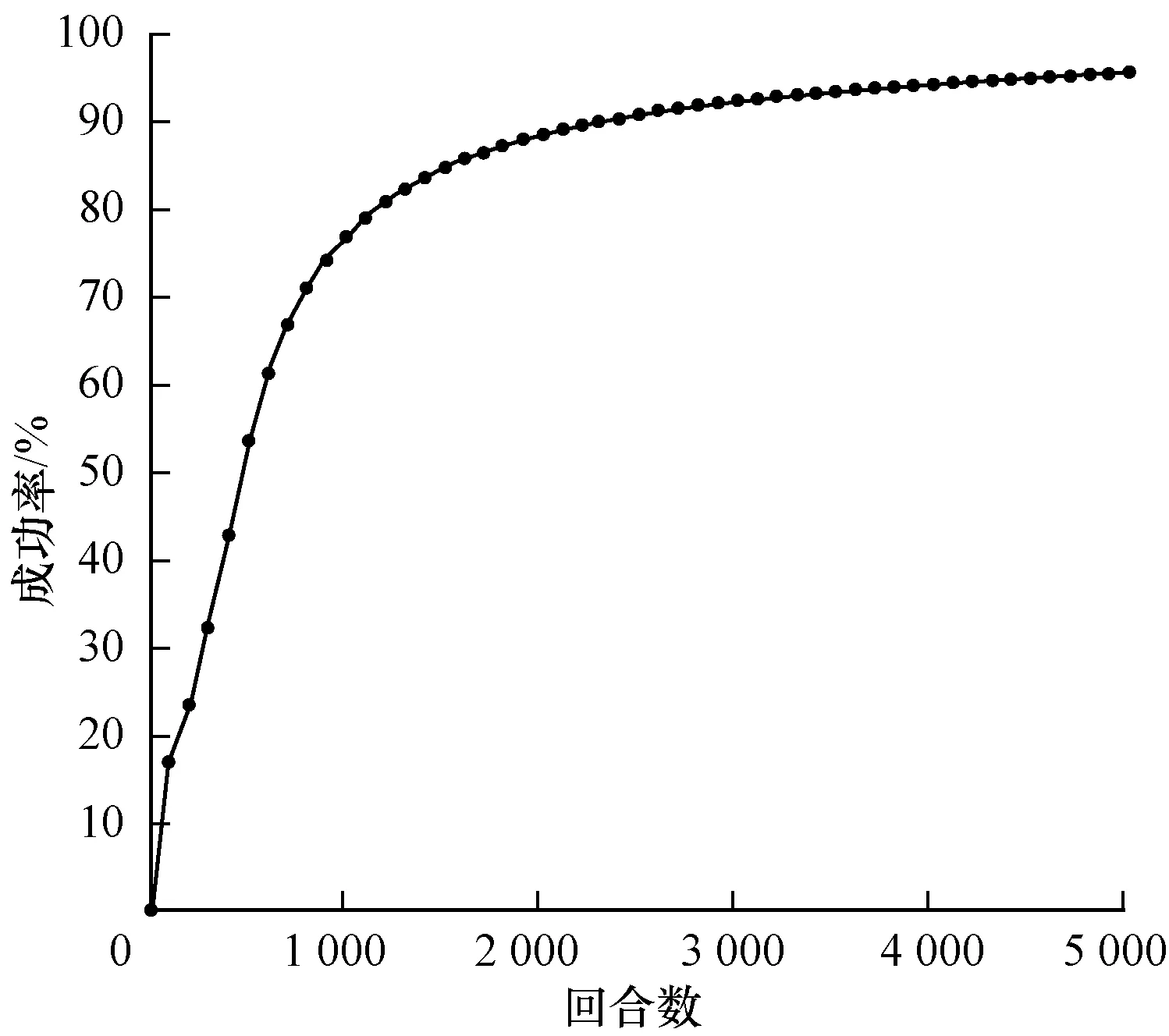
图7 环境车匀减速行驶汇入成功率

Fig.7 Merging success rate of main-road vehicle with uniform deceleration

在环境车匀速行驶状态下,车辆碰撞在500回合以后不再发生,模型达到收敛,并最终在5 000回合时成功率达到95%。在环境车做匀加速行驶的状态下,车辆汇入模型在前100回合时汇入效果已十分理想,并且最终成功率接近100%,在环境车做匀减速行驶的状态下,在前500回合成功汇入成功率不足45%,经过训练,在5 000回合时,汇入成功率达到95%。

实验测试3种不同环境加速度(-1.8 m/s2、0、2 m/s2)下代理车决策行为,测试结果如表3所示。

表3 不同环境车速下的测试结果

Table 3 Test results of main-road vehicle with different speeds

环境车车速代理车决策行为匀速行驶先减速后加速汇入以2 m/s2匀加速行驶减速汇入以-1.8 m/s2匀减速行驶加速汇入

当环境车辆匀减速行驶时,代理车为尽快汇入,采取的策略是不等待环境车通过汇入口后再通过,而是全程加速通过。当环境车在主路匀速行驶时,由于两车的初始速度几乎相同,在保证安全的情况下,此时代理车学习到的策略是先减速行驶,在保证一定安全距离后加速汇入。在环境车做匀加速行驶时,此时代理车为了安全汇入,不发生车辆碰撞,学习到的策略是减速汇入,等到环境车通过汇入口后,再汇入车流。

3.2 与文献[16]模型的实验结果对比

文献[16]利用DQN算法通过离散动作空间描述动作变化状态,使用单一目标网络储存参数产生目标Q值,并利用单估值网络产生单估值Q值,根据两者差异通过梯度下降更新网络参数。

对本文模型与文献[16]模型采用相同的四元组空间描述状态、环境参数以及网络训练参数。加速度变化范围为[-5.5 m/s2,2.5 m/s2],分别对3种环境车速度变化(匀速、匀加速、匀减速)进行对比,对比结果如图8～图10所示。

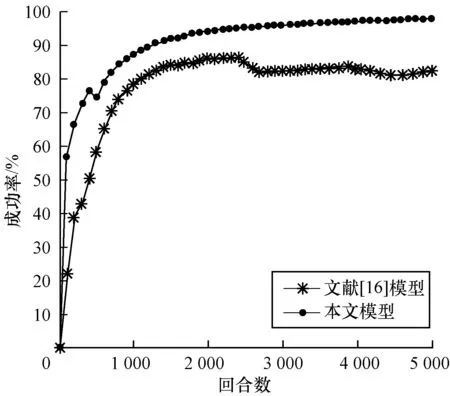
图8 环境车匀速行驶时的汇入成功率对比

Fig.8 Merging success rate comparison of main-road vehicles at a constant speed

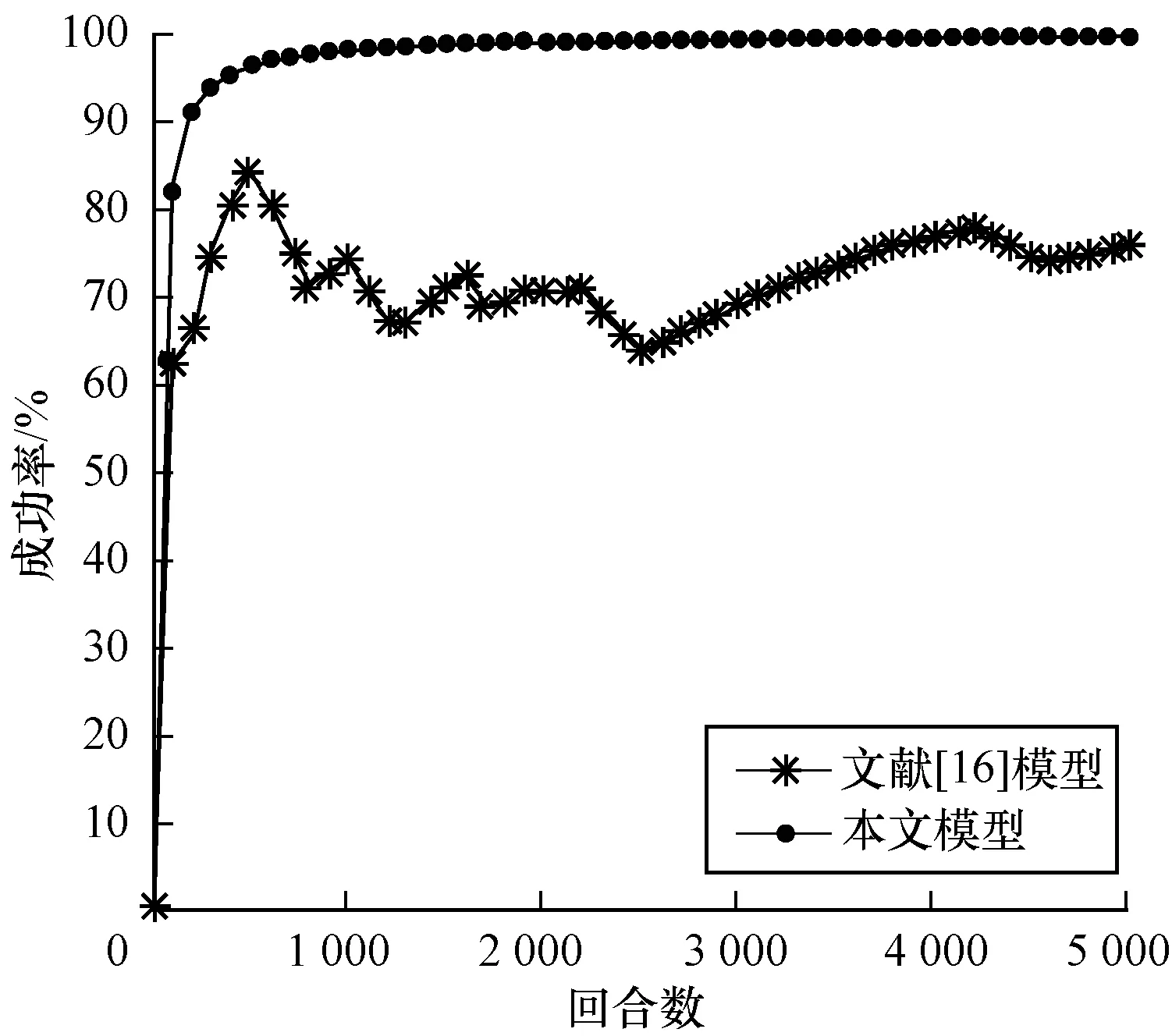
图9 环境车匀加速行驶时的汇入成功率对比

Fig.9 Merging success rate comparison of main-road vehicles with uniform acceleration

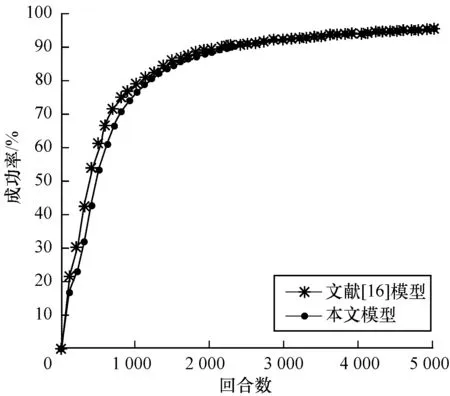
图10 环境车匀减速行驶时的汇入成功率对比

Fig.10 Merging success rate comparison of main-road vehicles with uniform deceleration

3种环境车速下最终完成训练时的汇入成功率如表4所示。从中可以看出,DDPG汇入车流模型在3种行驶情况下可以以较高的成功率汇入车流。训练完成时,成功率都能达到95%以上,说明该模型收敛速度快且稳定。在环境车匀速行驶、加速行驶中汇入成功率分别为97.42%和99.64%,分别超出DQN汇入模型成功率15.5%和23.68%;在环境车减速行驶中汇入成功率为95.34%,超出DQN汇入模型成功率1.02%。

表4 完成训练时的汇入成功率对比

Table 4 Merging success rate comparison at the end of training%

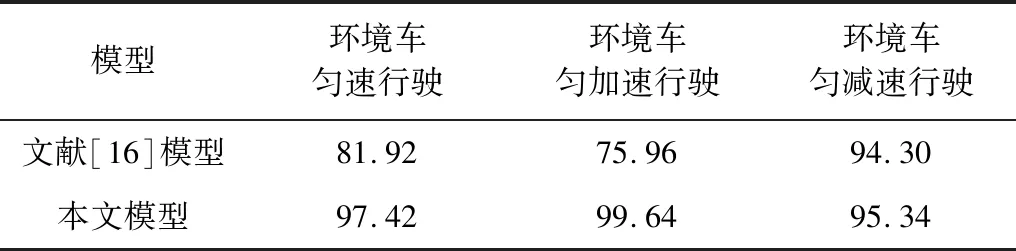
模型环境车匀速行驶环境车匀加速行驶环境车匀减速行驶文献[16]模型81.9275.9694.30本文模型97.4299.6495.34

4 结束语

本文构建基于连续动作空间DDPG算法的智能车汇流模型,并将其与基于离散空间DQN的模型进行对比。仿真结果表明,该模型的汇入成功率较高。DDPG易于收敛,学习效果稳定,能够提高智能车在汇入过程中的智能化水平,相比于离散动作空间的DQN算法更适合智能车汇入场景的应用。下一步将优化本文模型,使其具有较强的泛化能力并且适用于多车复杂环境。