基于时空相关性的短时交通流量预测方法

闫 杨,孙丽珺,朱兰婷

(青岛科技大学 信息科学技术学院,山东 青岛 266061)

0 概述

随着城市交通系统的快速发展,移动互联、车路协同、主动安全、自主高效的新一代合作智能交通系统已经成为未来道路交通管理系统的主要推动者[1]。作为新一代智能交通系统的重要一环,准确、快速的短时交通流量预测不仅可以帮助人们规划出行路线、节省出行时间,从而减少交通拥堵以及不必要的资源浪费,而且也为将来信息感知、深度互联、协同共享、智能处理、应用开放的智慧城市建设发挥至关重要的作用。

到目前为止,学者们已经提出了许多不同的短时交通流量预测方法,主要有基于时间序列的交通流量预测方法、基于统计概率的短时交通流量预测方法和基于机器学习的短时交通流量预测方法等三大类。

第一类为基于时间序列的交通流量预测方法。文献[2]提出一种基于季节性差分整合移动平均自回归模型(ARIMA)的短时交通流量预测方法,该方法针对不同的季节来对交通流量进行预测。然而由于交通流是随机和非线性的,而ARIMA方法主要处理线性关系,导致了单一的ARIMA模型无法分析非线性的交通流数据。文献[3]提出一种具有广义自回归条件异方差性(ARIMA-GARCH)的方法来预测交通流量,该方法将线性的ARIMA模型和非线性的GARCH模型相结合,以此来捕获交通流序列的条件均值和条件异方差,从而进行交通流量的预测。文献[4]提出一种基于时间序列分割与极限学习机相结合的交通流量预测算法,该算法预测速度快并且准确性高。

第二类为基于统计概率的短时交通流量预测方法。文献[5]提出一种四阶高斯过程动态模型(GPDM),四阶GPDM中的潜变量是四阶马尔科夫高斯过程,并且加权K最近邻(K-NN)算法被结合到模型中以对潜变量进行有效预测,然后通过GPDM和K-NN预测结果的平均值来估计未来交通流量。文献[6]提出一种利用线性条件高斯贝叶斯网络模型的方法来综合考虑交通流量的时间、空间维度以及交通流量的速度信息,从而进行短时交通流量预测。

第三类为基于机器学习的短时交通流量预测方法。文献[7]提出一种基于支持向量机(SVM)的精确多步交通流量预测方法,与传统的单步预测方法相比[8],该方法能够对未来某一时期的交通状态趋势进行精确预测。文献[9]提出一种基于时空自适应的多核支持向量机(AMSVM-STC)的预测方法,该方法将高斯核和多项式核杂交成AMSVM,利用粒子群优化算法对参数进行优化,从而能够根据实时交通流量变化趋势自适应地调整混合核权重,达到精准预测短时交通流量的效果。文献[10]提出一种基于堆栈自编码器(SAE)的预测方法,该方法使用贪婪的分层无监督学习算法进行逐层训练,从而使预测结果更加快速和准确。

近年来,深度学习的迅速发展为短时交通流量预测提供了更加多样化的方法。文献[11]提出一种基于长短期记忆网络(LSTM)的预测方法,该方法利用LSTM捕获时间序列数据中的长期依赖性的固有特征,使其能够对非线性的交通流量做出合适的预测结果。文献[12]提出一种DeepTrend模型,该模型由可以提取交通流时变趋势的提取层和使用LSTM网络能够对时变趋势进行计算和输出的预测层组成,该方法与单一的LSTM模型相比,能够更加准确地预测短时交通流量数据。文献[13]提出一种基于残差长短期记忆网络的交通流量预测方法,利用集成学习思想将空间分布的数据端到端训练到残差LSTM网络中,同时在每个LSTM单元后引入维度单元,显示建模特征维度之间的相互依赖关系。文献[14]提出一种基于门控循环单元(GRU)的预测方法,该方法所使用的模型少一个门控,因此,相比LSTM更加简单[15],运算速度也更快,并且考虑天气因素的影响,提高了预测精度。然而,由于LSTM和GRU模型只能处理时间序列,仅使用LSTM或GRU模型并不能全面分析交通流量的时间和空间特征,因此其交通流量的预测精度较低。

文献[16]提出一种基于深度学习的多组件时空图卷积网络(MCSTGCN),通过3个组件分别建模流量数据的近期、日周期、周周期特性,有效捕捉交通流量数据的时空相关性。文献[17]提出一种基于卷积神经网络(CNN)和长短期记忆网络(LSTM)相结合的短时交通流量预测方法(CNN-LSTM),该方法利用LSTM提取交通流量的时间特征和周期性特征,使用CNN提取交通流量的空间特征,最后将三者的特征进行融合,得到交通流量预测结果。然而,这种方法的缺点是将LSTM和CNN模块以并行的方式进行特征提取,导致最后得到的交通流特征并不能充分融合。文献[18]提出一种卷积-长短期记忆网络(Conv-LSTM)的方法,该方法将卷积神经网络和长短期记忆网络集成到一个模型中,并且使用双向LSTM(Bi-LSTM)模型来提取交通流的周期性特征,最后将特征进行充分融合,提高交通流量预测的准确性。文献[19-20]利用深度信念网络(DBN)来进行短期交通流量的预测,取得了较好的效果。

为预测短时交通流量,本文提出一种基于时空相关性的方法Conv-GRU。通过使用卷积-门控循环单元提取交通流量的空间和时间特征,并运用双向门控循环单元(Bi-GRU)得到交通流的周期性特征,对时空特征和周期性特征进行融合来预测交通流量。

1 系统模型

1.1 数据公式化

由于交通流量数据的预测点不均匀地分布在不同的区域或者路口,收集的交通数据的位置呈现不对称状态,并且间隔很大。本文将交通流量数据映射到一维矩阵,将预测点的流量数据放入矩阵的中心,并且根据距离预测点的远近,将其他点的交通流量数据填充到交通流量矩阵中。系统模型用于分析矩阵以找出预测点与其他点之间的空间相关性。一维空间信息矩阵表示为:

Ft=(F1,F2,…,Fr,…)

(1)

其中,t代表某一时刻,r代表某一区域或者路口,Ft代表t时刻所有区域的交通流量。不同时刻的一维空间信息矩阵为:

(2)

带有周期性的交通数据可以表示为:

(3)

(4)

1.2 本文系统模型

在进行数据公式化后,将上述数据矩阵输入到本文所构建的系统模型中。本文系统模型主要包括2个部分,第1个部分是卷积-门控循环单元(Conv-GRU)模块,第2个部分是双向门控循环单元(Bi-GRU)模块。使用Conv-GRU来提取交通流量数据的时空特征,并运用Bi-GRU来提取周期性特征,最后集中时空特征和周期特征来预测交通流量,总体模型框架如图1所示。

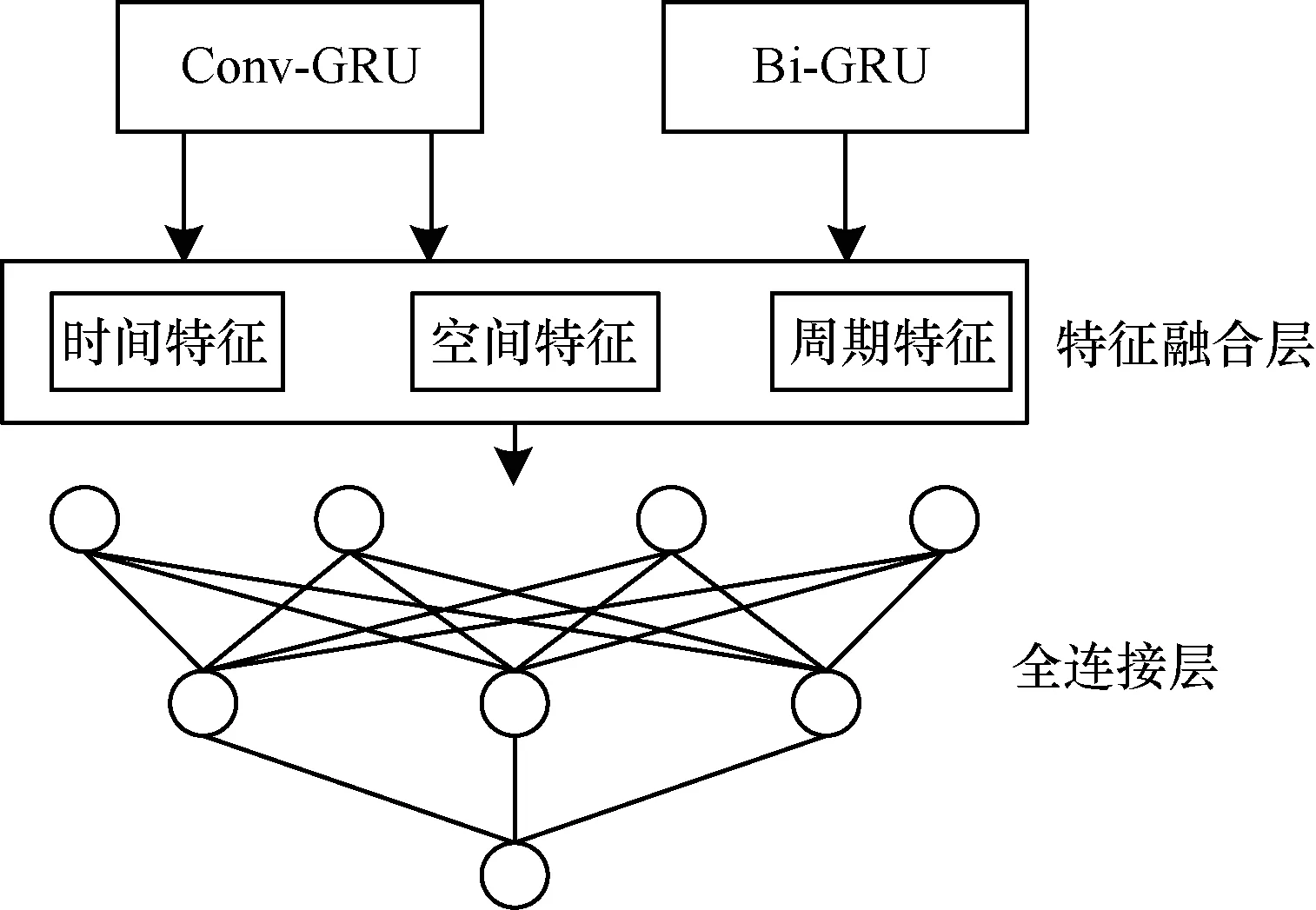
图1 系统总体框架

1.2.1 卷积-循环门控单元模块

卷积-门控循环单元(Conv-GRU)模块的输入矩阵可以表示为时间序列Fr=(F1,F2,…,Ft,…),其模块结构如图2所示。矩阵中的每行元素表示同一时刻要预测的点的相邻区域中其他交通流量值,即Ft=(F1,F2,…,Fr,…)。

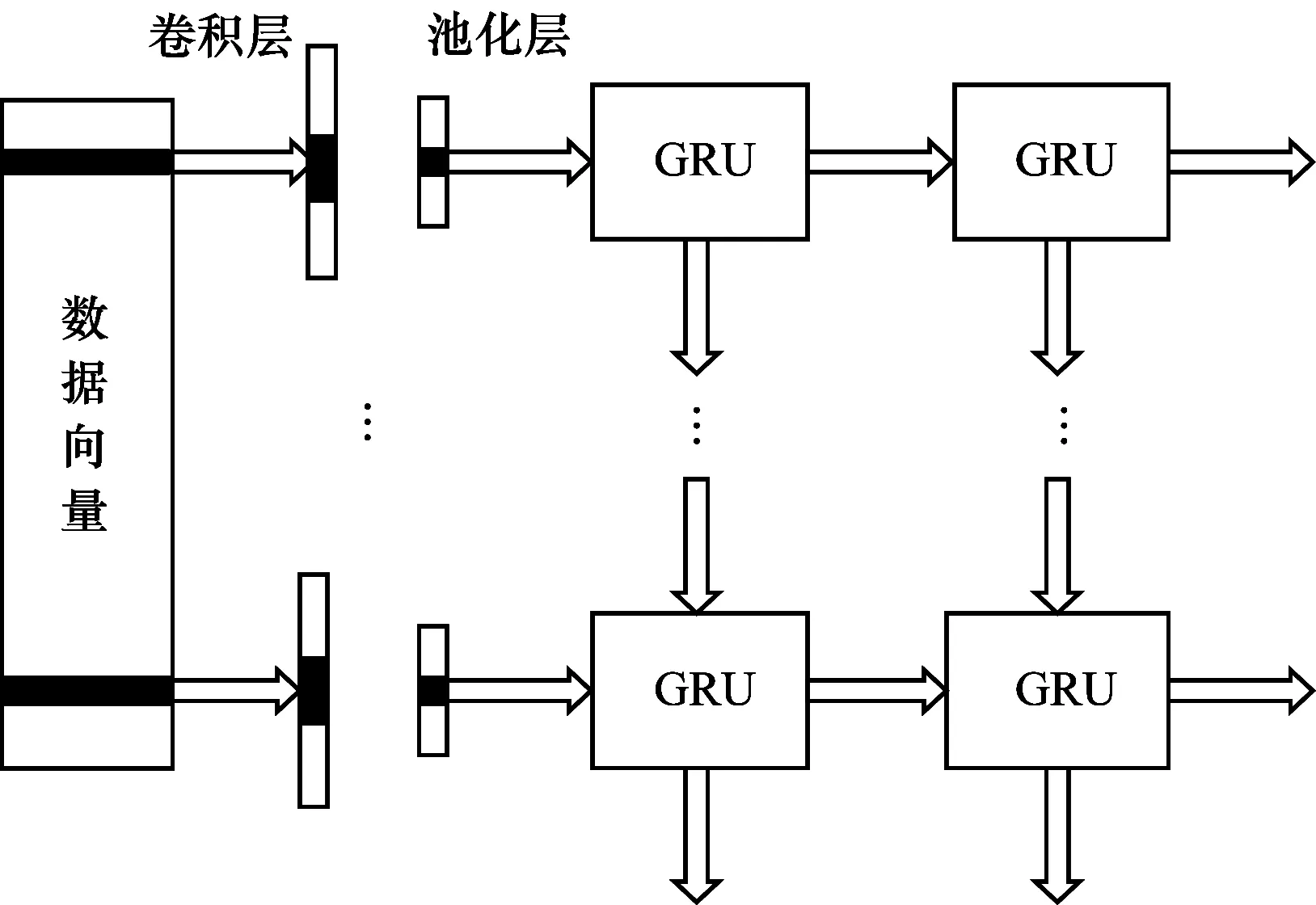
图2 Conv-GRU模块结构

交通流量预测具体步骤如下:

步骤1使用一维卷积来处理Ft中的每个元素。

通过滑动滤波器在数据矩阵中进行滑动卷积以获取局部感知域的卷积信息,本文中使用滤波器的卷积核为3,滑动步数为1。一维卷积图如图3所示。

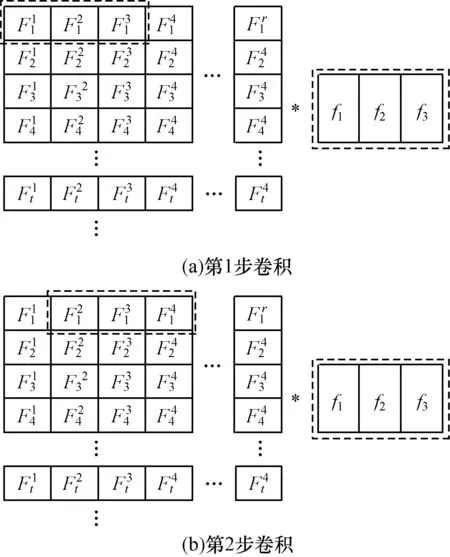
图3 一维卷积示意图

(5)

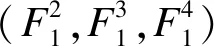
(6)

以此类推,最终得到整个交通流量数据的卷积值A=(A1,A2,A3,…)。

步骤2聚合所有的卷积值,以形成交通流量数据空间特征。

g(i)=R(Aiw+B)

(7)

φ(x)=max(0,x)

(8)

步骤3使用平均池化技术将卷积层中获取的空间特征进行合并缩小。

通过平均池化技术,使得合并后的维度大幅降低,这样可以过滤掉一些不必要的信息以获得更抽象的空间特征,平均池化如图4所示。

图4 平均池化示意图

空间特征矩阵中每一行代表的是一个时间段,因此第1个时间段池化后的特征为:

(9)

同理,第2个时间段池化后的特征为:

(10)

以此类推,可得第t个时间段池化后的特征为:

最早实行导师制的是英国牛津大学，时间可以追溯到14世纪，几百年来，牛津大学通过实行导师制培养出许多诺贝尔奖获得者，同时英国历史上的多名首相也毕业于牛津大学[2]。随后，本科生导师制开始在世界各大高校中逐渐应用。在我国高校中，本科生导师制起步较晚，最早是在1938年浙江大学实行。新中国成立之后，由于政治原因，本科生导师制被逐渐放弃，被苏联教育模式的学年制慢慢取代，并且一直沿用到今天。

(11)

其中,m、n以及p都为正整数,且p>n>m。

步骤4将卷积和池化后的空间特征输入到GRU模块中,以形成交通流量的时空相关性。在卷积及池化处理交通流量数据之后,输出的结果变为带有空间特征的时间序列矩阵C=(C1,C2,…,Ct,…),然后把C作为门控循环单元(GRU)模块的输入。

如图5所示,GRU模块结构包括更新门和重置门2个门控。更新门主要用来控制前一时刻的状态信息被带入到当前状态中的程度,更新门的值越大说明前一时刻的状态信息带入越多。重置门用于控制忽略前一时刻的状态信息的程度,重置门的值越小说明忽略状态信息越多。

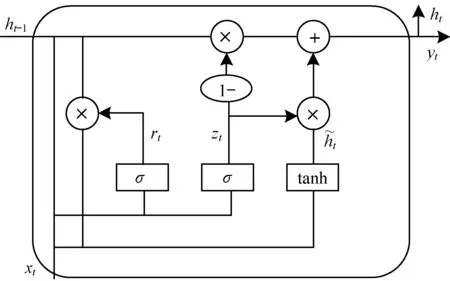
图5 GRU模块结构示意图

GRU模块结构具体方法如下:

1)将前一时刻的状态信息ht-1和当前时刻的输入xt送到重置门中,以确定前一时刻丢弃哪部分信息:

rt=σ(Wr·[ht-1,xt]+br)

(12)

其中,rt是重置门的输出,Wr是重置门的权重,br是重置门的偏置项。

2)将ht-1和xt送到更新门中,以确定要更新前一时刻的哪部分信息:

zt=σ(Wz·[ht-1,xt]+bz)

(13)

其中,zt是更新门的输出,Wz是更新门的权重,bz是更新门的偏置项。

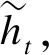
(14)

其中,Wh和bh是中间状态的权重和偏置项。

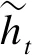
(15)

5)通过sigmoid函数将ht激活,得到融合空间相关性的时间特征序列。

yt=σ(Wo·ht)

(16)

(17)

其中,σ是激活函数。

1.2.2 双向循环门控单元模块

交通流量具有非常明显的周期特点,本文运用双向门控循环单元(Bi-GRU)来提取交通流量的周期性特征,由于Bi-GRU需要预测数据之前和之后的信息来提高预测的准确度,而本文只能使用预测时间之前的交通流量,因此选择预测点昨天的同一时间点以及预测点上个周同一时间点的交通流量数据作为模块的输入,以此来提取周期性特征。Bi-GRU模块如图6所示。

图6 Bi-GRU模块结构示意图

Bi-GRU模型分别由向上和向下堆叠的单向GRU模型组成(其原理和单向GRU模型相同),因此,双向GRU模型需要2个时间序列输入,最终输出结果(交通流量的周期性特征)由正向和反向2个输出共同决定。

1.3 损失函数

使用上述模型分别提取时空特征和周期性特征,将所有特征顺序连接到特征矩阵中,然后添加到全连接层进行预测,本文在预测时使用均方误差(Mean Squared Error,MSE)作为损失函数来进行训练,可以准确地描述真实值和预测值之间的差异:

(18)

其中,Fpredcit为短期交通流量的预测值,Ftrue为交通流量的真实值。本文使用RMSP(Root Mean Square Prop)优化算法来优化深度神经网络。RMSP优化算法通过设定一个超参数,可以自适应地调整学习速率,从而防止损失函数在更新时存在摆动幅度较大的情况,并且进一步加快了函数的收敛速度。

2 实验结果与分析

2.1 数据来源与实验环境

本文提出一种基于时空相关性的短时交通流量预测的方法。通过使用加利福尼亚运输性能测量系统(PeMS)的高速公路数据集来对Conv-GRU方法进行训练和评价。PeMS中使用的检测器每5 min收集一次流量数据,该数据集一共包含33个交通站点信息,每一个不同的站点都收录了从2017年1月1日—7月15日的交通流量数据。本文使用2017年4月10日—4月13日的数据进行分析,通过对该数据集的分析,发现交通流量数据呈现出很明显的周期性特征,如图7所示。

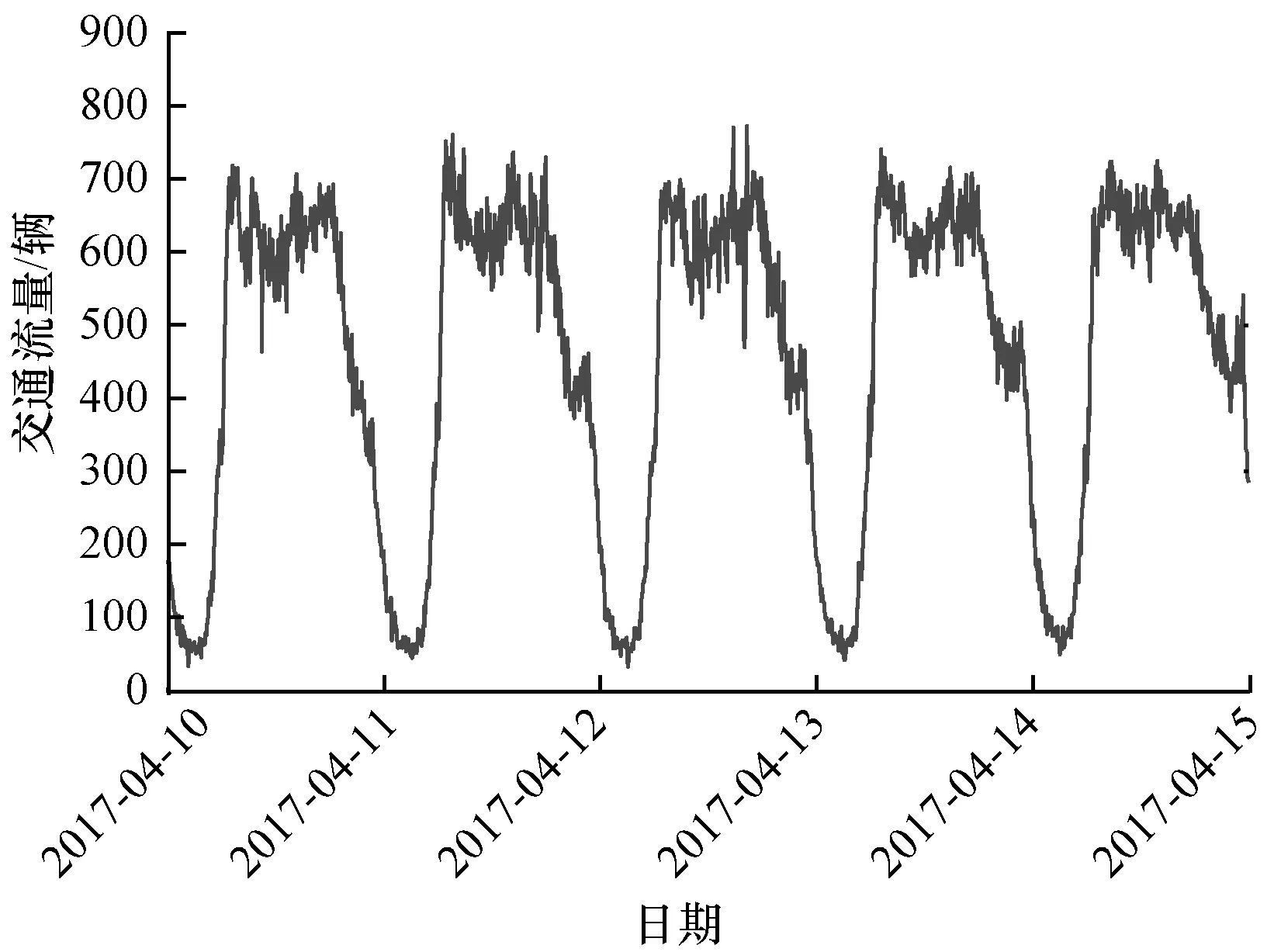
图7 交通流的周期性特征

本文所使用的软硬件平台如下:

硬件环境平台:Intel(R) Xeon(R) CPU E5-2650 v4 @ 2.20 GHz,250 GB内存,1 000 GB硬盘,Ubuntu 16.04.5操作系统。

软件环境平台:Python3.5,Keras,Tensorflow,scikit-learn等。

2.2 结果分析与评价

为证明本文方法的准确性,使用平均绝对误差(MAE)和均方根误差(RMSE)2个评价指标来评估预测结果,MAE能更好地反映出预测值误差的实际情况,RMSE是均方误差的算术平方根,RMSE的值越小,说明预测模型描述实验数据具有更好的精确度。两者计算公式如下:

(19)

(20)

其中,Fpredict是交通流量的预测值,Ftrue是交通流量的真实值。

为测试Conv-GRU方法的性能,使用6种不同的方法进行对比,分别是Conv-LSTM、CNN-GRU、CNN-LSTM、GRU、LSTM以及SAE。如表1、表2所示,Conv-GRU方法在MAE和RMSE上要低于CNN-LSTM、CNN-GRU、GRU、LSTM以及SAE,和Conv-LSTM基本相差不多。

表1 不同方法在工作日交通流量预测中的性能

Table 1 Performance of different methods in weekday traffic flow prediction

方法MAERMSE本文方法19.873 41028.447 581Conv-LSTM方法21.382 76929.882 264CNN-GRU方法23.579 84132.834 440CNN-LSTM方法22.038 42231.421 413GRU方法27.255 19838.443 176LSTM方法33.975 15744.918 871SAE方法27.681 10927.681 109

表2 不同方法在周末交通流量预测中的性能

Table 2 Performance of different methods in weekday traffic flow prediction

方法MAERMSE本文方法20.530 44728.897 232Conv-LSTM方法19.879 53528.263 375CNN-GRU方法23.659 01633.573 994CNN-LSTM方法21.100 65930.015 815GRU方法26.246 00337.976 083LSTM方法24.845 77835.931 767SAE方法26.770 52337.994 996

为更加直观地比较预测结果的准确性,本文使用CNN-LSTM、LSTM以及SAE 3种方法来与Conv-GRU方法进行对比,预测时间分别是工作日以及周末的上午8:00—12:00,预测结果如图8所示。

图8 4种方法工作日和周末预测结果

Fig.8 Working day and weekend forecast and results of 4 method

通过分析可以看出,无论是在预测工作日还是周末交通流量上,Conv-GRU方法的预测结果要比CNN-LSTM、LSTM以及SAE方法更加精确,这是因为Conv-GRU方法是将卷积神经网络和门控循环单元集成到一个模块,可以充分提取到短期交通流量数据的时间和空间特征,而CNN-LSTM方法[18]是将卷积神经网络和长短期记忆网络组合到2个并行的模块,分别提取交通流量的时间和空间特征,这样的预测方法不能够使交通流量的时间和空间特征完全融合,而且Conv-GRU方法使用Bi-GRU模块来提取周期性特征,这样就使得Conv-GRU方法比CNN-LSTM的方法在预测结果上更精确。

LSTM模型只是适合提取时间序列特征,并不适合处理空间特征,而Conv-GRU方法可以处理时间特征、空间特征以及周期性特征,因此预测的结果优于仅使用LSTM模型的预测方法。

在上述的方法中,由于堆栈自编码器(SAE)在进行训练时使用的是分层无监督学习算法,因此它并不能做到对交通特征的全局优化,并且其每一层的训练方法都是相同的,这就导致了SAE在训练多个神经层以后会出现多层递增式失效,即其性能会随着训练层数的增加而迅速降低,因此,堆栈自编码器的预测精度较差。

由图9、表1和表2数据可以看出,Conv-GRU方法和Conv-LSTM方法[19]之间无论是在预测性能还是预测结果方面都相差不大,但是在两者性能和预测结果相差无几的情况下,Conv-GRU方法每次迭代所需要的时间要比Conv-LSTM少,这主要是由于GRU模型与LSTM模型相比,少了一个门控单元,这就意味着GRU模型比LSTM少了几个向量乘法操作,而这在训练数据量特别大或者迭代步数特别多的情况下GRU要比LSTM节省很多时间,Conv-GRU方法和Conv-LSTM不同的迭代次数下的训练时间如图10所示。

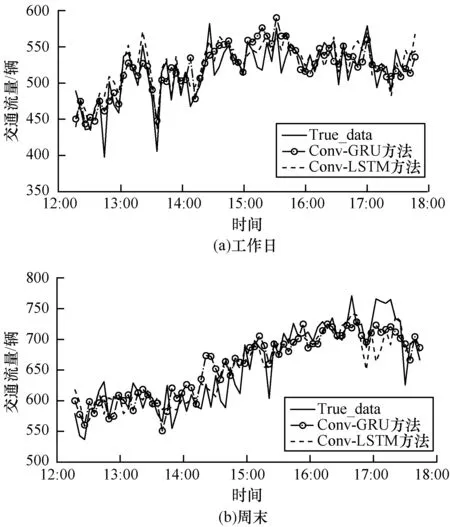
图9 Conv-GRU和Conv-LSTM工作日和周末预测结果

Fig.9 Conv-GRU and Conv-LSTM weekday and weekend forecast results

图10 不同迭代次数下Conv-GRU和Conv-LSTM的运行时间

Fig.10Running time of Conv-GRU and Conv-LSTM under asynchronous number

3 结束语

本文提出一种结合Conv-GRU和Bi-GRU的短时交通流量预测方法,该方法将流量数据映射到一维矩阵中,使用Conv-GRU方法提取交通流的时空特征,并运用Bi-GRU方法得到交通流的周期性特征。实验结果表明,与现有方法相比,该方法能够融合交通流的时空特征和周期性特征,并且和Conv-LSTM方法相比,收敛速度更快,能够适应交通流量迅速变化的特点。然而,本文方法也有很多不足,如没有考虑天气、节假日、社交活动、自然灾害等特殊情况,如何将上述信息加以利用,形成更加完善的短时交通流量预测方法是下一步需要解决的问题。