回归法在实时混合模拟数值子结构不确定性分析中的应用
2020-01-16徐伟杰陈梦晖王燕华
徐伟杰 陈 城 陈梦晖 郭 彤 黄 亮 王燕华
(1东南大学混凝土与预应力混凝土结构教育部重点实验室, 南京 210096)(2山东大学土建与水利学院, 济南 250061)
实时混合模拟试验是一种新型的抗震试验方法[1],它将试验结构分为试验子结构和数值子结构2部分,前者在实验室进行实时试验,易于模拟的部分作为数值子结构在计算机进行数值计算.与传统试验方法相比,该方法可以在足尺条件下对结构进行实时加载,能够全面反映结构的动力特性[2-5].然而,由于子结构的引入,实时混合模拟的试验结果受到多种不确定性的影响,主要包括数值子结构模型的不确定性和作动器动力特性不确定性.时滞补偿方法可以减小但不能完全消除试验中的不确定性,这些不确定性会导致实时混合模拟成为一个随机过程,使试验结果的可靠性降低,导致实时混合模拟试验无法大规模推广.为了解决不确定性对试验结果的影响,Abbiati等[6]将多项式混沌展开(PCE)引入混合试验,证明通过若干组重复试验可以对试验结果进行不确定分析.Chen等[7]进一步将PCE引入线性结构的实时混合模拟试验中,证明回归法可以有效计算PCE系数,研究不同时滞下数值子结构不确定性与试验结果的关系.然而,针对于非线性结构的不确定性研究较少,PCE在实时混合模拟试验中的模型效果也没有评价标准.
本文将模型误差作为评价PCE模型效果的评价指标,通过非线性结构的数值模拟,研究回归法在实时混合模拟数值子结构多项式混沌展开不确定性分析中的应用.
1 多项式混沌展开
求解不确定性问题的方法可以分为统计方法和非统计方法.蒙特卡罗模拟(MC)对随机过程进行大量采样,得到该随机过程响应的频率或者平均值,然而该方法收敛速度较慢,需要进行大量的抽样才能达到准确效果[8].非统计方法将不确定过程在不确定空间进行离散化,代表性方法有PCE[9-11].该方法将不确定性模型的输出映射到一系列正交随机多项式上,从而达到指数收敛速度.
Winer-Hermite多项式将不确定性模型的输出映射到Hermite多项式上.令X(ω)为一个由服从高斯分布的不确定性参数ξ={ξi1,ξi2,…ξin,…}构成的随机过程,则[10]
(1)
式中,a0,ai1,ai1,i2为PCE系数;Hn为n阶Hermite多项式.在PCE中,X(ω)的均值等于a0,X(ω)的方差等于除a0外PCE系数的平方和.
当不确定性参数不满足高斯分布时,式(1)的收敛速度并不快.广义混沌多项式利用Askey多项式将Winer-Hermite多项式扩展到其他分布[11].与Winer-Hermite多项式类似,广义多项式混沌可将随机过程X(ω)表示为
(2)
式中,In为n阶Askey多项式.
2 多项式系数计算方法
多项式系数ai的计算是PCE的关键.多项式混沌在实际应用中只能为有限项的多项式,故需将式(1)截断为
(3)
式中
Hi{ξ}T={H0,H1(ξ),…,Hi(ξ)}T
式中,P为混沌多项式的项数,且
(4)
式中,p和M分别为多项式的阶数和不确定性变量的个数.根据是否将原模型映射到正交空间重新构建控制方程,计算系数的方法可分为侵入式算法和非侵入式算法2种.侵入式算法基于Galerkin映射;非侵入式算法则包括回归法和非侵入式映射法.与侵入式算法相比,非侵入式方法计算简便,实际工程中应用更为广泛.
2.1 Galerkin映射法
令εL为截断后的多项式混沌和不确定性模型之间的误差,则[9]
(5)
利用多项式之间的正交性,该误差在各阶多项式构成的子空间为0,可以构成P+1个耦合方程,从而计算多项式混沌的系数ai.
2.2 回归法
回归法对模型真实解与多项式混沌基进行回归分析,计算多项式混沌的系数[12].该方法通过对样本点取样,不需要对正交基进行映射,即
ai=minE(X′(ω)-X(ω))d
(6)
式中,minE为期望的最小值;X′(ω)为样本点处模型真实解;d为回归的阶数,通常取2.
文献[13]指出,当样本点数目大于P(M-1)时,回归效果并不会随点数增加而明显变化,因此回归点数一般取为P(M-1).采用回归法计算得到的多项式混沌与真实模型相比,样本点精确度较高,非样本点精确度较低.
2.3 非侵入式映射法
非侵入式映射法与Galerkin映射类似,都是将样本值映射到基函数中.然而,非侵入式映射法通过定义样本权重计算,将系数的计算转换为不同权重下样本点的积分,因此不需要重新构建控制方程[12].
2.4 非侵入式算法比较
UQlab是一个基于MATLAB的不确定性分析软件,该软件采用非侵入式算法计算多项式混沌的系数[13].UQlab采用最小角回归实现回归法参数计算.对于非侵入式映射法,通过高斯积分的权重选择样本点计算多项式的系数,样本点数为(p+1)M.显然,当随机变量维度较低时,非侵入式映射法效果较好,而当维度较高时,回归法效果较好.以3个随机变量为例,回归法和非侵入式映射法所需的样本点数见图1.由图可知,除一阶多项式外,非侵入式映射法需要的样本点数大于回归法,且阶数越多,相差越大.因此,回归法对处理高维问题要优于非侵入式映射法.
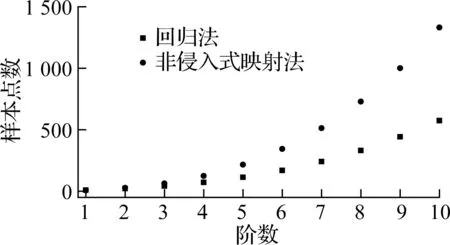
图1 回归法和非侵入式映射法所需的样本点数
3 模型误差
PCE的目的是建立原始模型的代替模型,其效果主要体现在代替模型与原始模型的接近程度上.对于回归法,模型精度在样本点处精度较高而在非样本点处精度较低,因此不能采用样本点效果来判断PCE效果.
建立PCE模型后,在样本空间随机抽取100个样本,计算PCE模型与原始模型的误差平均值M,即
(7)
式中,XORG和XPCE分别为原始模型和PCE模型的输出.分析过程中采用100个随机样本点,充分考虑了不确定性的影响,M直接反映了PCE模型与原始模型的误差,因此可以用于评价PCE的效果.然而,由于引入额外的样本计算,该方法更适合于模型运算量不大的情况.当模型运算量较大时,可以减少样本抽取点数,但不应小于10个样本,否则无法反映模型的真实效果.
4 数值模拟
4.1 数值模型
以单自由度非线性结构为例,研究回归法在实时混合模拟数值子结构多项式混沌展开不确定性分析中的应用.对于存在时滞τ的单自由度线性结构,其结构运动方程可以写为时滞微分方程的形式,即
(8)
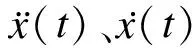
(9)
式(9)为式(8)的最不利形式,即阻尼全部集中于数值子结构而刚度全部集中于试验子结构.采用Bouc-Wen模型模拟结构的非线性,恢复力计算式为
re(t)=ηkx(t)+(1-η)kxyz(t)
(10)
式中,xy为数值子结构的屈服位移,此处取值为0.1 m;k为结构的线弹性刚度;η为数值子结构屈服前后的刚度比,此处取值为0.1;z(t)为Bouc-Wen参数,由下式计算得到:
(11)
式中,β、γ、q为控制滞回曲线形状的参数,此处分别取值为0.55、0.45和2.
结构位移的最大响应是结构分析的重要指标之一.当时滞微分方程的质量、阻尼和刚度均确定时,可计算求得结构位移响应最大值;反之,结构位移响应最大值则具有不确定性.传统的MC模拟需要进行大量运算,才能计算出位移响应最大值分布.若采用多项式混沌,将质量、阻尼和刚度作为PCE不确定性输入,位移最大值作为PCE输出,通过少量的数值模拟即可计算出位移响应最大值分布.
为不失一般性,假定时滞微分方程中的质量、阻尼和线弹性刚度为不确定性参数,且均服从高斯分布,均值分别为1 kg、0.251 3和39.478 4 kN/mm.不确定性参数均方差取如下的4种情况:① 均方差为均值的0.05倍,即均方差与均值的比值σ=0.05;② 均方差为均值的0.10倍,即σ=0.10;(3)均方差为均值的0.20倍,即σ=0.20;④ 均方差为0,即σ=0,说明位移最大值不存在不确定性,因此不需要对其建立PCE模型,其结果仅用于与其他情况进行对比.地震波输入采用MU2035,为保证结构进入非线性,其峰值加速度为2.468g.实时混合模拟的时滞τ取为0~10 ms,每个时滞情况下考虑3种不确定性参数均方差工况,因此需要构建33个PCE模型,PCE的阶数为7,采用稀疏取样方法取样,样本点数为240.采用最小角回归法方法,计算式(1)中的120个系数.
4.2 不同时滞下的PCE模型
采用UQlab计算PCE模型,采用回归法计算模型系数.对于7阶PCE模型,当不确定性变量数为3时,模型系数共120个.σ=0、0.05、0.10、0.20时位移最大值的均值与方差、时滞的关系曲线见图2.由图2(a)可知,时滞相同时,输入的不确定性越大,位移最大值的均值就越大.当时滞为0时,σ=0.05、0.10、0.20较σ=0时的位移最大值分别增加2.0%、6.0%、10.4%.当输入的不确定性不变时,时滞越大,位移最大值的均值越大,且这一规律随输入不确定性的增大而更加明显.当时滞为10 ms时,σ=0.05、0.10、0.20较σ=0时的位移最大值分别增加2.6%、7.6%、14.6%.由此可知,时滞越大或输入不确定性越强时,实时混合模拟试验越需要进行不确定性分析.
由图2(b)可知,时滞相同时,输入的不确定性越大,位移最大值的方差越大.对于σ=0.05、0.10两种情况,位移最大值的方差均随时滞增大而增大;而σ=0.20时位移最大值的方差和时滞之间并没有明显的关系.显然,σ=0.20的情况与σ=0.05、0.10的情况不符,需要通过误差平均值评价模型的准确性.
4.3 不同时滞下的PCE模型误差
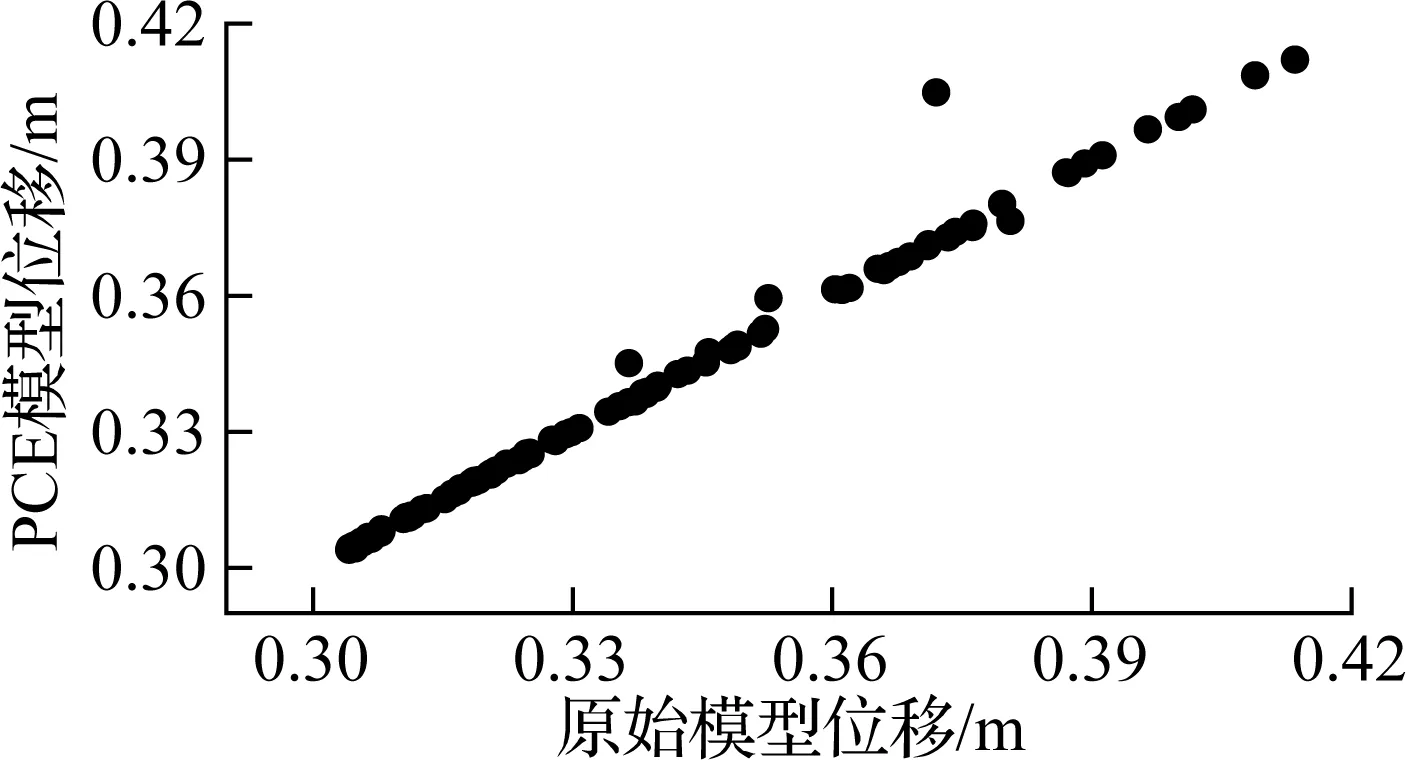
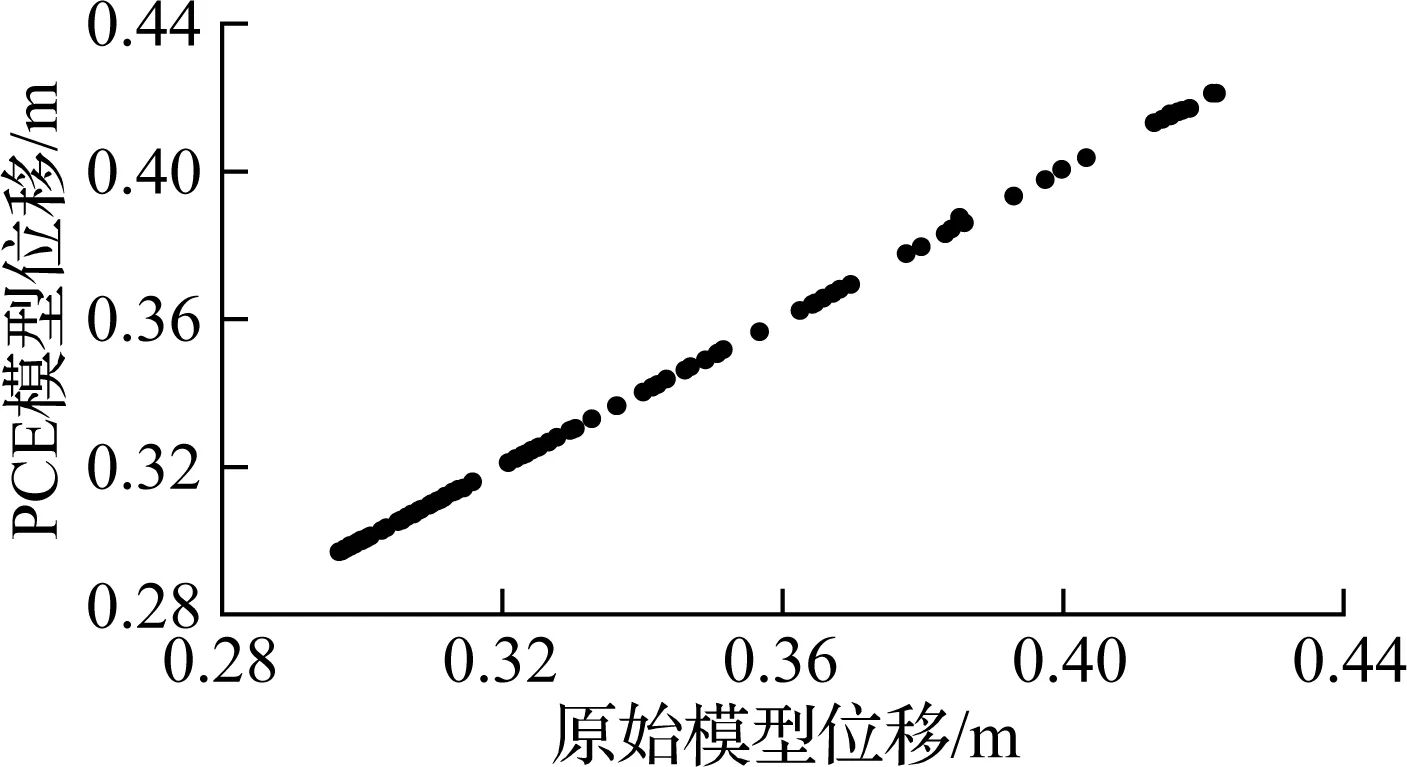
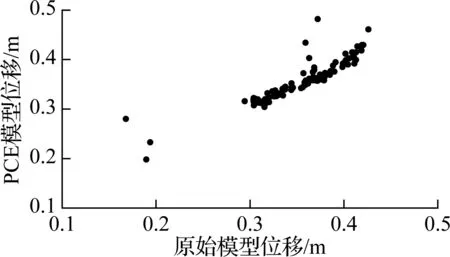
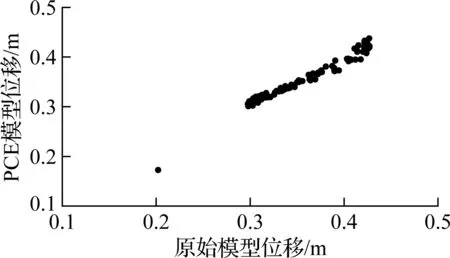
对上述33个模型采用误差平均值验证PCE模型的准确性.对于每个模型,在样本空间中任取100个样本,计算PCE与原始模型的误差.图3给出了时滞τ=5、10 ms时100个样本点的PCE模型和原始模型位移值.由图可知,随着不确定性参数均方差的增大,PCE模型和原始模型的误差也增大.根据式(7),不同PCE模型误差见表1.

表1 PCE的模型误差 %
由表1可知,当不确定性参数均方差为均值的0.05倍时,误差平均值的变化范围为0.002%~0.02%;当不确定性参数均方差为均值的0.10倍时,误差平均值的变化范围增大为0.02%~0.4%;当不确定性参数均方差为均值的0.20倍时,误差平均值的变化范围增大为0.5%~5%.显然,随着变量方差的增大,PCE模型的准确性明显下降.当不确定性参数均方差提高4倍时,位移最大值的模型误差增大了250倍.因此,图3(b)中位移最大值不随时滞增大而增大可以认为是由PCE模型误差导致.当不确定性参数均方差较小时,采用回归法计算的PCE模型仅需少量的样本点即可得到比较精确的结果;而当不确定性参数的方差较大时,采用回归法计算的PCE模型需要更高的阶数和更多的样本点才能保证准确性.
5 结论
1) 当数值子结构参数存在不确定性时,位移最大值的均值要比数值子结构参数取均值时的位移最大值大,且输入不确定性参数越大或时滞越大,位移最大值的均值和方差越大.
2) 多项式混沌展开效果可以采用模型误差评价.模型误差越小,说明多项式混沌展开越精确,对原模型的替代效果越好.
3) 在实时混合模拟试验中,当数值子结构不确定性参数均方差较小时,采用回归法计算的PCE模型仅需要少量的样本点即可得到比较精确的结果;而当不确定性参数的方差较大时,采用回归法计算的PCE模型需要更高的阶数和更多的样本点才能保证准确性.
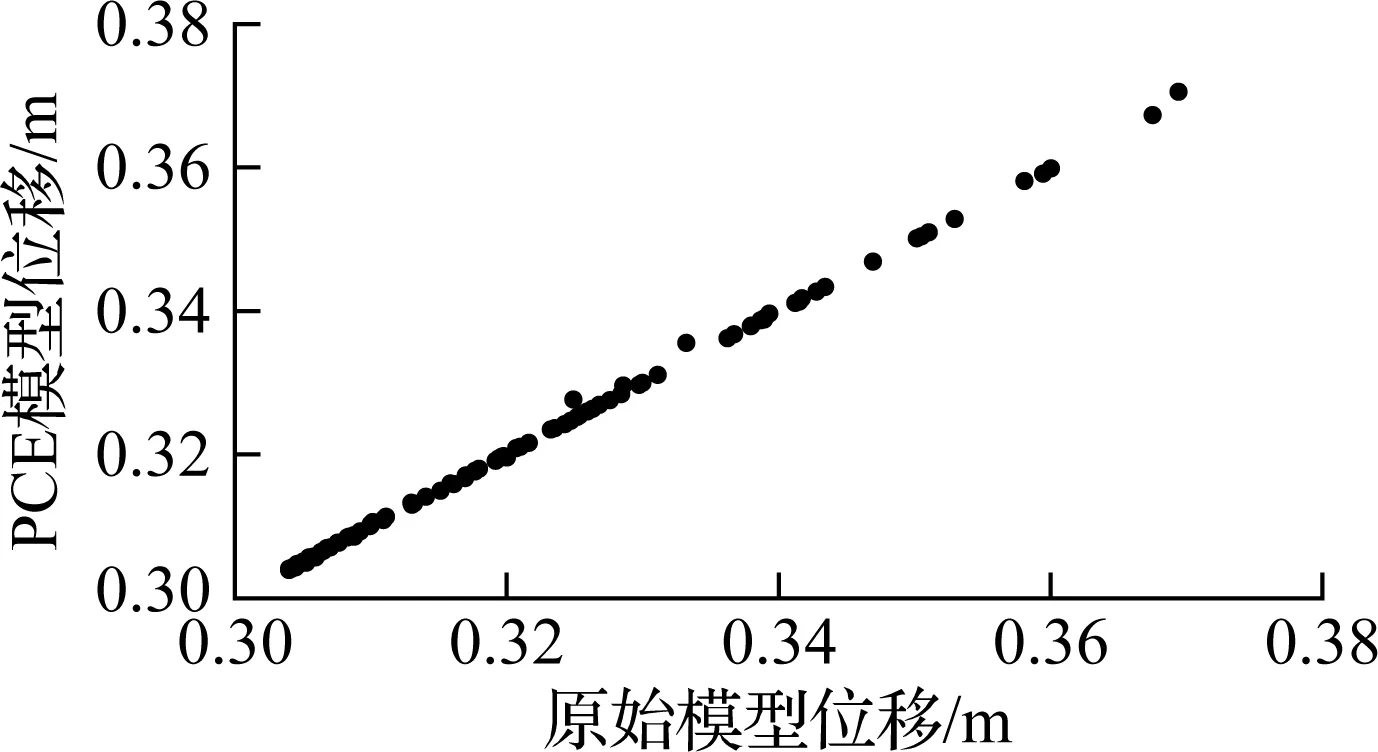
(a) τ=5 ms,σ=0.05
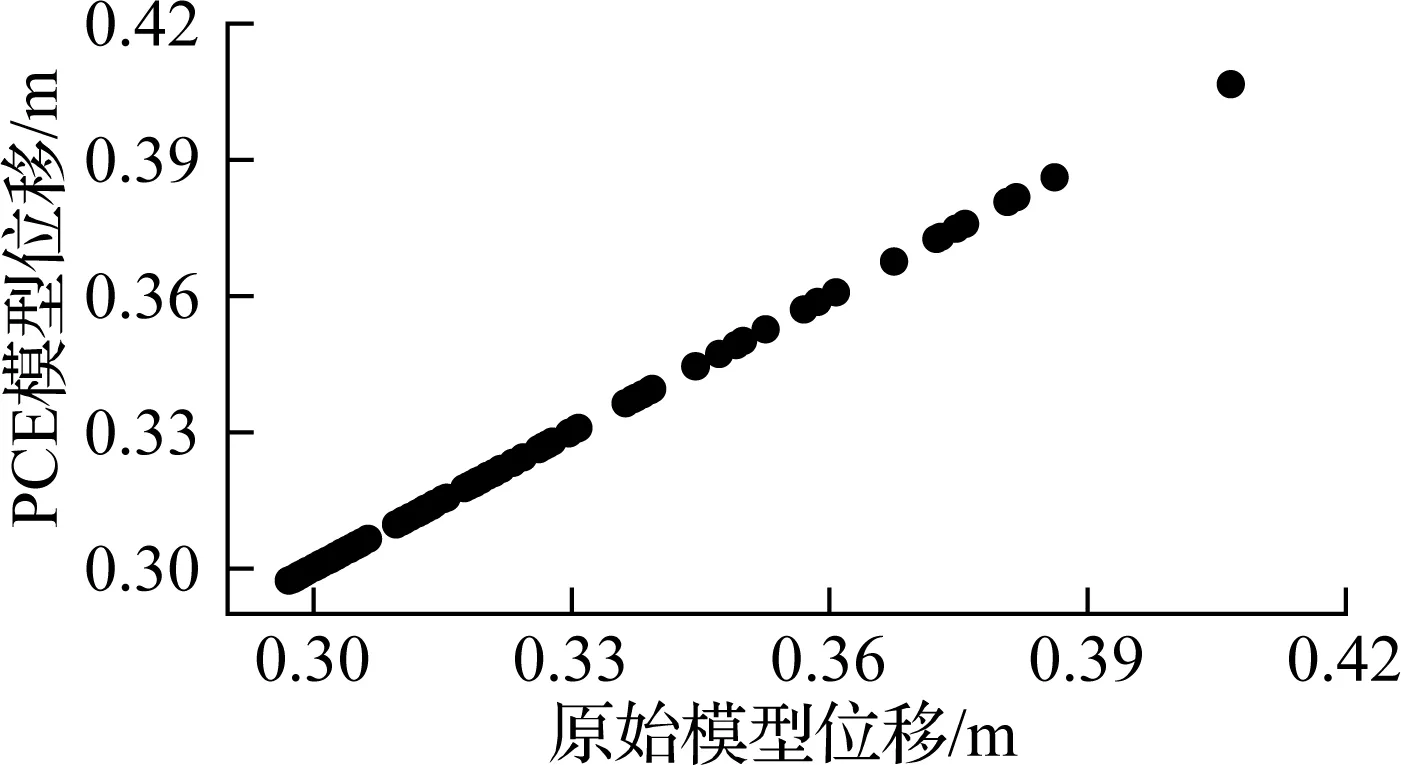
(b) τ=10 ms,σ=0.05
(c) τ=5 ms,σ=0.10
(d) τ=10 ms,σ=0.10
(e) τ=5 ms,σ=0.20
(f) τ=10 ms,σ=0.20
