基于GA-SVM的航材装备维修费用预测研究

刘 硕，崔崇立，程 鑫，赵 磊 LIU Shuo,CUI Chongli,CHENG Xin,ZHAO Lei

（1.空军勤务学院，江苏 徐州 221000；2.94862部队，上海 200082）

航材保障是航空兵装备工作的重要组成部分，航材保障工作质量直接决定着航空兵的作战能力，在现代化战争条件下，航材维修保障作为航材保障工作的重要环节是保证战机处于完好状态，时刻准备执行作战任务的重要前提，是夺取战争胜利的关键。

航材维修保障费用是航材全寿命周期费用的重要组成部分，通过对航材装备寿命周期费用的分析可知，航材保障工作中飞机的使用维修费通占寿命周期费用65%～80%，在航材装备寿命周期费用中居于主导地位[1]。因此，对航材保障维修费用进行预测能有效提高航材全寿命周期管理、决策支持航材保障费用规划、提升航材保障维修效能。当前航材保障面临着维修影响因素与费用之间非线性关系复杂，而解决处理难的问题。支持向量机作为非线性处理的有效工具，可以用于该类问题的解决。但支持向量机也存在自身不足，其在核函数的选取上缺乏明确的规则，核函数选取具有盲目性特点，同时参数的选取确定对结果的预测精度存在显著影响[2-4]。基于此笔者通过遗传算法优化支持向量机的参数，利用改进支持向量机，进行航材装备维修费用预测，有效提高了预测精度。

1 支持向量机

支持向量机（SVM）基于结构经验最小化的原则，建立具有良好映射能力和泛化能力的模型，支持向量机通过求解凸二次优化问题得到支持向量以保证全局的最优解[5-7]。

支持向量机的常用回归算法如下所示：

给定数据集H=｛（x,yi）|i=1,2,…,l｝，其中xi是输入变量，yi是输出变量，l是数据点的总数，对于线性回归，回归方程形式为：

对于常见的支持向量机的回归形式，其损失函数可表示为：

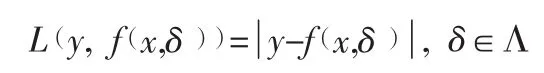
针对本文航材装备费用与其影响因素的不确定性，笔者采用一种新的损失函数构建回归支持向量机，此函数为ε不敏感损失函数，表示为：

式中：

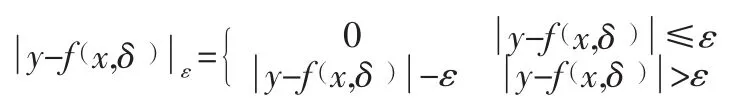
在这种损失函数中，如果预测值和实际值之间的差别小于等于ε，则损失等于0，预测值和实际值之间的差值大于ε，择取

使用ε不敏感损失函数构建支持向量机求解回归估计问题，是对如上所示的ε不敏感损失函数（ε≥ 0）进行风险最小化，下式的最小值即为问题的解。

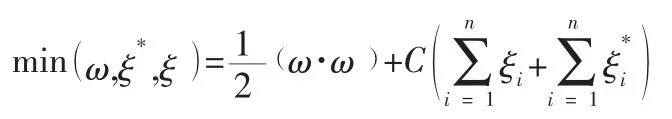
式中：

将式中的凸优化问题变为在二次规划优化中寻找向量ω的问题，即求解所求向量：

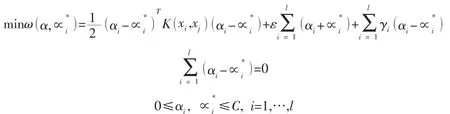
其中：K（xi,xj）=φ（xi）φ（xj）是支持向量机的核函数，以此核函数求解上述问题，得到支持向量机的回归函数为：函数[10]。基于此本文支持向量机核函数采取径向基函数进行问题求解。

2 构建GA-SVM航材维修费用预测模型

2.1 GA-SVM预测模型设计

航材装备维修费用模型是根据航材保障实际工作中产生的历史维修费用数据，利用遗传算法优化支持向量机方法进行训练，推测出航材维修费用规律，进而对未来航材保障工作进行规划预测[11]。基于遗传算法优化支持向量机的维修费用预测模型流程步骤如下（模型流程图如图1所示）：

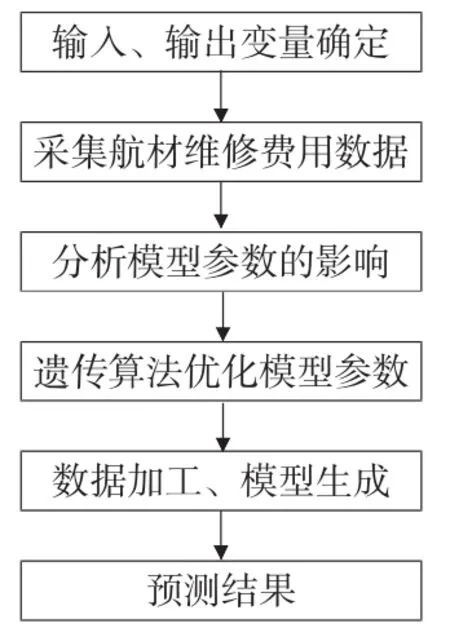
图1 预测模型步骤图

步骤1：航材维修费用预测模型变量的选择。模型输入向量和输出向量的选择建立在对航材维修费用的影响因素详细分析基础上。

步骤2：样本数据的选取。根据航材保障工作实际，合理采集不同机型的航材维修费用及相关影响因素数据，并将其分类为训练样本和测试样本。

步骤3：利用支持向量机训练模型。模型训练首先要对训练样本数据进行预处理，其次分析选定核函数的模型参数，最后利用遗传算法对模型参数进行寻优确定预测模型。

步骤4：检验预测模型。利用步骤2中的测试样本对确定的模型进行检验，证明模型的有效性，并将改进模型与其他模型方法进行对比。

步骤5：预测模型应用。将经过验证的预测模型应用于航材保障工作实践。

其中αi-∝非零所对应的样本即为支持向量，目前常用核函数种类繁多，包括线性核函数，二项式核函数，多项式核函数，多层感知高斯器核（MLP），径向基核函数（RBF），ERBF核函数等，结合不同函数的特点和具体问题灵活选取合适的核函数。通常来说径向基函数相比于线性函数预测精度更高，两者之间更倾向于选择径向基函数[8]；多层感知器核精确度不比径向基函数好，且其具有条件限制[9]；多项式核函数在叫阶次较高时数优化复杂，且耗费大量时间及资源，性能欠佳于径向基核

2.2 构建SVM训练样本集

支持向量机回归模型的构建要建立在训练样本数的基础之上，其表示为yi=f（ai,ai-1,…,ai-k），其中：xi=aiai-1,…,ai-k为输入矢量，yi=ai+1为输出值，k为输入矢量的维数。

2.3 遗传算法优化模型参数

遗传算法（GA）是借鉴生物进化过程而提出的一种人工智能算法，主要用于问题优化寻解。其基本思想是将问题的优化类比为生物的进化过程，通过生物界常见的染色体复制、交叉、突变等一系列过程产生所需问题的解，并以适应度作为决策条件，淘汰对环境适应度低的问题解，增加对环境适应度高的问题解，在N次的进化过程中，可能得到适应度很高的问题解。遗传算法的应用减少了陷入局部最优解的风险，具有良好的鲁棒性。

在支持向量机算法中为了使预测结果具有更高的精度，在进行样本训练之前需要对参数进行优化，由上述支持向量机算法原理可知，本文选取RBF作为核函数，则此时需要对惩罚因子C和RBF核参数γ做出寻优，基于此，笔者选择遗传算法对支持向量机参数进行优化，优化过程如图2所示。在利用支持向量机进行计算之前，通过遗传算法对参数进行优化处理，再用支持向量机对样本进行训练。

2.3.1 基因编码策略

支持向量机最佳参数选取过程是复杂的连续参数优化问题，常见的基因编码方式有浮点数编码、二进制编码等，笔者拟采用二进制编码方式对支持向量机的惩罚参数C和RBF核参数γ进行染色体基因编码，并随机产生一组参数染色体。

2.3.2 适应度函数

适应度函数的选择对遗传算法的收敛和支持向量机最优参数的选取产生直接影响。笔者选取9次交叉验证的实际值与预测值差值平方和作为适应度函数F：

式中：yi为第i次训练中的训练样本真实值，yˆi为第i次验证中通过支持向量机训练得到的预测值。

2.3.3 选择操作

选择操作是对个体的适应度函数评价后进行的操作，选择操作是为了保留优秀基因，保证算法的高效性同时可以维持染色体之间的合理差异，避免“早熟”现象产生。目前常用的选择操作有随机便利抽样、局部选择、比例选择、轮盘赌选择等，笔者采用轮盘赌法对父代染色体做出选择。

2.3.4 交叉操作

交叉操作是生物进化过程中的重要一环，其通过染色体交叉互换基因繁殖产生新后代，保证生物多样性。笔者拟采用单点交叉法对染色体间的基因进行交换，交叉率为0.8。

2.3.5 变异操作

遗传算法中的变异实质上是个体染色体自身的变化，其思想源于生物界中的物种变异，经过变异形成新的个体。笔者选择单点变异方法，变异率为0.01。

经过上述一系列操作得到新的染色体，使得初始确定的模型参数不断得到改进，最终当满足约束条件时，停止遗传算法的迭代操作得到目标函数的最优解译码，求得最优的惩罚因子C和核函数参数γ。

在此基础上将遗传算法优化与传统网格优化情况进行比对，其比对结果如图3所示。通过结果显示遗传算法收敛速度明显快于传统网格优化方法，收敛精度明显高于传统网格优化，遗传算法更加适用于参数优化。

图2GA-SVM优化流程图

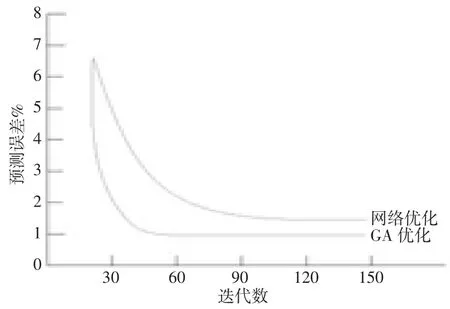
图3 GA与网格优化效果比较

3 实例分析

3.1 数据源和数据预处理

本研究的数据取自飞机保障实际过程中航材装备维修费用的历史数据，为了实现对模型的误差分析和预测检验，本文共采集了12组数据，其中选取前9组数据作为训练样本，后3组数据作为测试样本。其数据如表1所示，同时表1中各参量数据含义为：平均故障间隔时间MTBF；二次出动的准备时间SGR；单位飞行小时的维修时间DMMH；平均修复时间MTTR；发动机更换时间ERT；任务可靠度DR；航材备件利用率SPR；装备故障检测率FDR；装备故障隔离率FIR。

表1 航材维修费用表

由于各指标的衡量标准和维数存在差异，为了防止数据溢出，保证模型的精度，在训练模型前需对数据进行预处理，消除量纲并使数据具有可比性，本文采用最小最大化方法对数据进行处理，其表达式如下：

经过最小最大化方法处理之后，各指标数据映射到了0,［］1区间，并作为支持向量机的输入向量训练模型。

3.2 预测结果分析与对比

笔者选取RBF核函数为SVM模型的核函数，ε精度选取为0.001，通过遗传算法对惩罚因子C和核参数γ进行参数优化。遗传算法的参数设置为：交叉概率0.8，变异概率0.01，初始种群规模为20，进化代数为100，适应度函数为9次交叉验证的实际值与预测值差值平方和，各参数的搜索区间分别为C∈［1,5 00 0 ］，γ∈ ［0.0 1,150］，利用表1数据得到优化支持向量机参数为C=990.825，γ=1.8764。

利用优化参数的支持向量机、多元线性回归和BP神经网络分别训练数据样本并对测试样本进行预测，得到前9组数据的拟合数据以及后3组数据的预测值如图4所示，其中BP神经网络隐藏神经元个数为9个，隐含层传递函数为tansing函数，输出层以线性函数作为输出函数，允许精度为0.001，设置最大训练次数为2 000次，3种方法预测结果比对结果如表2和图5所示：

图4 实际值与预测结果对比图

图5 预测值误差对比图

表2 GA-SVM与多种模型比对表

经过对比发现利用遗传算法优化的支持向量机预测精度明显优于多元线性回归、BP神经网络等的预测结果，证明了GA-SVM算法的可行有效。

4 结论

笔者在支持向量机适合应用于小样本、高维、非线性数据预测的基础上，利用遗传算法对支持向量机中的径向基核函数相关参数进行优化，得到模型最优参数以保证维修费用预测的精度。通过实例验证了该模型改进效果显著，预测精度比BP神经网络、多元线性回归等的预测精度都要高出许多，说明运用GA-SVM进行建模分析是可行的，对快速准确预估航材维修费用具有重要意义。